生态-水网系统关键影响因子识别研究
李树文,龙亚会,马 宁,姜 琦,常向萍
(河北工程大学城市建设学院,河北邯郸056038)
层次分析法于20世纪70年代末由美国运筹学家Satty T.L.提出后,理论研究与应用都得到了快速的发展,衍生出改进层次分析法、模糊层次分析法、可拓层次分析法和灰色层次分析法等多种方法,应用于安全科学、环境科学等多种领域。近年来,为降低层次分析法中的主观影响,学者们将其与其它决策方法联合应用于多种领域,取得了很多的研究成果。如与灰关联理论,模糊数学等的联合使用。
生态—水网系统是一个多元素、多介质、多维数的开放性复合系统,其复杂性和多样性决定了指标选择和量化的困难性。为降低复合系统中指标设置的随意性和冗余性,提高复合系统耦合模拟、管理评价的高效性,本文选择了层次分析法和熵值法联合使用对生态-水网复合系统指标进行综合量化。
1 评价方法简介
对于复合系统的指标量化,选取合适的方法是十分关键的,方法不同有可能导致评价结果不同。因此,应以科学的方法对所选指标进行量化。量化的方法分为主观型和客观型两大类:主观型是根据决策者对各项指标的主观判断来赋权,如Delphi法、层次分析法等;客观型是依据客观信息进行赋权,如熵值法、CRITIC法等。本文采用主观和客观相结合的方式,也就是应用层次分析法和熵值法组合量化来评价复合系统的十项指标。
1.1 层次分析法
层次分析法(简称 AHP)是一种定量分析和定性分析相结合的无结构的多准则决策方法[1]。通过对复杂事物逐级分解简化后对事物进行综合分析。具体方法如下:
建立层次结构模型及判断矩阵,对生态-水网系统进行综合评价,故目标层为生态-水网系统A。通过结构模型利用重要性标度法构造出判断矩阵A:

1.2 熵值法
熵值法根据数据的无序程度确定权重。在信息论中,信息熵值越大,信息的无序度越高,其信息的效用值越小[3]。进行指标量化的计算步骤如下。
(1)构建数据矩阵。构造由研究年数(m)和指标(n)组合的原始数据矩阵C=[Cij](i=1,2,…,n;j=1,2,…,n),Cij为第i个样本,第j项指标值。
(2)对原始数据进行无量纲化处理,得到无量纲化数据矩阵Y=[Yij]。
(3)信息熵值ej和信息效用值dj。第j项指标信息熵ej的值:,式中的k与系统中的m有关,k=1/1n m,0≤e≤1。当一个信息系统是无序状态时,e=1,此时ei对总和评价的效用值为0。则某项指标的信息效用值dj取决于该指标的信息熵ej与1的差值,即:dj=1-ei。
(4)指标权重的确定。评价指标的价值系数越高,对评价的重要性越大,其对应的权重也越高。因此,第j项指标的权重为
1.3综合评价模型的建立
熵权是客观的权重,体现了在决策的客观信息中指标的评价作用大小。而层次分析法是决策过程中主观的权重,反映了决策者对决策指标的偏好。综合权重的计算步骤如下。
通过层次分析法得到m个指标的主观权重(θi)。通过熵值法计算熵权(ωi)。按照公式λi计算综合权重[4]。
2 案例应用
以河北省为例,分析2008-2012年生态-水网复合系统,具体步骤为以下4个主要方面:选择评价指标,进行原始数据整理,指标数据处理,权重求解。
2.1 评价指标选择
根据河北省的生态特征选择生态丰富指数、植被覆盖率,水网密度指数,土地退化指数,污染物负荷指数等五个指标对生态质量进行评价。根据水环境主要面临的问题:水资源严重缺乏、地表水明显减少、地下水严重超采,以及水污染严重,将水网系统的指标设定为人均水资源量,总体水质级别,地下水开采率,垃圾无害率,年平均降水量等五个指标。具体指标体系如表1。
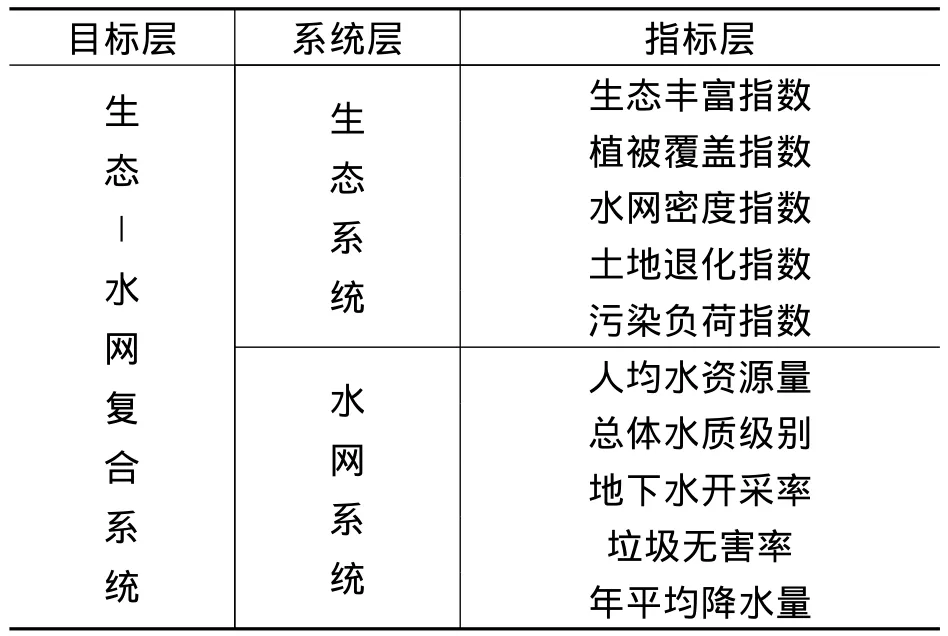
表1 河北省生态-水网复合系统指标体系Tab.1 Index system of ecological- water network complex system in Hebei province
2.2 指标数据处理
本案例的数据来源为《河北省环境状况公报》(2008-2012年)。
生态系统中的5个指标值依据《生态环境状况评价技术规范(试行 HJT192 -2006)》[5]进行计算。

表2 河北省生态—水网系统指标值Tab.2 parameter values of ecological - water network system in Hebei province
在水网系统中选取对数函数数学模型y=a+b×1g x对5个指标进行无量纲化处理[6]。
2.3 权重计算
层次分析法指标权重计算。根据河北省生态-水网质量综合评价层次结构模型,层次之间A-B、B1-C、B2-C 的判断矩阵分别见表 3,表 4,表5;各判断矩阵及计算结果见表6,C层对于A层的权重计算见表7。
熵值法计算指标权重。根据熵值法计算指标权重的步骤,分别求出信息熵值,信息效用值,最后确定指标权重。具体数值见表8。
综合权重计算。根据表7中层次分析法得到指标的主观权重(θi)以及表8中熵值法得到的熵权(ωi),按照公式计算综合权重。

表3 A-B比较判断矩阵Tab.3 A - B comparative judgment matrix

表4 B1-C比较判断矩阵Tab.4 B1 - C comparative judgment matrix

表5 B2-C比较判断矩阵Tab.5 B2 - C comparative judgment matrix

表6 层次单排序表Tab.6 Table of single sorting level
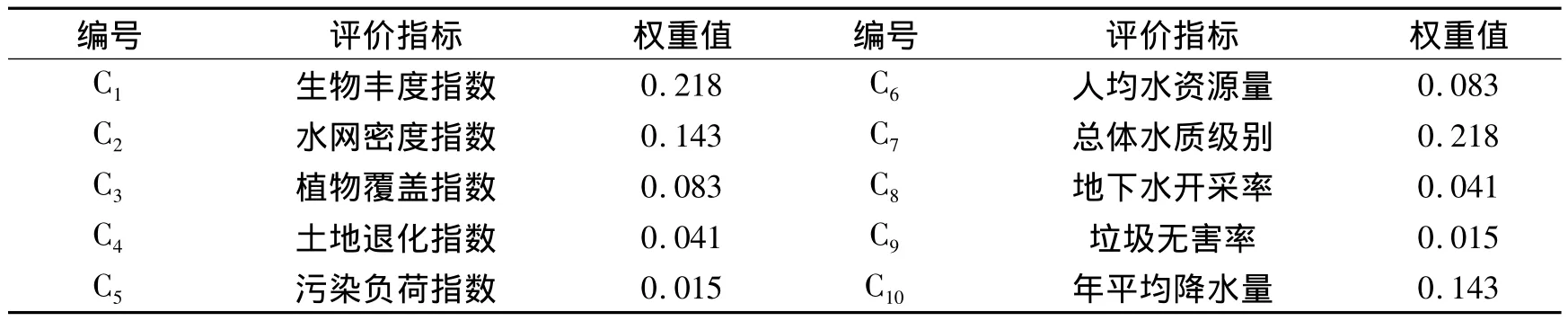
表7 基于AHP的指标权重值Tab.7 Table of index weight based on the AHP

表8 基于熵值法的指标权重计算表Tab.8 Table of index weight calculation based on the entropy value method
3 结论
1)生态丰富指数、植被覆盖率、总体水质级别等3个指标对复合系统的影响最大,这对河北省的生态—水网复合系统的评价和治理起到了一定的借鉴作用。
2)本文构建的指标量化流程以及AHP-熵值法模型可以保证在指标完备的基础上,优化指标数,减少指标干扰,量化指标,可为后续的复合系统的耦合模拟以及管理评价奠定良好基础。
[1]宋新山,邓 伟.环境数学模型[M].北京:科学出版社,2004.
[2]李 恺.层次分析法在生态环境综合评价中的应用[J].环境科学与技术,2009,32(2):183 -185.
[3]马建琴,郭晶晶,赵鹏.基于主成分分析和熵值法的景观水水质评价[J].人民黄河,2012,34(3):36 -38.
[4]韦新良,马俊,刘恩斌,等.生态景观林树种选择适宜性评价技术研究[J].西北林学院学报,2008,23(6):207- 212.
[5]HJ/T192-2006,生态环境状况评价技术规范(试行)[S].
[6]赵庆建.河北省水环境安全评价体系及水资源可持续利用技术研究[D].哈尔滨:哈尔滨工业大学,2007.
[7]王月,李东亮.基于层次分析法的采石场生态恢复植物选择[J].河北工程大学学报:自然科学版,2013,30(03):96-99.

