位移边界对2D-FGM板热应力影响研究
许杨健,刘文芝
(河北工程大学土木工程学院,河北邯郸056038)
功能梯度材料(Functionally Graded Materials,简称FGM)是一种新型的特殊复合材料[1-2],优于传统复合材料的特性,已成为材料领域研究的重点及多学科交叉领域的研究热点[3-7]。因 FGM在超高温工作环境中的应用日益广泛,故分析该材料组成物体的热应力场特别是瞬态问题更具实用价值。
国外Obata[8]等采用摄动法对加热、冷却过程中的常物性FGM板瞬态热应力进行了研究,但是这种方法过于繁复,不便于工程应用。在前面的研究工作基础上,本文采用有限元法,对处在不同的位移边界条件下的常物性2D-FGM板冷却瞬态热应力问题进行研究分析,其结果对FGM的生产和应用具有重要的指导意义。
1 研究模型
如图1所示,选定二维常物性Al1100/Ti-6Al-4V/ZrO2FGM板作为分析模型,其平面结构长度l=40 mm、厚度b=10 mm,且假设:(1)该FGM 平面区域具有长度x与厚度y方向任意分布及连续变化的材料物性性质;(2)FGM平面区域的温度初始条件和加热边界条件为:初始温度为常温T0,当时间t>0时,在区域的四周表面外侧分别施加第一类加热边界温度Ta、Tb、Tc及Td并保持不变;(3)分析模型前后表面绝热,内部无内热源,且不考虑热固耦合项作用影响。

图中,k,ρ,cρ,E,ν以及α分别是FGM 的热导率、密度、比热,弹性模量和线热膨胀系数。
1.1 位移边界条件
为研究外部约束对常物性2D-FGM板平面区域冷却瞬态热应力分布的影响,本文选取4种位移边界条件,即简支、一端固定、两端固定、四周固定,分别如图 2 中 a、b、c、d 所示。
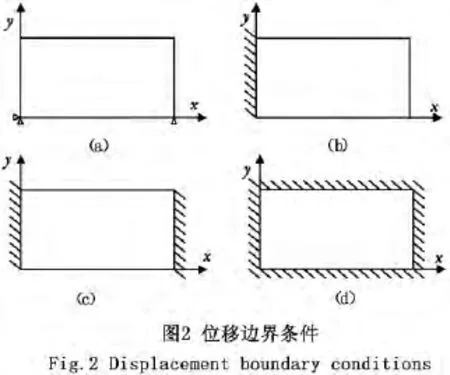
1.2 平面结构和加热、冷却边界条件
使用网格自动划分程序对上述研究模型平面区域进行网格剖分,在x方向上划分80层,即选定81条纵向线段,每一条线段上取21个节点,将该平面区域划分为3 200个单元,1 701个节点。瞬态时间步长Δt取0.1,并给出换热边界条件:
加热时,板的周边第一类换热边界条件为

冷却时,板的周边第一类换热边界条件为

式(1)、式(2)中的Ta,Tb,Tc和Td是平面矩形区域的四周边界温度,T0为初始温度。
2 热传导和热应力有限元基本方程
2.1 热传导有限元基本方程
首先将整个平面区域离散成M个简单的三角形单元,单元面积为Se使其3个节点编号i、j、m按逆时针旋转,其中对于边界单元而言,编号i表示内部节点,编号j和m表示边界节点。并且时间过程划分为n个间隔Δtn,n=2,3,…,N。全部节点在瞬时tn-1的温度值为列矩阵。在Δtn内,常物性 FGM板瞬态热传导有限元基本方程为[9]

式中H、Q—温度刚度矩阵和变温系数矩阵;T—未知温度值的列向量。
2.2 热应力有限元基本方程
设图1所示常物性2D-FGM板的热学性质为位置坐标x、y的函数,且在每一坐标平面内材料具有各向同性的性质,则该板的应变分量和应力分量分别为[10]

式中E(x,y)、a(x,y)、v(x,y)、θ(x,y,t)—弹性模量、线性热膨胀系数、泊松比、温变函数;u和v—单元e内任一点(x,y)的横向位移和纵向位移。
对于热弹性问题而言,计算应力场得先计算温度场,故此处的网格划分与热传导网格划分完全相同。则常物性FGM板瞬态热应力有限元基本方程为[9]

此线性代数方程的解就是整个求解区域在tn时刻,所有节点位移u1,u2,…,uL及v1,v2,…,vL。
3 本研究方法正确性检验
3.1 热传导正确性检验
为了验证本文有限元程序的正确性,我们应用有限元法与分离变量法求解上述特殊非均匀材料平面热传导问题的同一算例。设平面矩形区域宽为l=10 mm,厚为b=10 mm,参数D=E=1,c=d=0.1。并将该区域划分为441个节点,800个单元,整个区域初始温度300 K,且区域四周均作用第一类边界条件。利用有限元程序计算该材料平面温度场,并从中取得t=1.0 s,3.0 s,5.0 s 时的温度场值,并将其同利用分离变量法计算所得的结果形成对比,如表1所示。
观察表 1 可知:t=1.0 s、t=3.0 s、t=5.0 s时平面区域水平中线上11个点的温度值的分离变量解和有限元解最大误差分别为 0.44%、0.36%、0.25%,并分别为(7,5)、(5,5)、(9,5)的点。由上述分析可知,利用分离变量法和有限元法求得的两种温度解存在的最大误差都远小于5%,是能满足实际工程需求的。
3.2 热应力正确性检验
为检验热应力计算部分有限元程序的正确性,我们取一简支梁作为算例,设其模型为2l=100 mm,h/2=5 mm,上边界作用均布荷载q,两端作用反力ql保持平衡,且不计体力,温变函数θ=θ0(1-4y2/h2)为已知(θ0为常数),线热膨胀系数α=0.000 001/K,泊松比ν=0.3,弹性模量E=200 GPa。利用网格自动划分程序将模型划分为101条纵向线段,21条横向线段,每条纵向线段间隔为1.0 mm,每条横向线段间隔为0.5 mm,即网格划分为2 121个节点,同时获得解析解所需要的区域节点坐标。如图3所示。

首先给出简支梁应力分量计算表达式:


表1 温度场正确性检验Tab.1 Testifying temperature distribution accuracy

我们只求解简支梁仅在温度荷载作用下的热应力,令q=0,θ0=300。通过式(7)、式(8)、式(9)计算该问题热应力σx的解析解,通过有限元法计算得到其数值解。给出简支梁x坐标为0.0的纵向线(y轴)上热应力的解析解和有限元解,并将两者的计算结果进行对比。如表2所示。
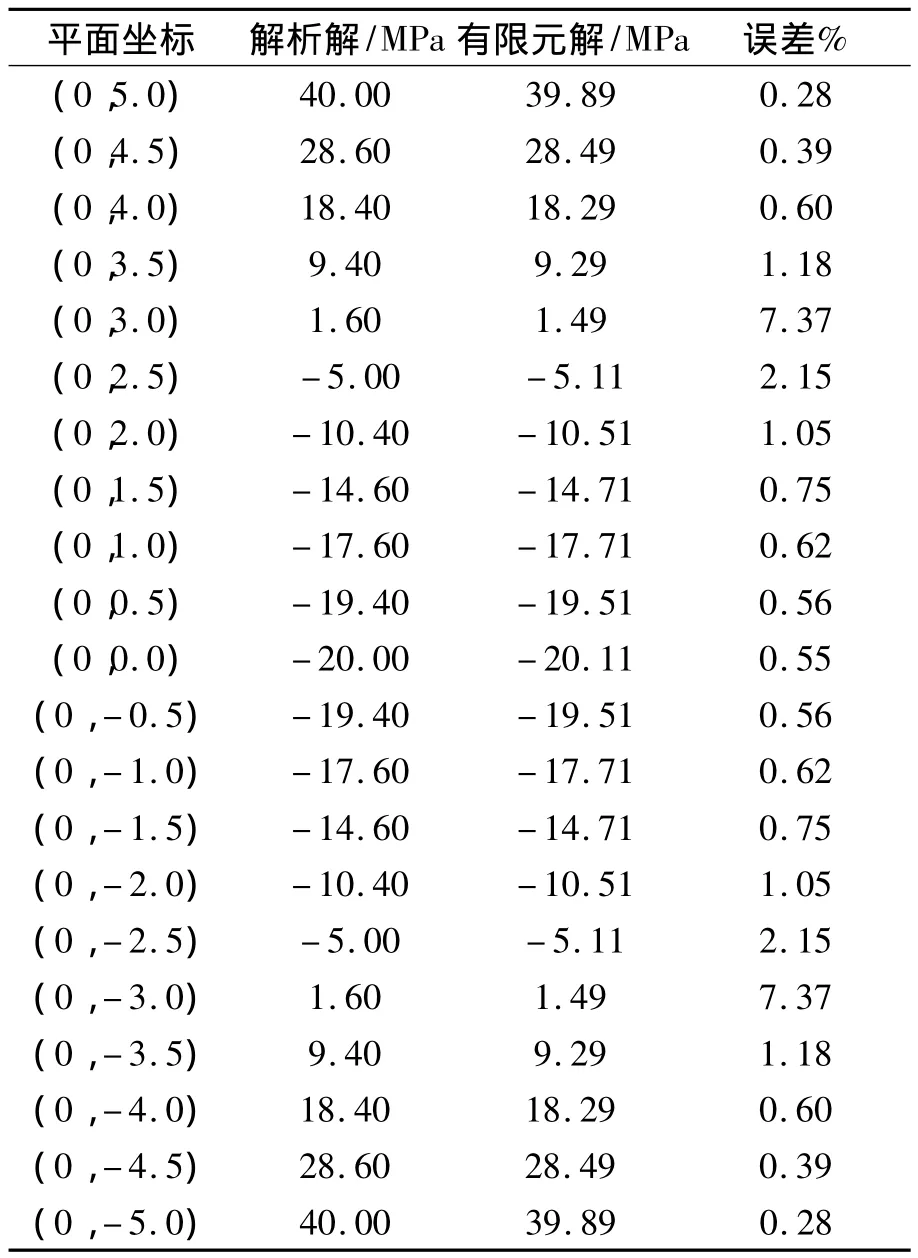
表2 温变下的简支梁平面热应力Tab.2 Plane thermal stress of simple supported beam under temperature variation
从表2可以发现:两者解法的最大误差为7.37%,显然误差较大,但如果在应力值都只保留1位有效数字的情况下,误差将均为0%,加之应力值本身也很小,故仍可认为有限元计算结果是有效的。
4 热应力场分布和分析
如图1所示模型,取组分形状分布系数mx和my为1.0,孔隙率控制参数Ax和Ay取0.0,nx、ny、zx和zy均取为1.0,其换热边界条件为前面所述式(1)和式(2),按图2所示的外部约束,即简支、一端固定、两端固定和四端固定4种位移边界条件,得到t=1.0 s时的冷却瞬态热应力场分布图形,如图4所示。

我们知道,位移边界的不同是不会引起温度场变化的,那么在各种计算相同,换热边界条件相同的情况下,常物性2D-FGM平面区域的温度场分布在不同位移约束条件下应当是保持一致的。并且根据热弹性力学理论,若FGM平面区域的左右两个边界是自由边界,那么边界上的热应力σx=0。
分析图4可知:冷却情况下,位移边界条件对常物性2D-FGM平面区域冷却瞬态热应力分布影响颇大。
观察图4(a)和4(b)可知,在简支情况下,平面区域的左右两个边界都是自由边界,在一端固定情况下,平面区域的右边界是自由边界,因此,这些边界上的热应力σx=0;从图4(a)变化到图4(b),即将左边界设置为固定约束后,在平面的左边界上形成了上中下三个应力聚集,但应力值几乎没有发生变化,整个区域既存在压应力又存在拉应力。
图4(c)中,将左右边界均设置为固定约束后,其右边界不仅也产生了相同现象,而且区域内部应力分布形状与数值都发生了巨大变化:平面中部应力分布曲线更加不平行于x坐标方向,区域内部应力值全部成为拉应力,且数值增长幅度颇为显著;将四周均设置呈固定约束后,如图4(d)所示,平面四角上的应力聚集消失,热应力数值增长幅度较两端固定情况时更为明显。
5 结论
冷却过程中,位移边界条件对常物性2DFGM平面区域冷却瞬态热应力分布影响颇大,将四周均设置呈固定约束后,平面四角上的应力聚集消失,应力凸起位置移动到平面右上部位,热应力数值增长幅度较两端固定情况时更为明显。
[1]李信,刘海昌.功能梯度材料的研究现状及展望[J].材料导报,2012,26(19):370 -372.
[2]马涛,赵忠民,刘良祥,等.功能梯度材料的研究进展及应用前景[J].化工科技,2012,20(1):71-75.
[3]WUXIANG LIU,ZHENG ZHONG.Three-dimensional thermoelastic analysis of functionally graded plate[J].Acta Mechanica Solida Sinica,2011,24(3):241 -249.
[4]许杨健,涂代惠,马士进.加热、冷却下变物性梯度功能材料板瞬态热应力[J].机械强度,2005,27(4):510-517.
[5]M R GOLBAHAR HAGHIGHI,P MALEKZADEH,H RAHIDEH,et al.Inverse Transient heat conduction problems of a multilayered functionally graded cylinder[J].Numerical Heat Transfer,Part A:Applications.2012(9):717-733.
[6]许杨健,王飞,杜海洋.初始和边界恒温时二维梯度板瞬态温度场[J].固体力学学报,2014(2):3-6.
[7]许杨健,王飞,杜海洋,等.边界不同恒温时功能梯度板平面稳态温度场[J].河北工程大学学报:自然科学版,2013,30(2):4 -8.
[8]OBATA Y,NODA N.Unsteady thermal stresses in a functionally gradient material plate(Analysis of one-dimensional unsteady heat transfer problem)[J].Trans.JSME,1993,59(560):1090 -1096.
[9]王洪纲.热弹性力学概论[M].北京:清华大学出版社,1989.
[10]严宗达,王洪礼.热应力[M].北京:高等教育出版社,1993.

