基于梯度和贝叶斯判别的夹层自动识别方法
张庆国,葛云龙,李一赫
(东北石油大学地球科学学院,黑龙江大庆163318)
夹层是指位于单砂层内部的相对低渗透层或非渗透性岩层,是陆相储集层中流体非均质流动形成的主要原因之一。当油田进入高含水期采油阶段,隔夹层会产生渗流屏障和渗流差异的现象,对水驱油的过程会产生很大影响[1-3]。然而人为识别夹层工作量大,现存的定量区分的方法应用效果不理想[4-8]。为此,笔者分析扶余油田夹层测井相应特征,建立基于梯度和贝叶斯判别的夹层自动识别方法,以期实现夹层的自动化划分。
1 夹层自动划分方法
1.1 测井曲线主成分分析
各个井的测井系类不一,为了统一处理,需要对所有测井系类进行主成分分析,从而选取可以代表所有测井系类的曲线。由于测井曲线单位不一,数值大小范围相差甚远,故在进行主成分分析之前,首先对测井曲线进行标准化处理。选取各类夹层的测井曲线,根据式(1)进行标准化处理[9]。
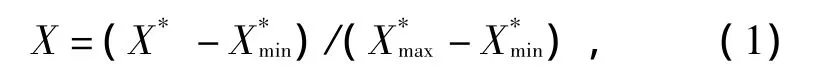
式中:X——归一化后的数据,X∈[0,1];
X*——原始数据;
对标准化处理后的测井曲线进行相关系数计算,得到相关系数矩阵,根据相关系数矩阵计算特征值λ,从而计算主成分贡献率和累计贡献率,最终得到可以代表所有测井系类的曲线。构成第一主成分和第二主成分的各测井曲线系数如表1所示。由式(2)、(3)计算得第一主成分和第二主成分累计贡献率为87.751%。
主成分贡献率

累计贡献率
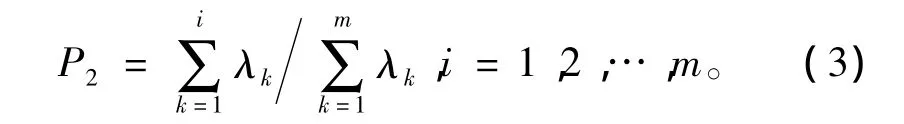
由于存在多种测井曲线反映同一种特征现象,为了简化,故从表1中选择ρRLLS、GR、ρRLLD、CAL、AC为判别夹层的测井曲线。
1.2 新测井曲线的构造
当地层无夹层发育且仅仅是储集层内细微的粒度以及物性变化时,测井曲线相对平滑[10]。对各类反映夹层的测井曲线进行滤波后,原始值与新构建的曲线在夹层出现时会出现明显的差值,所以利用算术平均滤波法对测井曲线进行平滑处理。研究发现,滤波窗口大小会影响识别夹层的准确性。经过多次实验后,采用11点滤波,并在窗口内去除最大值和最小值,使得到的曲线尽量不受夹层等因素影响。X井滤波前后测井曲线对比结果如图1所示。

表1 各曲线主成分系数Table 1 Each curve principal component factor
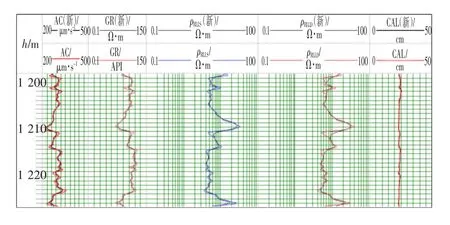
图1 X井滤波前后测井曲线对比Fig.1 X well filtering and original curves comparison chart
1.3 测井曲线尖峰和低谷的确定
由于泥质夹层和物性夹层在测井曲线上表现为低凹的电阻率曲线,自然伽马曲线(GR)、有异常幅度回返,钙质夹层在测井曲线上,电阻率为高值,声波时差(AC)相对降低,故针对该地区地质条件,设定测井曲线的回返程度(图2)和各类夹层原有曲线、新曲线的差值门槛。对于钙质夹层,设定电阻率增大量大于原来的15%,声波时差差值小于0;对于泥质夹层和物性夹层,设定电阻率差值小于0,自然伽马差值大于0,得到符合条件的“尖峰”和“低谷”。

图2 深侧向电阻率回返程度Fig.2 Deep lateral resistivity returning extent
1.4 夹层类型的确定
根据该地区夹层的测井曲线特征,选取泥质夹层、物性夹层、钙质夹层各三个,共读取36个数据点,将数据以每个砂体为单元进行标准化后带入式(4),建立各类夹层的Bayes判别模型[9]。
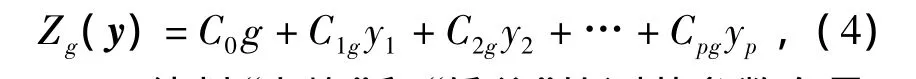
式中:y——待判“尖峰”和“低谷”的测井参数向量,y=(y1,y2,…,yp)T;
C——判别系数。
根据各类样本的测井参数计算求得各类夹层判别公式:
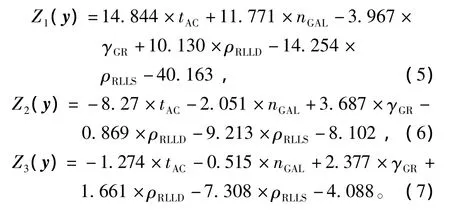
式中:tAC——声波时差;
γGR——自然伽马曲线;
nGAL——GAL值。
将各测井曲线值分别代入式(5)~(7),如果Z1(y)为正数,Z2(y)、Z3(y)为负数,则为钙质夹层;如果Z2(y)为正数,Z1(y)、Z3(y)为负数,则为泥质夹层;如果Z3(y)为正数,Z1(y)、Z2(y)为负数,则为物性夹层。
对36个数据点样本进行回归检验,正确率为100%。应用判别公式时,首先对每个“尖峰”和“低谷”进行以砂体为单元的标准化处理,之后将数据点带入判别公式进行夹层类型判别。
1.5 梯度判别
由于自然伽马变化梯度(GR)、深侧向变化梯度(RLLD)、声波时差变化梯度(AC)三个参数在该地区反应夹层的性质方面更加灵敏,故利用这三个参数识别夹层的性质[10]。
梯度是指单位距离内原始测井曲线偏离滤波后的测井曲线差值多少,对每个“尖峰”和“低谷”进行梯度判别。以深侧向电阻率变化梯度为例,计算式如下:

式中:dRLLD——梯度,Ω;
ΔρRLLD——深侧向电阻率变化量,Ω·m;
ρRLLDY——原始深侧向电阻率值,Ω·m;
ρRLLDX——新深侧向电阻率值,Ω·m;
Δh——该“尖峰”和“低谷”的厚度,由半幅点确定,m。
钙质夹层、泥质夹层、物性夹层测井曲线梯度特征如图3所示。
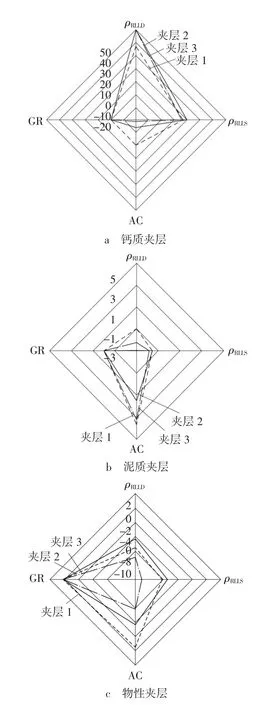
图3 不同夹层测井曲线梯度特征Fig.3 Different interlayer log gradient feature
从图3可以看出,钙质夹层深侧向电阻率梯度大于30 Ω;泥质夹层深、浅测向电阻率梯度大于-3 Ω小于0 Ω;而物性夹层深、浅测向电阻率梯度小于-4 Ω。
2 应用效果
2.1 计算结果与取心结果对比
综合利用BAYES判别模型和梯度判别的方法,对扶余油田VI区块进行划分。以其中一口井为例,与取心井进行对比,结果如表2所示。对于取心井共识别出10个夹层,其中八个符合,通过对岩心识别发现,当小层较薄且周围岩性有一定变化时,很有可能误认为夹层,如图4所示。
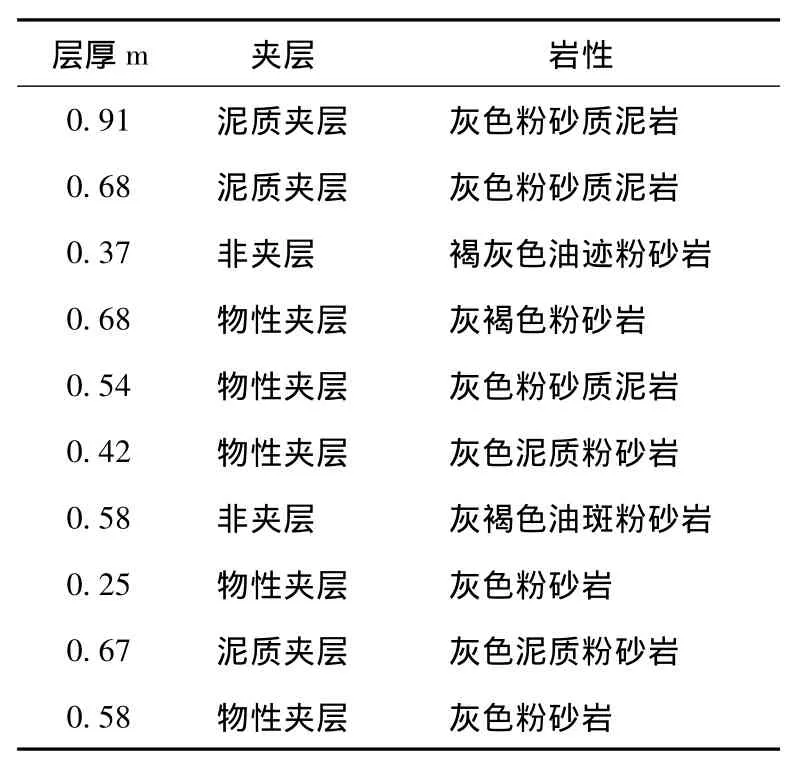
表2 岩心识别校对夹层Table 2 Core identification proof sandwich
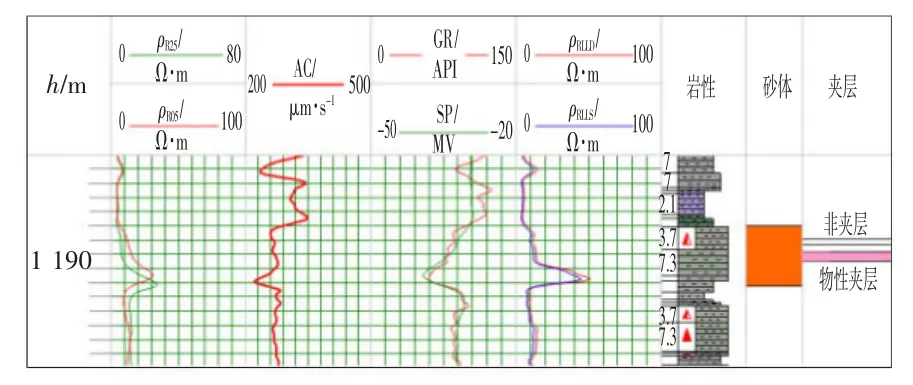
图4 非夹层的综合解释Fig.4 Non interlayer comprehensive interpretation picture
图5为取心井XX的夹层自动识别结果。从图5中可以看出,深侧向电阻率梯度、浅测向电阻率梯度、声波梯度为负数时,一般为物性夹层;深侧向电阻率梯度、浅测向电阻率梯度为负数,声波梯度为正数时,一般为泥质夹层;深侧向电阻率梯度、浅测向电阻率梯度为正且声波梯度很大正时,一般为钙质夹层。上述结果表明,该方法提高了对夹层的判别精度。

图5 XX井夹层判别结果Fig.5 XX well discriminating result
2.2 计算结果与沉积环境对比
应用分类得到的夹层,绘制整个工区夹层的平面分布图,如图6所示。

图6 X层夹层平面Fig.6 X layer inter layer plan
由于工区断层较少,且成中部高、南北低的地势,不发育,所以,其夹层的分布受构造影响较小,但夹层的分布受沉积相影响较大,而识别出的夹层与沉积中的河道(图7)分布比较吻合。
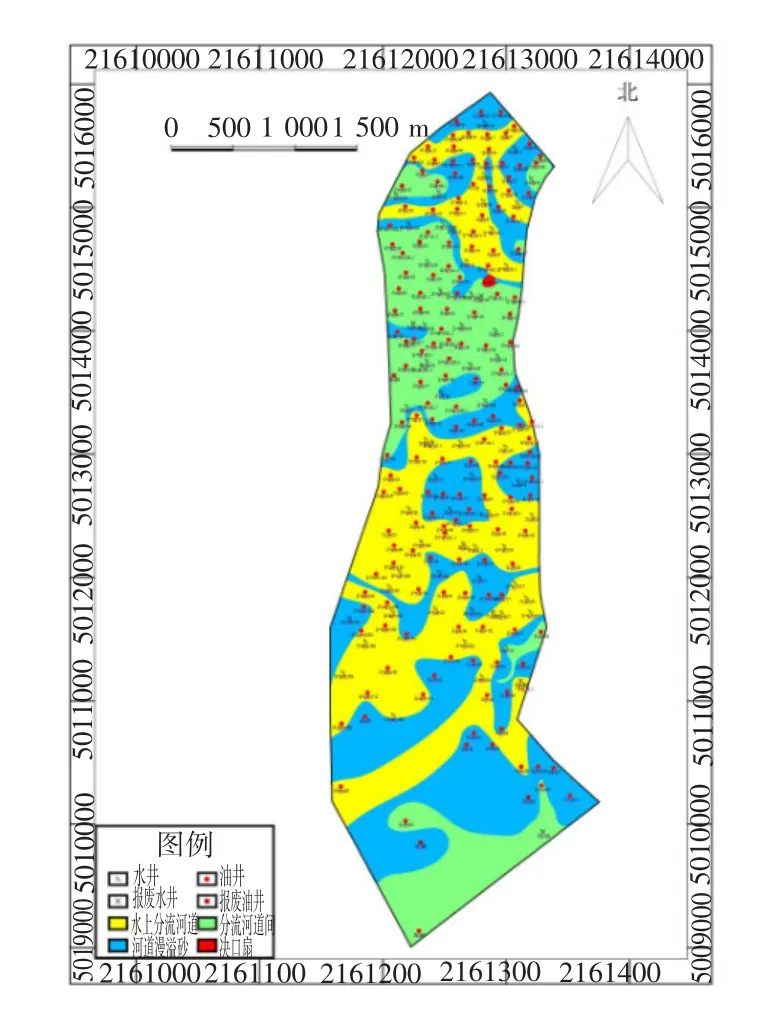
图7 X层沉积微相平面Fig.7 X layer deposition microfacies plan
3 结束语
文中所提出的夹层自动划分方法,首先分析测井曲线主成分,得到适合判别夹层的曲线。之后,对曲线进行滤波,使之尽量不受夹层等因素干扰。再以回返程度和各类夹层原有曲线和新曲线的差值门槛为条件,得到“尖峰”和“低谷”。通过建立的夹层类型判别模型,结合梯度判别,最终实现夹层的自动划分。对比分析结果验证了该方法的准确性。
[1] 陈程,孙义梅.厚油层内部夹层分布模式及对开发效果的影响[J].大庆石油地质与开发,2003,22(2):24-28.
[2] 李阳.储集层流动单元模式及剩余油分布规律研究[J].石油学报,2003,24(3):52-55.
[3] 王延章,林承焰,温长云,等.夹层分布模式及其对剩余油的控制作用[J].西南石油学院学报,2006,28(5):6-10.
[4] 李阳,王端平,刘建民.陆相水驱油藏剩余油富集区研究[J].石油勘探与开发,2005,32(3):91-96.
[5] 阎海龙,孙卫.水下分流河道砂体中夹层的识别及定量分析——以靖安油田盘古梁长6油层为例[J].西北大学学报:自然科学版,2006,36(1):133-136.
[6] 张吉,张烈辉,胡书勇.陆相碎屑岩储集层隔夹层成因、特征及其识别[J].大庆石油地质与开发,2003,22(4):1-3.
[7] 郭长春,李阳.河流相储集层中夹层的发育规律及预测[J].石油天然气学报(江汉石油学院学报),2006,28(4):200-203.
[8] 林博,戴俊生,陆先亮,等.孤岛油田中一区馆5段隔夹层划分与展布[J].西安石油大学学报:自然科学版,2006,21(4):11-14.
[9] 曹翠.胜坨油田一区沙二段储层夹层定量表征[D].北京:中国石油大学,2010.
[10] 辛治国,冯伟光,郭士博,等.夹层自动识别方法[J].新疆石油地质,2010,31(3):307-310.
——以加拿大麦凯河油砂储集层为例
- 黑龙江科技大学学报的其它文章
- 镁合金表面氩弧熔覆Al-Si基SiC复合涂层组织及耐磨性
- 采煤机液压调姿牵引机构的仿真研究

