基于AHP-ACO模型的区域水资源承载力评价

李晓花

(巴州新宇水利水电工程咨询有限责任公司，新疆库尔勒市 841000)

文章编号：1006—2610(2015)05—0016—05

基于AHP-ACO模型的区域水资源承载力评价

李晓花

(巴州新宇水利水电工程咨询有限责任公司，新疆库尔勒市 841000)

正确评价区域水资源承载力，对合理开发利用水资源以及促进区域社会经济的可持续发展具有重要意义。以新疆和田地区为例，利用层次分析法的层次框架思维模式与蚁群算法的自适应性及人为干扰少等特点，构建了层次分析-蚁群算法。采用层次分析法获得评价指标权重值，再利用蚁群算法确定研究区不同年份的优属度。结果表明：研究区历年水资源承载力等级均为Ⅱ级；其中，2012年的水资源承载力值最高，2011年的水资源承载力值最低，评价结果符合研究区实际情况。

水资源承载力；层次分析法；蚁群算法；和田地区

0 前 言

水资源承载力是衡量区域可持续发展的一项重要指标。客观、正确地评价区域水资源承载力，对合理开发利用水资源以及促进区域社会经济的可持续发展具有重要的现实意义。

目前针对水资源承载力的评价方法主要有主成分分析法、可拓评价法、人工神经网络法、层次分析法、模糊数学理论法、灰色关联法、基于熵权的TOPSIS法等[1-5]。上述方法虽然对水资源承载力评价具有一定指导意义，但模糊综合评价模型不能很好地将承载力评价体系中需要突出的指标体现出来，因而降低了评价结果的精度；灰色关联法和人工神经网络模型在计算中需要水资源承载力等级标准，而这种标准目前中国还没有形成，计算结果在现实中难以应用；层次分析法计算较为简单，但评价指标的主观性较大，评价结果存有偏向性[6]。

蚁群算法是将自然界中的蚂蚁觅食规律及在觅食行动中的相互协作规律进行优化的模拟算法[7]。它是一种在没有外界作用下使得系统墒增加的自组织算法。人工蚂蚁间通过信息激素的作用，自发地趋向于寻找接近最优解的一些解，是一个无序到有序的过程。蚁群算法具有较强的全局搜索能力与鲁棒性。但其信息素庞大，搜索时间较长，会导致部分信息缺失，降低了评价结果的可信度。层次分析法为层次思维框架，通过对比进行标度，增强了科学性和实用性，但当评价因素过多时，标度工作量大，易引起判断混乱；而且其对标度出现负值的情况考虑不足，矩阵判断讨论较多时对其合理性考虑不够[8-9]。本文将层次分析(analytic hierarchy process,AHP)与蚁群算法(ant colony optimization,ACO)结合(AHP-ACO)，取长补短，用于水资源承载力评价中指标权重的确定，可使权重的确定更客观。

鉴于此，本文以新疆和田地区为例，建立了由16项评价指标构成的水资源承载力评价体系，对其2005—2012年水资源承载力变化情况进行评价。采用AHP确定水资源承载力评价指标权重，然后利用ACO确立评价指标体系及其参数，旨在建立更加适合于区域水资源承载力评价的简易模式，为水资源开发利用综合评价提供一条新思路。

1 水资源承载力评价体系构建

遵循科学性、实用性、便捷性和针对性的原则，结合新疆和田地区水资源开发利用现状，建立研究区水资源承载力综合评价指标体系。该体系包括4个方面、16项指标[10]。4个方面包括水资源系统、社会系统、经济系统和生态环境系统。其中水资源系统包括人均水资源量(C1，m3)、水资源开发利用率(C2，%)、单位面积水资源量(C3，万m3/km2)与供水模数(C4，万m3/km2)这4项指标；社会系统包括人口密度(C5，人/km2)、人口自然增长率(C6，‰)、城镇化率(C7，%)、农村饮用水不安全率(C8，%)4项指标；经济系统包括人均GDP产值(C9，元)、GDP年增长率(C10，%)、耕地灌溉率(C11，%)与第一产业占GDP比例(C12，%)这4项指标；生态环境系统包括林草地覆盖率(C13，%)、生态环境用水率(C14，%)、地下水开采率(C15，%)与工业废水处理率(C16，%)这4项指标。和田地区水资源承载力评价指标体系详见表1。

根据水资源承载力和社会经济发展对水资源的压力程度，将水资源承载力划分为5个等级，其中：I级表示水资源承载力为极强等级，此时水资源开发利用处于起步阶段，开发潜力巨大；Ⅲ级表示水资源承载力为中等级别，此时水资源开发利用已有一定规模，但仍有较大的开发潜力；V级为水资源承载力极弱等级，此时水资源承载力已接近饱和，开发潜力极小。Ⅱ级和Ⅳ级属于过渡等级，水资源承载力等级的量化标准见表2。

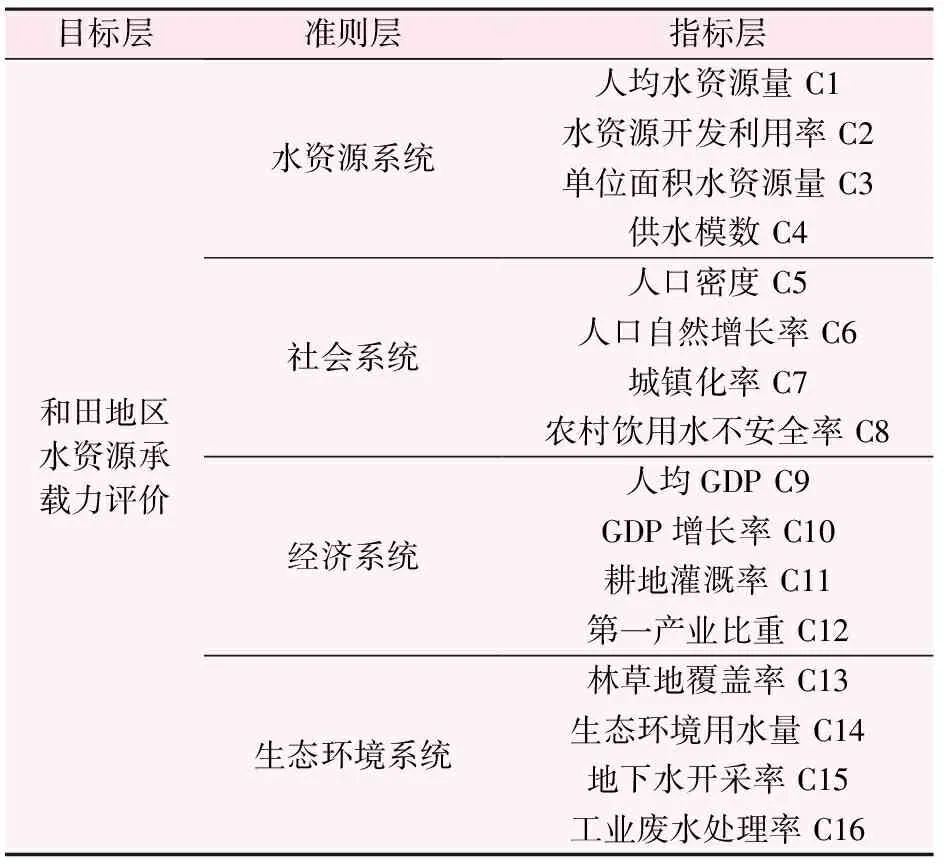
表1 和田地区水资源承载力评价指标体系表

表2 和田地区水资源承载力评价指标分级标准表

2 AHP-ACO综合评价方法

2.1 评价指标标准化

为了消除评价指标的量纲和数量级别对模型的影响，建模前先采用式(1)和式(2)分别对正向指标与负向指标进行归一化处理：

；j=1,2,…,m)

(1)

；j=1,2,…,m)

(2)

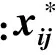
2.2 权重分配及检验

评价指标分为2个层次(见表1)，根据式(3)和式(4)，确定各层内不同指标的初始权重值：

(3)

(4)

式中：bi为构建的判断矩阵；wi为权重系数。通过计算一致性比率(CR)，对构建的判断矩阵bi进行随机一致性检验，判断各指标权重系数是否合理。当CR>0.1时，层次单排序结果一致性不合理，即各指标的权重系数不合理，需重新调整初始权重值，进行权重计算；当CR<0.1时，层次单排序结果具有比较满意的一致性，即各指标的权重系数比较合理。由此，可以获得指标的最终权重。

2.3 最佳投影方向的优化及最优方案的确定

据式(5)构建标准化加权值Xij：

(5)

依据式(6)得到投影到方向向量a=(a1，a2，a3，…，an)为m维单位向量，样本j在一维线性空间的投影特征值Zi在投影到方向向量ai=(a1，a2，a3，…，an)上的线性投影指标Zj：

(6)

据式(7)～式(10)确定目标函数Q(z)(即优属度)。当各指标值给定时，投影目标函数Q(z)只随着投影方向ai的变化而变化。不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向。

Q(z)=S(z)D(z)

(7)

(8)

(9)

(10)

最后，通过优属度进行各年份水资源承载力的综合评价，通过对各年份评价指标值的求取，选取每项指标的最大值作为最优值，把最优值作为最佳投影方向代入式(6)，得各年份的投影值Zi。将Zi与Zj进行比较，二者越接近，得到的优属度越小，表示越接近最优值。

3 模型应用

根据文献[10]数据资料，对新疆和田地区2005—2012年水资源承载力进行评价，研究区2005—2012年水资源承载力指标值见表3。

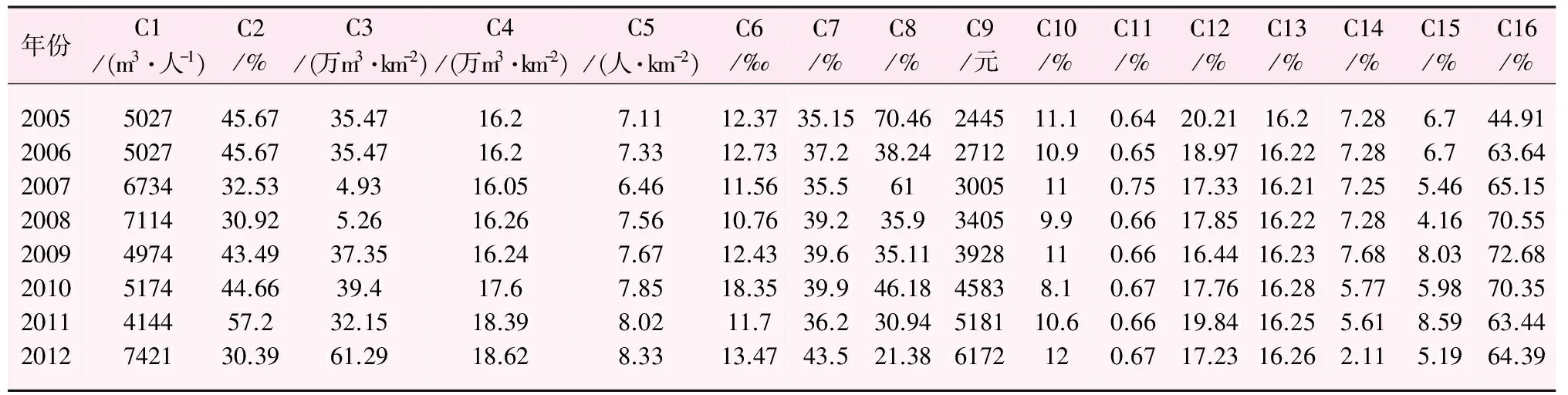
表3 和田地区水资源承载力评价指标统计值表

3.1 评价指标标准化加权值及其权重

权重反映了指标在评价过程中的重要程度，权重越大，说明该指标在评价中所起到的作用越大。由式(4)与式(5)计算求得的标准化加权指标可以反映出各指标在水资源承载力评价中的重要性，其结果见表4所示。标准化加权值Xij越大，说明第i年中第j项指标越好。

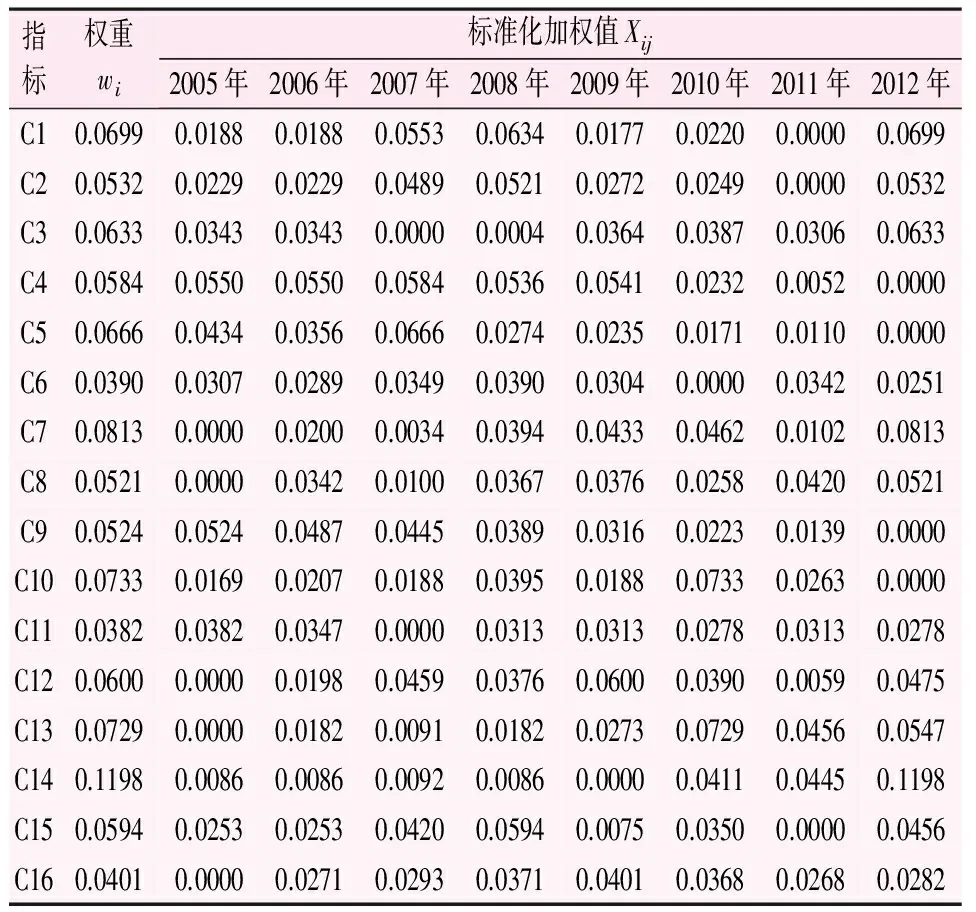
表4 2005—2012年和田地区水资源承载力评价指标标准化加权值与权重表

从表4可看出：16项评价指标的权重wi范围在0.03～0.12之间，差异较为明显。其中C14(生态环境用水量)权重最大，为0.1198；C11(耕地灌溉率)权重最小，为0.0382。

3.2 AHP-ACO模型评价

采用Matlab建立AHP-ACO模型，从各指标中选取最大值(最优值)见表5。利用最优值建立最佳投影方向向量，根据式(6)～式(10)求得不同年份的指标优属度Qz，结果见表6。优属度表征各指标标准化加权值与最优值的综合差距，差距越小，则该年份的水资源承载力综合评价越好。

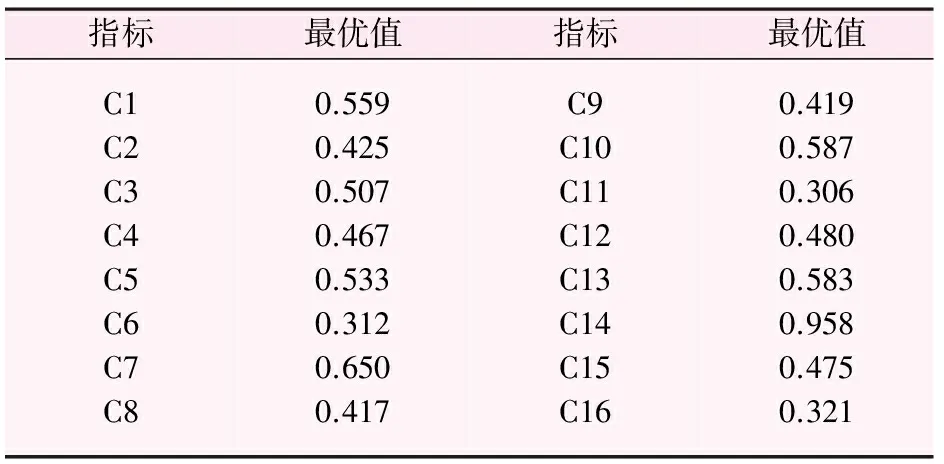
表5 各评价指标最优值表

从表6可以看出，和田地区2005—2012年的水资源承载力优属度分别为：2005年0.733 6、2006年0.654 8、2007年0.622 3、2008年0.610 2、2009年0.699 5、2010年0.721 7、2011年0.775 4、2012年0.558 7，其中2012年的优属度最小(最优)，为0.558 7。研究区历年水资源承载力状况均较好(水资源承载力等级均为Ⅱ级)。

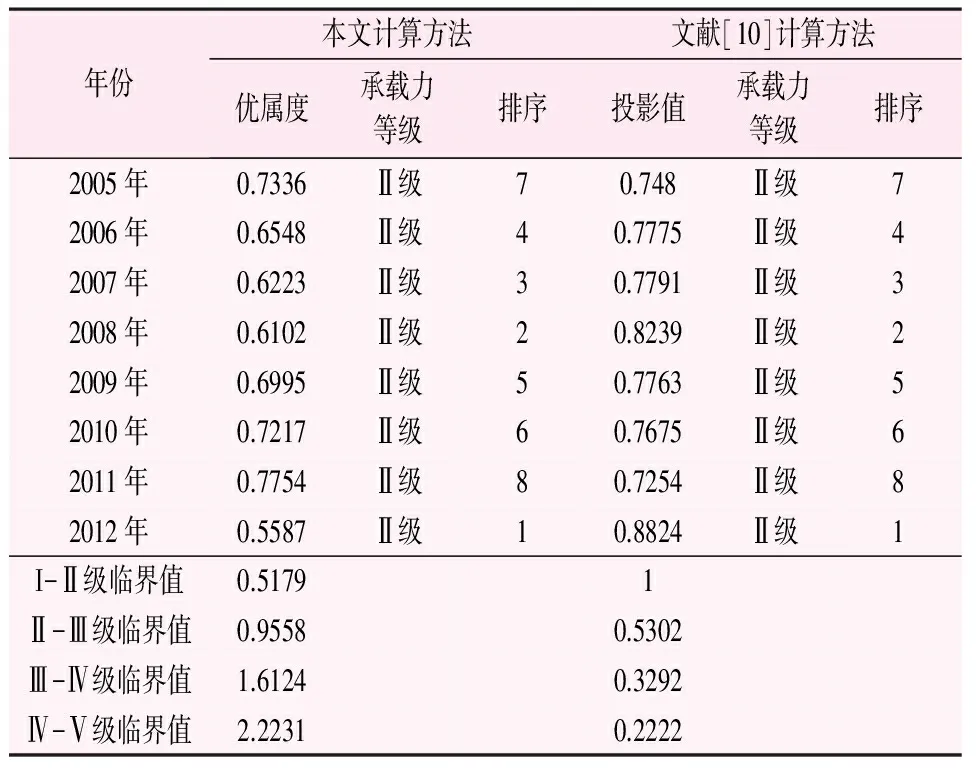
表6 2种模型评价结果对比表

3.3 评价结果验证

为了检验本文所建模型的准确性，利用文献[10]研究结果进行水资源承载力评价复核(结果见表6)。由表6可知，2种方法计算结果完全一致，这不仅验证了本模型的准确性，也实现了方法对方法的检验。

4 讨 论

本文采用AHP-ACO法评价区域水资源承载力，尽管效果良好，但也存在不足之处。如：运用AHP法难以避免专家判断水平及个人偏好等主观因素的影响；ACO法存在信息素积累过快、容易陷入局部过早收敛的缺陷，是制约ACO法搜索效率的主要原因。以后的研究可以尝试调整信息素更新机制、设计新的全局优化方法等方式克服这一缺陷。除此之外，由于水资源承载力评价指标的选取受自然、经济社会条件的制约与影响，本文所构建的水资源承载力指标体系还有一定的区域局限性，其在普适性方面还存在探讨。

5 结 论

本文以新疆和田地区2005—2012年水资源开发利用数据为基础，从水资源系统、社会系统、经济系统和生态环境系统4个方面建立了基于层次分析-蚁群算法(analytic hierarchy process-ant colony optimization)的水资源承载力评价模型，结果表明：研究区历年水资源承载力等级均为Ⅱ级，变化不大；水资源承载力优属度以2012年为最低、2011年为最高，表明研究区2012年的水资源承载力最好、2011年的水资源承载力最低。评价结果与实际情况较一致，说明AHP-ACO模型可用于区域水资源承载力综合评价，研究结果为区域水资源配置评价提供了一种新方法。

[1] 杨广,何新林,李俊峰.投影寻踪技术在水资源可持续利用评价中的应用研究[J].中国农村水利水电,2010,(11)：1-3,7.

[2] Chen H W, Chang N B. Using fuzzy operators to address the complexity in decision making of water resources redistribution in two neighboring river basins[J].Advances in Water Resources, 2010,33: 652-666.

[3] 许朗,黄莺.基于主成分分析的江苏省水资源承载力研究[J].长江流域资源与环境,2011,20(12)：1468-1474.

[4] 南彩艳,粟晓玲.基于改进SPA的关中地区水土资源承载力综合评价[J].自然资源学报,2012,27(12)： 104-114.

[5] 吕萍,刘东,赵菲菲.基于熵权的建三江分局水资源承载力模糊物元评价模型[J].水土保持研究,2011,18(2)：238-242.

[6] 雷雁斌,齐青青,费良军.大型灌区节水改造项目评价方法研究[J]. 沈阳农业大学学报,2008,39(2)：223-227.

[7] 封志明,郑海霞,刘宝勤. 基于遗传投影寻踪模型的农业水资源利用效率综合评价[J].农业工程学报,2005,21(3)：66-70.

[8] 寿涌毅,傅奥.多目标资源受限项目调度的多种群蚁群算法[J].浙江大学学报：工学版,2010,44(1)：51-55.

[9] 袁尧,刘超.基于蚁群算法的泵站运行优化及投影寻踪选优策略[J].农业机械学报,2013,44(3)：38-44.

[10] 吴雪梅,塔西甫拉提·特依拜.基于PSO-PPE模型的和田水资源承载力评价研究[J].干旱地区农业研究,2014,32(2)：28-233.

AHP-ACO Model Based Assessment on Bearing Capacity of Regional Water Resources

LI Xiao-hua

(Xinyu Water Resources and Hydropower Consulting Co., Ltd., Bayinguole Mongolian Prefecture,Kurle, Xinjiang 841000, China)

It is significant to correctly assess the bearing capacity of the regional water resources for the rational development and utilization of water resources as well as for the promotion of the sustainable development of the regional social economy. With the case of Hetian Prefecture, for example, the analytic hierarchy-ant colony algorithm is built by application of the thinking mode of the hierarchy frame of the analytic hierarchy process, self adaptability and few interference of the ant colony algorithm. By application of the analytic hierarchy process, the weight value of the index to be assessed is derived. Then, the ant colony algorithm is utilized to study the optimal subordinate degree in different years. The study shows that the carryover bearing capacity of water resources in the study region all are Class II. Among them, the bearing capacity of water resources in 2012 was at maximum and that in 2011 at minimum. Those are in compliance with the actual situation. Key words:bearing capacity of water resources; analytic hierarchy process; ant colony algorithm; Hetian Region

2014-12-29

李晓花(1980- )，女，新疆玛纳斯县人，工程师，主要从事水利工程规划设计工作.

TV213.9

A

10.3969/j.issn.1006-2610.2015.05.005