基于多维定标算法的WSN安全节点定位研究
郑学伟
(1.辽宁广播电视大学 辽宁 沈阳 110034;2.辽宁装备制造职业技术学院 辽宁 沈阳 110161)
近年来,随着网络技术的飞速发展,无线传感器网络(Wireless sensor network,WSN)技术作为沟通物理世界与信息世界的桥梁,正日益引起学术界和工业界的重视。无线传感器网络监测技术融合了多个领域的先进技术[1]。无线传感器网络的研究与发展引起了学术界和工业界的广泛关注。在工业、农业、军事和民用等方面都有广泛的应用前景,是当前国际上备受关注的前沿热点研究领域[2]。目前已经在军事监控及环境治理、工业生产等多个行业获得广泛应用,随着应用的深入,WSN将会对社会的发展和人类的生活产生深远的影响。Sensor Network,LC-WSN)的应用,提出了能量优化路由算法。文献[4]研究了煤矿中实时定位和跟踪问题,表明井下采用RSS解决定位和跟踪问题的可行性。文献[5]的作者提出了集中式的多维定标定位算法,接着又提出了改进的分布式定位算法。本文提出了利用多维定标和扩展卡尔曼滤波相结合的节点定位方法,首先利用期望最大化算法获得初步结果,然后使用 SMCF算法 (Scaling by Major zing a Complicated Function)获得更加精确的解并采用矩阵变换将相对坐标转化为绝对坐标,最后利用扩展卡尔曼滤波对节点位置作进一步的精化。
1 相关研究
2 基于多维定标的节点定位方法
无线传感器网络定位的实质是根据已知确定位置的节点来确定未知节点的位置。多维定标是利用各对象之间的相异(似)性构造多维空间上点的相对坐标的一种技术。文献[3]研究了长链型无线传感器网络 (Long Chain-type Wireless
在研究中,选用的传感器节点自身具有RSS测量功能且随机部署,考虑一个由若干传感器节点和一个可移动的设备组成的应用场景,传感器节点随机部署于规定区域内,位置不变,称之为待定位节点。假设所有节点的物理特性相同,信号在两个节点之间传播产生的衰减与发送节点和接收节点无关,只与信号传播的距离有关。具体算法过程如下:
2.1 信号测量模型
接收节点收到的RSS值会随着与发射节点间的距离逐渐衰减,同时,信号传播环境中的噪音如散射、反射、折射等因素也会对信号产生很大影响。RSS值与距离不是确定关系,将它看作一个符合高斯分布的一个随机变量,使用如下对数正态分布模型。
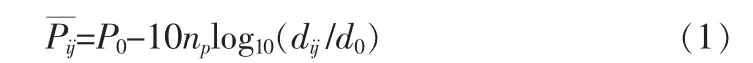
2.2 距离矩阵的建立
在获得任意两个节点之间的信号衰减后,通过式(1)计算任意两点之间距离,设X=|Xij|n×2表示n个节点在2维空间中的真实坐标,将任意两点间的距离用来dij(X)表示,则

2.3 期望最大化(EM)方法
期望最大化算法的目标是找到有隐含变量模型的最大似然估计解,算法由和两个步骤组成。在E步,使用当前参数值θold找到隐藏变量的后验分布。在M步,通过最大化联合分布函数的对数来确定修订的参数估计θnew。

2.4 SMCF 进一步求解
在求得节点的初步位置后,用多维定标技术来求解待定位节点坐标。该算法要求任意两个节点之间必须有确定的差异值,刚才求得的解可能不满足此条件。SMCF优化方法能够处理这种多维定标问题,SMCF算法通过优化复杂函数标度来构建收敛算法从而解决多维定标问题,该算法避免了通常降阶方法中需要求解微分和步长,可以解决很多其它求解多维定标算法运算过程的局限。将节点间的距离表示为:
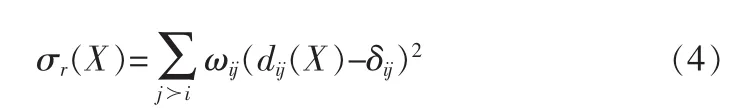
当获得 δij的值时,ωij设为 1,否则 ωij设为0。 这样我们对的定义范围是ωij≥0。任何X值,我们都可以对该表达式进行计算,称该式为胁强函数,对表达式做一些处理,有

胁强函数(5)是X的二次函数,通过使用迭代法进行求解。

2.5 权值调整方法
权值调整是定位中经常采用的方法,不但可以提高最终的定位精度,同时也可以有效减少运算时间。这里采用文献[9]建议的权值调整方法。
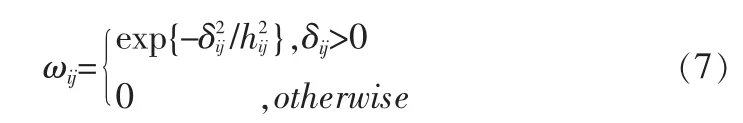
2.6 相对坐标到绝对坐标的变换
经过以上步骤之后,已经获得了节点的相对坐标,还需要进行坐标变换,将相对坐标转换成绝对坐标,也称为将局部坐标转换为全局坐标。如果已经获得3个节点的相对坐标和绝对坐标,则可以通过平移、旋转和镜像操作将未知节点的相对坐标转换为绝对坐标。从相对坐标到绝对坐标的平移变换用U0表示,旋转变换用U1表示,镜像变换用U2表示,因为我们考虑的是二维空间,这三个变换的表达式为
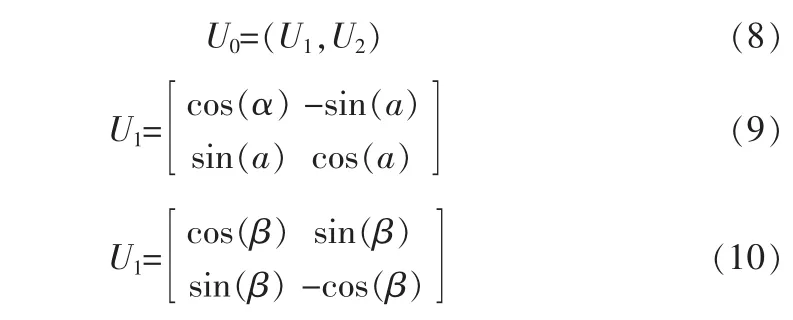
设已知三个节点的相对坐标和绝对坐标,并设其为X1,X2,X3,将旋转变换和镜像变换合并为一个未知量,令U=U1U2,得到U后,任意位置节点的绝对坐标都可以使用下面的变换获得。这样,所有未知节点的相对坐标全部转化为绝对坐标。
2.7 扩展卡尔曼滤波
在获得了基本的坐标之后,我们采用滤波做进一步的提纯。设状态方程和量测方程如下

εt是系统模型的噪声,δt是量测模型的噪声。为了使用卡尔曼滤波,需要对系统模型和量测模型中的函数求导,对函数g求一阶偏导,有
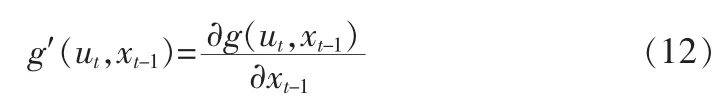
则扩展卡尔曼滤波的输入是(μt-1,∑t-1,ut,zt),输出是(μt,∑t),计算公式:
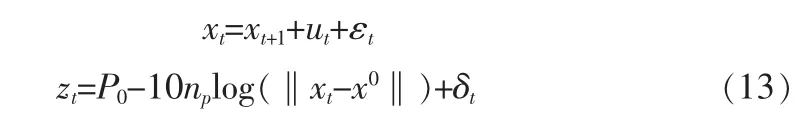
在获得导数之后,可以根据(15)逐步求解xt的值。在普通定位问题中,锚节点(也称为信标节点)位置不变,移动设备在运动过程中不断获得测量值,并通过滤波算法修正其自身的当前位置xt,当迭代结束后,最终的xt就是所求结果。在本问题中,移动节点位置一直变化,而待定节点的位置需要逐步修正。所以,需要对运算结果做一个调整,在一次滤波过程中,移动节点位置变化后,因为观测位置不变,通过将观测位置调整,保持它们位置的对应关系不变。
3 仿真结果及分析
仿真采用Matlab编程实现,算法比较时选择基本的多维定标方法算法[6]和修改权值的改进算法[7]进行比较,分别称为方法1和方法2。存在多种因素影响定位精度,例如移动节点初始位置估计、移动节点移动误差、节点个数等,本节对各种参数的影响进行分析。
因为 RSS的测量值是随机变量,为了减少随机性的影响,以下运行结果都是运行200次的平均值。同时因为随机变量的影响,随机的初始参数会有些差异,因此应该在相同的初始情况下,比较算法的定位精度。本文设置的基本仿真环境为的方形区域,节点采用均匀的随机部署方式,考虑3种分布:正方形、C型和L行。在对结果进行分析过程中,首先比较方法 1、方法 2和本文方法的直观定位结果,然后考虑不同参数对精度的影响。节点的真实位置和所求的近似位置之差的均方误差。因为每次结果运行200次且均方误差都大于0,所以最后的评价标准是这些RMSE的均值,如(14)(15)所示。
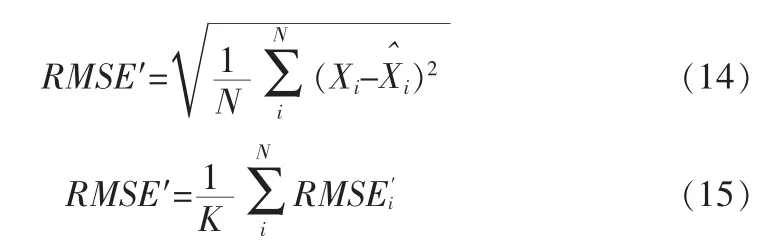
3.1 初始位置估计对定位精度的影响
下面考察EM求解初始值对定位精度的影响,以SVD求解的值为最佳结果,考虑在初步求解时存在一定的误差。如图1坐标表示存在的方差,从图中可以看出,方法1对初始值比较敏感,而方法2和本文方法对此不敏感,且影响都不大。不管方差如何,本文方法一直比法2的测量精度要高。
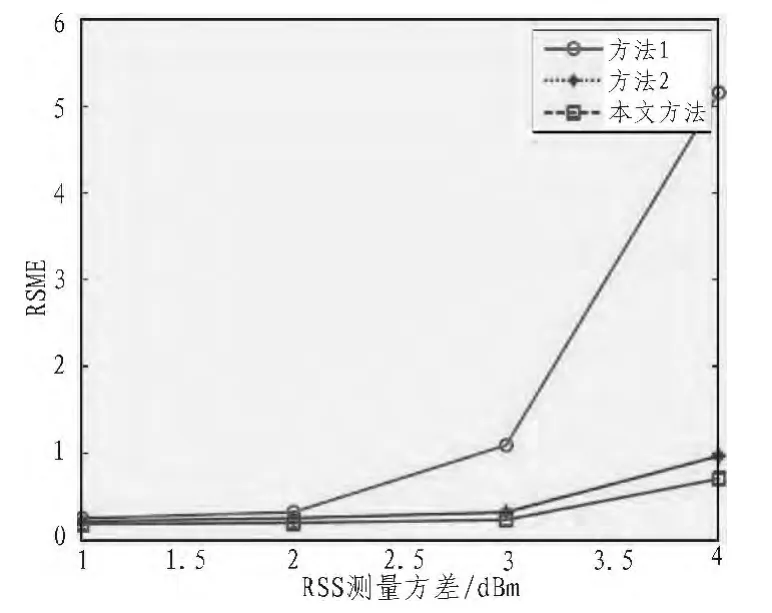
图1 EM迭代精度对定位的影响Fig.1 Effect ofmeasurement noise
3.2 移动节点定位误差对定位精度的影响
由于没有统一的全局坐标,在进行节点定位时,与移动节点的停留位置有关。移动距离的测量能力会影响定位精度,结果如图2示,方法1对定位误差承受能力不大,在方差从0.1变到2时,都有较大的RSME。而方法2和本文方法也都随着移动节点的定位精度降低产生了更大的定位误差,但是RSME变化不大,基本上在1以下,能够满足定位要求。
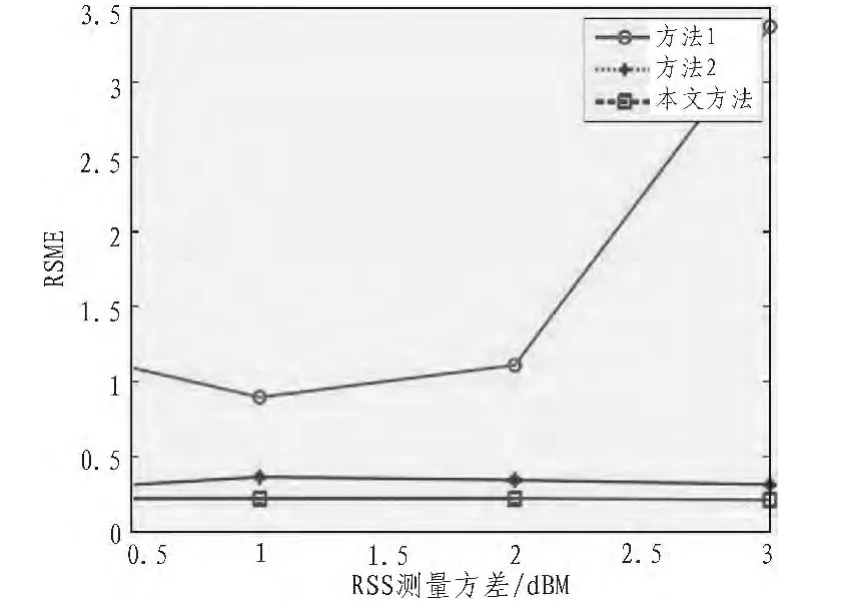
图2 动节点自身精度对定位的影响Fig.2 Effectof initial error of EM
3.3 节点数量对定位精度的影响
下面分析待定位节点数量与定位精度的关系,如图3示,节点数量增加会大大提高定位精度,方法1的提高尤为明显,当节点数从30增加到50时,定位精度提高了4倍。而方法2和本文方法也随着节点数量增加提高定位精度,但是程度并不明显,本文方法的RSME一直小于0.5,有较好的定位精度,本文方法在40个节点处定位精度高于方法2有60个节点时的定位精度,表明本文方法定位精度更高。
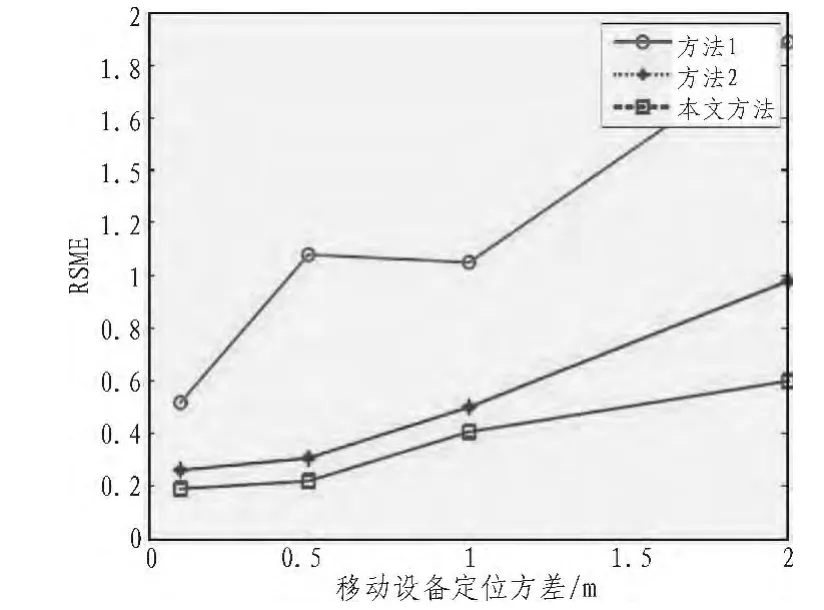
图3 点个数对定位精度的影响Fig.3 Effect of localization ofmobile node
4 结束语
研究首先分析了无锚节点定位的基本算法和常见的多维定标算法,对于没有锚节点提供全局坐标,以移动节点自身为坐标系建立绝对坐标,并考虑其自身位置误差;在考虑移动节点有效利用方面,在改进的多维定标算法的基础上,增加扩展卡尔曼滤波过程,提高了定位精度。详细分析算法的组成结构并给出算法步骤后,讨论了正方形场景、C型场景和L型场景的随机均匀部署的情况,分析了定位精度以及多种不同的参数设置对算法的影响,并通过实际测量数据,验证该算法对定位精度能有效的提高。
[1]高建良,徐勇军,李晓维.基于加权中值的分布式传感器故障检测[J].软件学报,2007,18 (5):1208-1217.GAO Jian-liang,XU Yong-jun,LI Xiao-wei.Weigh ted median based distributed fault detection for wireless sensor networks[J].Journal of Software,2007,18(5):1208-1217.
[2]闫丹,雷霖.基于免疫神经网络的无线传感器网络节点的故障诊断[J].自动化信息,2009,95(3):37-39.YAN Dan,LEILin.Fault diagnosis of nodes in wireless sensor network based on immune neural network[J].Automation Information,2009,95(3):37-39.
[3]苏金树,胡乔林,赵宝康.容延容断网络路由技术[J].软件学报,2010,21(1):119-132.SU Jin-shu,HU Qiao-lin,ZHAO Bao-kang.Routing techniques on delay/disruption tolerant networks[J].Journal of Software,2010,21(1):119-132.
[4]刘影,钱志鸿,刘丹,等.基于几何学的无线传感器网络定位算法[J].光电子激光,2010,10(21):1435-1438.LIU Ying,QIAN Zhi-hong,LIU Dan,et al.A wireless sensor network localization algorithm based on geometry[J].Journal of Optoelectronics.Laser,2010,10(21):1435-1438.
[5]谢涛.无线传感器网络中DV-Hop算法的改进[D].西南大学,2012.
[6]Perspective MLAP.Machine Learning:A Probabilistic Perspective[J].The MITPress,2012:348-352.
[7]Chang C,Lin C,Hsieh C,et al.Patrolling Mechanisms for Disconnected Targets in Wireless Mobile Data Mules Networks: Parallel Processing (ICPP) [C], 2011 International Conference on,2011:3-98.
[8]黄旭红.无线传感器网络节点节能管理方式的研究[J].现代电子技术,2011(15):32-34,38.HUANG Xu-hong.Wireless sensor network node power conservation management practices[J].Modern Electronics Technique,2011(15):32-34,38.

