贴边岔管设计探讨

吴 均

(新疆水利水电勘测设计研究院,乌鲁木齐 830000)

文章编号：1006—2610(2015)03—0077—03

贴边岔管设计探讨

吴 均

(新疆水利水电勘测设计研究院,乌鲁木齐 830000)

对于大型贴边岔管设计宜采用有限元法计算，但对于中、小型贴边岔管设计可采用面积补偿法、圆环法等结构分析方法计算。文章结合工程实例，对中、小型贴边岔管设计采用几种结构分析方法进行计算对比，并用有限元法对计算结果进行验证。结果表明，采用面积补偿法、圆环法等结构分析方法计算结果与有限元计算结果是一致的。

水电站;贴边岔管;结构分析;有限元

0 前 言

新疆某水电站工程主要任务是发电和发电反调节，工程装机规模为100 MW(2×35 MW+2×15 MW)，采用大小机。引水隧洞采用一洞四机的供水方式，岔管采用对称Y型岔，其中钢衬段主管直径为6.2 m，支管直径为3.4 m(大机)和2.4 m(小机)。

在施工阶段，业主提出为满足工程管理区和下游林地的用水要求，工程建成后需要从压力管道(钢衬钢管段)上开孔取水。经计算，取水口管管径为400 mm，对应的取水口直径也选为400 mm。此时，压力钢管已经制作安装完成，经综合考虑，取水管与已制作安装完成的钢管宜采用贴边岔管形式。由于受交通及其他建筑物布置限制，最终取水口布置在压力钢管主管段上。

1 贴边岔管结构分析计算方法

目前，贴边岔管计算方法较多，本文结合新疆某水电站工程贴边岔管设计实例，对中、小型工程贴边岔管设计计算常用的面积补偿法、圆环法等结构分析方法进行了对比，并用有限元对计算结果进行了验算[1-6]。

该水电站工程贴边岔管主管直径6.2 m，取水管直径0.4 m，岔管处设计水头为120 m(含水击压力)，主管壁厚为26 mm。由于该取水管垂直于主管布置，取分岔角为90°。主管及取水管管材均为Q345R钢。

1.2 面积补偿法

面积补偿法在中、小型贴边岔管设计中是一种应用较广的方法。面积补偿法是在管道破口处增加补强板，确定补强板尺寸时沿主管轴线的纵剖面，在主管的破口处补强板截面积Ad不小于主管破口截面积Ae；补强板厚度td为主管壁厚t的1.0～1.3倍，如图1所示。

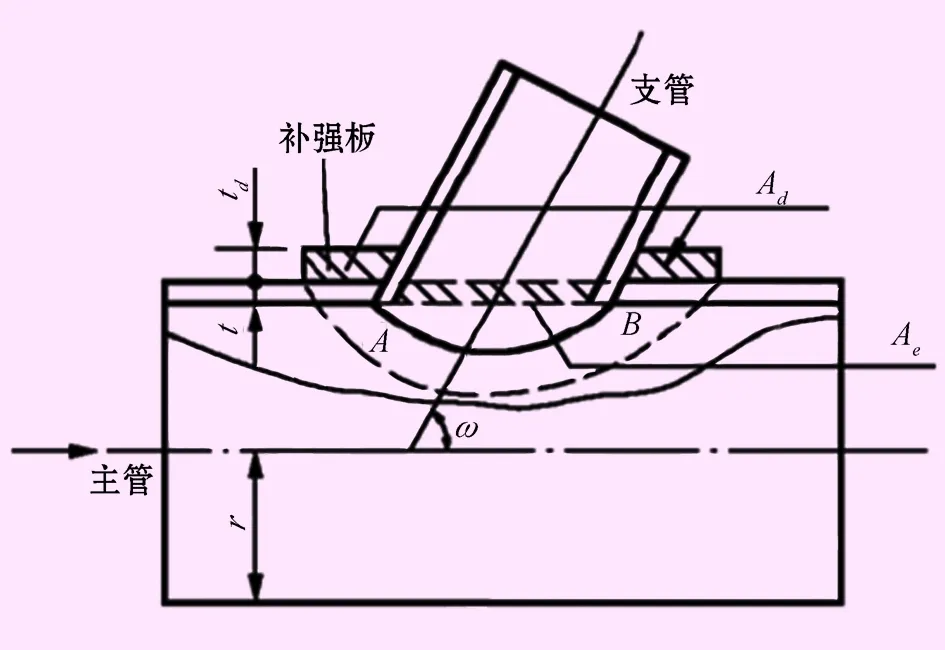
图1 面积补偿法计算结构示意图

依据补强板尺寸确定方法，可事先初拟补强板的尺寸，再根据以下经验公式，计算贴边岔管锐角贴边外缘最大主应力值。

(1)

(2)

式中：t为主管壁厚,取26 mm；p为内水压力设计值,N/mm2；d、D分别为支、主管轴线交点处的直径,取400 mm和6 200 mm；α2、α1分别为支、主管半锥顶角,均都取为0°；β为分岔角,取90°；σ0为主管膜应力,N/mm2；σ为孔口局部应力,N/mm2。

初步拟定补强板尺寸：宽为300 mm，厚度与主管壁厚一致，均为26 mm，材质与主管同。经计算，补强后主管最大膜应力为157.5 MPa，锐角贴边外缘最大主应力为73.9 MPa，都小于钢材极限抗力限值187.5 MPa。其中主管最大膜应力接近钢材极限抗力限值，材料得到了比较充分的利用，说明初步拟定的补强板尺寸是比较合理的。

1.3 圆环法

在临床治疗中,妇科腹腔镜手术是首选的手术治疗方法。妇科腹腔镜手术方法具体众多优点,如手术安全性高、手术中出血量小、手术后恢复快等,从而有利于患者术后康复。但是妇科腹腔镜手术效果与麻醉技术有着密切关系,因此在实施腹腔镜手术过程中,麻醉至关重要[2][3]。

圆环法也是中、小型贴边岔管设计中一种应用较广的方法，其计算简图如图2所示。

图2 圆环法计算结构示意图

圆环法计算原则是把补强板当作一圆环加劲结构，竖向荷载pr为主管破口处的不平衡力，横向荷载则为主管管壁对补强板变形产生的约束力。

在确定管壁破口处应力时，需要先明确管壁破口处最大弯矩和最大拉应力。 管壁破口处最大弯矩和最大拉应力可依据下列公式计算：

(3)

N=prrd

(4)

管壁破口处环向应力可依据下列公式计算：

(5)

(6)

式中:M为弯矩,N·mm;N为轴拉力,N；r为主管半径,取3 100 mm;rd为圆环中心半径,取350 mm；p为内水压力设计值,N/mm2;σ1、σ2分别为环向应力,N/mm2；A为补强板加劲结构有效截面积,mm2；Z为补强板有效截面上计算点至重心轴的距离,mm；I为补强板有效截面对重心的惯性矩,mm4。

用圆环法计算时，补强板尺寸采用经面积补偿法计算后确定的补强板尺寸。即补强板宽为300 mm，厚度与主管壁厚一致，均为26 mm，材质与主管同。经计算，补强后管壁破口处的最大应力为172.2 MPa，小于钢材极限抗力限值187.5 MPa，说明初步拟定的补强板尺寸是比较合理的。

1.4 人孔补强法

为了便于对压力钢管进行检修及维护，在较长的压力钢管上经常会留有进人孔。在进人孔颈管与主管衔接处，也会在主管破口处采用补强板进行补强。人孔补强法主要是参照钢管进人孔设计方法，人孔补强法适用于下列条件的孔口。

(1) 钢管内径D≤1 500 mm，开孔允许的最大直径d≤1/2D；同时d不允许超过500 mm。

(2) 钢管内径D>1 500 mm，开孔允许的最大直径d≤1/3D；同时d不允许超过1 000 mm。

本文所例水电站主管内径D=6 200 mm，开孔处直径d=400 mm，d≤1/3D，进水管轴线与钢管主管轴线垂直，也可用进人孔设计方法进行计算。

补强板焊接在孔周管壳外缘，板面弯曲，曲率同钢管外壳，内缘与颈管外壁焊接。当补强板采用厚度与管壁相同时补强板外径D2由下式决定：

(7)

(8)

式中：D2为补强板外径，mm；Dk为支管内径,mm；其余符号意义同前式。

补强板壁厚和主管壁厚一致，均为26 mm，经计算，补强板外径D2约为677 mm，小于用面积补偿法和圆环法计算确定的补强板外径D2(1 000 mm)。所以，补强板尺寸最终用面积补偿法和圆环法计算确定。

确定补强板外径D2后，可按下式初步判断拟定的D2及t1能否满足要求。

(9)

式中：t1为补强板厚度,mm；t2为支管壁厚，取8 mm；φ为焊缝系数，取0.9；其余符号意义同前式。

经计算，式(9)不等式左边数值为16 061 mm2，右边数值为10 608 mm2，左边大于右边，满足不等式。可见补强板尺寸选取是合适的。

2 计算结果验证

针对上述结构分析法确定的补强板厚度及宽度，用有限元法进行复核验算。计算模型长度为主管直径的1.5倍(以岔管中心为起点向上游或者向下游计算)，边界条件采用全约束(即水平竖向位移和转角)，网格划分采用四边形结构化网格，为提高计算精度，在岔管补强处对网格进行了局部加密。计算模型网格划分及应力云图如图3、4所示。

从图4知，岔管贴边补强处最大主应力为169.1 MPa，小于钢材极限抗力限值187.5 MPa，说明通过结构析方法所选取的补强板厚度和宽度是合适的。

3 结 语

(1) 贴边岔管设计几种结构分析计算方法的计算结果和有限元计算结果可以看出，在取上述补强板宽度和厚度的情况下，主管破口处应力、贴边外缘最大主应力、主管膜应力、贴边补强处最大主应力均接近但小于钢材极限抗力值，说明通过结构分析法确定的补强板结构尺寸取值是比较合理的。

图3 计算模型网格划分图

图4 计算模型应力云图

(2) 对中、小型工程，在设计贴边岔管时，采用结构分析法确定补强板的厚度及宽度是可行的。

[1] DL/T 5141-2001,水电站压力钢管设计规范[S].北京：中国电力版社，2001.

[2] SL 281-2003,水电站压力钢管设计规范[S].北京：中国水利水电出版社，2003.

[3] 王巧红,李文召.嵊州引水工程贴边岔管方案的有限元计算[J].浙江水利水电专科学校学报,15(2):35-37.

[4] 荣誉,陈洁.岳城水库供水工程贴边岔管设计[J].水利水电工程设计,1999，(3):7-8.

[5] 水电部水利水电规划设计院.水电站机电设计手册(金属结构)[M].北京：水利电力出版社，1991.

[6] 黄希元,唐怡生.小型水电站机电设计手册[M].北京：水利电力出版社，1989.

Study on Design of Welted Bifurcated Penstock

WU Jun

(Xinjiang Water Resources and Hydropower Investigation Design and Research Institute, Urumqi 830000,China)

The finite element method is applied for design of large-scaled welted bifurcated penstock. For small and medium-sized welted bifurcated penstocks, the structural analysis methods such as area compensation method, ring method and etc can be applied for calculation. In combination of engineering practice, several structural analyzing methods for design of small/medium-sized bifurcated penstocks are compared. The corresponding results are verified by results by the finite element method. The comparison presents that the results by area compensation method, ring method, etc are in compliance with those by the finite element method.

hydropower station; welted bifurcated penstock; structural analysis; finite element

2015-03-19

吴均(1979- ),男,四川省遂宁市人，工程师，从事水工设计研究工作.

TV674

A

10.3969/j.issn.1006-2610.2015.03.022