不同断面形状对人工渠道糙率影响的试验研究

赵锦程

(新疆水利水电勘测设计研究院,乌鲁木齐 830000)

文章编号：1006—2610(2015)02—0079—03

不同断面形状对人工渠道糙率影响的试验研究

赵锦程

(新疆水利水电勘测设计研究院,乌鲁木齐 830000)

为探究不同断面对渠道糙率的影响，采用2种不同断面的人工渠道，在2种底坡及5种不同流量的条件下研究糙率随流量、底坡的变化规律。试验结果表明：在明渠均匀流条件下，在相同底坡、不同断面的人工渠道中，糙率的变化与流态有关，当Fr<1时，糙率值随着流量的增大逐渐减小；当Fr>1时，糙率值随着流量的增大逐渐增大。人工渠道断面形状发生变化时，糙率与各水力要素之间关系的变化规律基本相同，渠道的断面形状并不是影响渠道糙率变化的因素之一。

人工渠道；糙率；底坡；断面形状；试验研究

0 前 言

明渠水流广泛地存在于自然界中，明渠水流的水力计算是水利工程计算中一个重要组成部分，而糙率是水力计算中的重要敏感参数，受众多因素的影响，要准确选用和标定糙率绝非易事，如若确定不准往往会给求解计算带来很大的误差。长期以来，人们对糙率系数的研究从未停止过，对糙率系数的特性以及它与一些水力要素相关关系也有了一定的认识[1-5]。马吉明等[6]对南水北调中线工程的宽浅渠道进行模型试验，认为对于水力半径较大、断面形状和尺寸一定的渠道来说，糙率将随流量的加大而加大。而杨岑等[7]采用3种不同粗糙度的人工加糙矩形渠道进行试验，得出同一粗糙度的明渠糙率随流量的增加呈对数减小的趋势。二者所得结论完全相反。由此可以看出，对于影响糙率变化的因素目前还没有定论。

笔者在总结前人研究成果的基础上，试验分析了在不同断面形状的条件下，明渠均匀流糙率随流量弗汝德数及水深的变化的规律。为进一步研究糙率的特性以及选取、修正水力计算中糙率提供依据。

1 试验布置及方案

1.1 试验布置

本试验研究在新疆农业大学水利与土木工程学院水力学实验室进行，分别制作了长10 m，宽0.36 m，深0.29 m的PVC板矩形渠道和渠道底宽0.2 m，渠深0.17 m，边坡系数m=1，渠长10 m的PVC板梯形渠道，试验布置矩形渠道与梯形渠道基本一致，底板下放置钢梁以便于后期调整渠道坡度。试验系统包括：泵房、供水管道、调节阀门、三角形量水堰、矩形量水堰、水箱、地下回水渠道。为了获得试验所需要的明渠均匀流，在渠道前端安设水箱，用以稳定水流，当固定流量条件下的上下游水位一致时，便形成了明渠恒定流。试验中取渠道中间均匀流段为量测对象。试验系统见图1。

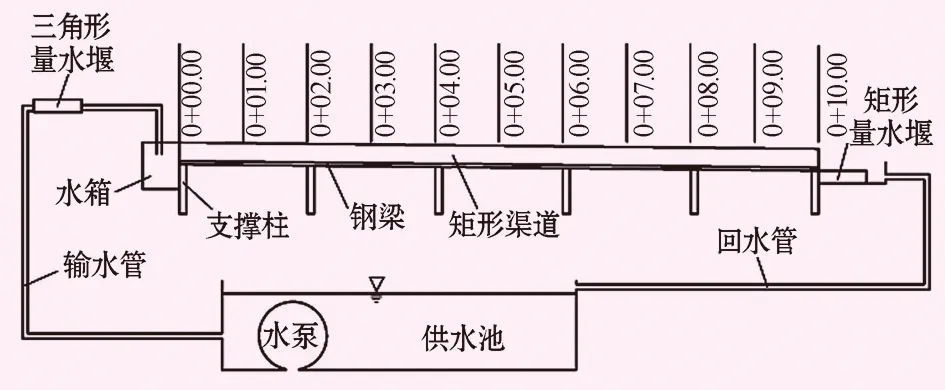
图1 试验系统图 单位：m

1.2 试验方案

如图1所示，取0+03.0 m、0+05.0 m、0+07.0 m处作为测量水深的断面。使用水位测针对水深进行量测。每个测量断面分别布置左、中、右3个测点。其中左右测点距离边壁5 cm，中点为断面的中点，距离两侧边壁10 cm，计算时采用左中右3点的均值。选取0.001、0.03共2种不同的底坡进行试验。试验中通过流量调节阀门和上下游量水堰控制流量大小及其精度。每种底坡下均选取5组流量，试验流量的变化范围为13～28 L/s，流量调节幅度为3 L/s。因此试验共进行了5×4=20组。

2 试验结果及分析

2.1 相同底坡下流量Q与糙率的关系

利用明渠均匀流的公式：

(1)

和曼宁公式：

(2)

得出：

(3)

式中：n为糙率；A为过水断面面积,m2；R为断面的水力半径,m；i为渠道底坡；Q为渠道过水流量,m3/s；C为谢才系数。

试验中分别量测出不同底坡所对应的流量、水深,然后利用式(3)计算不同底坡、不同流量、不同断面形状所对应的糙率值,计算结果见表1。

表1 相同底坡不同断面的Q-n值表

根据表1绘制出相同坡度下不同断面Q-n关系曲线，见图2、3。

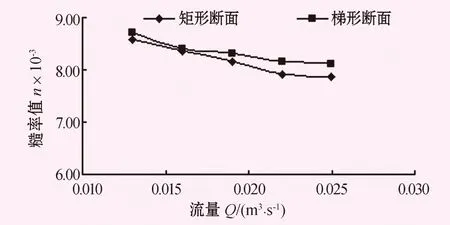
图2 底坡i=0.001时Q-n关系图

图3 底坡i=0.03时Q-n关系图

由表1和图2、3可知，当底坡i=0.001，渠道断面为矩形时，随着流量的增大糙率值逐渐减小；渠道断面为梯形时，随着流量的增大糙率值也逐渐减小。当底坡i=0.03，渠道断面为矩形时，随着流量的增大糙率值逐渐增大；渠道断面为梯形时，随着流量的增大糙率值逐渐增大。

2.2 相同底坡弗汝德数Fr与糙率关系

利用公式：

(4)

计算出不同底坡渠道中不同流量水深所对应的弗如德数Fr。

式中：α为动能修正系数，一般取α=1.0；v为断面平均流速，m/s；g为重力加速度，取9.81 m/s2；h为断面平均水深，m。

由表1及公式(4)可得不同底坡、不同流量、不同断面所对应的弗汝德数和糙率值的关系，计算结果见表2。

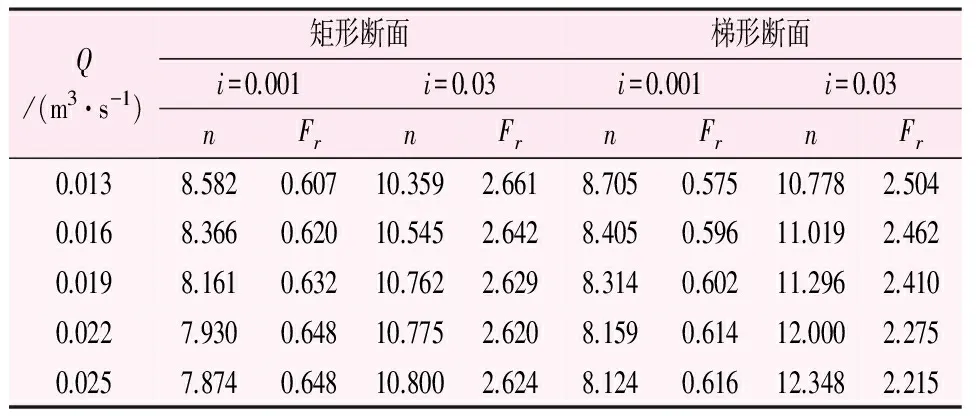
表2 相同底坡不同断面的Fr-n值表

根据表1绘制出相同坡度下不同断面Fr-n关系曲线，见图4、5。

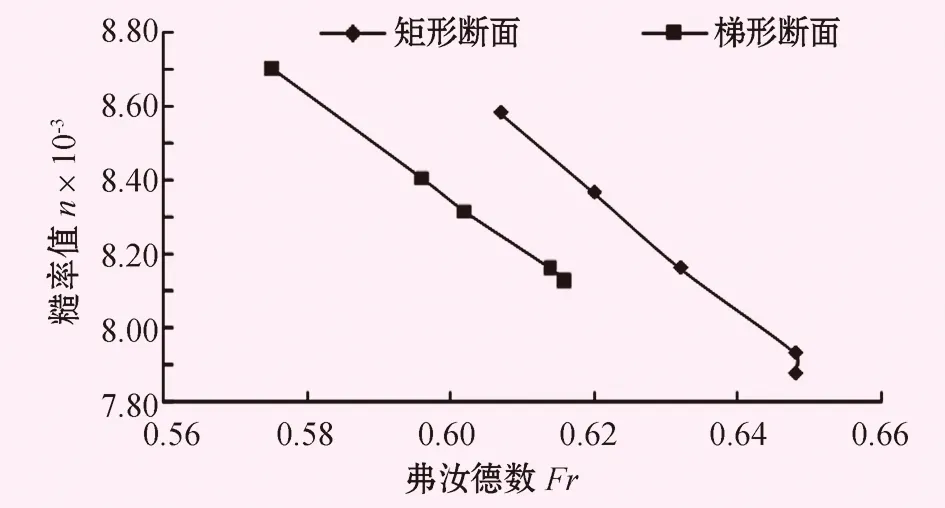
图4 底坡i=0.001时Fr-n关系图

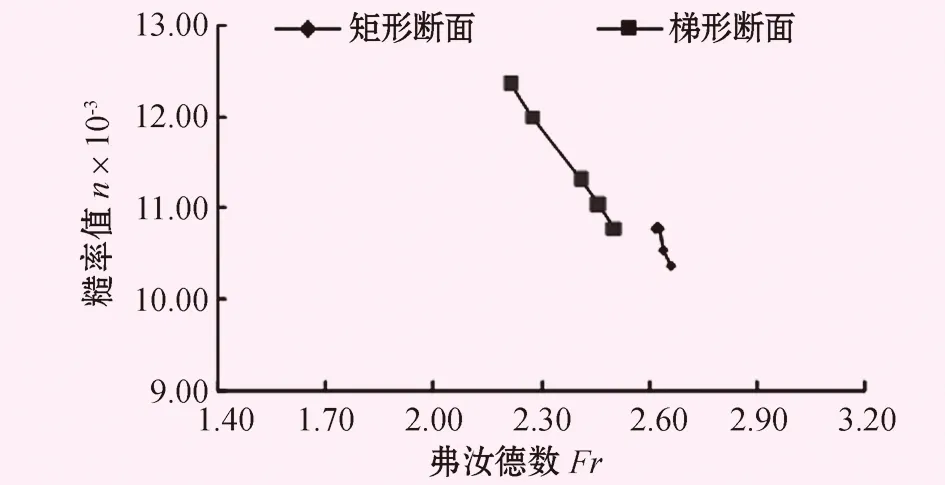
图5 底坡i=0.03时Fr-n关系图

由表2和图4、5可知，当底坡i=0.001，渠道断面为矩形时，随着弗汝德数Fr的增大糙率值逐渐减小；渠道断面为梯形时，随着弗汝德数Fr的增大糙率值也逐渐减小。当底坡i=0.03，渠道断面为矩形时，随着弗汝德数Fr的增大糙率值逐渐减小；渠道断面为梯形时，随着弗汝德数Fr的增大糙率值也逐渐减小。同时，还可以看出当Fr<1时，随着流量的增大糙率值逐渐减小；当Fr>1时，随着流量的增大糙率值逐渐增大。

2.3 相同底坡水深h与糙率关系

通过水位测针可测得矩形断面与梯形断面在相同底坡下，不同流量所对应的水深，水深h为同一断面左、中、右3个测点的均值，计算结果见表3。

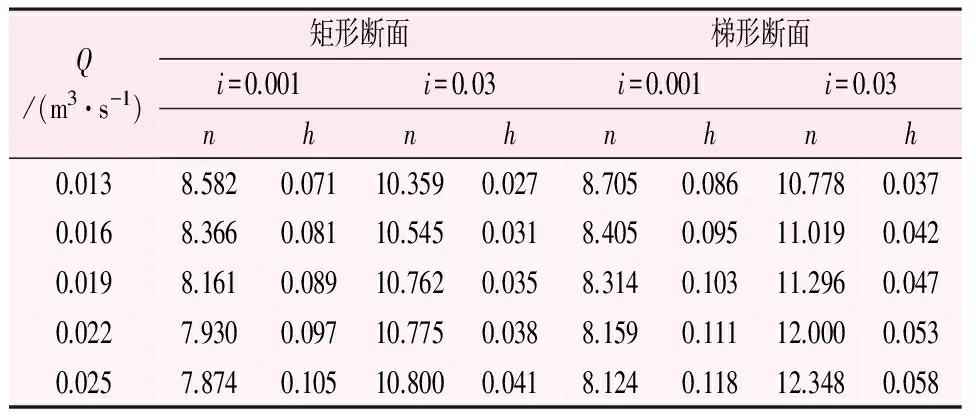
表3 相同底坡不同断面的h-n值表

根据表3绘制出相同坡度下不同断面h-n关系曲线，见图6、7。

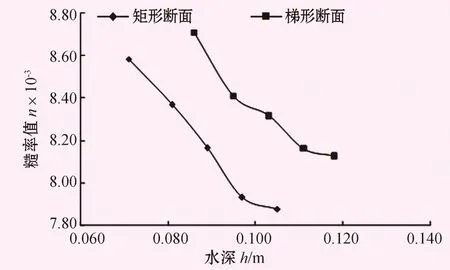
图6 底坡i=0.001时h-n关系图

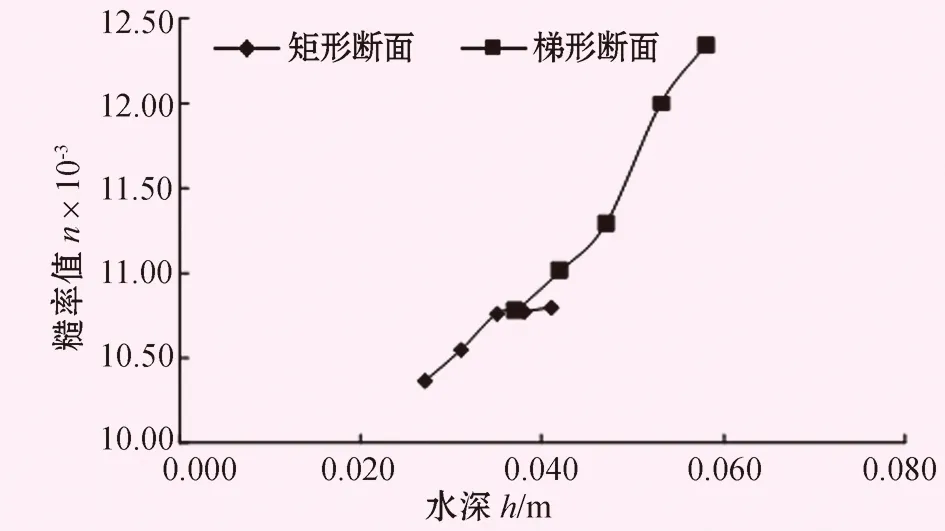
图7 底坡i=0.03时h-n关系图

由表3和图6、7可知，当底坡i=0.001，渠道断面为矩形时，随着水深的增大糙率值逐渐减小；渠道断面为梯形时，随着水深的增大糙率值也逐渐减小。当底坡i=0.03，渠道断面为矩形时，随着水深的增大糙率值逐渐增大；渠道断面为梯形时，随着水深的增大糙率值也逐渐增大。

3 结 语

通过对不同底坡不同断面的人工渠道进行试验研究，得出以下几点结论：

(1) 在相同底坡下，不同断面形状的人工渠道中，糙率值随流量的变化关系与流态有关。缓流中，糙率值随着流量的增大而减小；急流中，糙率值随流量的增大而增大。

(2) 在相同底坡下，不同断面形状的人工渠道中，糙率与各种水力要素之间关系的变化规律基本相同，因此，渠道的断面形状并不是渠道糙率变化的影响因素之一。

[1] 李榕.关于影响曼宁粗糙系数n值的水力因素探讨[J].水利学报,1989,(12)：62-66.

[2] 董槐三,陈耀忠.引滦入津隧洞糙率的原型观测[J].水力发电,1987,(03)：46-52.

[3] 曾祥,黄国兵,段文刚.混凝土渠道糙率调研综述[J].长江科学院院报,1999,(06)：1-4.

[4] 何建京,王惠民.流动型态对曼宁糙率系数的影响研究[J].水文,2002,(06)：22-24，53.

[5] 李丽,王加虎,王建群,等.自适应随机搜索算法在河网数学模型糙率反演中的应用[J].水利水电科技进展,2011,31 ( 5 ): 64-67.

[6] 马吉明，史哲.南水北调典型宽浅渠道糙率系数研究[J].水力发电学报,2007,(05)：75-79.

[7] 杨岑,路泽生,栾维功,李建雄,吕宏兴,张宽地.矩形渠道人工加糙壁面阻力规律试验研究[J].长江科学院院报,2011,(01)：34-38.

Study on Tests of Roughness of Artificial Canal With Different Sections

ZHAO Jin-cheng

(Xinjiang Water Resources and Hydropower Investigation Design and Research Institute, Urumqi 830000，China)

To study the roughness of the artificial canal with different sections, the artificial canal with two different sections are applied to study the law of the roughness with variation of discharge and bottom slope at the conditions of two bottom slopes and five different discharges. The tests present that, in conditions of uniform flow in open canal, roughness varies with flow pattern in the artificial canal with same bottom slope and different section. WhenFr<1, the roughness increases with the discharge decrease; whenFr>1, the roughness increases with the discharge increase. When the canal section changes, the variation law of the relationship between roughness and hydraulic factors is the same basically. The section shape of the canal is not the factor which impacts the roughness variation.

artificial canal; roughness; slope bottom; section shape; study on test

2014-09-20

赵锦程(1986- ),男,西安市人,助理工程师,主要从事水利工程设计工作.

新疆水利水电工程重点学科基金(xjslgczdxk20101202).

TV135.3

A

10.3969/j.issn.1006-2610.2015.02.020