The Nonlinear Bifurcation and Chaos of Coupled Heave and Pitch Motions of a Truss Spar Platform

HUANG Lei, LIU Liqin, LIU Chunyuan, and TANG Yougang

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

The Nonlinear Bifurcation and Chaos of Coupled Heave and Pitch Motions of a Truss Spar Platform

HUANG Lei, LIU Liqin*, LIU Chunyuan, and TANG Yougang

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

This paper presents the results from a numerical study on the nonlinear dynamic behaviors including bifurcation and chaos of a truss spar platform. In view of the mutual influences between the heave and the pitch modes, the coupled heave and pitch motion equations of the spar platform hull were established in the regular waves. In order to analyze the nonlinear motions of the platform, three-dimensional maximum Lyapunov exponent graphs and the bifurcation graphs were constructed, the Poincaré maps and the power spectrums of the platform response were calculated. It was found that the platform motions are sensitive to wave frequency. With changing wave frequency, the platform undergoes complicated nonlinear motions, including 1/2 sub-harmonic motion, quasi-periodic motion and chaotic motion. When the wave frequency approaches the natural frequency of the heave mode of the platform, the platform moves with quasi-periodic motion and chaotic motional ternately. For a certain range of wave frequencies, the platform moves with totally chaotic motion. The range of wave frequencies which leads to chaotic motion of the platform increases with increasing wave height. The three-dimensional maximum Lyapunov exponent graphs and the bifurcation graphs reveal the nonlinear motions of the spar platform under different wave conditions.

truss spar platform; coupled heave and pitch; quasi-periodic motion; chaotic motion; 1/2 sub-harmonic motion; maximum Lyapunov exponent; bifurcation graph

1 Introduction

The spar platform is one of the most important platform types in deep-sea oil and gas field. Research on spar platform mainly focuses on wave loads acting on the hull and the hydrodynamic characteristics, dynamic response of the platform, the mooring system and the riser system, and the vortex-induced vibration of the platform (Tang, 2008). With the increase of operation water depth, a greater accuracy on predicting the motions of the spar platforms is required. The platform motions were studied considering coupling between the hull, mooring system and riser system, and the coupling of different degree of freedoms were also performed (Tahar and Kim, 2008; Jameel et al., 2011; Yang et al., 2012; Xu and Jing, 2013).

Due to the large draft, the natural periods of the spar platform are relatively long, and the ratio between the natural frequencies of the heave mode and the pitch mode is close to 2:1. Under the excitation of long period wave or ground swell, the spar platform undergoes complicated nonlinear motions, such as response jumping, Mathieu instable motion, super-harmonic and sub-harmonic bifurcation. Haslum and Faltinsen (2000) studied the pitch motions of a spar platform using model experiment. Theyplotted the Mathieu stable graphs of the pitch motion. Rho and Choi (2004) established the pitch motion equation of a truss spar platform and investigated the stability. They found that large amplitude motion of the heave may lead to unstable pitch motions. The response jumping occurs when the wave frequency is close to the natural frequency of heave mode of the platform. Lim et al. (2005) studied the coupled heave and pitch motions of a cell spar platform experimentally. They observed that pitch motion becomes unstable when kinetic energy from the heave mode is transferred to the pitch mode due to coupling. Zhao et al. (2010) studied the nonlinear coupled motions of heave and pitch of a classic spar platform with2:1 internal resonance between the heave and the pitch modes. The parameter domain that leads to unstable response was also calculated. Gavassoni et al. (2014) studied the dynamic responses of coupled heave and pitch motions of a truss spar platform analytically. The Floquet theory, the bifurcation diagrams and Mathieu charts were used to analyze the instable motions of the platform. Some important response features were obtained, such as response jumping, bifurcation and unstable solutions. The results also showed that damping is essential to control the large amplitude response.

Using a numerical method, the present research studied the bifurcation and chaotic motions of a truss spar platform in regular waves. The nonlinear methods of maxi-mum Lyapunov exponent, bifurcation graphs and Poincaré maps were used to investigate the response of the truss spar platform.

2 Coupled Motion Equations of Heave and Pitch of the Truss Spar Platform

For simplicity, the current study does not include the coupling motions between surge and pitch. Yan (2010) analyzed the effects of surge motion on the nonlinear coupled heave-pitch motions of a cylinder structure. She found that the existence of the surge motion did not affect the frequency condition for instable heave-pitch coupling motions. This is because the natural frequencies of the system do not vary with surge motion. However, for certain situations with certain initial conditions, she found that the effect of interactions between surge motion and base flow may strengthen or weaken the growth of unstable heave and pitch motions.

The coupled motion equations were established based on the work of Rho and Choi (2004), Zhao (2010), Shen and Tang (2011). Considering the restoring force (moment), linear damping force (moment), quadratic damping force (moment) and the regular wave exciting force (moment), the heave-pitch coupling motion equations of the platform hull can be written as

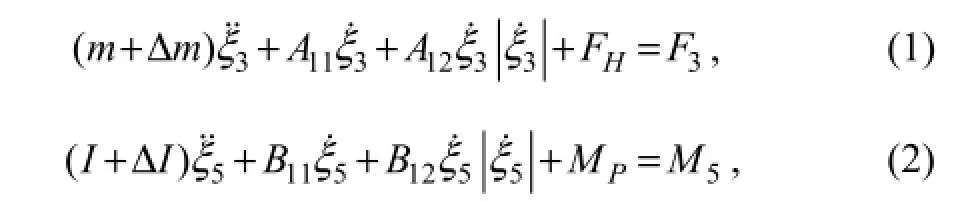
where ξ3(t) is the heave displacement, ξ5(t) is the pitch angle, m is the hull mass, Δm is the heave added mass, I is the moment of inertia of pitch, ΔI is the added moment of inertia of pitch A11is the linear damping coefficient of the platform heave, A12is the quadratic damping coefficient of the platform heave, B11is the linear damping coefficient of the platform pitch, B12is the quadratic damping coefficient of the platform pitch, FHis the restoring force of the platform heave, MPis the restoring moment of the platform pitch, F3and M5are wave force acting on the platform heave and wave moment acting on the platform pitch.

Considering mutual influences between the heave mode and the pitch mode, the heave restoring force of the platform hull in calm water is (Zhao, 2010)

where ρ is the water density, g is the acceleration of gravity, Awis area of the water plane of platform hull, Hgis the vertical distance from calm water surface to the center of gravity of the platform, η(t) is the wave elevation.

The pitching restoring moment is

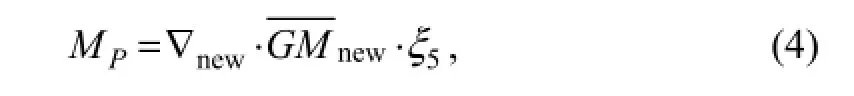
where ∇newis the instantaneous volume of displacement, GMnewis the instantaneous meta center height, they can be written as follows (Zhao, 2010)

where ∇ is the initial volume of displacement of the platform,GM is initial meta centric height of the pitch.

Assuming ξ5is a small angle, according to the Taylor expansion, the following formula can be obtained

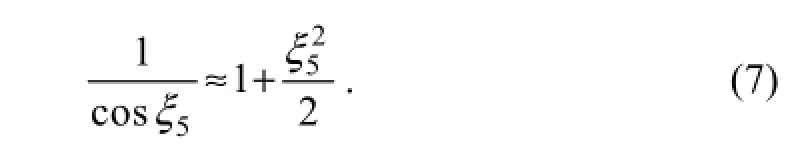
By ignoring the effect of wave elevation and the higher order nonlinear terms (higher than 2nd order), substituting Eq. (7) into Eq. (3), Eq. (5) and Eq. (6), Eq. (3) and Eq. (4) can be rewritten as

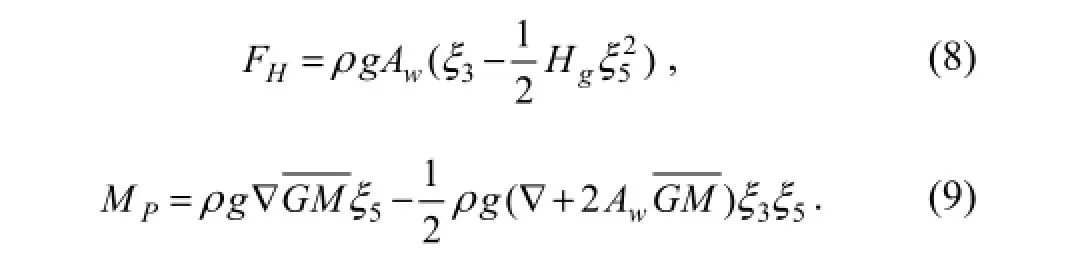
Substituting Eq. (8) and Eq. (9) into Eq. (1) and Eq. (2), and then dividing Eq. (1) and Eq. (2) by (m+Δm) and (I+ ΔI), respectively, yields the relations

where

Eq. (10) and Eq. (11) show that heave and pitch of the spar platform are coupled by nonlinear terms.

3 Wave Force (Moment) Acting on the Platform

The first order wave force and wave moment are onlyconsidered here. Following Weggel and Roesset (1994), the total heave force acting on the hull was assumed to be the product of a diffraction coefficient and the Froude-Krylov force (Sadeghi et al., 2004), where the Froude-Krylov force acting on the bottom of a truncated cylinder can be written as

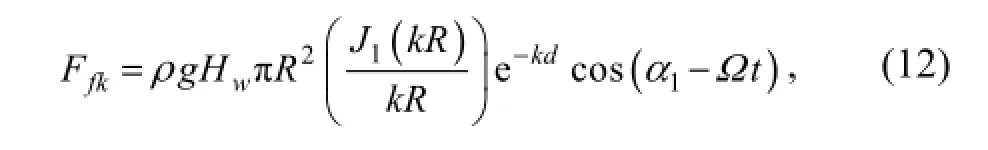
where Hwis the wave height, k is the wave number, R is radius of the platform hull, J1is the first order Bessel function of first kind, d is draft of the platform hull, Ω is the wave frequency,. Then the heave force acting on the spar hull can be written as (Sadeghi et al., 2004)

The pitching moment acting on the hull can be approximated using the linear diffraction theory. The first order surge wave force acting on the unit length of a vertical cylinder can be written as (Zhao, 2010)

4 The Lyapunov Exponent

The Lyapunov exponent is one of the most popular tools to investigate the stability and chaos of nonlinear dynamic system. It denotes the average exponent divergence or convergence rate of the neighboring trajectories in the phase space (Wolf et al., 1985). The negative exponent denotes periodic motion and the positive exponent denotes a periodic motion. In this study, the maximum Lyapunov exponents were used to assess the chaotic motion of the truss spar platform. They were calculated using the Wolf’s QR decomposition method (Andrea and Gallas Jason, 1995), which is based on the growth of tangent vectors in the phase space of the dynamical equations.

Eq. (10) and Eq. (11) are transformed into following differential equations

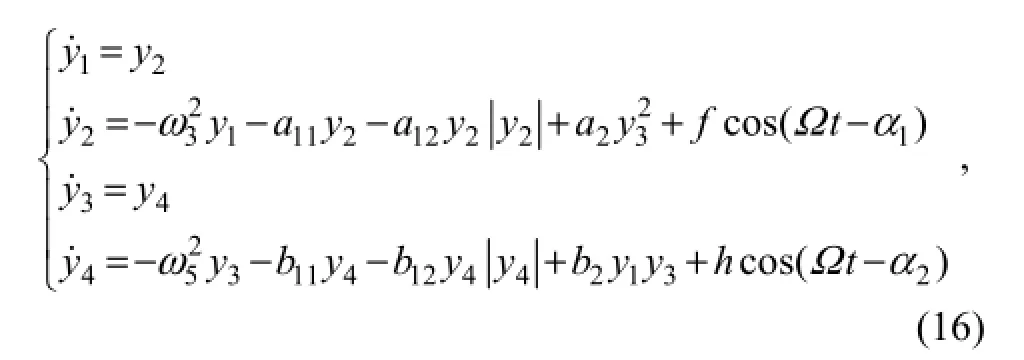
where y1=ξ3, y2=dξ3/dt, y3=ξ5, y4=dξ5/dt, f and h are amplitudes ofF3and M5, respectively. Eq. (16) can be rewritten as following five dimensions autonomy system

where y5=t. The tangent space flow of Eq. (17) is

where Y={y1, y2,…, y5}, U={U1, U2,…, U5}, J is the Jacobian matrix of Eq. (17) with following form

The Lyapunov exponents can be obtained by following formula

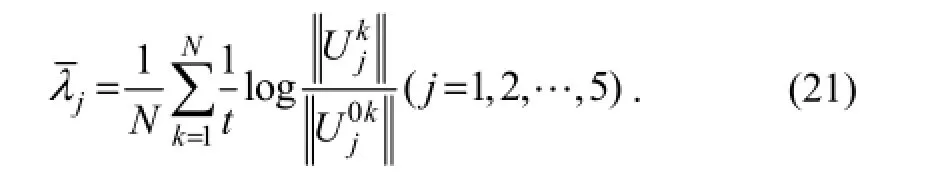
In Eq. (21), the Lyapunov exponents are arranged from large to small. So,λ1is the maximum Lyapunov exponent. The tangent vector U is orthonormalized by Gram-Schmidt method (Zeni and Gallas, 1995) after each iterative cycle, it is selected as the initial tangent vector for the next iterative cycle. Step by step, the Jacobian matrix J brings the tangent vector U approaching to the orientation of the maximum Lyapunov exponent. Using the 4-order Runge-Kutta method in the numerical integration, the maximum Lyapunov exponents are calculated in Section 5.

The main steps of computing the three-dimensional maximum Lyapunov exponent graph are as follows,

1) Select one set of initial values, integrate Eq. (17) for 1000 cycles of wave periods and set the results of the last step as the initial values to calculate the Lyapunov exponents.

2) Calculate the Lyapunov exponents and average them along the phase trajectories using Eq. (18) to Eq. (21), for 100 cycles of wave periods.

3) Repeat steps (1) and (2) for different wave height and wave frequency.

To reveal the nonlinear motions of the platform, the bifurcation graphs, Poincaré maps and power spectrums are also calculated.

5 Results and Analysis

The restoring moment of pitch motion of the spar platform depends on the displaced volume and metacentric height, and both of these parameters change in the time domain due to the heave motion of the platform, as shown in Eq. (5) and Eq. (6). The semotion equations are named Mathieu equations. Haslum and Faltinsen (2000) showed that for a system with no damping, no excitation, and no coupling between pitch and surge, it is possible for the Mathieu instability to occur when the ratios between the natural frequencies of heave mode and pitch mode are close to 0.5, 1, 1.5 and 2.

The platform particulars of Horn Mountain spar platform are shown in Table 1.

Table1 Platform particulars

The ratio between the natural frequencies of heave mode and pitch mode is close to 2:1. Petter (2000), using model experiment, tested the motion of this truss spar platform both in calm water and in waves. To carry out the numerical calculation, the platform parameters of Horn Mountain platform were used and the natural periods and damping were from the results of Petter’s (2000) model experiment. The three-dimensional Maximum Lyapunov exponent graph and bifurcation graph for different wave heights and wave frequencies are shown in Figs.1 and 2.

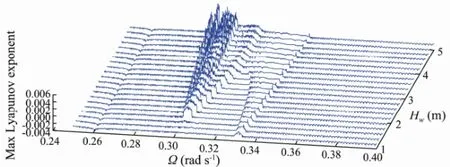
Fig.1 3D Maximum Lyapunov exponents (Hw∈[1, 5] m, Ω∈[0.25, 0.4] rad s-1).

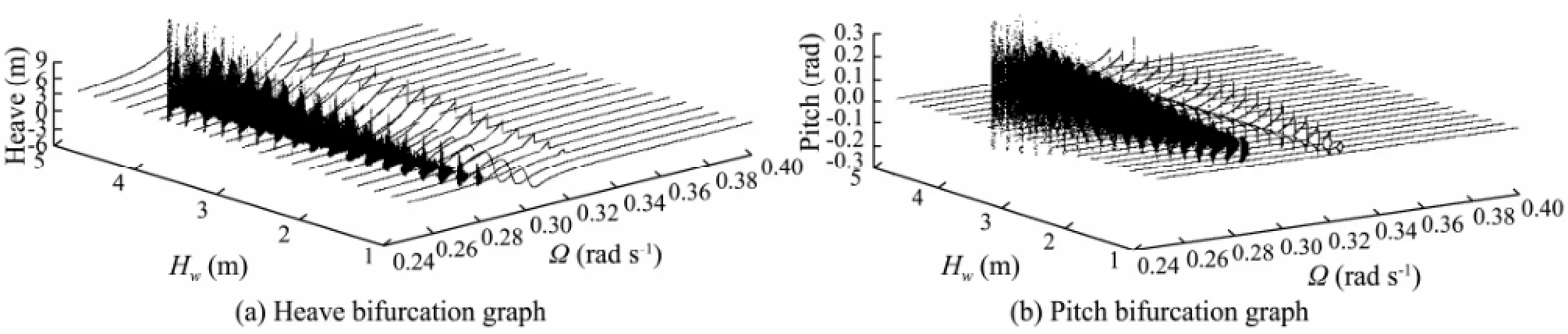
Fig.2 3D bifurcation graphs (Hw∈[1, 5] m, Ω∈[0.25, 0.4] rad s-1).

From these two figures, it is observed that when the wave frequency is close to the natural frequency of the heave mode, the platform moves with nonlinear chaotic and quasi-periodic motions. With increasing wave height, the response amplitudes of heave and pitch increase, and the range of wave frequency which leads to chaotic motion of the platform also increase. Figs.1 and 2 reveal the general nonlinear motions of the platform under different wave conditions.

The maximum Lyapunov exponents and bifurcationgraphs for 3 m and 4m wave heights are shown in Figs.3 and 4. With reference to these two figures, Tables 2 and 3 contain summaries of the dynamic behaviors of heave and pitch of the platform for the 3 m and 4 m wave heights.

Fig.3 Maximum Lyapunov exponents and bifurcation graphs (Hw=3 m). (a) Maximum Lyapunov exponents. (b) Heave bifurcation graph. (c) Pitch bifurcation graph.

Fig.4 Same as Fig.3, but for Hw=4 m.

Table 2 Platform motion analysis (Hw=3 m, Ω∈[0.25, 0.35] rad s-1)

Table 3 Platform motion analysis (Hw=3 m, Ω∈[0.25, 0.35] rad s-1)

Tables 2 and 3 show that the platform undergoes harmonic motion, quasi-periodic motion, chaotic motion and 1/2 sub-harmonic motion for the different wave frequencies. When the wave frequency approaches the natural frequency of the heave mode, the platform moves with quasi-periodic motion and chaotic motion alternately. For a certain range of wave frequencies, the platform moves with totally chaotic motions.

Comparing with case of 4 m wave height, the motions of the platform are more complicated than the case of 3m wave height. As shown in Table 2, with increasing wave frequency, the platform undergoes harmonic motion, alternate quasi-periodic and chaotic motion, chaotic motion, alternate quasi-periodic and chaotic motion, 1/2 sub- harmonic motion, harmonic motion, 1/2 sub-harmonic motion and harmonic motion. The range of wave frequency which leads to chaotic motion of the platform is larger, as shown in Table 3.

To further analyze the nonlinear motions of the platform, the Poincaré maps, power spectrums and time histories under different wave frequencies are calculated, as shown in Figs.5–8.

Fig.5 Time histories and Poincaré maps (Ω=0.28 rad s-1, H=4 m).

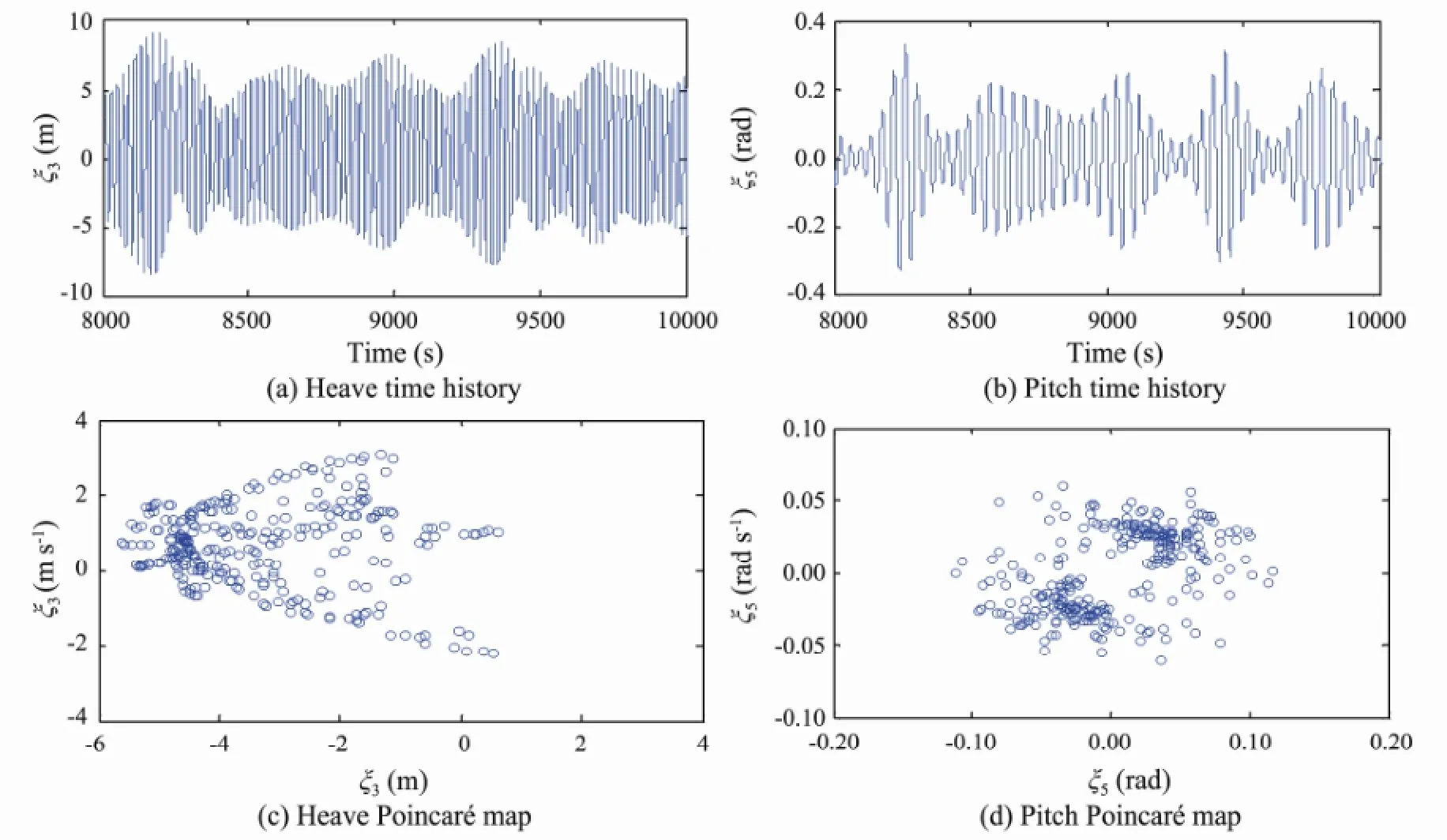
Fig.6 Time histories and Poincaré maps (Ω=0.30 rad s-1, H=4 m).

Fig.7 Time histories and Poincaré maps (Ω=0.31 rad s-1, H=4 m).

Fig.8 Poincaré maps and power spectrums (Ω=0.33 rad s-1, H=4 m).

In Fig.8, Sheaveand Spitchdenote the response power spectrums of heave and pitch of the platform, respectively. Figs.5–8 reveal four different types of motions of the platform, which are harmonic motion, chaotic motion, quasi-periodic motion and 1/2 sub-harmonic motion. As shown in Fig.5, for Ω=0.28 rad s-1, there is only one point on the Poincaré maps of heave and pitch and the platform undergoes harmonic motion. As shown in Fig.6, for Ω= 0.30 rad s-1there is a series of points distribute irregularly in the Poincaré maps of heave and pitch, and the platform moves with the chaotic motions in the heave and pitch modes. As shown in Fig.7, for Ω=0.31 rad s-1the points on the Poincaré maps of heave and pitchare linked together as closed trajectories and the platform moves with quasi-periodic motions. As shown in Fig.8, for Ω=0.33 rad s-1there is 1/2 sub-harmonic frequency component in the response power spectrums of heave and pitch of the platform. The response frequencies of heave are dominated by wave frequency and the response frequencies of pitch are dominated by 1/2 sub-harmonic frequency.

6 Conclusions

The nonlinear dynamic behaviors of the truss spar platform were studied by the numerical simulation method. The coupled heave and pitch motion equations ofthe platform hull were established in regular waves. The maximum Lyapunov exponents, Poincaré map and bifurcation graph were used to analyze the nonlinear motions of the platform. The main conclusions are:

1) The platform undergoes complicated nonlinear motions with changing wave frequency, including quasiperiodic motion, chaotic motion and 1/2 sub-harmonic motion. The three-dimensional maximum Lyapunov exponent graph and bifurcation graph reveal the nonlinear motions of the platform under different wave conditions.

2) When the wave frequency approaches the natural frequency of the heave mode, the platform moves with quasi-periodic motions and the chaotic motions alternately. For a certain range of wave frequencies, the platform moves with totally chaotic motions. The range of wave frequency which leads to chaotic motions of the platform increases with increasing wave height.

3) The platform moves with 1/2 sub-harmonic motion under some wave frequencies, the response frequencies of heave of the platform are dominated by wave frequency, and the response frequencies of pitch of the platform are dominated by 1/2 sub-harmonic frequency component.

In this study, the damping effect was not included. In fact, damping plays a very important role in the coupled nonlinear analysis of a spar platform so that the nonlinear motions can be suppressed efficiently through increasing heave or pitch damping. Depending on the amount of available damping, some nonlinear responses may not occur.

Acknowledgements

The project was supported by the National Natural Science Foundation of China under Grant No. 51179125 and the Innovation Foundation of Tianjin University under Approving No. 1301.

Andrea, R. Z., and Gallas Jason, A. C., 1995. Lyapunov exponents for a duffing oscillator. Physica D, 89: 71-82.

Gavassoni, E., Gonçalves, P. B., and Roehl, D. M., 2014. Nonlinear vibration modes and instability of a conceptual model of a spar platform. Nonlinear Dynamics, 74 (1): 809-826.

Haslum, H. A., and Faltinsen, O. M., 2000. Alternative shape of spar platforms for use in hostile areas. In: Proceedings of the 31st Offshore Technology Conference. Huston, USA, 217-288.

Jameel, M., Ahmad, S., Islam, A. B. M. S., and Jumaat, M. Z., 2013. Non-linear dynamic analysis of coupled spar platform. Journal of Civil Engineering and Management, 19 (4): 476-491.

Lim, S. J., Rho, J. B., and Choi, H. S., 2005. An experimental study on motion characteristics of cell spar platform. In: Proceedings of the International Offshore and Polar Engineering Conference. Seoul, Korea, 233-237.

Petter, A. B., 2000. Dynamic response analysis of a truss spar in waves. PhD thesis. University of Newcastle, Newcastle.

Rho, J. B., and Choi, H. S., 2004. Vertical motion characteristics of truss spars in waves. In: Proceedings of the International Offshore and Polar Engineering Conference. Toulon, France, 662-665.

Sadeghi, K., Incecik, A., and Downie, M. J., 2004. Response analysis of a truss spar in the frequency domain. Journal of Marine science and technology, 8: 126-137.

Shen, W. J., and Tang, Y. G., 2011. Stochastic analysis of nonlinear coupled heave-pitch motion for the truss spar platform. Journal of Marine Scienceand Application, 10: 471-477.

Tahar, A., and Kim, M. H., 2008. Coupled-dynamic analysis of floating structures with polyester mooring lines. Ocean Engineering, 35: 1676-1685.

Tang, Y. G., 2008. Ocean Engineering Structural Dynamics. Tianjin University Press, Tianjin, 291pp (in Chinese).

Weggel, D. C., and Roesset, J. M., 1994. Vertical hydrodynamic forces on truncated cylinders. In: Proceedings of the 4th International Offshore and Polar Engineering Conference. Osaka, Japan, 210-217.

Wolf, A., Swift, J. B., Swinney, H. L., and Vasrano, J. A., 1985. Determining Lyapunov exponents from a time series. Physica D, 16: 285-317.

Xu, L. X., and Jing, X. N., 2013. Calculating riser dynamic effects on spar motions in waves. In: Proceedings of the 23rd International Offshore and Polar Engineering Conference. Anchorage, Alaska, USA, 78-84.

Yan, H. M., 2010. Computations of fully nonlinear three- dimensional wave-body interactions. PhD thesis. Massachusetts Institute of Technology.

Yang, M., Teng, B., Ning, D., and Shi, Z., 2012. Coupled dynamic analysis for wave interaction with a truss spar and its mooring line/riser system in time domain. Ocean Engineering, 39: 72-87.

Zeni, A. R., and Gallas, J. A. C., 1995. Lyapunov exponents for a duffing oscillator. Physica D, 89: 71-82.

Zhao, J. R., Tang, Y. G., and Shen, W. J., 2010. A study on the combination resonance response of a classic spar platform. Journal of Vibration and Control, 16 (14): 2083-2107.

Zhao, J. R., 2010. Study on nonlinear coupling dynamic response of a classic spar platform. PhD thesis. Tianjin University, Tianjin (in Chinese).

(Edited by Xie Jun)

(Received February 11, 2014; revised April 21, 2014; accepted January 12, 2015)

J. Ocean Univ. China (Oceanic and Coastal Sea Research)

DOI 10.1007/s11802-015-2592-2

ISSN 1672-5182, 2015 14 (5): 795-802

http://www.ouc.edu.cn/xbywb/

E-mail:xbywb@ouc.edu.cn

* Corresponding author. E-mail: liuliqin@tju.edu.cn