HEC-HMS水文模型在数据稀缺山区流域中的应用——以乌鲁木齐河流域为例
穆艾塔尔·赛地, 阿不都·沙拉木, 丁建丽, 崔春亮
(1.新疆大学 资源与环境科学学院, 新疆 乌鲁木齐830046;
2.绿洲生态教育部重点实验室, 新疆 乌鲁木齐830046; 3.新疆水利水电科学研究院, 新疆 乌鲁木齐 830049)
HEC-HMS水文模型在数据稀缺山区流域中的应用——以乌鲁木齐河流域为例
穆艾塔尔·赛地1,2,3, 阿不都·沙拉木3, 丁建丽1,2, 崔春亮3
(1.新疆大学 资源与环境科学学院, 新疆 乌鲁木齐830046;
2.绿洲生态教育部重点实验室, 新疆 乌鲁木齐830046; 3.新疆水利水电科学研究院, 新疆 乌鲁木齐 830049)
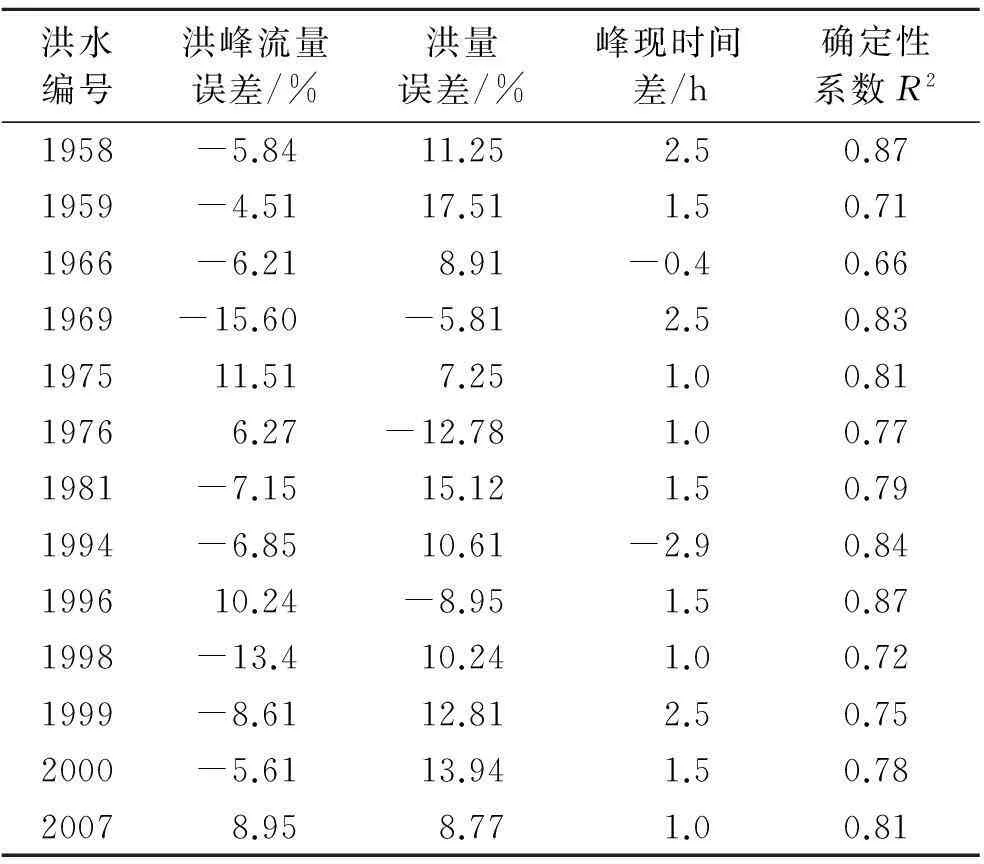
摘要:[目的] 评价HEC-HMS分布式水文模型在干旱区资料稀缺内陆河流域洪水模拟预报中的适用性。 [方法] 以乌鲁木齐流域上游为例,结合流域实测水文气象资料,率定模型参数、建立并验证HEC-HMS模型。[结果] 1957—2009年乌鲁木齐河上游流域13场历史洪水模拟中,HEC-HMS模型洪水模拟确定系数R2取值分布在0.67~0.87之间,洪峰流量模拟相对误差均小于15.6%,模拟精度较高。[结论] 建立的HEC-HMS模型有效,模型参数的率定合理以及HEC-HMS模型在干旱数据稀缺山区流域洪水模拟中具有较好的适用性。
关键词:HEC-HMS模型; 山区流域; 洪水模拟; 乌鲁木齐河
水文现象随空间和时间而变化,具有空间和时间尺度。对于空间尺度影响而言,流域面积大小是其主要影响因素,不同大小的流域因尺度不同,水文特性也具有显著的差异;不同时间尺度的水文特征值也会呈现出不同的变化特征[1-6]。HEC-HMS〔hydrologic engineering center(HEC)hydrologic modeling system(HMS)〕模型是美国陆军工程兵团水文工程中心(HEC)开发的一种具有物理概念的半分布式次降雨径流模型,主要用于树状流域径流过程的模拟[7]。其首先根据流域DEM,将流域划分成若干单元或自然子流域,通过坡面汇流和河道汇流,最后演算至流域出山口断面。该模型除了能够模拟流域控制断面的流量过程外,还可计算任一单元出口的径流过程,在国内外广泛应用于无实测资料地区中、小河流的山洪预警预报[8-10]。但是,目前在我国西北干旱区内陆河流域应用该模型模拟洪水过程的研究较少[6-11]。本研究以西北干旱区典型内陆河流域——乌鲁木齐河为例,以1957—2009年乌鲁木齐河上游13场较大的混合型历史洪水以及同期的流量和雨量监测数据为基础,进行模拟和预报,评价该模型在干旱区资料稀缺内陆河流域洪水模拟预报中的适用性。
1HEC-HMS模型
1.1 HEC-HMS对径流形成过程的概化
HMS模型将子流域分为地面和水体(河流和湖泊)两部分,降在地面上的雨水经过植物截留、地面填洼后形成坡面流,降在水体的雨水直接形成径流。HMS将近地表土壤水的水平运动与坡面流合并为直接径流,而仅仅将地下水含水层中水分的运移视作基流[11]。
1.2 HMS中的计算模块
在HEC-HMS模型主要包括4个模块(图1),分别为净雨计算模块、直接径流(坡面流和壤中流)计算模块、基流计算模块和河道洪水演算模块。在每一模块内,根据资料情况以及计算日的要求等,可以采用不同的计算方法[11]。
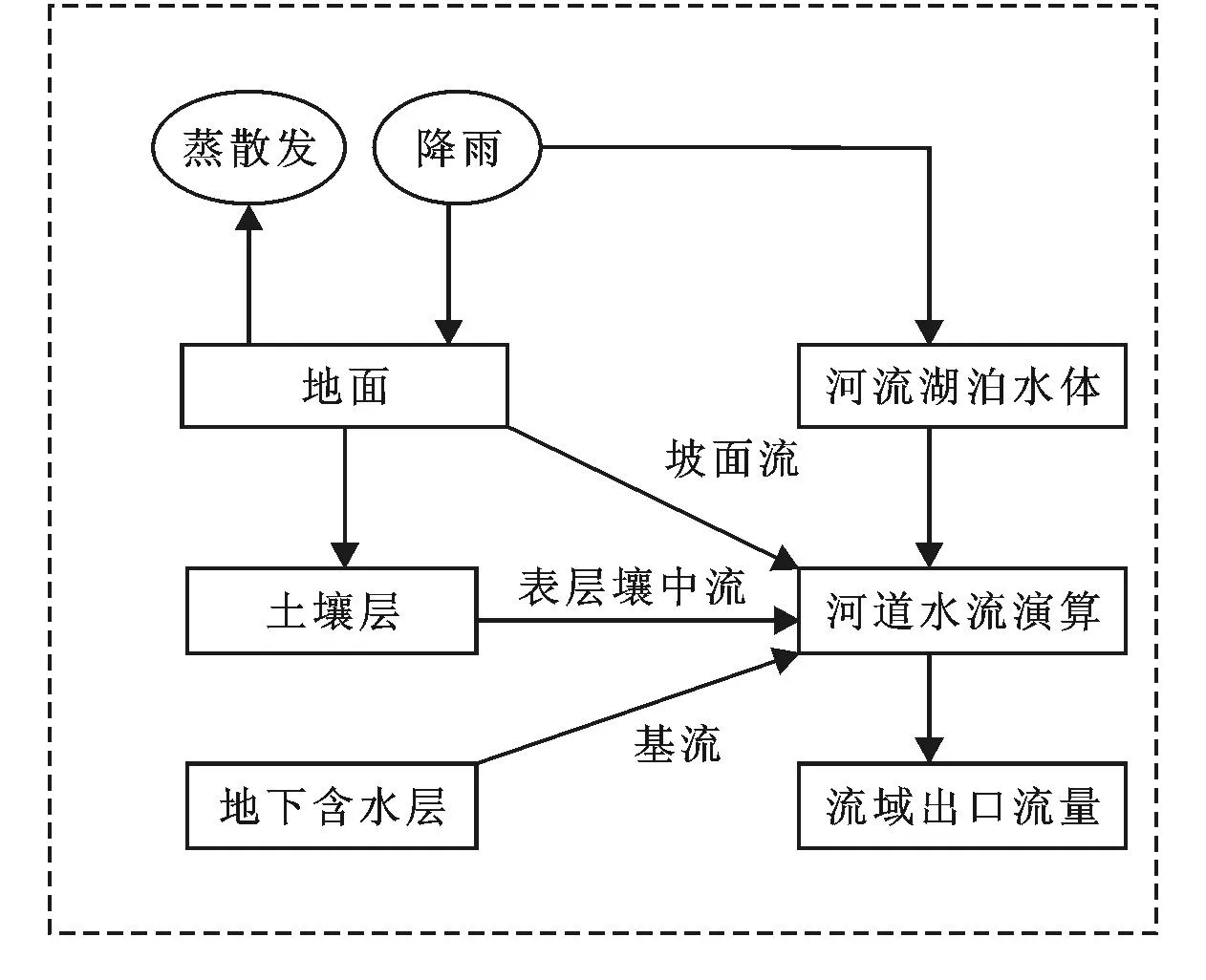
图1 HEC-HMS对流域径流概化图
1.3 产流计算
1.3.1初损后损法方法假定一个常数fc,作为一场降雨过程中的最大潜在降雨损失,Pt代表在时段t到(t+Δt)内的平均雨深;Ia为初始损失;代表径流形成之前的截留和填洼蓄水量;Pi为累计降雨;净雨Pet的计算方法为[11]:
当∑pi 当∑pi>Ia,pt>fc时,pet=pt-fc (1) 当∑pi>Ia,pt 1.3.2SCS-CN模型该模型认为净雨量为累计降雨、土壤覆盖、土地利用以及前期土壤含水量的函数,即: (2) 式中:Pe——t时刻对应的累计净雨(mm);P——t时刻对应的累计降雨深(mm);Ia——初始缺水量(mm);S——最人持水量(mm)。 模型认为在累计降雨超过初始缺水前不产流。SCS建立的Ia与S的经验关系为: Ia=0.2S (3) 累计净雨计算公式为: (4) 任一时段的净雨量等于时段末与时段初累计净雨的差值,通过中间参数CN(径流曲线号码),可以建立最大持水量与流域特征的关系为: (5) 1.3.3Green和Ampt损失模型Green和Ampt损失模型是概念性下渗模型,某时段的降雨损失可计算为: (6) 式中:f——降雨损失(cm);K——饱和导水率(cm/s);θs——饱和含水率(cm3/cm3);θi——初始含水率(cm3/ cm3);S——湿润锋面处土壤水吸力(cm);F——累计降雨损失(cm)。某时段的净雨量可通过平均降雨深减去公式(6)计算的降雨损失值来表示。 1.3.4SMA模型SMA模型是一个连续模拟模型,能够模拟水分在植被、土地表面、土壤层内以及地下水含水层中的蓄水和运移情况。已知降雨和潜在蒸散发(ET),模型可以计算流域地面径流、地下径流、蒸散发损失以及向深层的渗透损失[12-14]。 HEC-HMS模型计算径流过程主要通过经验模型,即传统的单位线模型,包括User-Specified单位线、参数单位线和综合单位线;同时概念性模型,即运动波模型,也广泛应用[15]。相关模型在划分子流域的基础上,利用River Tools建立各子流域的面积—距离函数,根据该函数产生单位线。其中,距离的计算公式为: (7) 式中:V——流速(m/s);t——汇流时间(s);a——经验参数;S——子流域坡度。 HEC-HMS模型提供的基流计算方法有常数月变化模型、指数消退模型及线性水库模型。其中指数消退模型认为任一时刻的基流流量Qt与初始基流流量Q0的关系为: Qt=Q0Kt (8) 式中:Qt——t时刻的基流流量(m3/s);Q0——初始基流流量(m3/s);K——指数衰减常数。 HEC-HMS模型包含了许多可供选择的河道洪水演算模型,包括滞后模型,Muskingum模型,改进的Puls模型,Muskingum Cunge模型等。考虑河网汇流的特点,在HMS模型中设置了河道合流模型[16]。 2乌鲁木齐河流域概况 乌鲁木齐河位于天山山脉北坡中段,发源于天山天格尔Ⅱ峰附近1号冰川,源头海拔4 479 m以上,自南流向北东北,出山口后,至乌拉泊折向正北,横穿乌鲁木齐市区,流向西北,最后流入准噶尔盆地南缘米泉市西北部的古尔班通古特沙漠消失,全长214 km,是一条冰雪融水、降雨及地下水混合补给的河流。根据1958—2009年流域出山口的英雄桥水文站资料统计,其多年平均径流量为2.44×108m3,年最大径流量为3.44×108m3,夏季径流量占年径流量的比重最大,达69.2%,春、秋和冬季径流量均较小,占年径流量的比重分别为10.3%,15.7%和4.8%。径流组成大致为冰川融水占12%,融雪水占37%,降雨占36%,地下水占15%[18]。乌鲁木齐河流域上游多年平均降水量为457 mm,上游洪水按成因可分为冰雪融水型、暴雨型和混合型;洪水主要来自上游山区,当春季气温骤升,前山积雪消融而形成春汛,夏秋季一般在小河沟山前冲积扇地带发生局部地区暴雨。据历史记载乌鲁木齐河上游地区最大暴雨降水量达20 mm,每分钟降水量强度在20 mm以上,每1 km2降雨平均产流量大于2~4 m3/s,可以产生较大的洪水,具有很强的破坏力;另一种是混合型洪水,每当3 000~5 000 m高空气温上升到零度以上,并持续3~5 d,加上较强的暴雨径流,即可发生大洪水,常造成严重灾害[19]。 3洪水模拟结果与分析 采用流域DEM数据,经过ArcView的HEC-GeoHMS模块数据处理,得到乌鲁木齐河上游的河网分布;按照子流域面积大于2 km2,小于20 km2的原则,将整个乌鲁木齐河上游地区划分46个自然子流域,通过子流域和河网分布的空间叠加获得乌鲁木齐河上游HEC-HMS模型结构,结果如图2所示。 图2 研究流域DEM及HEC-HMS模型流域结构 基于由DEM生成的HEC-HMS模型结构数据和乌鲁木齐河上游的降雨资料,利用克里格空间内插方法推算子流域降雨量。推算子流域降雨量数据后,采用初损后损法和单位线法分析子流域的单位线、再利用指数消退基流模型和Muskingum河道洪水演算模型进行洪水计算[8,11]。 利用可视化数据存储系统HEC-DSSVue模块建立乌鲁木齐河上游的降雨数据库和流量数据库,将乌鲁木齐河上游大西沟气象站、跃进桥水文站和英雄桥水文站在1957—2009年的13场混合型洪水雨量时间序列与同期的流量数据输入该数据库,通过HEC-DSSVue的数学函数功能,将不规则时间序列数据进行时间插值,转成规则时间序列数据,最终得到每场降雨雨量数据序列和每场洪水观测流量数据序列。 根据气象和水文站的分布情况,利用泰森多边形确定各控制站覆盖的子流域,同一控制站内的子流域采用相同的雨量资料。乌鲁木齐河上游流域境内没有影响洪水汇流过程的大型水库、泉水以及起分流作用的复杂水利工程等,因此将其概化为子流域、河段及结点等元素,各元素之间的拓扑关系构成流域产汇流系统。建立流域模型产汇流系统后,利用HEC-HMS模型计算乌鲁木齐河上游产流〔公式(1)—(6)〕、直接径流公式(7)、基流模拟公式(8)和河道汇流等,在此基础上,对乌鲁木齐河上游13场洪水进行模拟和验证,模拟及误差分析结果详见表1。 表1 HEC-HMS模型洪水模拟结果 由表1可以看出,利用HEC-HMS模型模拟乌鲁木齐河上游洪峰流量的相对误差均不超过15.6%,确定性系数最高达0.87;在13场混合洪水模拟中,模拟与实测洪峰流量值的相对误差小于10%的有9场,确定性系数大于0.70的有12场,表明HEC-HMS模型的模拟结果较好,可用于乌鲁木齐河上游山区流域的水文模拟。 在模型验证的基础上进一步对乌鲁木齐河上游2015—2020年洪水发生概率进行初步预测,结果如表2所示。表2说明,2015—2020年乌鲁木齐河上游除了2015和2018年预测平均流量小于多年平均流量外,其他年份预测平均流量均大于多年平均流量,可能发生的洪水风险较大,应适当重视。在此初步预测基础上,为了提高预测精度需要进行深入的专题研究。 表2 HEC-HMS模型2015-2020年洪水模拟结果 注:模拟相对误差=(预测平均流量-多年平均流量)/多年平均流量×100。 4结 论 HEC-HMS模拟系统具有很好的操作界而和强大的可视化功能,广泛应用于缺乏长序列实测资料地区洪水模拟预报,经众多国内外研究验证效果较好。本研究采用HEC-HMS模型与ArcView地理信息系统软件结合,利用实测水文和气象资料,在率定模型参数的基础,建立HEC-HMS模型,验证模拟结果,评价该模型在干旱区山区流域洪水模拟中的适用性。结果表明,HEC-HMS模型在乌鲁木齐河上游流域13场混合型历史洪水模拟中效果比较理想,确定系数R2分布在0.67~0.87之间,洪峰流量的模拟误差均小于15.6%。可知,HEC-HMS模型在资料稀缺干旱区内陆河小流域洪水模拟预报中具有较好的适用性。 [参考文献] [1]林峰,陈桂芳. HEC-HMS分布式水文模型的时间尺度效应研究[J].吉林师范大学学报:自然科学版,2009(3):132-135. [2]Argiriou A A, Bellas-Velidis I, Kummert M, et al. A neural network controller for hydronic heating systems of solar buildings [J]. Neural Networks, 2004,17(3):427-440. [3]Takeuchi K, Ao T, Ishidaira H. Introduction of block-wise use of TOPMODEL and Muskingum-Cunge method for the hydroenvironmental simulation of a large ungauged basin [J]. Hydrological Sciences Journal, 1999,44(4):633-646. [4]彭盛华,赵俊琳,袁弘任. GIS技术在水资源和水环境领域中的应用[J].水科学进展,2001,12(2):264-269. [5]Zhou M C, Ishidaira H, Hapuarachchi H P, et al. Estimating potential evapotranspiration using Shuttle worth-Wallace model and NOAA-AVHRR NDVI data to feed a distributed hydrological model over the Mekong River basin [J]. Journal of Hydrology, 2006,327(1):151-173. [6]丁杰,李致家,郭元,等.利用HEC模型分析下垫面变化对洪水的影响:以伊河东湾流域为例[J].湖泊科学,2011,23(3):463-468. [7]梁钟元,贾仰文,李开杰,等.分布式水文模型在洪水预报中的应用研究综述[J].人民黄河,2007,29(2):29-32. [8]林峰,陈莹,陈兴伟,等.基于HEC-HMS模型的时间步长对次洪模拟的影响分析[J].山地学报,2011,29(1):50-54. [9]王中根,刘昌明,左其亭,等.基于DEM的分布式水文模型构建方法[J].地理科学进展,2002,21(5):430-439. [10]吴迪,赵勇,裴源生,等.气候变化对澜沧江—湄公河上中游径流的影响研究[J].自然资源学报,2013,28(9):1569-1582. [11]李燕,孙永寿,朱朝霞. HEC-HMS及其在篓子沟流域的应用研究[J].中国农村水利水电,2009(3):47-49,52. [13]刘昌明,夏军,郭生练,等.黄河流域分布式水文模型初步研究与进展[J].水科学进展,2004,15(4):495-500. [14]鲍新华,洪梅,周祖昊,等.基于DEM的等流时单元法在大流域分布式水文模型中的应用[J].吉林大学学报:地球科学版,2010,40(2):337-341. [15]李燕,陈孝田,朱朝霞. HEC-HMS在洪水预报中的应用研究[J].人民黄河,2008,30(4):23-24. [16]雍斌,张万昌,赵登忠,等. HEC-HMS水文模型系统在汉江褒河流域的应用研究[J].水土保持通报,2006,26(3):86-90. [17]李瑞雪,张明军,金爽,等.乌鲁木齐河流域气候变化的区域差异特征及突变分析[J].干旱区地理,2010,33(2):243-250. [18]穆艾塔尔·赛地,阿不都·沙拉木,崔春亮,等. 新疆天山北坡山区流域水文特征分析[J].水文,2013,33(2):87-92. [19]姚海燕,张民.乌鲁木齐河流域水管理信息系统[J].水文,2006,26(2):78-80,96. Application of HEC-HMS in Data-Insufficient Mountainous Watersheds -A Case Study from Urumqi River Basin Muaitaer·Saidi1,2,3, Abudou·Shalamu3, DING Jianli1,2, CUI Chunliang3 (1.CollegeofResourceandEnvironmentSciences,XinjiangUniversity,Urumqi,Xinjiang830046,China; 2.KeyLaboratoryofOasisEcologyofMinistryofEducation,Urumqi,Xinjiang830046,China; 3.XinjiangWaterResourcesResearchInstitute,Urumqi,Xinjiang830049,China) Abstract:[Objective] To evaluate the suitability of HEC-HMS model in flood warning forecast in data-insufficient mountain watersheds. [Methods] This paper established and validated HEC-HMS model for flood simulation in the mountainous watersheds of Urumqi River basin with limited hydro meteorological data. [Results] The established HEC-HMS model simulated thirteen typical historical flood streams in the watershed with relatively good performances of Urumqi River basin in 1957—2009. The determination coefficients of the simulation varied between 0.67~0.87 and the simulation error for each flood stream was less than 15.6%。[Conclusion] The calibration of HEC-HMS model parameters is reasonable and the model is of practical application in the data-scarce arid mountainous watersheds for flood stream simulation. Keywords:HEC-HMS model; mountainous watersheds; flood simulation; Urumqi River 文献标识码:B 文章编号:1000-288X(2015)06-0140-04 中图分类号:TV121+.4 收稿日期:2014-10-23修回日期:2014-11-29 资助项目:新疆维吾尔自治区科技计划项目“基于RiverWare模型的抗旱减灾水资源管理决策支持系统研究”(20126013); 国家自然科学基金项目(51069017); 新疆维吾尔自治区公益性科研院所基本科研业务项目(KY2014044); 新疆大学绿洲生态重点实验室开放基金项目(XJDX0201-2013-04) 第一作者:穆艾塔尔·赛地(1984—),女(维吾尔族),新疆自治区策勒县人,博士研究生,工程师,主要从事水文水资源方面的研究。E-mail:895798730@qq.com。1.4 直接径流过程的模拟
1.5 基流计算模型
1.6 河道洪水演算模型
3.1 子流域划分
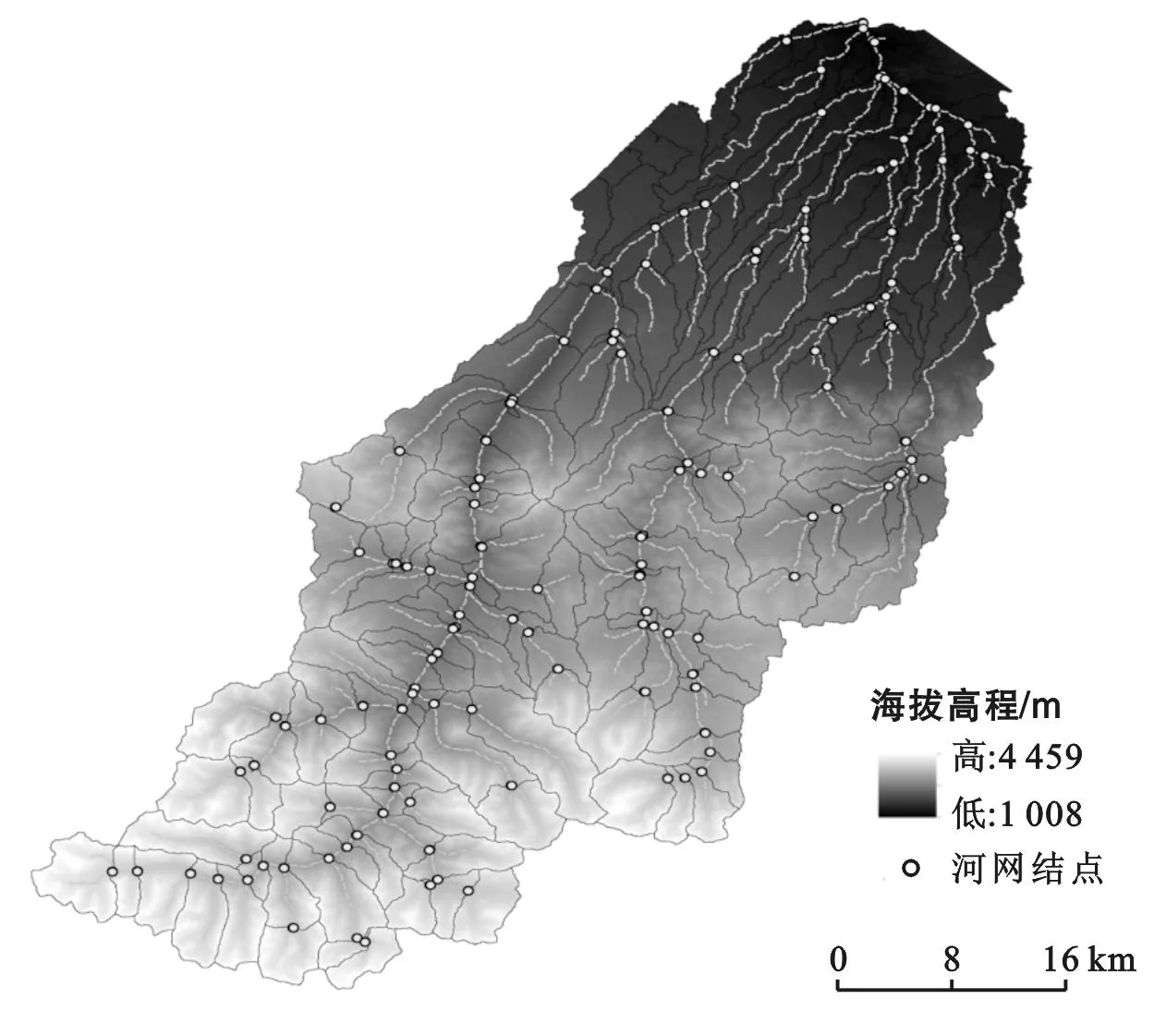
3.2 计算模型
3.3 参数率定与径流模拟