遗传算法和模糊神经网络在齿轮传动中的应用

张健，王笑竹（营口理工学院，辽宁 营口 115014）

遗传算法和模糊神经网络在齿轮传动中的应用

张健，王笑竹（营口理工学院，辽宁 营口 115014）

基于遗传算法优化模糊神经网络齿轮传动机构优化的新模型，首先将各参数用二进制串表示，用适合度函数衡量算法的收敛状况。然后寻找最优模糊隶属函数参数，按适值选取最后一代群体中N个可能具有全局性的进化解，分别以该进化解为初始权值，用BP神经网络进行求解，比较N个由神经网络求得最优解，从而获得全局最优解。Matlab仿真结果表明所构造的识别模型预测误差非常小。

电梯群控；遗传算法（GA）；BP神经网络；模糊神经网络

针对模糊神经网络齿轮传动控制中存在的缺陷，提出遗传算法(GA)优化模糊神经网络齿轮传动的新模型。GA训练模糊BP神经网络能够克服网络建模中产生的局部极小的缺点[1]，通过对齿轮传动进行优化，确保大概率地获得全局最优解。

1 GA优化模糊神经网络的模型

1.1确定目标函数

在齿轮传动控制中，选用斜齿圆柱齿轮减速器，有关参数如下：滚筒圆周力F=900N，带速V=2.3m/s，小齿轮材料40MnB调质处理，大齿轮材料ZG35SiMn调质处理，为了节省空间，选用齿轮中心距最小建立目标函数。如图1所示，以d1，d2分别表示小齿轮、大齿轮的分度圆直径， 齿轮中心距表达式为：

齿数比带人公式（1），得

1.2选取设计变量及建立模糊约束条件

由目标函数的表达式知，f(x)是小齿轮齿数：z1、法面模数mn、螺旋角β和齿数比u的函数，但u为已知量，因此，宜取mn、z1、β为设计变量，即

图1 齿轮结构图

模糊约束条件分为性能约束和边界约束。由于边界约束是指尺寸或变量大约在某数值附近取值，以及性能约束中的许用值受设计水平、制造水平、材质好坏、使用条件等因素的影响，约束条件具有一定的模糊性[2]。

（1）小齿轮齿数的限制。对于动力传动，要求齿轮齿数17＜Z1＜30；

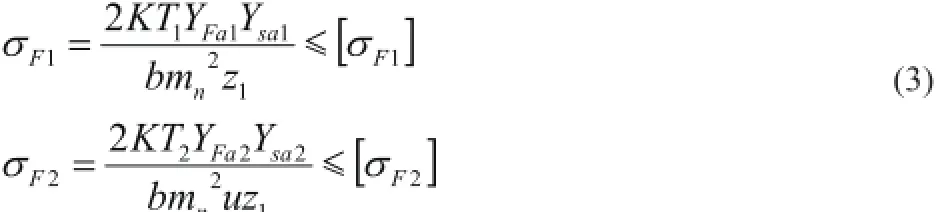
式（3）中，YFa1为小齿轮齿形系数，Ysa1为小齿轮应力集中系数，YFa2为大齿轮齿形系数，Ysa2为大齿轮应力集中系数，[σF]为蜗轮弯曲强度模糊许用应力。

BP神经网络克服对输入样本具有严格分布假设的要求，能适应模糊约束条件的高度非线性和包含大量复杂信息的特点。但BP神经网络的训练具有一定的盲目性。忽略了对影响因素中的定性指标的分析，显然是不合理的、片面的。由于BP神经网络在本质上是梯度下降法，所要最小化的目标函数又比较复杂，因此学习过程收敛速度慢且容易陷入局部极小点[3]。

1.3模糊BP神经网络建模

针对BP神经网络存在的不足，我们首先将模糊系统和神经网络结合起来构建模型。模糊神经网络一般是以神经网络为框架的一种模糊推理系统。我们假设系统有n个输入xi(i=1,2,…n)，输出为y，则对于模糊规则Rj(j=1,2,…l)，系统的输入输出模糊模型为：

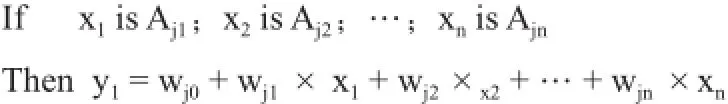
那么模型的全局输出可以表示为：

其中，x 为输入变量；

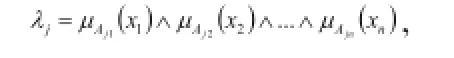
∧表示进行模糊逻辑与运算，即取小运算，μAji(xi)表示xi对模糊子集Aji的隶属度函数值，Aji用高斯型隶属度函数表示：

其中，Cji为隶属度函数的中心值，bi为隶属度函数的宽度。构造5层模糊BP神经网络的网络模型如图2所示。

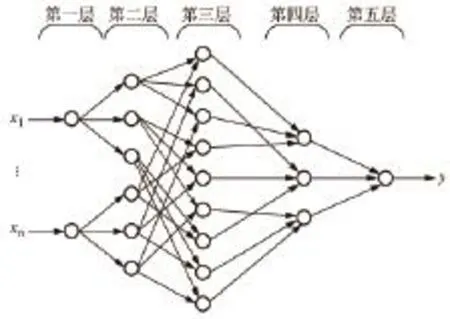
图2 模糊BP神经网络结构

第1层为输入层，每个节点代表一个输入变量， Oi1= Ii1= xi和；上标表示层序，1表示第1层。

第2层为模糊化层，通过一个或多个隶属函数将输入变量模糊化，

式中f(*)为相应的隶属函数。

第3层为模糊条件层，该层节点进行模糊规则条件部分的组合配合，实现各个输入模糊值的“乘”运算。

第4层为模糊判决层，该层节点与第3层节点的连接关系代表了模糊规则的结论，得出对应输出节点模糊值的大小。

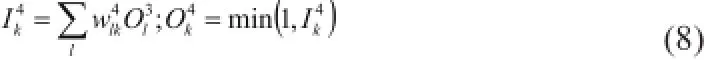
第5层为去模糊化层，该层节点实现“解模糊化”将输出量从模糊值还原成数值形式，实现输出的清晰化。

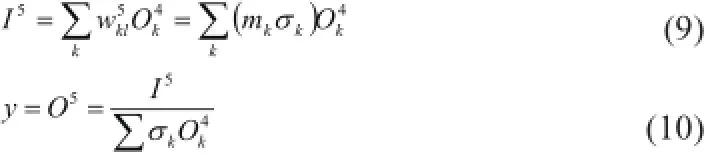
模糊BP神经网络的结构模型在继承神经网络的学习能力的同时，还可以自动总结模糊规则、调整隶属度函数、处理模糊信息和完成模糊推理。另外模糊BP神经网络的节点及参数均有明显的实际应用含义，使得网络模型具备可解释性能。因此，模糊BP神经网络的性能优于单一的模糊或神经网络结构。

1.4用GA优化模糊BP神经网络的训练算法

GA具有全局搜索能力，利用GA优化模糊BP神经网络可以使整个网络达到全局的最优点，能够提高网络评估的准确性。为了用GA学习调整模糊神经逻辑(FNC)网络的隶属变函数参数(cij，bi)值，我们首先将各参数用二进制串表示，假定参数的分量均在预定的范围[θmin，θmax]内变化，那么参数串的表示值和实际参数之间的关系为：

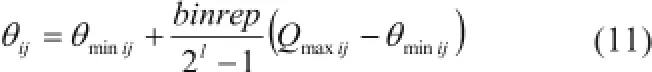
式中，binrep表示由1位字符串所表示的二进制整数。在GA中，交叉率Pc和变异率Pm大小对GA的性能有很大的影响，一般选取范围Pc为0.5-1.0；Pm为0.005-0.1。针对不同的优化问题，需要反复的实验来确定。这里我们采用一种自适应Pc和Pm方法：用适合度函数来衡量算法的收敛状况，其表达式为：

其中，fmax、fp分别为群体中的最大适合度和平均适合度，fmax—fp体现了群体的收敛程度，K1，K2为均小于1.0的常数。

如果从过程操作数据中，我们已经得到样本数据(ei，Δei，yi*)；1≤ I ≤ m，那么对于上述模糊神经网络模型，问题成为：当输入e = ei；Δe = Δei时，则输出yi* = yi；寻找最优模糊隶属函数参数θi=[cij，bj]，使得：

式中，yi表示希望输出值，yi*表示FNC输出值。经过GA算法训练好FNC后，我们采用在线学习方式，利用BP快速梯度算法调节网络的权值，定义：

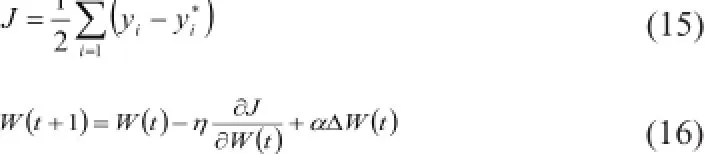
其中，η为学习因子，α为动量因子。

当采用GA学习BP网络权值时，要有效地配合使用交叉和变异算子，在遗传算法中，交叉算子因其全局搜索能力强而作为主算子，变异算子因其搜索能力强而作为辅助算子。一般来讲，交叉概率Pc要取较大的值，而变异概率Pm相对要小的多，这样，群体在即将寻到最优值时，不会因变量变异而破坏此进程。

遗传操作完成之后，按适值选取最后一代群体中N个可能具有全局性的进化解，分别以这些解为初始权值，用BP神经网络进行求解，比较N个由神经网络求的最优解，从而获得全局最优解[4]。

图4 GA训练模糊BP网络的样本输出

从Matlab的仿真结果可以看出，训练结果非常满意，预测误差非常小，说明利用GA优化模糊神经网络对齿轮传动机构优化是可靠的。

3 结语

本文通过将BP神经网络、模糊逻辑算法和遗传算法三者结合起来建立齿轮传动机构优化的新模型，充分发挥三者的优势，取长补短，使构成的模型具有三者的优点。利用Matlab对样本数据进行实证分析，仿真结果表明所建模型评估误差非常小，比利用其中一种或两种方法对于齿轮传动机构优化更具准确性和快速性。

2 仿真与实现

利用Matlab软件通过编程搭建本设计的基于GA优化的模糊神经网络模型[5]，通过输入样本数据分别对网络进行训练和测试。其中，图3为原始样本数据的输出函数曲面，图4是原始样本数据经过本文所设计的GA优化模糊BP神经网络的训练输出函数曲面，可以看出，本文所构造的GA优化模糊BP神经网络训练得样本数据和原始数据的误差非常小。

图3 原始样本输出

[1] 龚安, 王霞, 姜焕军. 基于遗传算法的BP神经网络在油田措施规划预测中的应用[J]. 计算机系统应用, 2006(11): 21 - 24．

[2] 席平原, 李贵三, 胡恒银, 申屠留芳. 应用遗传算法和神经网络的工程电梯传动机构模糊优化设计[J]. 工程设计学报, 2005(10): 273 - 275．

[3] 张卫东, 韩云昊, 米阳. 基于GA-BP模糊神经网络的商业银行信用风险评估[J]. 工业工程与管理, 2006(5): 81 - 84．

[4] Arslan A. Determination of fuzzy logic membership function using genetic algorithms [J]. Fuzzy Sets and Systems,2001(5): 297 - 306.

[5] 唐桂忠, 张广明. GA模糊神经网络在电梯群控交通流识别中应用[J]. 微处理机, 2005(5): 46 - 48.

The Gear Drive Mechanism Applying Genetic Algorithm and Fuzzy Neural Networks

The paper proposes a new model of gear transmission mechanism based on genetic algorithm to optimize the fuzzy neural network. The various parameters are expressed by binary string, and the convergence is evaluated using fitness function. The optimal fuzzy membership function parameters can be therefore found. According to fitness N-solutions are selected based on the overall evolution of the last generation in population. Then the evolutionary solution ia regarded as the initial weights, the final solution can be found by using BP neural network. By comparing these solutions from neural network, the global optimal solution is obtained. Matlab simulation results show that the constructed model has a very small prediction error.

Elevator group control system; Genetic algorithm; BP neural network; Fuzzy neural network

B

1003-0492(2015)03-0092-03

TP273

张健（1981-），男，实验师，在读博士研究生，现就职于营口理工学院机电工程系，主要从事电力电子与电力传动，自动控制、电机控制等方向的研究。

王笑竹（1982-），女，讲师，硕士研究生，现就职于营口理工学院机电工程系，主要从事超声电机与压电材料方向的研究。