基于遗传算法的弹药集装模块垛位优化*

任俊鹏 严 平 谭 波

(海军工程大学兵器工程系 武汉 430033)



基于遗传算法的弹药集装模块垛位优化*

任俊鹏 严 平 谭 波

(海军工程大学兵器工程系 武汉 430033)

垛位优化是弹药库房管理中的重要内容。论文首先对库房中的弹药集装模块的总搬运距离和各个垛堆的作业频率建立多目标优化模型——弹药集装模块垛位优化模型;然后采用权重系数变换法的遗传算法对多目标问题进行优化计算,并结合实例给出了求解的具体步骤和操作过程。最后通过Matlab对实例尺寸为15m×10m×5m的库房垛位优化进行计算,垛位优化初始解经过计算由最初的139.5697将降为132.5724。通过计算可知优化解的降幅达到了5.01%,证明了这一方法的有效性。

垛位优化; 集装模块; 遗传算法

Class Number TJ410.3

1 引言

海军弹药保障正逐步摆脱“人推肩扛”的传统保障模式,实现以托盘集装箱为基础的模块化储存和机械化搬运。托盘化的弹药在进入弹药库房后,如何确定其在库房中堆垛位置就成为一个关键的问题。垛位分配是否合理对今后弹药的作业效率将产生直接的影响。如果弹药集装模块的垛位分配合理,则有利于库房中进行机械搬运作业,以提高弹药保障效率;反之,就会出现不同规格的托盘弹药的布局分散,常用弹药和战备弹药的放置不合理等现象,这些因素对于弹药的快速高效保障都是不利的。当前,我军仓库中储存的箱装物资在垛位选择上还没有详细的方案,垛位的分配完全凭仓库业务人员的经验进行安排[1],在弹药的堆垛过程中,对托盘的选择以及垛位的顺序则很少考虑,垛位被随机排列,直接影响了收发作业的效率。鉴于此种现状,弹药库房中的集装模块垛位优化问题开展研究对提高作业效率,增强战时保障能力都具有重要意义。

2 弹药垛位优化模型

在实际的仓库储存过程中,不能保证一个仓库只对一种规格的弹药托盘进行堆放。这就面临着对一个仓库中多种规格的弹药托盘的堆放进行优化计算。既要确定一个仓库中摆放何种规格的弹药托盘,还要确定在该仓库中各个规格的托盘数量和堆码方式以及对不同弹药的使用频率和弹药的储备量来确定堆垛的位置,同时还要保证工作通道的宽度和位置设置的科学合理,从而使得每个垛位在收发过程中到门口的总路程L最短[2～3]。这样才能提高仓库的利用率和保障能力。

2.1 目标函数L

对整个弹药库房的储存布局优化来说,就是保证每个垛堆中所有弹药模块单元的作业路程最小。所以其目标函数L为

Lmin=[F1+F2+F3+…+Fi]

(1)

2.2 子目标函数Fi

为保证库房内每个垛位的托盘到门口的总路程最短,以仓库的一个角建立三维直角坐标系,设一个仓库中有l堆托盘,第i(i=1,2,3,…,l)堆垛中任一托盘的坐标为Vi=(x,i,y,i,z,i)m,n,g,距离函数Fi为第i堆中的所有托盘到门口的总路程。则:

(2)

其中,(i,m,n,g)表示第i堆的第m行,n列,g层的托盘。

2.3 各垛堆的权重系数

由于仓库中储存的弹药品种和储量不尽相同,且部队对不同弹药的需求量也不同。每一垛堆的弹药品种、批次相同,根据不同的收发频率和需求量设定第i堆的权重系数为Ki。垛堆的收发频率越高[4],其权重系数Ki就越大,说明该垛堆应该摆放在靠近门口和主通道的位置,以便于快速、高效的收发作业。

2.4 约束条件

在军用弹药仓库的存储布局中,影响路径优化的主要是通道的设置,如果通道的宽度和位置设置合理,就可以大大缩短作业路程和作业时间,提高作业效率。存储区的通道主要是用于出入库房作业的工作通道(包括机械搬运通道和手动叉车通道)和人员的检查通道[5]。主通道连接弹药仓储区的进出口和各作业区域,手动叉车通道是连接主通道和各垛堆的通道,一般平行或垂直于主通道,不应与库房墙壁临近,检查通道是相邻垛堆之间通道,用于对弹药的日常常规性检查[6]。

通道宽度设计根据不同作业区域、人员或车辆行走速度、单位时间按通行人数、搬运物品体积等因素而定。为了满足搬运机械的转弯半径和作业顺畅,设定作业面T作≥4.2m,叉车通道T叉≥1.8m,为方便库房的日常检查,设定检查通道T检≥0.6m,为了保证机械作业的安全,垛堆的顶高距天花板的距离D通常大于等于0.5m[7～10]。即约束条件为

(3)

这样才能保证机械搬运的顺利作业,完成收发任务。

2.5 归一简化处理

根据弹药库房的堆垛原则,同一批次的弹药和同一型号的托盘集中放置。在储存布局的确定中,由于垛堆的层数g对于垛堆位置的设定不产生影响,而且在确定了垛堆的位置后,层数g对于作业路程L的影响也比较小。因此,为了简化运算,将模型中堆垛层数设定为1层。

由式(2)可知,第i垛堆中的任一托盘坐标为Vi,因此Vi可简化为(xi,yi,1)m,n,1。对于垛堆中的每个托盘的坐标可进行归一化处理。由于每个垛堆的托盘的规格相同,所以垛堆的中心坐标V中为

(4)

进而可以得到Fi的简化

Fi=m*n*V中

(5)

即当确定了一个垛堆的托盘数和中心坐标后,便可以得到该垛堆所有集装单元的作业路程总值。

2.6 模型表示

综上所述,根据式(1)～式(5),弹药库的储存布局数学模型为

Lmin=[k1*F1+k2F2+k3F3+…+klFl]

约束条件:

(6)

3 遗传算法对实例问题的优化求解

3.1 选取算法类型

从上述模型建立过程中可以看出,对于弹药存储的集装模块优化问题是多目标优化问题,需要考虑多个目标函数的同时优化。根据本模型中的多目标优化,采用权重系数变换法来进行计算,根据各个垛堆不同的收发频率和需求量等因素综合设定权重系数Ki。将多目标优化问题化为单目标优化问题,进而求解多目标优化问题[11～12]。

3.2 实例计算

3.2.1 选定托盘规格

托盘是一种用于机械化装卸、搬运和堆存货物的集装单元工具,GJB184A-1999《军用立柱式托盘和箱式托盘基本尺寸和额定载重量》中规定了三种军用托盘标准尺寸,分别是800mm×1200mm、1000mm×1200mm和1100mm×1100mm。

设定一地面库长D=15m,宽W=10m,高为Z=5m,堆垛最多层数为G=3,为简化计算,选择规格为1200×1000×1300,1200×800×1300,1100×1100×1300的三种托盘来进行堆垛。为了保障堆码的顺利和收放作业的通畅,设定主作业面4.2m,检查通道0.6m,叉车通道1.8m。托盘的堆放按照弹药库房的堆放原则摆放,保证弹体与通风口方向一致[13]。其堆垛样式如图1所示。

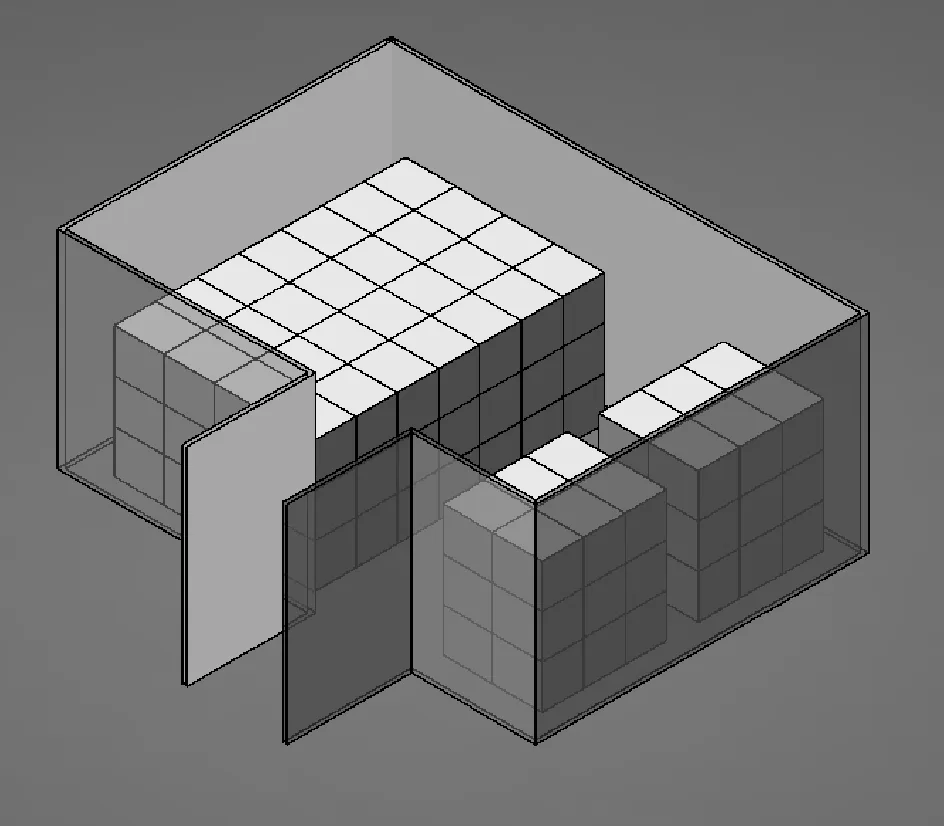
图1 地面库堆码效果图

3.2.2 数学模型表示

现对实例库房中的集装模块垛位优化模型进行数学表达。设地面弹药库有一个出入口,库房长15m,宽10m,高5m。现存三个垛堆,垛堆的托盘规格分别为:1200×1000×1300,1200×800×1300,1100×1100×1300三种。如图2所示。

图2 库房储存布局示意图

其中,各垛堆的权重系数k1=0.7,k2=0.5,k3=0.3。编号为①、②、③的托盘分别为三个垛堆的中心托盘,设其坐标分别为V1(x1,y1),V2(x2,y2),V3(x3,y3)。则目标函数为

Lmin=[k1F1+k2F2+k3F3]

(7)

约束条件:

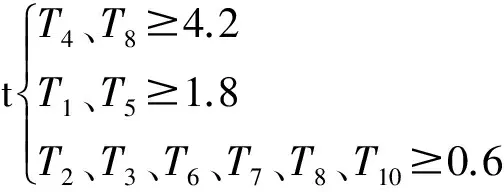
即:

Lmin=[k1F1+k2F2+k3F3]

(8)

3.3 具体算法步骤

· 第一步:编码

在遗传算法中最常用的编码方式为二进制编码,但是这种编码方式不能较好地适用于货位规划这个多目标优化分配问题[14]。由于约束条件为实数区间,所以本文采用十进制实数编码。染色体的编码采用顺序表达法,即根据集装模块单元的位置在库房中的顺序进行编码。设定库房中共有i个集装模块单元,每个单元的位置可以设定为(xi,yi),那么染色体的编码为[(x1,y1)(x2,y2)(x3,y3)(x4,y4)…(xi,yi)],其示意图如下:

X1，Y1X2，Y2X3，Y3X4，Y4……Xi，Yi

在运算过程中为保证计算的精度,可以将染色体编码转换为二进制进行计算,再对计算结果转换为十进制进行表示。

· 第二步:生成初始种群

根据约束条件,随机生成数量为N的初始种群,作为垛位优化的初始解。

· 第三步:适应度函数

根据目标函数Lmin=[k1*F1+k2F2+k3F3+…+kiFi]以及权重系数ki计算出每个集装模块单元的最短路径,因此,目标函数值越大,个体遗传到下一代的概率就越小,即适应度越小。为了满足目标值的优化要求,就要在选择之前将个体目标函数转化为适应值:

(9)

式中Cmax为一个适当的相对较大的数,这里定为L(x)的最大值。适应度函数的分配通过ranking函数计算,按照个体的目标值Lmin由小到大的顺序进行对它们进行排序,使用线性评估,给最适应个体的适应度值为2,最差个体的适应度值为0。

· 第四步:选择遗传算子

在选择遗传算子时采用选择比例算子。个体被选择的概率由式(10)给出,

(10)

其中P(xI)为这个个体被选择的概率,fi为个体的适应度值,∑fi为个体的适应度之和。

· 第五步:交叉、变异运算

在遗传算法中,通常随机选择两个个体进行交叉操作。通过交叉操作使得目标函数下的优良基因可以充分组合,以保证较大概率的找到目标函数的有化解。交叉概率的取值范围一般是:0.4～0.99。

变异运算决定了遗传算法的局部搜索能力。变异算子按照一定的概率(变异概率)选择部分个体的部分染色体进行变异,被选定的个体按照随机选择的两个垛位的位置进行相互对换,生成新的个体的同时又保持了种群的多样性。交叉概率的取值范围一般为:0.0001～0.1。

· 第六步:终止操作

遗传算法的终止操作有很多种,本文采用设定遗传的迭代代数。当遗传迭代代数达到设定数值后,自动停止计算。否则继续返回到第三步继续运算,直到到达设定代数为止[15]。

3.4 通过Matlab编程对优化解进行表示

根据本文中的实例设定,可以通过Matlab编程进行运算。设定初始种群NIND=100;最大遗传代数MAXGEN=50;代沟GGAP=0.9;交叉概率Px=0.7;变异概率Pm=0.02。计算50代后得到最优解如表2及种群均值变化的性能跟踪如图3所示。

表2 进化后的最优化解

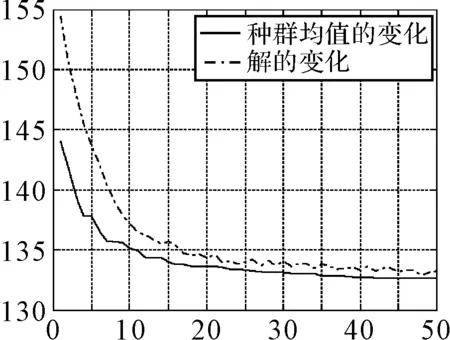
图3 种群均值变化性能跟踪图

4 结果

通过以上计算可以看出,随着遗传代数的增加,最优解有了明显的下降。经过50代的遗传进化,最优解从最初的139.5697将降为132.5724,降幅达到了5.01%。对于垛堆的位置坐标也得到了最优解:(x1,y1)=(3.9051,3.0000),(x2,y2)=(3.9020,4.3019),(x3,y3)=(3.7513,6.4618)。在优化进程中,库房中各个通道的宽度数据如表3所示,T3的初始值为0.0833,经过交叉变异30代后达到了0.4358,虽然有所提高,但仍不满足要求。在50代时达到了0.7118(大于0.6),满足了库房作业通道的基本要求。以上数据计算表明通过遗传算法该对解决垛位优化问题有较为明显的效果。

表3 优化后的通道数值

5 结语

本文通过对现有弹药仓库的集装化模块弹药垛位优化问题建立数学模型,选定合适规格的托盘,运用遗传算法对弹药仓库垛位布局进行实例优化计算,通过Matlab编程计算得出集装模块弹药垛堆的优化位置以及库房的作业通道设置,在计算过程中,随着遗传进化代数的增加,可以看出总路程明显的减少以及通道宽度的不断优化,最终实现了弹药跺位的优化,为提高仓库作业效率和弹药堆的合理布局提供了较为科学的依据。

[1] 冯涛,钟敬武.货位布局技术在后方仓库中的研究与实现[J].计算机技术与自动化,2006,25(4):293-295.

[2] 陶英歌,郭乃林,罗红英.基于遗传算法的目标分配优化模型研究[J].系统工程与电子技术,2003:817-819.

[3] 魏国辰.物流机械设备的运用与管理[M].北京:中国物资出版社,2002,1:173-190.

[4] 贺鑫,马振书,李良春,等.遗传算法在箱装军用物资垛位优化中应用[J].科学技术与工程,2011,11(1):93-94.

[5] 朱子音.提高库房利用率方法研究[D].长春:吉林大学硕士论文,2008:22-23.

[6] 刘昌祺.物流配送中心设施及设备设计[M].北京:机械工业出版社,2004,9:1-18,156-169.

[7] 李梅娟,陈雪波.Pareto遗传算法在货位配置中的应用研究[J].控制工程,2006:139-140.

[8] Stengel R F, Ray L R. Stochastic robustness of linear time-invariant systems[J]. IEEE Trans On Aut Control,1991,36(1):82-87.

[9] Ray L R, Stengel RF. AMont Carlo approachtothe analysisof control system robustness[J]. Automatica,1993,29(2):229-236.

[10] Carlos F M, Peter F J. An overview of evolutionary algorithmsin multiobjective optimization[J]. Evolutionary Computation,1995,3(1):1-16.

[11] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2011:45-61,107-118.

[12] 龚纯,王正林.精通MATLAB最优化计算[M].北京:电子工业出版社,313-315.

Ammunition Container Module Stacking Location Optimization Based on Genetic Algorithm

REN Junpeng YAN Ping TAN Bo

(Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033)

Stacking location optimization is an important content of ammuniction warehouse management. Firstly, this paper establishes the warehouse of the module ammunition container tatal moving distance and the heap stacking location usage frequency multi-objecctive optimization model. Then, the weight coefficient transform method of multi-objective genetic algorithm is used for optimization calculation with true instance, and the specific steps and the operating process are given. Finally, the warehouse of the actual size of 15m×10m×5m optimizations are calculated by Matlab, and the optimization solution down from 139.569 to 132.5724, reduced by 5.01% which have proved the effectiveness of the proposed method.

stacking location optimization, containers module, genetic algorithm

2015年6月13日,

2015年8月1日

任俊鹏,男,硕士研究生,研究方向:武器系统运用与保障工程。严平,男,博士,副教授,研究方向:武器毁伤效能与弹药设计。谭波,男,博士,讲师,研究方向:弹药工程。

TJ410.3

10.3969/j.issn.1672-9730.2015.12.030