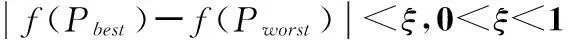基于改进遗传算法的虚拟装配路径规划研究

王光慧，胡赤兵，贺成柱

(1. 兰州理工大学，甘肃 兰州 730050； 2. 甘肃省机械科学研究院，甘肃 兰州 730050)



基于改进遗传算法的虚拟装配路径规划研究

王光慧1,2，胡赤兵1，贺成柱2

(1. 兰州理工大学，甘肃 兰州 730050； 2. 甘肃省机械科学研究院，甘肃 兰州 730050)

摘要：装配路径规划是虚拟装配技术的核心，为了获得最优装配路径，在凸四边形障碍物环境中，通过对初始种群选取方法的重新定义，保证了参加演化算法的每条染色体都是可行的，同时对传统遗传算法中的变异算子和杂交算子进行改进，提高了算法的有效性。最后实验证明将改进的遗传算法运用到机械式减速箱装配中可得到更优的装配路径。

关键词：路径规划；网状图；改进遗传算法；基因表；最短路径

0引言

虚拟装配在近几十年发展较快，作为虚拟装配核心的装配路径规划更是得到了国内外学者的广泛应用[1,2]。路径规划是指在虚拟环境中零部件在组装成产品时所应遵循的空间路径，就是寻找一条从起始点到目标点且避免与周围的障碍物相碰撞的避障路径以及如何使这条避障路径最短最优。

虚拟装配路径规划主要包括虚拟装配环境模型的建立和路径规划演化算法的设计。其中环境模型的建立目前应用较广的有栅格表示法[3]和最小多边形包围盒法[4]。栅格法中栅格大小的划分是个难题，栅格越小计算结果越精确，但需要大量的存储空间和搜索距离。本文用凸四边形包围障碍物，这样不仅可以消除由于顶点数目繁多而引起的算法效率低下，而且可以较精确逼真地描述障碍物空间。目前主要的路径规划演化算法有遗传算法[5]、蚁群算法[6]、模拟退火算法[7]、粒子群算法[8]、郭涛算法[9]等。其中遗传算法(GA)在多目标虚拟装配路径规划[10]和移动机器人路径规划[11]中得到广泛应用，但其初始种群都采用随机方式选取，这样使得计算量大，缺乏目的性，算法的收敛性也差。并且交叉算子和变异算子都是针对两条染色体进行，这样虽然可以在一定程度上提高了算法的收敛速度，但是容易陷入局部最优。为了解决此问题，本文提出了一种改进的遗传算法(IGA)，首先提出一种定义初始种群的全新有效方法，以基因表为条件，以网状图为方法，使得到的初始种群都是有效的，然后对选定的一条染色体进行变异杂交运算。本文以农业机械的机械式减速器为模型，研究其虚拟装配路径规划问题。

1空间环境的建立

1.1　装配环境建模

用凸四边形表示障碍物，并且将四边形放大一个目标物安全行走的距离，然后将三维障碍空间投射到二维平面上，形成如图1所示的装配环境地形图。

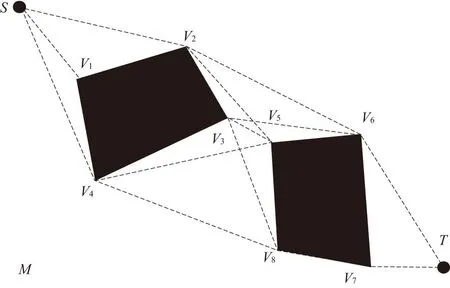
图1　环境地形图

定义：M表示障碍物环境空间，R={Ri∣i=1,2…}表示障碍物。为了编码方便，令障碍物的所有顶点以及起始点、目标点统称为顶点，按顺时针方向编码，以顶点集合V为编码空间，顶点集合为V={vi∣i=0,1,2,…,n}，其中v0表示起始点S，vn表示目标点T，(xi,yi)为顶点vi的坐标，vi-vj表示两顶点相连，四边形各边集合为E={ei∣i=1,2,…}。

1.2　编码方式

采用实数编码，因为实数编码是直接以解空间的形式进行编码，这样大大缩短了串长，扩大搜索域，对一些多维，高精度连续函数的优化问题同样适用。采用顺序表达方法，如：路径Pi={S,v2,v5,v6,T}表示从起始点S依次到顶点v2-v5-v6再到目标点T的一条路径，其中起始点S和目标点T的位置始终不变。

1.3　成本矩阵

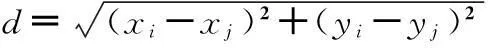
两顶点连线与多边形的边相交时，d=∞，两顶点相同时d=0。数学表达式为：

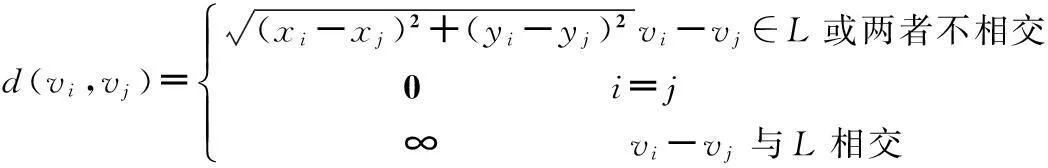
(1)

成本矩阵的计算式：

C[i][j]=d(vi,vj)

(2)

由式(1)和式(2)可得图1的成本矩阵为：

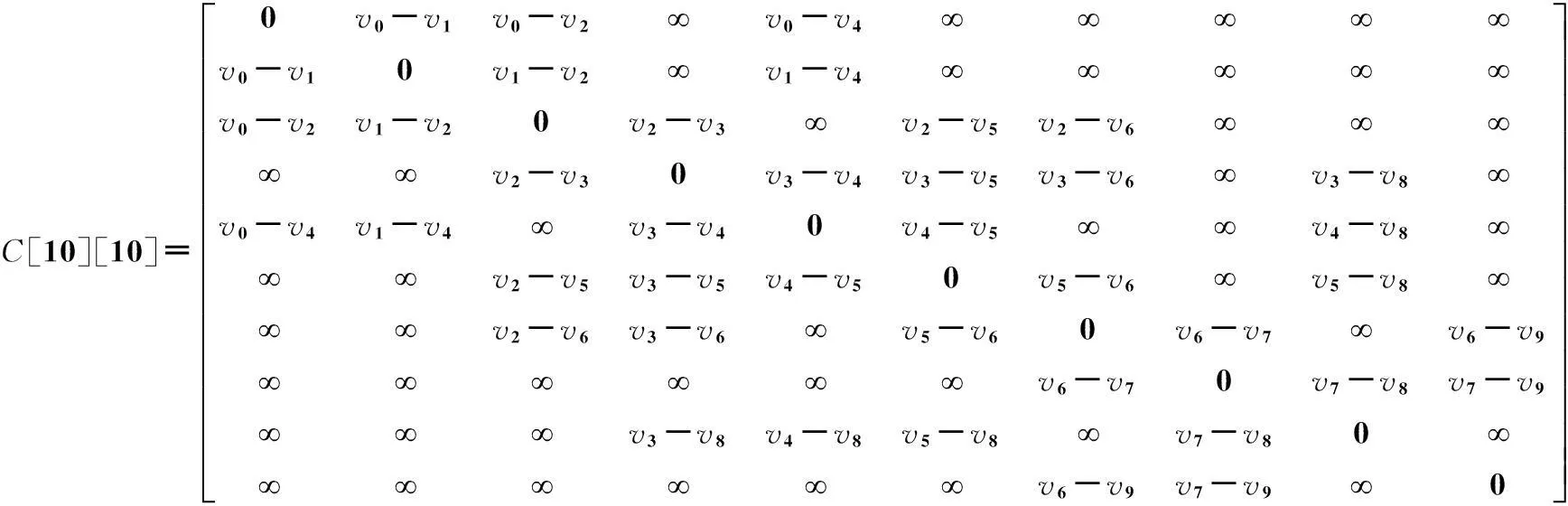
(3)

2算法设计

2.1　初始种群的选取

为了保证初始种群的有效性，避免引入非法路径，路径的选取必须满足一定的条件，将这些条件汇总成表格，在此命为条件基因表。如以成本矩阵(3)为基础提取信息，得图1中与各个顶点可相连的基因表，如表1所示。

表1　基因表

根据基因表从起点S到目标点T的初始路径应该满足条件：1)路径合法，不与障碍物相交；2)为了避免形成环路，与顶点vi相连的下一个顶点vj的位置应比vi到目标点T近。可用网状图2来表示初始种群的选择过程。

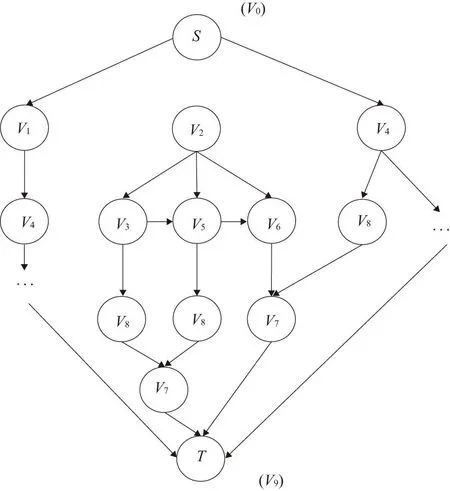
图2　网状图

图2中每一条由S到T的合理路径构成了初始种群P={Pi|i=1,2,…,N}，如Pi={v0,v2,v5,v8,v7,v9}。用此方法得到的初始种群，避免了以往用随机方法产生的无用染色体，让随后的算法在合理可行的染色体上进行，大大提高了算法的有效性，节省运算时间。当障碍物较少时初始路径的选取不是很庞大，可以直接用此方法搜索出最短路径，无需进行后续工作。

2.2　目标函数

本研究的目的是寻求最短装配路径，其目标函数是计算每条路径的长度，将一条路径的长度作为该路径的适应度函数，路径越短其适应度越好。适应度函数：

(4)

2.3　选择算子

用树形图法得到初始种群数量较多，为了提高算法的效率，从初始种群P中选择M条染色体构成解空间Q参加演化计算。具体方法是：根据式(4)求出P中每条染色体的适应度值f(Pi)，并从大到小排序，选取前M个适应度值较大的染色体构成Q={Qi|i=1,2,…,M}，P中剩余的染色体构成P’={Pi’|i=1,2,…,N-M}。本文选择适应性较差的个体进行演化算法，目的是为了防止P中适应性好的个体在演化过程中失去它的优越性。

2.4　变异算子

变异算子是对某些染色体的某一处基因进行替换，主要是针对适应性较差的个体进行。传统的变异操作是互换两条染色体中的某一个基因位，此处是针对一条染色体进行变异操作。具体为选择染色体Qi中的一个基因点ai，根据表1选出ai对应的下一个基因点为bi、ci…,并分别用bi、ci…替换掉Qi中ai的下一个基因点，计算各自的适应度值，求得适应度值最小的Qj，将Qj赋给Qi。依次进行，直到Qi中的每一个基因点都被取过。如染色体Qi={v0,v2,v3,v8,v7,v9}，若先选定基因点v2，由表1得v2点的下一个基因点分别为v3、v5、v6，替换得Q1j={v0,v2,v5,v8,v7,v9}，Q2j={v0,v2,v6,v8,v7,v9}，计算f(Q1j)

变异概率Pm的选取关系到该条染色体是否进行变异操作，本文定义Qi的变异概率为：

(5)

2.5　交叉算子

交叉概率Pc越大，可以越快收敛到希望的最优解区域，因此一般选取较大的交叉概率，但太大的交叉概率也可能导致早熟现象，一般取0.4~0.9。当Pc<λ(0<λ<1)时进行交叉运算。运算刚开始主要是交叉算子在起作用，所以选取的交叉概率较大，随着计算的进行，为了保持算法的稳定性交叉，概率的取值会相应的减少。

2.6　停机条件

传统的停机条件有，达到了最大进化代数、收敛标准、时间标准和精度标准等。本文采用收敛准则，即：

(6)

当适应度函数的值趋于稳定时，运算结束。

3算法流程图

在设计完该算法后，需要按照一定的流程对算法进行实施，以实现对装配路径的规划。首先是装配环境模型的建立，将障碍物用凸四边形表示并放大一个安全距离，按顺时针对各顶点采用实数编码构成图1所示的装配环境，然后计算各点的成本矩阵C。重要的是通过成本举证提取基因表，以基因表为条件，按照网状图法随机选出N个染色体，再从N个染色体中选出M个形成种群P，参加IGA演化计算。根据算法设计得到的具体操作流程如图3所示。

图3　改进遗传算法流程图

4实验分析

如何让指定的零部件绕开障碍物快速地安装到指定的位置是虚拟装配路径规划的难点，也是最终目的。例如DELMIA软件采用可拆即可装的原理完成对零部件的装配，主要依靠人的经验，无法保证所规划的装配路径是最优最短的。

为了验证改进遗传算法的优越性，以农业机械的机械式减速器为模型，将改进的遗传算法和传统的遗传算法在计算机上运行40次得到图4所示的结果，其中定义P=100，M=80，pc=0.7。从图4中可以明显得到改进的遗传算法在运行了17次之后就基本趋于收敛稳定，而传统遗传算法在运行40次之后才开始收敛到最优解，说明改进的遗传算法大大提高了传统遗传算法的收敛性。

图4　IGA与GA收敛性对比

IGA与GA的收敛性对比可知IGA在运行20次之后可趋于稳定。为了进一步说明改进遗传算法在虚拟装配路径规划中的优越性，将其与传统遗传算法运行20次得到图5所示的路径规划图。定义P=100，M=80，pc=0.7。其中用IGA所的路径长为15.246m，途经4个障碍物；用GA所得路径长28.562m，途经9个障碍物。改进的遗传算法在运行相同次数下所得的路径短，经过的障碍物少，所以更容易得到装配件的最佳装配路径。

图5　IGA与GA路径规划对比

5结论

本研究为了更好更快地得到最佳的装配路径，以凸四边形障碍物为装配环境，对初始种群选取方法重新定义，通过成本矩阵提取基因表并依此为条件建立初始种群，保

证了参加演化算法的每条染色体都是可行的。同时改进了传统GA中的变异算子和杂交算子。最后实验证明改进后的IGA的收敛速度、动态收敛性和计算效率比遗传算法好。以顶点作为基因点所得到的路径都是直线段不够平滑，应该对所得到的路径进行平滑处理，本文中没有涉及，以后会继续完善。IGA不仅可以用于虚拟装配路径规划，在对机器人避障路径规划中同样适用，可以应用于未来智能装配及路径规划。

参考文献:

[1] R. G. Dewar, I. D. Carpenter, J.M. Ritchie, J. E. L. Simmons, “Assembly planning in a virtual environment,” International Conference on Management and Technology, July 1997, pp. 664-667.

[2] A. Seth,J. M. Vance, J. H. Oliver, “Virtual reality for assembly methods prototyping: a review,” Virtual Reality, 2011, pp. 5-20.

[3] A. Elfes, “Using occupancy grids for mobile robot perception and navigation,” Computer, vol. 22, Issue 6, June 1989, pp. 46-57.

[4] T. Simeon, S. Leroy, J. P. Lauumond, “Path coordination for multiple mobile robots: a resolution-complete algorithm,” Robotics and Automation, IEEE Transaction, vol. 18, Issue 1, 2002, pp. 42-49.

[5] A. Elashmli, H. A. Abdullah,S. Areibi, “Genetic algorithm for dynamic path planning,” Electrical and Computer Engineering, 2004. Canadian, vol. 2, May 2004, pp. 677-680.

[6] Tan Guan-zheng, He Huan, Sloman Aaron. Ant Colony System Algorithm for Real-Time Globally Optimal Path Planning of Mobile Robots. Acta Automation Sinica, 2007,33(3)：007-0279.

[7] S. Kirkpatrick, C. D. Gelatt, M. P. Vecchi, “Optimization by Simulated Annealing,” Science, New Series, vol. 220,May 1983, pp. 671-680.

[8] M. Saska, M. Macas, L. Preucil, L. Lhotska, “Robot path planning using particle swarm optimization of Fergusion splines,” Emerging Technologies and Factory Automation, 2006. ETFA’06. IEEE Conference, Sept. 2006, pp. 833-839.

[9] 戴光明. 避障路径规划[D]. 武汉：华中科技大学博士生学位论文，2004,4.

[10] F. Tao, K. Qiao, L. Zhang, Z. Li, “GA-BHTR: an improved genetic algorithm for partner selection in virtual manufacuring,” International Journal of Production Research, vol. 50, Issue 8, 2012, pp. 2079-2100.

[11] F. Ahmed, K. Deb, “Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms,” Soft Computing, July 2013, vol.17, Issue 7, pp. 1283-1299.

[12] 张超群，郑建国，钱洁.遗传算法编码方案比较[J]. 计算机应用研究，2011,28(3).

Study of Virtual Assembly Path Planning Based on Improved Genetic Algorithm

WANG Guang-hui1,2, HU Chi-bing1, HE Cheng-zhu2

(1. Lanzhou University of Technology, Lanzhou 730050, China;

2. Mechanical Engineering Research Institute of Gansu Province, Lanzhou 730050, China)

Abstract:Assembly path planning is the core of virtual assembly. In order to obtain the optimal path, an improved algorithm based on genetic algorithm is proposed in the convex quadrilateral obstacle environment. The selection of the sample population is redefined to make sure that all the chromosomes involved in the evolutionary algorithms are useful. And the traditional mutation operator and crossover operator of genetic algorithm are improved to enhance the efficiency of the algorithm. Experiment shows that the mechanical reducer can be used to optimize the assembly path.

Keywords:path planning; nelwork chart; improved algorithml; genetic list; shortest path

收稿日期：2013-09-11

中图分类号：TP301

文献标志码：A

文章编号：1671-5276(2015)01-0205-04

作者简介：王光慧(1987-)，女，甘肃兰州人，硕士研究生，研究方向为数字化制造。

基金项目：“十二五”国家科技支撑计划资助项目(2011BAD20B01)