部分相干双曲余弦-高斯光束通过像散透镜的光束参数变化

李长伟,冯 浩

(琼州学院 理工学院,海南 三亚 572022)



部分相干双曲余弦-高斯光束通过像散透镜的光束参数变化

李长伟,冯 浩

(琼州学院 理工学院,海南 三亚 572022)

研究了部分相干双曲余弦-高斯(ChG)光束通过像散透镜的光束参数变化,并对像散和空间相干参数对束宽、束腰位置及远场发散角的影响做了重点分析.结果表明,受像散影响,部分相干ChG光束在x、y方向束宽、束腰位置和远场发散角表现不同;束宽相对误差随空间相干参数的增大而增大,在几何焦面两侧出现一大一小两个峰值;在几何焦面处,x、y方向的束宽相对误差变化规律相同;x方向远场发散角相对误差随像散的增大而增大,当达到峰值之后进而随像散的增大减小;y方向远场发散角相对误差随像散增大近似呈线性增大.

部分相干双曲余弦-高斯光束；像散；相对误差

部分相干光的传输和变换规律,有重要理论和现实意义[1-2].对于实际的成像系统而言,傍轴条件常常不能满足,点物形成一弥散斑,物体不能生成清晰的像.当光束在非轴对称光学系统中传输时,会产生像散[ 3-4].厄米正弦类高斯光束,如双曲正(余)弦高斯光束等是在近轴近似下波动方程的解[5],对厄米正弦类部分相干光通过理想光学系统的研究较多,但对其通过有像差光学系统的研究较少[6-7].因此分析研究像散对部分相干光光束参数的影响具有实际应用意义.本文以部分相干双曲余弦-高斯(ChG)光束为例,对其通过像散透镜后的光束参数变化做了深入研究,重点分析了空间相干参数和像散对束宽、束腰位置、束腰宽度以及远场发散角相对误差的影响,并作了数值计算和讨论.

1 理论模型

部分相干ChG光束在入射面z=0处,可用交叉谱密度函数表示为[8]

(1)

其中:空间相关长度表示为σ,入射光束高斯部分束腰宽度对应为w0,Ω0为与双曲余弦项有关的参量,I0为一光强常数.

设z=0处有一像散透镜,焦距为f,由于像散引入的相位因子可表示为[4]

exp[-ikC6(x′2-y′2)]，

(2)

式中,k为波数,且k=2π/λ,C6为像散系数.将上述两式代入部分相干光的传输公式,经过繁冗积分,得部分相干ChG光束通过像散透镜后在出射面z处的光强为[7]

(3)

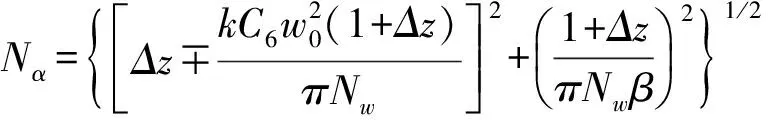
(4)

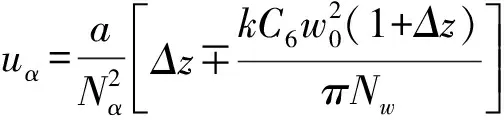
(5)

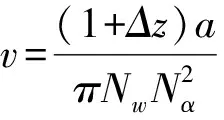
(6)

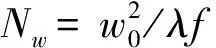
(7)

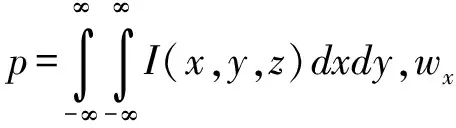
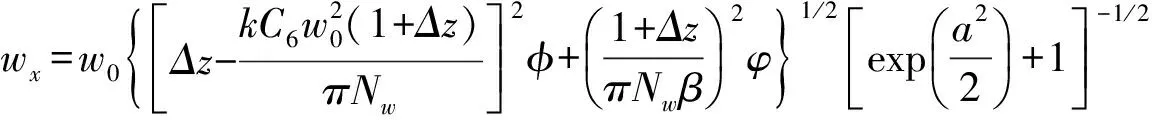
(8a)

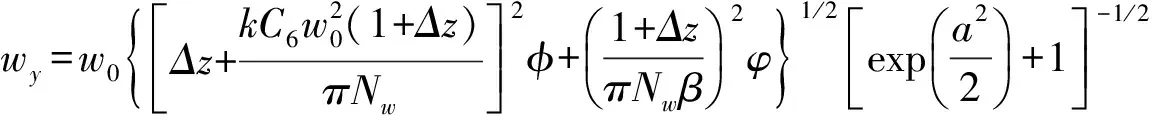
(8b)

令C6=0,由(8)式可得部分相干光束ChG通过理想无像散透镜的束宽

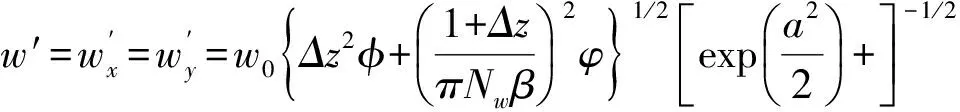
(9)

部分相干ChG光束通过像散透镜后的束宽相对误差表示为[10]

(10)

将(8)、(9))式代入上式,整理可得出射面处x、y方向束宽的相对误差为

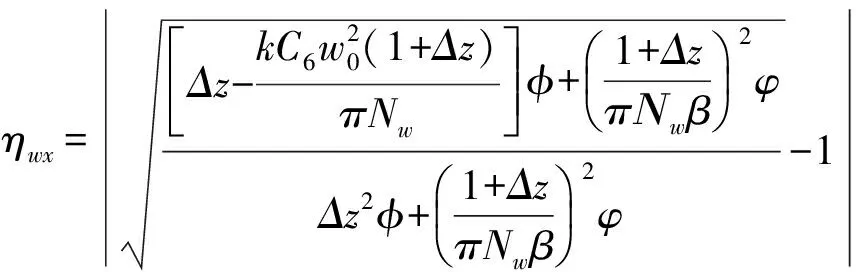
(11a)

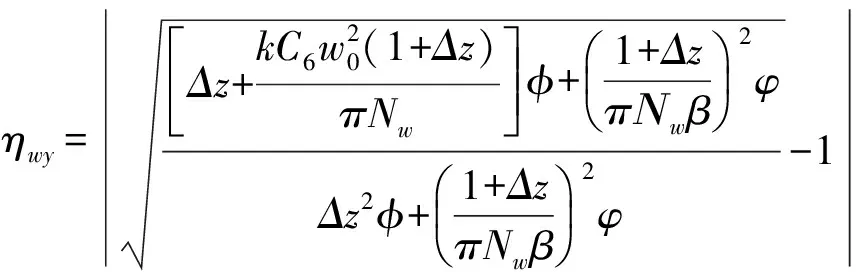
(11b)

上式表明,x、y方向束宽的相对误差变化取决于离心参数a,像散系数C6,空间相干参数β、菲涅耳数Nw以及传输距离z,且像散使得x、y方向束宽相对误差出现差异.将z=f代入(8)和(11)式,分别可得几何焦面处x、y方向的束宽公式及束宽相对误差公式为

(12)

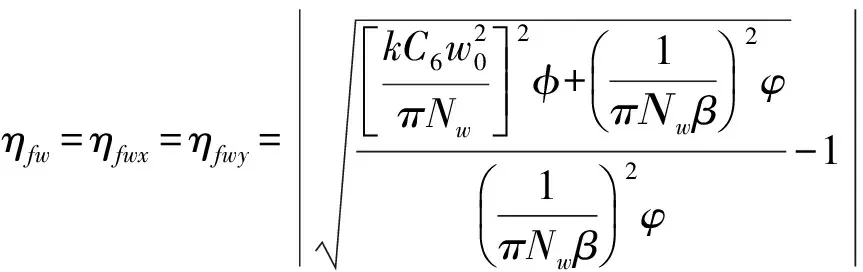
(13)

由∂wx/∂z=0,求得x方向束腰位置

(14a)

类似地,y方向束腰位置为

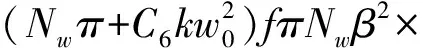
(14b)

(14)式表明,x方向和y方向束腰位置受像散的影响不再重合.对于理想透镜C6=0,有

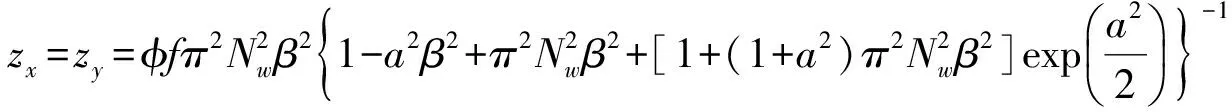
(15)

由(8)和(14)式得x、y方向束腰宽度为

(16a)

(16b)

x、y方向的远场发散角可分别求得为[11-12]

(17a)

(17b)

对于理想透镜,有

(18)

远场发散角的相对误差可表示为

(19)

将(17)、(18)式代入(19)式,分别可得部分相干光束ChG光束x、y方向远场发散角的相对误差为

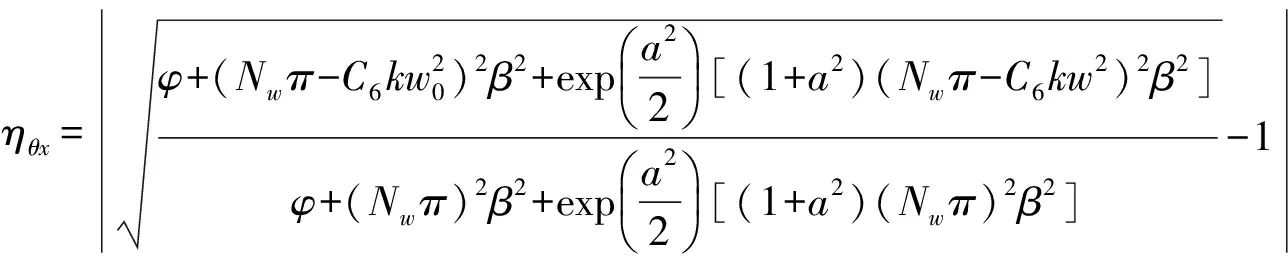
(20a)

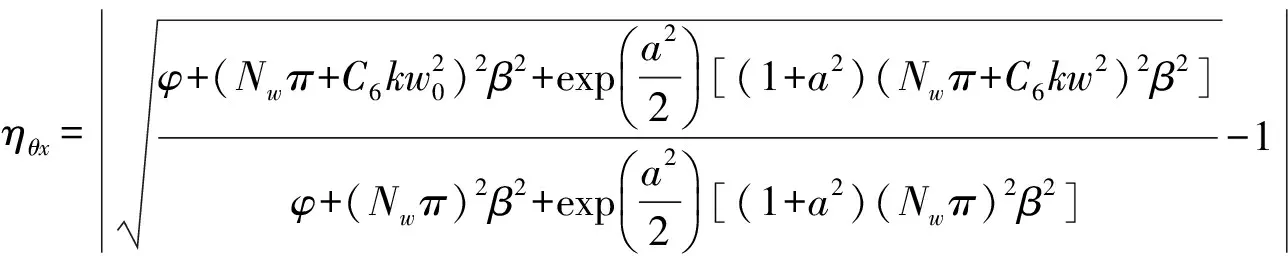
(20b)

(20)式表明,x、y方向远场发散角相对误差受像散的影响表现不同,且随离心参数a,像散系数C6,空间相干参数β的不同取值发生变化.

2 数值计算与讨论

以下数值计算中取部分相干ChG光束λ=1.06μm,w0=1 mm,f=200 mm.图1为不同空间相干参数β的部分相干ChG光束通过像散透镜后,x、y方向束宽相对误差ηwx,ηwy随传输距离z的变化.图中参数为：a=1,C6=1×10-4mm-1.由图1知,束宽相对误差随空间相干参数的增大而增大,且随传输距离发生变化.在几何焦面两侧出现一大一小两个峰值.在远离几何焦面处,相对误差随空间相干参数的变化并不明显.

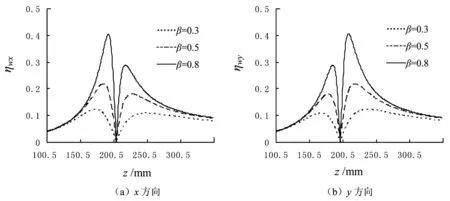
图1 空间相干参数β取不同值时x、y方向束宽相对误差ηwx，ηwy随传输距离z的变化

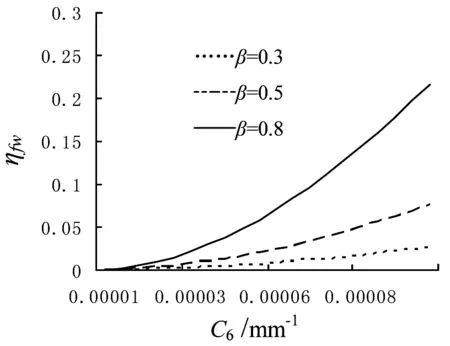
图2 空间相干参数β取不同值时几何焦面上束宽相对误差ηfw随像散系数C6的变化

图2为透镜几何焦面处空间相干参数取不同值时束宽相对误差ηfw随像散C6的变化.由图可知x方向和y方向的相对误差变化规律相同,与文中(13)式对应,几何焦面处x、y方向束宽相对误差ηfw随像散系数增大而增大,且随空间相干参数的增大而增大.

图3为空间相干参数取不同值时远场发散角的相对误差ηθx,ηθy随像散的变化曲线.图3表明, 图3为空间相干参数取不同值时远场发散角的相对误差ηθx,ηθy随像散的变化曲线.图3表明, 受像散的影响,x、y方向远场发散角的相对误差一般不相等,表现出差异,且偏差程度受相干参数的影响.x方向相对误差随像散的增大而增大,当达到峰值之后进而随像散的增大减小.y方向相对误差随像散增大近似呈线性增大.

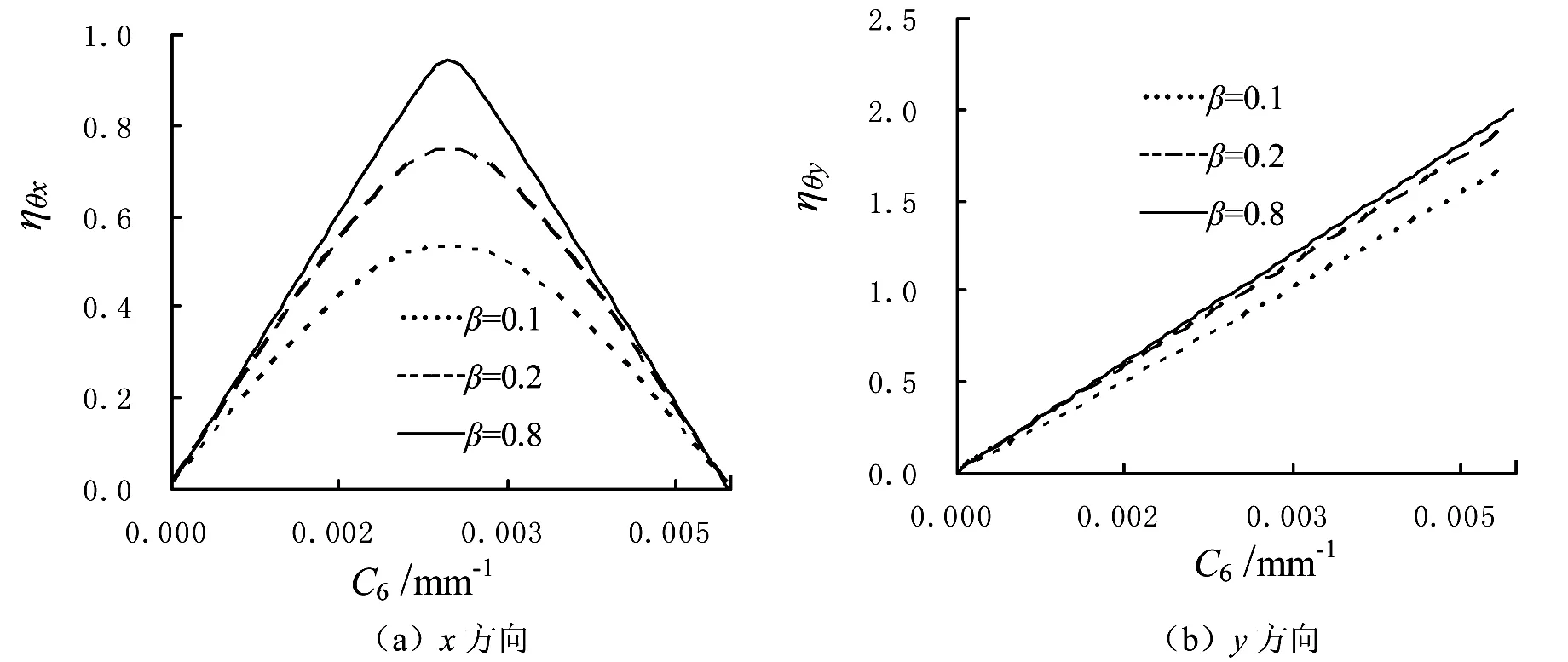
图3 空间相干参数β取不同值时远场发散角的相对误差ηθx，ηθy随像散系数C6的变化

3 结语

本文以部分相干ChG光束为例,推导出其通过像散透镜后的束宽、束腰位置、束腰宽度、远场发散角等,并详细研究了其通过像散透镜后光束参数的变化.像散使部分相干ChG光束在x和y方向束宽、束腰位置和远场发散角不同.束宽相对误差随空间相干参数的增大而增大,在几何焦面两侧出现一大一小两个峰值.在几何焦面处,x方向和y方向的相对误差有相同的变化规律,相对误差随像散系数增加而变大,随空间相干参数的增大而增大.x方向远场发散角相对误差随像散的增大而增大,当达到峰值之后进而随像散的增大减小.y方向远场发散角相对误差随像散增大近似呈线性增大.数值计算表明,束宽及远场发散角相对误差亦受离心参数的影响,且随离心参数的增大而增大,波形不发生变化.本文从光束空间相干性及像散两个方面对光束相对误差做了分析研究,对部分相干光通过像散透镜的光束变化有了进一步的认识,所得结果对设计合适的激光光学系统有实际应用意义.

[1]Mandel L, Wolf E.Optical Coherence and Quantum Optics[M].Cambridge: University Press, 1995.

[2]Goodman J W.Statistical Optics[M].New York: Wiley & Sons Press, 1985.

[3]Welford W. T.Aberrations of the Symmetric Optical System[M].NewYork: Academic, 1974.

[4]Alda J, Alonso J, Bernabeu E.Characterization of aberrated laser beams[J].J Opt Soc Am A, 1997, 14(10):2737-2747.

[5]Casperson L W, Hall D G, Tovar A A. Sinusoidal-Gaussian beams in complex optical systems [J].J Opt Soc Am A, 1997, 14(12):3341-3348.

[6]李长伟，康小平，何仲.部分相干双曲正弦：高斯光束的传输特性[J].琼州学院学报,2014，21(2):44-48.

[7]Pan L Z, LÜ B D.Focusing properties of partially coherent light passing through an astigmatic lens [J].Laser Technology, 2003, 27(4):374-379(in Chinese).

[8]Li C W, LU B D.Transformation and spatial shaping of partially coherent cosh-Gaussian beams through an astigmatic lens[J].Optik, 2009,120(5):374-378.

[9]Zahid M, Zubairy M S.Directionality of partially coherent Bessel-Gauss beams[J].Opt Commun, 1989, 70 (5):361-364.

[10]Siegman A E.New development in laser resonator[J].SPIE,1990, 1224:2-14.

[11]孟祥龙, 聂义友, 吕百达. 像散透镜对双曲余弦-高斯光束参量的影响[J].激光技术, 2008,32(1):53-56.

[12]吕百达.激光光学[M].北京：高等教育出版社,2003.

Changes in The Beam Parameters of Partially Coherent Cosh-Gaussian Beams after The Passage Through An Astigmatic Lens

LI Chang-wei, FENG Hao

(College of Science and Technology, Qiongzhou University, Sanya Hainan 572022, China)

The changes in the beam parameters of partially coherent cosh-Gaussian (ChG) beams through an astigmatic lens are studied and the effect of astigmatism and spatial coherence parameter on the beam widths, waist positions and far-field divergence angles are stressed. The results show that the astigmatism in a difference between the beam widths, waist positions and far-field divergence angles in thexandydirections. Relative errors of the beam widths increases with the coherence increases and take on a large and a small peaks on both side of the geometrical focal plane. Relative errors of the beam widths in thexandydirections have the same variation at the geometric focal plane. Relative errors of the far-field divergence angles in thexdirection increases as the coherence increases but decreased after the peak value. In theydirection, relative errors of the far-field divergence angles Increases linearly with the increase of astigmatism.

partially coherent cosh-Gaussian (ChG) beam; astigmatic; relative errors

2014-12-09

三亚市院地科技合作项目(2014YD28)

李长伟(1981-),男,河南平顶山人,琼州学院理工学院讲师,研究方向为激光传输与变换.

O435

A

1008-6722(2015) 02-0052-05

10.13307/j.issn.1008-6722．2015．02．12