输电线路地线融冰的热平衡分析与计算

李铁鼎，李健，吕健双，黄欲成

(中南电力设计院，武汉市 430071)



输电线路地线融冰的热平衡分析与计算

李铁鼎，李健，吕健双，黄欲成

(中南电力设计院，武汉市 430071)

根据我国电网覆冰的现状，结合国内外融冰的实践经验，在分析地线融冰机理的基础上，结合传热学的原理，建立椭圆融冰的数学计算模型，从工程应用的角度出发，研究最小融冰电流的计算方法。通过计算LBGJ-100-20AC、LBGJ-120-20AC、LBGJ-150-40AC这3种铝包钢绞线的地线融冰电流，分析覆冰厚度、风速、环境温度以及融冰时间等因素对地线融冰的影响；计算不同地线材料与融冰电流的关系；最后，通过该文提出的计算模型计算目前输电线路工程常用地线材料的最小融冰电流。计算结果与目前工程应用较多的布尔斯道尔夫融冰电流计算公式对比，发现2种方法的计算结果吻合较好。分析计算结果表明：在架空输电线路直流融冰过程中，融冰电流是由覆冰厚度、环境温度、风速和地线材料等参数共同决定，其中，环境温度、覆冰厚度和地线材料对地线短路电流融冰均有显著影响，但风速的影响相对较小。该文提出的融冰电流计算模型，为输电线路地线融冰电流的选择及融冰装置的设计，提供了有效的参考。

输电线路；地线融冰；热平衡；椭圆融冰模型；工程应用

0 引 言

覆冰这一特殊的气象条件曾给世界各地架空输电线路的安全运行造成严重影响。美国、加拿大、俄罗斯、法国和日本等国都曾发生严重冰雪事故[1]。我国受大气候和微地形、微气象条件的影响，系统冰闪跳闸和倒塔断线等冰灾事故也频繁发生。尤其是2008年初，我国南方出现大面积降雪[2]，低温雨雪冰冻灾害造成湖南、江西、贵州等省(区、市)输电线路严重受损,众多骨干输电线路被迫长期停运，电网稳定运行和电力可靠供应受到巨大的挑战，输电线路的融冰已成为我国电网的一个重要课题，

前苏联自上世纪50年代起开始应用交流短路融冰技术，加拿大自1993年起研究直流短路融冰。关于线路融冰电流和融冰实践的计算模型国内外也开展了许多研究，提出了多种融冰计算模型，如融冰动态模型、融冰静态模型、椭圆融冰模型等[1,3]。同时，随着计算机仿真技术的应用和发展，建立覆冰导线的物理数学模型[4-7]分析短路电流融冰的物理过程，通过融冰模型对短路融冰过程中导线温度、冰层变化等动态参数进行仿真。但是，物理仿真模型的建立过程较复杂，需要根据不同输电线路的覆冰情况、气象条件，地形及线路运行情况等建立不同的模型，且计算量很大，不便于工程应用实施。

近几年来，我国输电线路的融冰技术得到了快速的发展，采用目前的融冰装置，导线的融冰效果非常显著[1,8-9]，但是，架空地线由于自身的特点，比如分段接地或逐基接地、绝缘水平低等，其融冰方式不同于导线。若无法对地线进行融冰，导致地线发生滑移，可能会造成线路的跳闸停运。在不同融冰方案中融冰电流的选择是地线能否有效融冰的关键。本文主要研究满足地线融冰的最小融冰电流的计算方法，提出基于热平衡原理的椭圆融冰模型，分析其融冰过程及其影响因素，并计算得到目前输电线路工程常用地线材料的最小融冰电流，对输电线路地线融冰设计提供有效参考。

1 地线融冰的基本理论

1.1 融冰热平衡方程

假设地线为无限长导体，由于地线覆冰的截面形状与风速和风向、过冷却水滴的大小、地线的刚度等因素有关，十分复杂，本文将复杂的地线覆冰形状等效为圆柱形。根据实际工程经验，地线融冰过程中会形成椭圆形空气间隙，如图1所示。融冰电流产生的焦耳热，通过地线传递至冰层，在冰表面与空气进行热交换。融冰过程中，在重力作用下，地线上方的冰层逐渐融化，地线下方的气隙逐渐增长，椭圆面积也就不断增大直至覆冰脱落。整个融冰过程中Tc，T0，Ti和Ta分别表示地线表面温度，冰层内表面温度，冰层外表面温度和环境温度。

文献[10-12]基于热传递的基本原理，提出了覆冰导线融冰的热平衡微分基本方程如式(1)所示。

(1)

图1 地线融冰热平衡示意图

式中：I为融冰电流，A；rt为温度为T时导线的电阻率，Ω/m；Ri为覆冰导线的半径；h为冰层外表面与环境对流传热和辐射散热的热交换系数[8]，W/(m2·K)；TГ01为冰层外表面Г01的温度， ℃；Lc为导线的长度，m；dVm为融冰体积增量，m3；LF为冰融化时吸收的潜热，LF=335 000 J/m3；ρθk为区域θk的密度，kg/m3；Vθk为区域θk(k=1,2,3,4)的体积，m3，为融冰时间的函数；Cθk为区域θk的比热容，J/(kg·℃)；dTθk为区域θk的温度升高， ℃，融冰过程中导线、冰层及气隙的温度分布Tθk(x,y,t)(k=1,2,3,4)是时间和空间的函数。

1.2 融冰时间和融冰电流的计算

虽然地线融冰与导线融冰形式不同，运行状态也不一样，地线短路融冰跟导线短路融冰都是基于短路电流产生的焦耳热使覆冰融化脱落，地线融冰热平衡过程与导线融冰基本一致。与导线融冰不同的是，由于线路运行时地线只有感应电流产生焦耳热，电流很小几乎可以忽略，整个热平衡过程不需要考虑运行状态下地线温度对地线融冰的影响，因此，根据前面的热平衡微分方程分析可得：

(2)

式(2)考虑了地线融冰过程中3种主要消耗[8]：融冰过程中吸收的潜热；冰层外表面Г01的对流和辐射散热；地线、冰层吸热。

式(2)中：Dc为裸地线直径，m；di为覆冰厚度，m；h为散热系数，W/(m2℃)；Ti为冰层的温度；Vm为冰融化的体积，m3；Vc、Vi分别表示地线和冰层的体积，m3；ρc、ρi分别表示地线和冰层的密度，kg/m3；Cc、Ci分别表示地线和冰层的比热容，J/(kg℃)。忽略地线温度变化吸收的热量，冰层温度Ti取内外表面的平均温度，融冰时间和融冰电流的计算公式可以分别表示为

(3)

(4)

式(3)和(4)中涉及中间变量融冰体积Vm和冰层表面温度Ti，分别求解如下。

(1)融冰体积Vm。

冰层融冰脱落时刻融冰地线的截面图如图2所示，冰层融化的体积Vm即为椭圆形气隙的体积，即

(5)

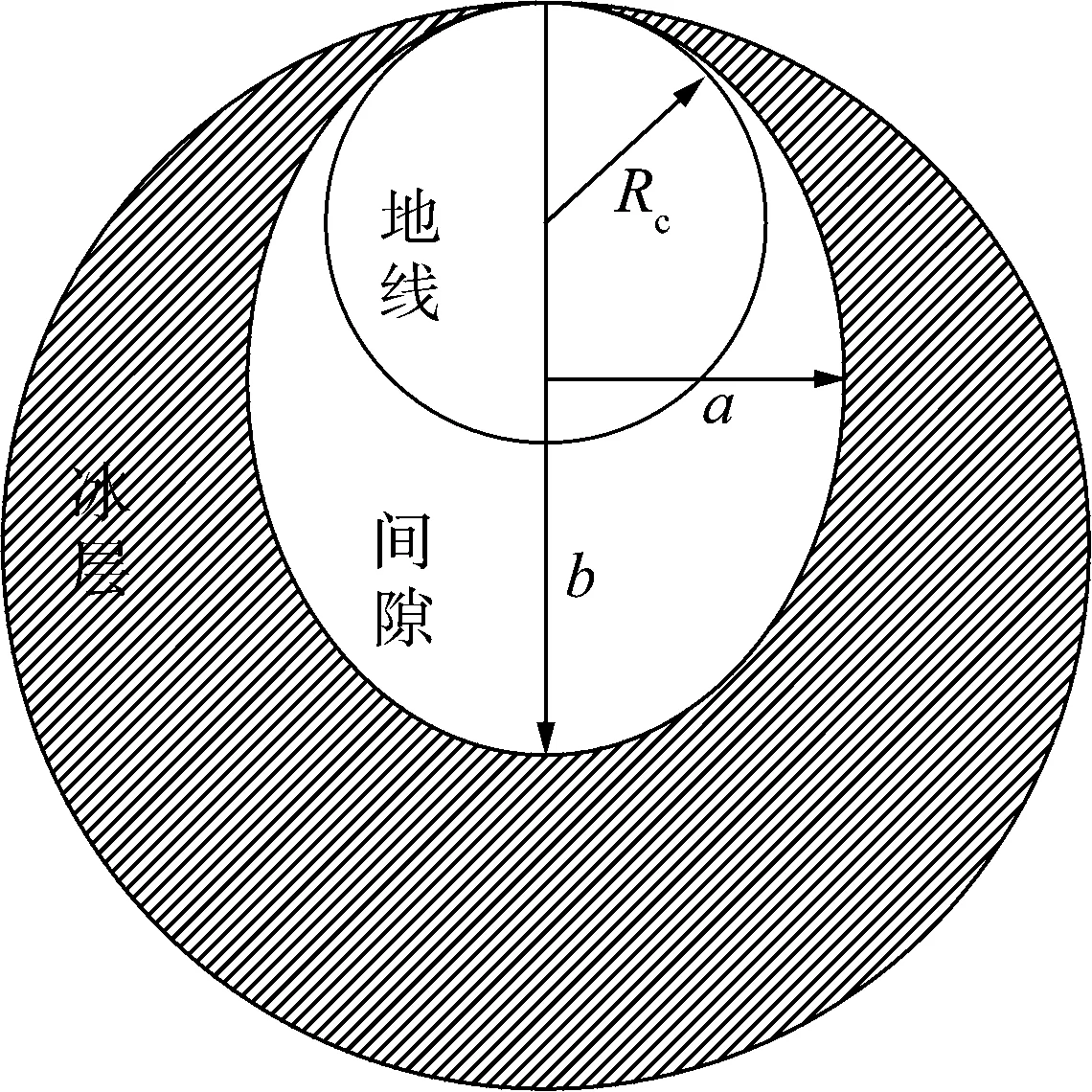
图2 脱落时刻融冰地线的截面图

根据地线外表面的圆必须内切于椭圆气隙这一约束条件，可得椭圆气隙的长轴b和短轴a必须满足以下关系：

(6)

(7)

忽略图2中地线下表面融化的冰层，得椭圆形气隙的长轴：

(8)

因此，融冰体积可以表示为

(9)

冰层的体积Vi可以表示为

(10)

(2)热交换系数h。

在融冰过程中，冰层外表面通过对流传热和辐射传热的方式向周围环境散热，散热系数为

(11)

式中：空气的传热系数λa=0.024 4 W/(m℃)；冰层外表面的发射率ε=0.95；Stefan-Boltzmann常量=5.67×10-8W/m2；另外，Re，Pr和Nu分别为雷诺数，普朗特数和努塞尔；Dc为地线直径，m；di为覆冰厚度，m；va为风速，m/s；v为空气的运动黏度，v=1.328×10-5m2/s；a为空气的热扩散率，a=1.88×10-5m2/s；C和n均为系数，对于覆冰天气，C=0.683，n=0.466[8]。

(3)冰表面温度Ti。

在冰层的外表面，热平衡方程如式(12)：

(12)

式中Rq为冰层的热阻[3]，即

(13)

由式(12)可解得：

(14)

最终得到融冰时间和融冰电流的计算公式。

把式(9)、(10)和(14)代入式(3)和(4)并化简得：

(15)

(16)

(17)

(18)

2 地线融冰电流及其影响因素

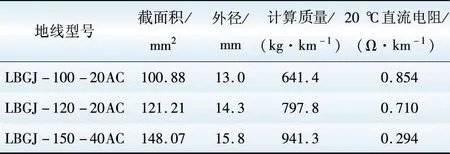
根据我国不同电压等级输电线路设计中常用的地线型号[16]，本文选择LBGJ-100-20AC、LBGJ-120-20AC、LBGJ-150-40AC这3种铝包钢绞线地线进行分析计算(参数见表1)。应用前面推导结果对地线融冰电流进行计算，除变化条件时，外界温度取-5 ℃、风速取5m/s、融冰时间取1h。

表1 地线基本参数(铝包钢绞线)

Table 1 Basic parameters of ground wire (Aluminume clad steel wire)

2.1 融冰电流与覆冰厚度的关系

融冰量的多少直接影响融冰电流大小及融冰时间的长短，本文研究1～20 mm覆冰情况下的融冰电流，计算结果如图3所示。

注：外界温度为-5 ℃；风速为5 m/s；融冰时间为1 h。

计算结果表明：覆冰厚度di对融冰电流影响很大，随着覆冰厚度的增加，融冰电流基本呈线性增加。覆冰每增加5 mm，LBGJ-100-20AC和LBGJ-120-20AC地线分别需增加融冰电流约25～31A，而直流电阻较小的LBGJ-150-40AC地线需增加约48～60 A。由于覆冰厚度增加快，且融冰需要一定时间，因此，通过覆冰预警装置，观测到架空地线覆冰厚度大于5 mm时，运行部门应考虑启动融冰装置，以免无法提供所需的融冰电流。

2.2 融冰电流与环境温度的关系

根据前面热平衡分析，冰层外表面的对流和辐射散热是影响融冰电流的主要因素之一，因此融冰电流与环境温度Ta的关系不可忽视，在覆冰厚度di，风速va，融冰时间t一定的情况下，冬季环境温度在-5～5 ℃条件下融冰电流计算如图4所示。

图4计算结果表明：环境温度Ta对于融冰电流影响较大，对于本工程采用的3种地线环境温度每下降2 ℃，LBGJ-100-20AC和LBGJ-120-20AC地线分别需增加融冰电流11～15 A，而LBGJ-150-40AC地线变化趋势较快一些，需增加融冰电流25～30 A，且低温融冰电流很大。因此，在极寒天气到来之前，LBGJ-150-40AC地线应尽快启动融冰装置，避免环境温度过低，覆冰厚度增加过快而引起的融冰电流过大或融冰容量过大。

注：覆冰厚度10 mm；风速5 m/s；融冰时间1 h。

2.3 融冰电流与风速的关系

同样，热交换系数h也是关于风速va的函数，于是，计算得到给定条件下，融冰电流与风速的关系如图5所示。

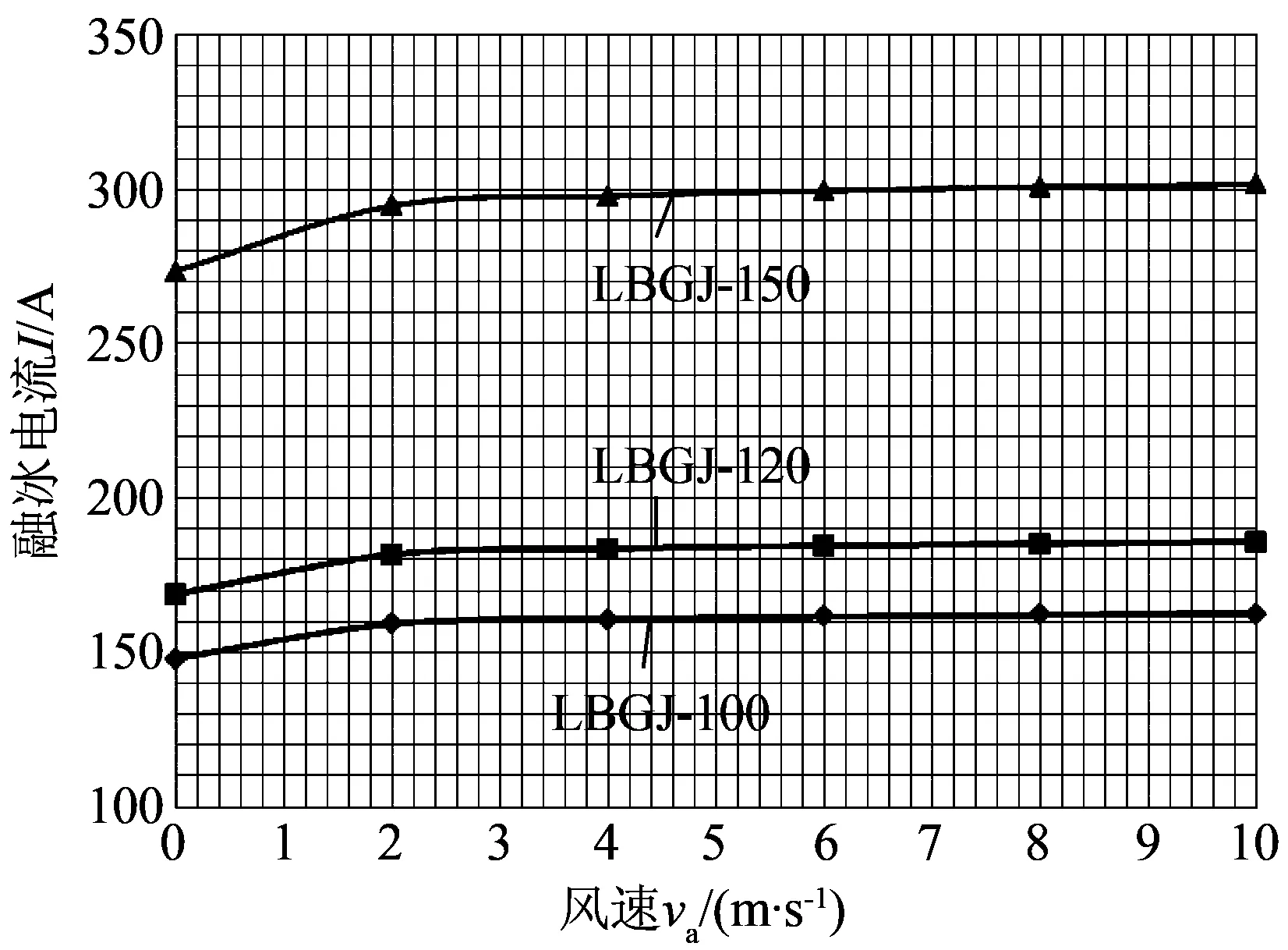
注：环境温度为-5 ℃；覆冰厚度为10 mm；融冰时间为1 h。

由图5可知，风速对融冰电流的影响程度与风速大小有关，其中风速在0～2 m/s，对融冰电流影响较大，风速为2 m/s时，LBGJ-100-20AC和LBGJ-120-20AC地线较无风时融冰电流增加13 A，而LBGJ-150-40AC铝包钢绞线融冰电流较无风时增加约25 A。当风速大于4 m/s时，风速对融冰电流的影响不大。

2.4 融冰电流与融冰时间的关系

根据工程实践经验[17]可得：融冰电流大于临界融冰电流时，融冰时间越短，要求融冰电流越大。本文在给定的融冰条件下，定量地分析融冰时间(0.5～5 h)与融冰电流的关系，见图6。

注：环境温度为-5 ℃；覆冰厚度10 mm；风速5 m/s。

计算结果表明：融冰时间从0.5 h增加到1 h，减少融冰电流十分明显，增加1 h融冰时间，LBGJ-100-20AC、LBGJ-120-20AC铝包钢绞线融冰电流可减少70～82A，融冰时间大于1.5 h后，减少融冰电流趋缓，每增加1 h融冰时间，融冰电流仅减少5～35 A；对于LBGJ-150-40AC铝包钢绞线、融冰时间从0.5 h增加到1 h，增加1 h融冰时间，融冰电流可减少127 A，融冰时间大于1.5 h后，融冰电流变化趋势基本与其他型号地线一致。

2.5 融冰电流与地线材料的关系

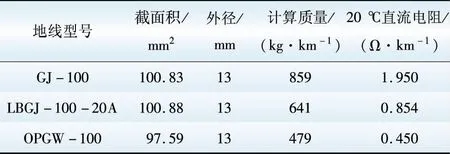
前面以不同型号的铝包钢绞线为例，分析了覆冰厚度di，环境温度Ta，风速va以及融冰时间t对融冰电流的影响，随着地线材料的不同，钢绞线，铝包钢绞线以及光纤复合架空地线对融冰电流的影响也不相同(参数见表2)。根据表2中已知地线参数分别计算LBGJ-100-20A，GJ-100和OPGW-100这3种不同材质，同等尺寸的地线融冰电流，计算得融冰电流与地线材料的关系如图7所示。

计算结果表明：同等融冰时间和气象条件下，地线材料对融冰电流影响很大，钢绞线对融冰电流的要求最小80～140 A，而OPGW对融冰电流的要求最高,达140～300 A。可见，相同气象条件下，地线材料不同，地线融冰电流差异很大，地线直流电阻的大小是影响融冰电流的决定性因素。同尺寸的地线材料，钢绞线因其直流电阻率较大，较铝包钢绞线和OPGW融冰电流小很多。因此地线融冰设计时地线材料参数及气象条件资料的确定是融冰成功与否的关键。

表2 地线基本参数(同等尺寸)

Table 2 Basic parameters of ground wire(same size)

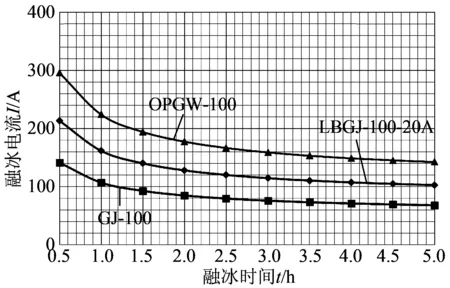
注：环境温度为-5 ℃；覆冰厚度为10 mm；风速为5 m/s。

3 融冰电流的计算

以上分析可得知：融冰时间、气象条件和地线材料等因素对融冰电流的影响较大。本文从工程应用的角度出发，通过本文提出的椭圆融冰模型的融冰电流计算公式(以下简称椭圆公式)计算不同气象条件下、不同型号的铝包钢绞线、OPGW光缆和钢绞线最小融冰电流(地线参数见表3)，并将计算结果和文献[1]中介绍的(在国家电网酒泉—湖南±800 kV特高压直流线路工程、南方电网溪洛渡—广东±500 kV直流线路地线融冰改造及500 kV桂山甲乙线地线融冰改造工程中应用)布尔斯道尔夫融冰电流公式(以下简称布氏公式)计算结果进行对比分析(见表4～6)。

表3 地线基本参数(不同尺寸)

Table 3 Basic parameters of ground wire(different sizes)

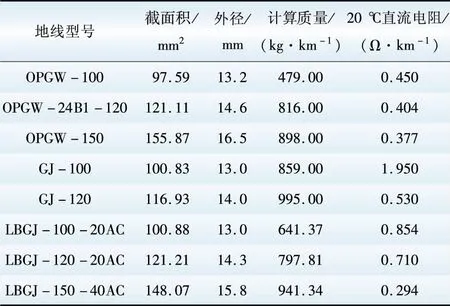
表4 铝包钢绞线融冰电流计算结果

表5 OPGW光缆融冰电流计算结果

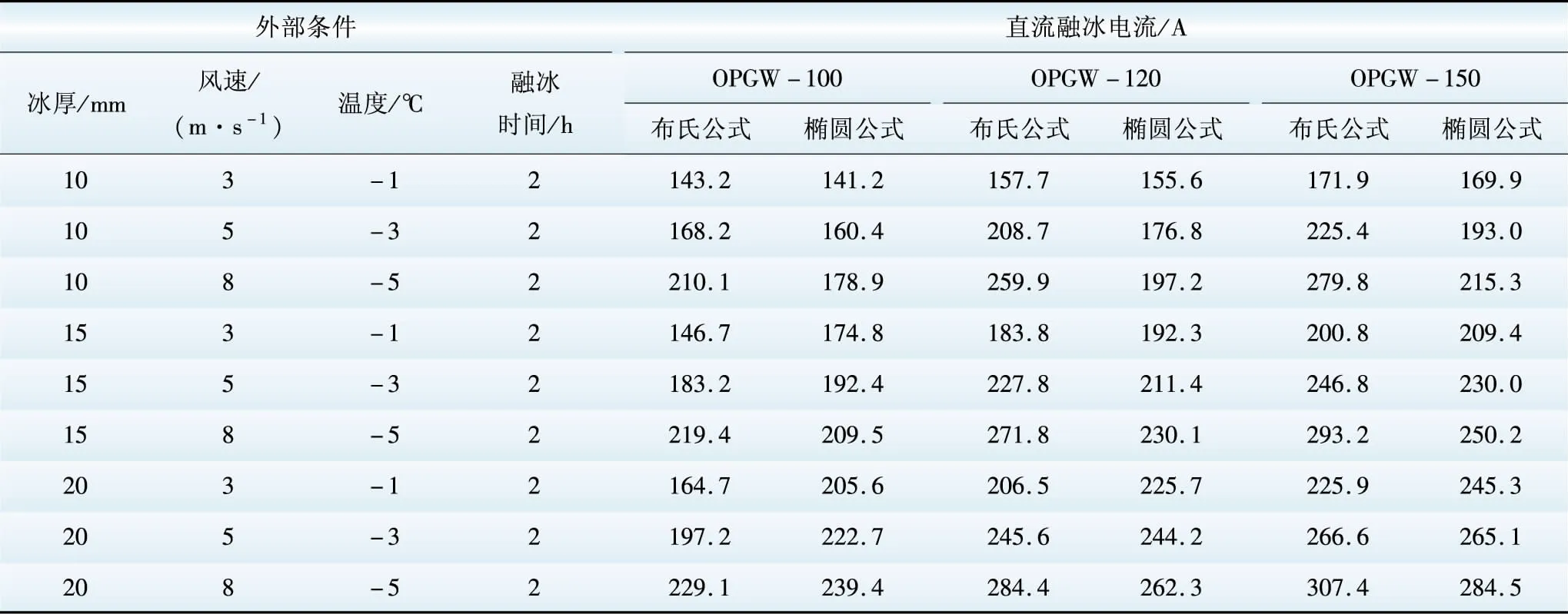
表6 钢绞线融冰电流计算结果

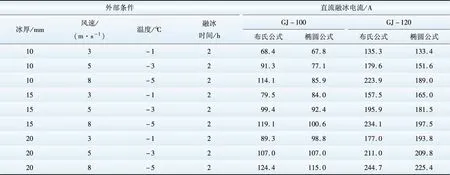
以上数据表明，采用基于椭圆融冰模型的融冰电流公式的计算结果与采用布尔斯道尔夫融冰电流公式的计算结果吻合较好。前者计算结果普遍偏小，但2种计算结果的最大偏差不超过15%。这是由于融冰模型较为复杂，融冰过程中影响因素颇多，每种计算模型的提出都有一定的局限性和误差，比如，椭圆融冰计算模型没有考虑地线温度、气隙等参量的动态变化，因此，输电线路地线融冰需要基于数学计算，结合输电线路运行经验及融冰试验予以确定融冰电流。

4 结 论

本文以工程应用为背景，提出椭圆融冰模型计算输电线路地线融冰时间和融冰电流。首先，通过计算不同规格的铝包钢绞线融冰电流，分析了不同气象条件(风速va、环境温度Ta及覆冰厚度di)、融冰时间t及地线材料对地线融冰的影响。结果表明：环境温度、覆冰厚度及地线材料对地线短路电流融冰均有明显的影响，但风速的影响相对较小，特别在风速大于4 m/s时，风速影响几乎为0；然后，通过椭圆融冰模型计算公式计算几种工程常用的铝包钢绞线、OPGW光缆和钢绞线在不同气象条件下的融冰电流，并将计算结果与在溪洛渡—广东±500 kV直流线路地线融冰改造工程、500 kV桂山甲乙线地线融冰改造工程和酒泉—湖南±800 kV特高压直流线路等工程地线融冰设计中应用的布尔斯道尔夫公式计算结果进行对比。结果表明：2种计算结果基本一致，椭圆融冰模型计算结果相对偏小，但最大偏差不超过15%。实际融冰工程设计中，一般在不超过最大允许电流的前提下，设计最小融冰电流时考虑一定的裕度。因此，椭圆融冰模型同布尔斯道尔夫公式一样适用于地线融冰电流设计，模型简单、计算方便且能更形象直观地解释地线融冰过程。采用本文的椭圆融冰模型可以有效分析架空输电线路地线融冰电流。本文的研究结果为输电线路地线融冰电流的选择及融冰装置的设计提供了有效参考。

[1]赵杰,饶宏,李立浧.电网防冰融冰技术及应用[M].北京：中国电力出版社，2010.

[2]陆佳政, 彭继文, 张红先，等. 2008年湖南电网冰灾气象成因分析[J]. 电力建设, 2009, 30(6): 29-31. Lu Jiazheng, Peng Jiwen, Zhang Hongxian，et al. Icing meteorological genetic analysis of Hunan power grid in 2008[J]. Electric Power Construction, 2009, 30(6): 29-31.

[3]蒋兴良,易辉. 输电线路覆冰及防护[M]. 北京: 中国电力出版社, 2002.

[4]Merrill H M, Feltes J W. Transmission icing: A physical risk with a physical hedge[C]//2006 IEEE Power Engineering Society General Meeting, PES,2006.

[5]PéTER Z. Modeling and simulation of the ice melting process on a current-carrying conductor[D]. Québec: Université Du Québec, 2006.

[6]Huneault M, Langheit C, Caron J. Combined models for glaze ice accretion and de-icing of current-carrying electrical conductors[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1611-1616.

[7]Horwill C, Davidson C C, Granger M. An application of HVDC to the de-icing of transmission lines[C]//2005/2006 IEEE/Pes Transmission & Distribution Conference & Exposition, 2006.

[8]饶宏, 李立浧, 黎小林, 等. 南方电网直流融冰技术研究[J]. 南方电网技术, 2008, 2(2): 7-12. Rao Hong, Li Licheng, Li Xiaolin, et al. Study of DC based De-icing technology in China southern power grid[J]. Southern Power System Technology, 2008, 2(2): 7-12.

[9]蒋兴良,张丽华.输电线路除冰防冰技术综述[J]. 高电压技术,1997, 23(1): 73-76. Jiang Xingliang, Zhang Lihua. De-icing and anti-icing of transmissionlines[J]. High Voltage Engineering,1997, 23(1): 73-76.

[10]杨世铭,陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.

[11]刘和云.架空导线覆冰与脱冰机理研究[D]. 武汉：华中科技大学, 2001. Liu Heyun. Icing and Ice-shedding from conductors on overhead transmission line [D]. Wuhan：Huazhong University of Science and Technology, 2001.

[12]范松海. 输电线路短路电流融冰过程与模型研究[D]. 重庆：重庆大学，2010. Fan Songhai. Study on process and model of ice-melting with short circuit current on iced conductor[D]. Chongqing：Chongqing University，2010.

[13]蒋兴良, 范松海, 胡建林，等. 输电线路直流短路融冰的临界电流分析[J]. 中国电机工程学报, 2009, 30(1): 111-116. Jiang Xingliang，Fan Songhai，Hu Jianlin，et al. Analysis of critical ice-melting current for short-circuit DC transmission line[J]. Proceeding of the CSEE, 2010, 30(1): 111-116.

[14]常浩，石岩，殷威杨，等 交直流线路融冰技术研究[J]. 电网技术，2008，32(5): 1-6. Chang Hao，Shi Yan，Yin Weiyang，et al. Ice-melting technologies for HVAC and HVDC transmission line[J]. Power System Technology, 2008, 32(5): 1-6.

[15]Davidson G A, Donoho T E，Landrieu P R H, et al. Short-time thermal ratings for bare overhead conductors[J]. IEEE Transaction on Power Apparatus and Systems, 1969, PAS-88(3): 194-198.

[16]东北电力设计院.电力工程高压送电线路设计手册[M].北京：中国电力出版社，2003 .

[17]国家电网公司《输电线路融冰技术导则》[M].2010.

(编辑:张媛媛)

Heat Balance Analysis and Calculation of Ground Wire Ice-Melting in Transmission Line

LI Tieding, LI Jian, LYU Jianshuang, HUANG Yucheng

(Central Southern China Electric Power Design Institute, Wuhan 430071, China)

According to the present situation of ice cover of power system in China, combined with the practical experience of ice melting at home and abroad, this paper analyzed the mechanism of ground wire ice melting. On this basis, an elliptic mathematical calculation model was set up for ice-melting, combined with the theory of heat transfer. In the light of the engineering application, the calculation method of minimum ice-melting current was studied. Through the ice-melting current calculation of three kinds of aluminum clad steel wires (LBGJ-100-20AC,LBGJ-120-20AC, LBGJ-150-40AC), this paper analyzed the impact of ice thickness, wind speed, ambient temperature, ice melting time and other factors on ground wire ice-melting; calculated the relationship between different wire materials and ice melting current. Finally, the proposed calculation model was used to calculate the minimum ice-melting current of ground wire materials commonly used in transmission line engineering. Through the comparison of the calculation results with those results of Bauers Dolf ice-melting current calculation formula which was commonly used in transmission line engineering, it shows that two kinds of calculation results are in good agreement. The analysis and calculation results show that the ice-melting current is determined collaboratively by ice thickness, ambient temperature, wind speed and ground wire material; ambient temperature, ice thickness and ground wire material all have obvious influences on the ground wire ice-melting current, but the influence of wind speed is relatively small. The proposed calculation model of ice-melting current can provide useful and valid reference for the selection of ground wires ice-melting current and the design of defroster.

transmission line; ground wire ice melting; heat balance; elliptic ice-melting model; engineering application

Vm=πab-πRc2

b=Rc+di/2

Vi=π(Rc+di)2-πRc2

h=(0.295Ri)-0.534va0.466+4.39×(1+0.01Ta)

中国电力工程顾问集团科技项目(DG1-D03-2013)。

TM 755

A

1000-7229(2015)04-0070-07

10.3969/j.issn.1000-7229.2015.04.012

2014-10-26

2015-01-29

李铁鼎(1987)，男，硕士，工程师，主要从事高压输电线路设计研究工作；

李健(1981)，男，硕士，工程师，从事超高压输电线路及电力电缆工程方面的研究和设计工作；

吕健双(1987)，男，工学硕士，工程师，主要从事高压输电线路设计工作；

黄欲成(1979)，男，高级工程师，主要从事高压输电线路设计研究工作。