配电网中分布式储能系统的优化配置方法

唐文左，梁文举，崔荣，曾锐，贾龙，周川杰，胡泽春

(1.国网重庆市电力公司经济技术研究院，重庆市 401120； 2.清华大学电机系，北京市 100084)

(1. Economic & Technology Research Institute, State Grid Chongqing Electric Power Company, Chongqing 401121, China;2. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China)



配电网中分布式储能系统的优化配置方法

唐文左1，梁文举1，崔荣1，曾锐1，贾龙2，周川杰2，胡泽春2

(1.国网重庆市电力公司经济技术研究院，重庆市 401120； 2.清华大学电机系，北京市 100084)

分布式储能系统接入配电网可与分布式电源形成互补，弥补后者由于出力的随机性对配电网安全和经济运行造成的负面影响，还可对配电网与主网的功率交换进行调节，起到削峰填谷的作用。而对分布式储能系统接入配电网进行优化配置是实现上述作用的基础，基于此，提出了配电网中分布式储能系统的优化配置方法。首先，为处理负荷功率、风电和光伏发电的随机性，利用聚类算法得到典型日负荷曲线、典型风电和光伏发电出力曲线。其次，以储能系统投资与运行成本最小为目标，考虑接入位置、功率大小和配电网安全运行等约束条件，建立多时段非线性混合整数优化模型，并采用两层优化的方法求解模型。该方法在外层采用改进的遗传算法对储能系统的配置方案进行优化，在内层采用最优潮流算法对配置方案的储能充放电进行优化。最后，对一个含风电和光伏发电的配电系统进行测试，证明了该方法的有效性，并分析了风电和光伏发电的额定功率、负荷需求变化等因素对储能系统配置结果的影响。

分布式储能系统；配电网；优化配置；遗传算法；最优潮流算法

0 引 言

随着能源需求的不断增长和环境保护压力的增大，分布式电源的大量并网对电网带来了不容忽视的冲击，电网负荷峰谷差的增大严重影响了电网的安全性和经济性。储能系统的接入为解决这些问题提供了新的途径。储能系统可以有效地实现需求侧管理，消除昼夜峰谷差，平滑负荷，提高电力设备利用率，降低供电成本，提高对新能源发电的消纳能力[1-4]。

目前国内外许多学者对配电网中分布式储能系统的优化配置问题进行了研究。文献[5]通过接入储能系统来延缓变电站的扩容，考虑储能系统的充放电效益来获得购售电价差，并建立了变电站扩容与电池储能系统容量配置的协调规划方案。文献[6]从削峰填谷能力、电压质量以及功率主动调节能力3个方面建立了主动配电网储能系统多目标优化配置模型。文献[7]研究了配电网中引入储能系统在降低发电侧、输配电侧建设容量投资和减少重要用户停电损失费用方面带来的经济价值，分析了降低配电网络损耗和利用分时电价减少电量电费获得的经济效益，建立了经济性最优条件下适合不同储能类型的容量优化配置模型。文献[8]研究了不同分布式电源与储能系统在稳态输出特性下，配置容量和接入位置的优化问题。文献[9]采用了简化的方法来计算配电网运行过程中的网损，根据配电网辐射状的特点建立了电池储能站的优化模型。文献[10]介绍了通过采用遗传算法和序列二次规划(sequence quadratic program, SQP)算法来获取最佳储能设备接入点和接入规模的储能系统优化配置方法，并介绍了4种案例来体现储能系统在智能电网骨架中的潜在优势。文献[11]提出了一种在火力发电系统中接入最佳规模储能系统的方法，并利用禁忌搜索的方法来求解该优化问题。文献[12]介绍了利用Benders分解方法来实现储能系统对电力系统电压控制的最大帮助，并在不同规模、负荷的分布式发电中进行测试。文献[13]提出在含有风电出力的配电网中接入一个电池储能系统，为分布式电源的所有者提供最大的收益，并且确定储能系统的规模来容纳所弃掉的风能，同时分析和验证了电池储能系统的可行性。

分布式储能配置的难点在于充分考虑配电网的不同运行条件(特别是分布式电源的不确定性)和储能系统充/放电的能量耦合约束，但已有文献尚未给出合理的解决方法。基于此，本文对含有分布式电源的配电网中接入储能系统的最优配置问题进行研究。采用聚类算法得到负荷和出力的典型日曲线，用于系统运行条件的评估和选取。以投资和运行成本最小为目标，考虑储能系统接入位置、功率/能量和配电网安全运行约束等条件，建立多时段混合整数非线性优化模型。利用遗传算法在外层对储能系统的容量和位置进行优化，在内层通过多时段最优潮流计算来评估每种方案的适应度函数，最终得到最佳的储能系统配置方案。

1 典型日的确定方法

在规划期内对储能系统在配电网中的运行状况进行模拟评估，需要对负荷需求的变化以及配电网中分布式电源的出力变化进行分析，这两者的变化对储能系统的成本评估至关重要。

本文考虑风电和光伏发电两类分布式电源。对负荷、风电和光伏发电按年度考虑其变化特性。同时，考虑到1年内负荷和分布式发电的数据量很大，本文采用多个典型日来代表全年负荷、风电和光伏发电的变化。这样不仅可以较好地反映负荷和分布式电源的变化，有利于客观地评估储能系统的配置方案，而且还可以大大提高计算的效率。采用聚类的方法处理历史数据，从而得到负荷、风电和光伏发电的典型日曲线。

1.1k均值聚类算法

k均值聚类算法计算简单、收敛速度较快，因此本文采用该算法进行聚类分析。其聚类原则为最小化样本与所属聚类中心的距离，如式(1)所示。

(1)

式中：a为初始聚类中心个数；N为样本数；n为样本编号；cnm为第n个样本是否属于m类;xn为待聚类的相关因素;ωm为类Rm的聚类中心。

cnm定义如下：

(2)

1.2 聚类中心的确定

k均值算法对聚类中心初始点的要求较高，可能会因初始点的不同而导致最终结果的不同，因此需要合理地选择聚类中心。基本的解决方法如下：

(1)确定聚类的数目m；

(2)将样本从小到大排列；

(3)将样本平均分成m个区间，确定每个区间的样本数，对样本从小到大排序并进行区间划分；

(4)计算每个区间的样本平均值，平均值即为该区间的初始聚类中心。

按照以上聚类算法的步骤，从不同的划分角度可以得到负荷、风电和光伏发电等多个典型日曲线，同时考虑三者之间的相关性进行相互分组，可以得到多个场景下的典型日曲线组合，每个场景在1年中对应有不同的天数。

2 分布式储能系统优化配置模型

本文对含有分布式电源的配电网中配置储能系统的接入位置和接入容量进行优化研究，并对每种配置方案进行经济性评估，从而确定最优的储能系统配置方案。

2.1 目标函数

考虑配电网的网损费用、储能系统投资成本、主网和分布式电源向配电网注入无功功率的费用，以及储能系统通过价格套利的收益，目标函数如式(3)所示。在成本和收益计算时，考虑投资储能系统的运行年限，在1年内分析多个典型日，并计算规划期内资金的时间价值，统一将所有费用折算成现值。

F=CLOSS+CQ,HV+CQ,DG+CPA+CDESS

(3)

式中：CLOSS为网损费用；CQ,HV为从高压网侧吸收无功功率的费用；CQ,DG为分布式电源提供无功功率的费用；CPA为价格套利所实现的收益；CDESS为安装储能系统的投资费用。

(4)

式中：Nt为不同典型日的种类个数；Ndays,m为每种典型日所对应的天数；NY为规划周期年数;a为贴现率；PrL,y,k为第y年第k个时段的单位网损费用，元/(MW·h)；αL为考虑通货膨胀情况下PrL,y,k每年的增长率；NL,y为不同负荷水平下的时间间隔数量；PL,y,k为第y年第k个时段的网损值， MW；ΔTy,k为第y年第k个时段的时间长度，h。

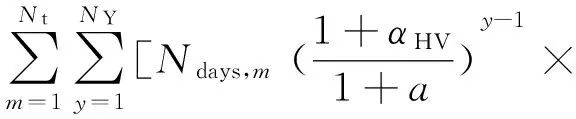
(5)

式中:PrHV,y,k为第y年第k个时段的高压网侧注入无功功率的单位费用，元/(Mvar·h)；αHV为考虑通货膨胀情况下PrHV,y,k每年的增长率；QHV,y,k为第y年第k个时段高压网侧注入无功功率值，Mvar。

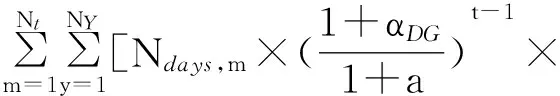
(6)

式中:PrDG,y,k为第y年第k个时段分布式电源提供无功功率的单位费用，元/(Mvar·h)；αDG为考虑通货膨胀情况下PrDG,y,k每年的增长率；QDG,y,k为第y年第k个时段分布式电源提供的无功功率值，Mvar。

(7)

式中:PrEn,y,k为第y年第k个时段有功能量的单位费用，元/( MW·h)；αDESS为考虑通货膨胀情况下PrEn,y,k每年的增长率；PDESS,y,k为第y年第k个时段所有分布式储能系统总的有功功率值， MW。

(8)

2.2 约束条件

考虑的约束条件主要包括配电网节点功率平衡约束、分布式发电电源的出力约束、节点电压幅值约束、支路有功功率约束、储能系统电量平衡约束、荷电状态约束、储能系统功率及充放电功率约束和储能系统的数量约束。

(1)节点功率平衡约束：

(9)

(10)

式中：Pit、Qit分别为t时段节点i的注入有功和无功功率(为负荷、发电出力、储能功率的净功率)；Uit、Ujt分别为t时段节点i、j的电压；δit、δit分别为t时段节点i、j的相角；Gij、Bij分别为节点导纳矩阵第i行第j列的实部、虚部；N为节点总数。

(2)发电机出力约束：

(11)

(3)节点电压约束：

(12)

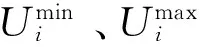
(4)支路有功约束：

(13)

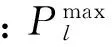
(5)储能系统电量平衡约束：

(14)

式中：SOCx,0、SOCx,t分别为储能系统x初始时刻和t时刻的荷电状态；ηC,x、ηD,x分别为储能系统x的充电和放电效率；PC,x、PD,x分别为储能系统x的充电功率和放电功率；ES,x为储能系统x的额定容量。

(6)荷电状态约束：

(15)

(7)储能系统功率约束：

(16)

式中：PDESS,i,t为节点i处储能系统在t时段的实际充/放电功率；PC,i,t、PD,i,t分别为t时段的充电和放电功率。

(17)

(8)储能系统充放电功率约束：

(18)

(19)

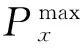
(9)储能系统数量约束：

(20)

(21)

式中：nDESS为配电网中接入储能系统的实际个数；nmax为允许接入储能系统个数的上限。

3 模型求解方法

3.1 求解流程

第2节所建立的分布式储能系统优化配置模型是一个非线性混合整数优化问题。本文采用改进的遗传算法对储能系统的配置方案进行优化，在遗传算法的内部运用MATPOWER[14]中的最优潮流算法对各种储能系统的配置方案进行评估，通过目标函数的比较，筛选出较优的配置方案，并保留到下一代，通过外层的遗传算法不断优化，对配置方案进行评估，直至满足收敛条件，得出最优的分布式储能系统配置方案。具体算法的实现流程如图1所示。

输入的数据包括目标函数、网络约束条件、储能系统接入位置及功率约束条件相关的参数，典型日数据及所对应的天数，网损单位价格，储能系统安装单位价格，高压网侧注入无功功率的单位价格，分布式电源提供无功功率的单位价格，有功能量单位价格，以及通货膨胀所引起的价格增长率，贴现率，规划周期，遗传算法种群的个数、最大遗传代数。

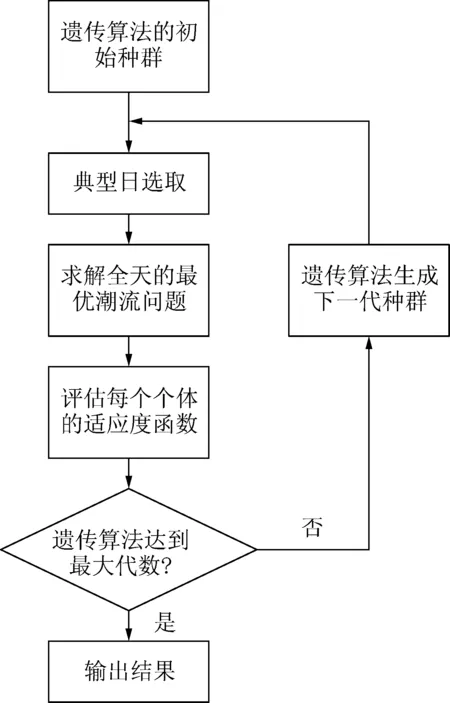
图1 算法实现流程图

输出的结果包括最佳分布式储能系统配置方案的接入节点及功率，最佳配置方案在规划周期内所需的总费用，以及在遗传迭代过程中，每一代种群中最佳配置方案的适应度函数值等。

3.2 遗传算法

遗传算法需要建立一个初始种群，种群中的每个个体用一串二进制数来编码，每个个体分别代表一种优化配置方案，即储能系统接入的节点及功率。

对于每个个体，先选择一种典型日，确定风电、光伏发电出力及负荷需求之后，通过内部最优潮流的计算，得到有功功率、无功功率等数据，然后计算得到目标函数。每种方案的目标函数在遗传算法内部即为该方案的适应度函数的相反数，对于种群中的每个个体，适应度函数可以分别对其进行评价，若一个个体的目标函数值越小，则适应度函数值就越大，适应度越高，被保留到下一代的概率就会越大，式(22)为适应度函数的表达式：

(22)

根据适应度函数可以筛选出优质的个体保留到下一代，直至找到最优解。遗传算法主要通过选择算子、交叉算子和变异算子来对个体进行优化。

3.3 最优潮流

内层问题是一个多时段的最优潮流模型，模型中的储能系统的电量平衡约束(14)与多个时段关联。本文在MATPOWER中最优潮流算法的基础上，进行多时段约束的扩展并加入储能系统的功率和能量耦合约束，实现了内层模型的可靠求解。

4 算例分析

4.1 参数设置

本文选取的测试系统为一个含有17个节点的配电系统[10]，如图2所示。该系统中节点1属于高压电网，通过一台138/12.5kV，18MVA的变压器与配电网馈线相连。光伏发电单元分别接入节点6、13、17，每点接入的功率为1MW，节点9有一台1MW的风力发电机接入。

图2 测试网络结构拓扑图

接入分布式储能系统的待选节点为2号至17号节点，且最多只能在2个节点同时接入储能系统。选取化学电池作为储能系统，储能单元的额定功率可选0.25，0.5，0.7，1.0 MW，每个节点允许接入储能系统的最大功率为1 MW。TDESS,s取整数，范围为[1,8]h。

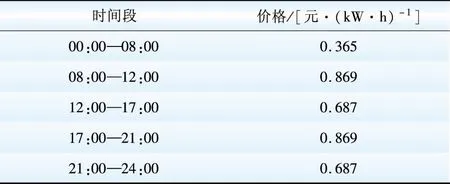
选取我国某地区电能价格表，每日的电能价格随时间段变化如表1所示[15]。假设电价(包括有功功率和无功功率价格)逐年增长率为2%，贴现率为5%。

表1 电能价格表

Table 1 Electricity price

4.2 典型日组合

首先通过聚类方法，分别得到负荷、风电和光伏发电的3种典型日曲线，如图3～5所示。

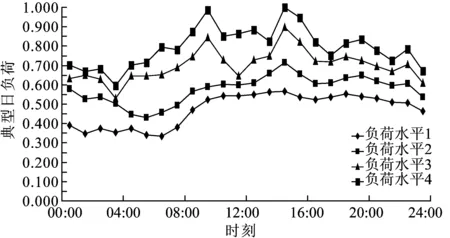
图3 负荷典型日曲线

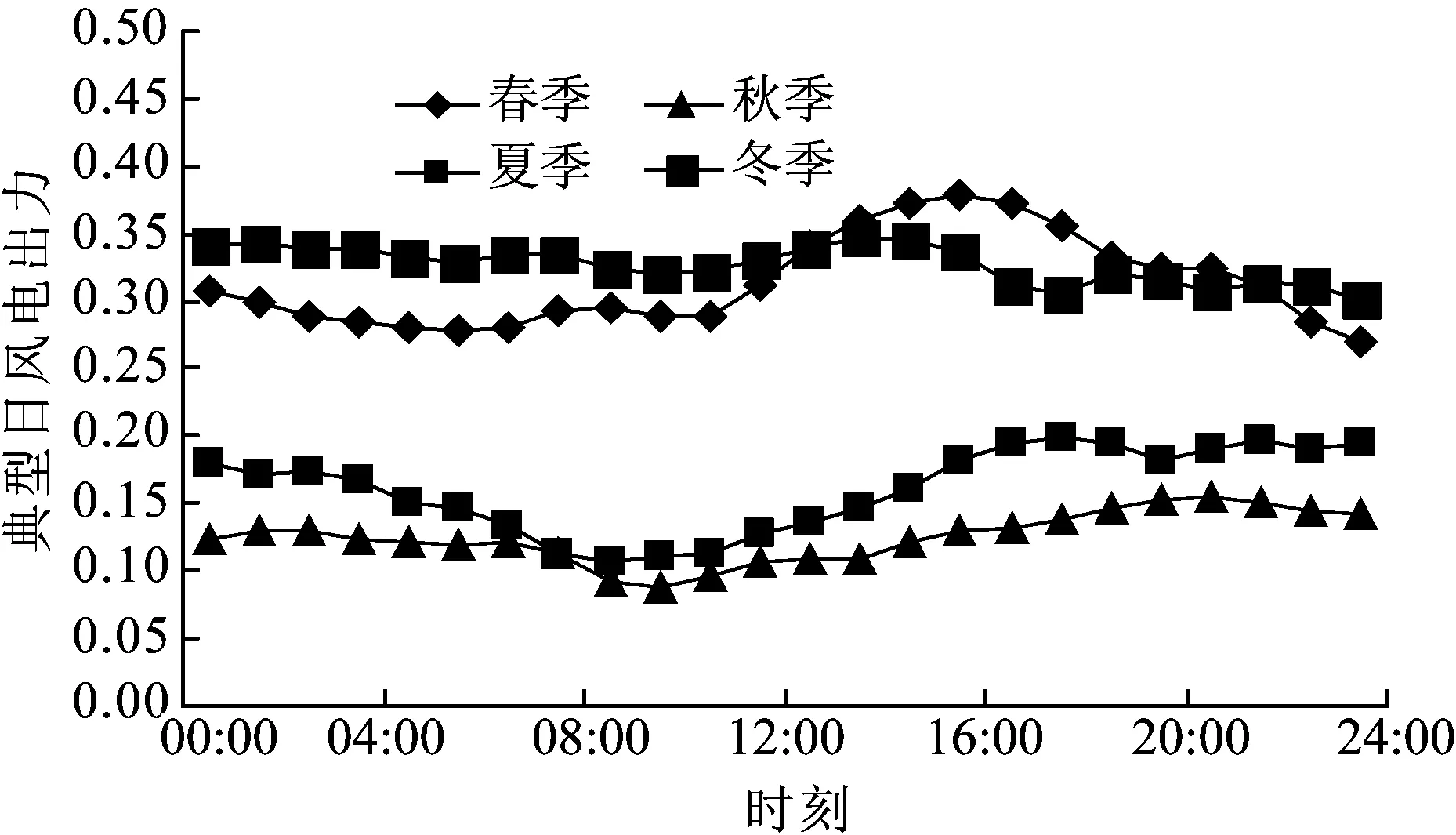
图4 风电典型日曲线

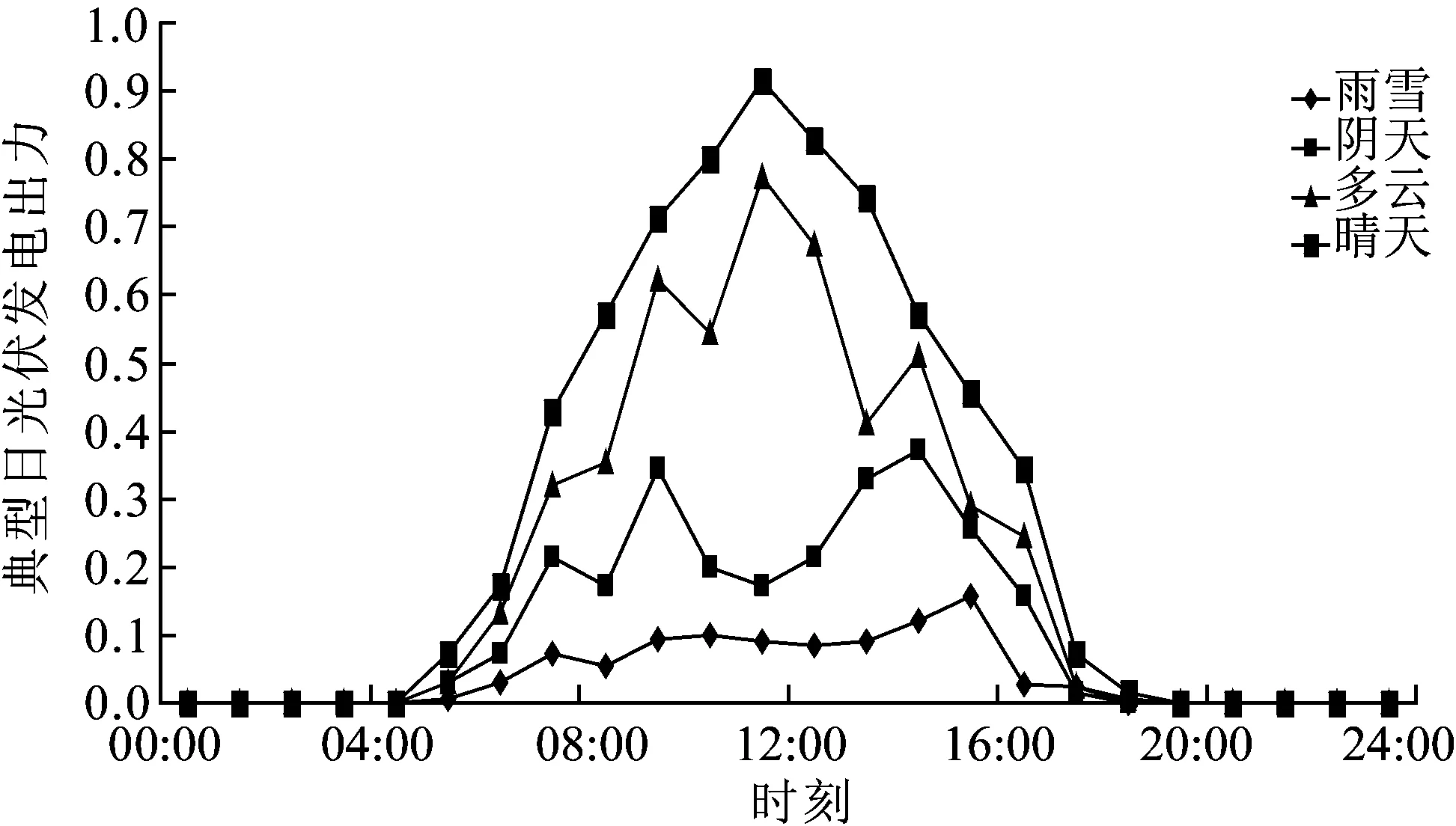
图5 光伏发电典型日曲线

在储能系统的评估体系中，综合考虑各种典型日曲线的相关性，进行负荷、风电和光伏发电典型日曲线的整合，即考虑在不同场景下储能系统在配电网中的运行情况，对各种场景下的目标函数进行求解，从而得到总的目标函数值。考虑天气和季节的变化因素，共采用16种组合的典型日曲线，其组合方式及对应天数如表2所示。

表2 组合典型日的天数

Table 2 Days of combination of typical days

4.3 优化结果

依次选择16种典型日曲线组合进行最优潮流计算，根据潮流计算结果求解目标函数，进行方案评估，最大遗传迭代次数为100代，遗传算法的交叉率为0.7，变异率为0.05。通过程序运行获得最佳的分布式储能系统配置方案：节点2、6接入功率都为1.0 MW的储能系统，持续时间为1 h，总成本为2 608.82万元。

分析迭代过程中每代种群最佳配置方案目标函数的变化情况发现，最佳方案目标函数值总体上有减小的趋势，但减小的次数偏少，遗传算法的效率较低，且有过早收敛的趋势，因此需要对遗传算法进行改进。

4.4 遗传算法改进

首先，改进遗传算法种群的保留方式，每次将上一代最优的个体保留至下一代，保证最优个体的延续，再将剩余的n-1个个体进行2次交叉变异后，进行最优潮流计算，求出目标函数值并进行升序排列，取出奇数位的个体(其中包含交叉变异后最优的个体)作为下一代的个体，这样使得种群具有多样性的特点，能在全局进行充分寻优，防止陷入局部优化。

其次，在建立初始种群时即生成配置方案的记录表，以防止在迭代过程中重复计算前面已计算过的配置方案，若一种配置方案没有在记录表中记录过，则会针对这个方案进行最优潮流的计算并记录在表中，若在迭代过程中再一次出现曾经计算过的配置方案，则可以直接从记录表中提取出目标函数值。这样可以提高程序的运行效率，实际计算表明，运行时间缩短到原来的40%左右。

此外，对遗传算法中交叉率和变异率进行了修改，选取交叉率和变异率的最优组合，通过文献调研和反复测试，本文将交叉率设定为0.9，变异率设定为0.004。应用改进的遗传算法可以得到明显的种群进化趋势，且没有过早收敛进入局部极小值，明显提高了遗传算法对于种群进化的效率，便于找到全局的最优解。改进后的最佳配置方案：节点5、6接入功率都为1.0 MW的储能系统，持续时间为1 h，总成本为2 541.98万元。

4.5 灵敏度分析

(1)风电额定功率。

考虑风电装机容量的不确定性，对风电机组的额定功率进行灵敏度分析。表3列出了不同的风电额定功率对储能最优配置方案及成本的影响。

表3 不同风电功率下的储能配置结果

Table 3 Results of energy storage allocation under different wind power

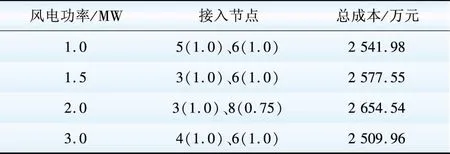
注：“()”中为对应节点接入储能系统的功率， MW；储能持续时间都为1 h。

由表3可知，风电额定功率的增大对储能系统配置的影响不大，总成本基本保持不变，储能功率和容量基本保持不变，接入点有一定的变化。

(2)光伏发电额定功率。

同样，对光伏发电单元的额定功率进行灵敏度分析。表4列出了不同的光伏发电额定功率对储能最优配置方案及成本的影响。

表4 不同光伏发电功率下的储能配置结果

Table 4 Results of energy storage allocation under different photovoltaic power

注：储能系统的功率为1.0 MW，持续时间为1 h。

由表4可知，光伏额定功率的增大同样对总成本的费用影响不大。储能系统的容量和功率都没有变化，对接入的节点有一定的影响。需要说明的是，表3和表4的结果是在风电和光伏发电接入基本不影响配电网安全运行的条件下得出的结论。如果风电或光伏发电的接入引起设备过载或电压越限，则储能配置的结果可能发生较大的变化。

(3)负荷需求。

进一步，对配电网负荷需求进行灵敏度分析，原配电网负荷需求的总功率为11.6 MW。表5列出了不同的负荷需求总功率对储能最优配置方案及成本的影响。

表5 负荷需求灵敏度分析结果

Table 5 Results of load demand sensitivity analysis

注：“()”中为对应节点接入储能系统的功率，MW。

由表5可知，当负荷需求增大之后，总成本显著增加，储能系统在节点中的分布发生变化，对于接入的储能的容量需求增大。

(4)储能单位容量成本。

表6 不同储能单位成本下的储能配置结果

Table 6 Results of energy storage allocation under different unit costs

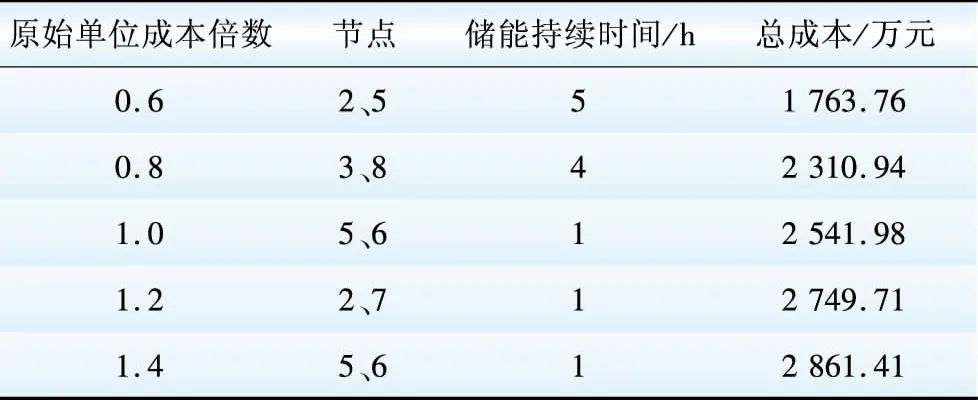
注：接入储能系统的功率都为1.0 MW。

由表6可知，当储能系统的单位成本降低时，接入的储能容量显著增大，总成本也显著降低；当储能系统的单位成本增加时，接入的储能容量降低，总成本则显著升高。

5 结 论

(1) 以典型日为分析单元，采用聚类分析的方法，同时考虑配电网中负荷、分布式风电和光伏出力变化的影响，可获得用于分布式储能规划的配电网典型运行场景。

(2) 以配电网的运行费用和储能系统的投资成本最小为目标，建立了多时段混合整数非线性优化模型，较全面地考虑了储能系统充电放电约束、电量平衡约束和价格套利收益。

(3) 采用遗传算法对所建模型进行求解，提高了算法的收敛性和全局寻优能力；通过求解多时段最优潮流评估每种个体的适应度，可有效处理配电网全天运行状态的变化和储能系统的能量耦合约束。

(4) 算例分析结果表明，所提出的分布式储能系统优化配置模型和方法可以得到较合理的配置方案，能够为储能系统的投资提供科学的决策支持。

进一步的研究将深入考虑日负荷功率和分布式电源出力的相关性，并更为精细地考虑储能系统的成本、功率和电量间隔。

[1]王承民, 孙伟卿, 衣涛, 等. 智能电网中储能技术应用规划及其效益评估方法综述[J]. 中国电机工程学报, 2013, 33(7): 33-41. Wang Chengmin, Sun Weiqing, Yi Tao, et al. Review on energy storage application planning and benefit evaluation methods in smart grid[J]. Proceedings of the CSEE, 2013, 33(7):33-41.

[2]董力通, 徐隽,刘海波.DSM与储能技术在峰值负荷管理的应用及效果[J].中国电力,2012,45(4):47-50. DONG Li-tong , XU Jun , LIU Hai-bo.Application and analysis of DSM and energy storage technology for industrial peak load management[J].Electric Power,2012,45(4):47-50.

[3]金一丁,宋强, 陈晋辉,等.大容量电池储能电网接入系统[J].中国电力,2010,43(2):16-20. JIN Yi-ding,SONG Qiang,CHEN Jin-hui, et al.Power conversion system of large scaled battery energy storage[J].Electric Power,2010,43(2):16-20.

[4]周雪松,权博, 马幼捷,等.超导磁储能装置在风电系统控制中的应用[J].中国电力,2010,43(6):6-9. ZHOU Xue-song,QUAN Bo,MA You-jie, et al.Applications of a super-conducting magnetic energy storage system in a wind power system[J].Electric Power,2010,43(6):6-9.

[5]李振文, 颜伟, 刘伟良, 等. 变电站扩容和电池储能系统容量配置的协调规划方法[J]. 电力系统保护与控制, 2013, 41(15): 89-96. Li Zhenwen, Yan Wei, Liu Weiliang, et al. Coordinated planning of substation expansion and BESS sizing[J]. Power System Protection and Control, 2013, 41(15):89-96.

[6]尤毅, 刘东, 钟清, 等. 主动配电网储能系统的多目标优化配置[J]. 电力系统自动化, 2014, 38(18): 46-52. You Yi, Liu Dong, Zhong Qing, et al. Multi-objective optimal placement of energy storage systems in an active distribution network[J]. Automation of Electric Power System, 2014, 38(18):46-52.

[7]胡荣, 任锐焕, 杨帆, 等. 配电网中储能系统优化配置研究[J] 华东电力, 2014, 42(2): 345-349. Hu Rong, Ren Ruihuan, Yang Fan, et al. Optimal allocation of energy storage system in distribution network[J]. East China Electric Power, 2014, 42(2):345-349.

[8]吴文宣. 不同类型分布式电源在配电网中的优化布置[J]. 现代电力, 2012, 29(3): 6-11. Wu Wenxuan. The optimal placement of different types of distributed generation in distribution network[J]. Modern Electric Power, 2012, 29(3):6-11.

[9]章美丹, 宋晓喆, 辛焕海, 等. 计及网损的配电网电池储能站优化运行策略[J]. 电网技术, 2013, 37(8): 2123-2128. Zhang Meidan, Song Xiaozhe, Xin Huanhai, et al. Optimal operation strategy of battery energy storage system in distribution networks with consideration of power losses[J]. Power System Technology, 2013, 37(8): 2123-2128.

[10]Carpinelli G, Celli G, Mocci S, et al. Optimal integration of distributed energy storage devices in smart grids [J]. IEEE Transactions on Smart Grid, 2013, 4(2):985-995.

[11]Chakraborty S, Senjyu T, Toyama H, et al. Determination methodology for optimising the energy storage size for power system [J]. IET Generation, Transmission & Distribution, 2009, 3(11):987-999.

[12]Nick M, Hohmann M, Cherkaoui R, et al. On the optimal placement of distributed storage systems for voltage control in active distribution networks[C]//Innovative Smart Grid Technologies (ISGT Europe), 2012 3rd IEEE PES International Conference and Exhibition on, IEEE, 2012: 1-6.

[13]Atwa Y M, El-Saadany E F. Optimal allocation of ESS in distribution systems with a high penetration of wind energy [J]. IEEE Transactions on Power Systems, 2010, 25(4): 1815-1822.

[14]Zimmerman R D, Murillo-Sánchez C E, Thomas R J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education[J]. IEEE Transactions on Power Systems, 2011, 26(1):12-19.

[15]徐智威, 胡泽春, 宋永华, 等. 充电站内电动汽车有序充电策略[J]. 电力系统自动化, 2012, 36(11): 38-43. Xu Zhiwei, Hu Zechun, Song Yonghua, et al. Coordinated charging of plug in electric vehicles in charging stations[J]. Automation of Electric Power Systems, 2012, 36(11):38-43.

[16]金虹, 衣进. 当前储能市场和储能经济性分析[J]. 储能科学与技术, 2012, 1(2):103-111. Jin Hong, Yi Jin. Market and economic analysis of the energy storage industry[J]. Energy Storage Science and Technology, 2012, 1(2):103-111.

(编辑:张小飞)

Optimal Allocation Method of Distributed Energy Storage System in Distribution Network

TANG Wenzuo1, LIANG Wenju1, CUI Rong1, ZENG Rui1,JIA Long2, ZHOU Chuanjie2, HU Zechun2

When connected into the distribution network, distributed energy storage system (DESS) can be coordinated with distributed generations (DGs), make up for the negative effects on network safety and economic operation because of DGs’ random outputs, and regulate the power exchange between distribution and main network for peak load shifting. The optimal allocation of DESS connected in distribution network is the basis to bring all these benefits. Therefore, this paper proposed the optimal allocation method for DESS in distribution network. Firstly, the load curve, wind power curve and photovoltaic power curve of typical days were obtained with clustering algorithm to consider the randomness of all the three curves. Secondly, considering the constraints of location, power and the safe operation of distribution network, the multi-period mixed-integer nonlinear optimization model was established with the objective of minimum total investment and operation cost of DESS. Then a two-level optimization method was proposed to solve the model, which used improved genetic algorithm to optimize the DESS allocation scheme at outer layer and optimal power flow algorithm to optimize energy storage charging/discharging of the allocation scheme at inner layer. Finally, a distribution system with wind and photovoltaic power was tested to prove the effectiveness of the proposed method; and the impact of wind and photovoltaic power rating, load demand changes and other factors on the allocation results of DESS were analyzed.

distributed energy storage system; distribution network; optimal allocation; genetic algorithm; optimal power flow algorithm

PDESS,i,t=xi(PD,i,t-PC,i,t)

nDESS≤nmax

FGA=-F=-(CLOSS+CQ,HV+CQ,DG+CPA+CDESS)

(1. Economic & Technology Research Institute, State Grid Chongqing Electric Power Company, Chongqing 401121, China;2. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China)

TM 72

A

1000-7229(2015)04-0038-08

10.3969/j.issn.1000-7229.2015.04.007

2015-01-05

2015-02-05

唐文左(1982)，男，本科，工程师，主要从事电力系统分析与电网规划方面的工作；

梁文举(1983)，男，硕士，工程师，主要从事电网规划及电气计算校核分析方面的工作；

崔荣(1964)，男，高级工程师，主要从事工程造价与电网规划工作；

曾锐(1984)，男，工程师，主要从事配网规划工作；

贾龙(1988)，男，博士研究生，主要从事电动汽车、电力系统优化规划相关的工作；

周川杰(1992)，男，本科，主要从事储能系统优化配置工作；

胡泽春(1979)，男，博士，副教授，主要从事智能电网、电力系统优化规划与运行相关的工作。