基于混沌分析法的舰船电力系统稳定性研究

马洪涛

(江苏海事职业技术学院，江苏 南京 211170)

基于混沌分析法的舰船电力系统稳定性研究

马洪涛

(江苏海事职业技术学院，江苏 南京 211170)

摘要：对舰船电力系统进行分析建模，并根据电力系统模型状态的非线性混沌特征，结合模型幅值扰动参数，分析出混沌现象产生的原因和影响因素。在此基础上，有针对性地利用自适应反演算法在模型中引入适当的控制器，有效地避免电力系统运行中因干扰进入混沌震荡状态，保证了舰船电力系统的正常运行和舰船的安全稳定。研究结果表明，即使舰船电力系统出现混沌现象时，也可以根据其特征状态进行有效的稳定性控制，保持舰船的综合性能。

关键词：混沌分析；电力系统；稳定性

0引言

舰船吨位的增加和舰船结构设计的复杂给舰船设备制造提出了更高要求。随着电力电子技术、信息技术、计算机技术的广泛应用，大量的舰船设备中都嵌入了这些新技术以完善综合控制系统的智能型和灵敏性。在舰船控制系统中，尤其是电力系统扮演着舰船生命力的角色，成为舰船综合性能评价的关键[1-2]，因此，对舰船电力系统的研究也随着认识程度不断深入。在舰船动力系统中，因电力电子器件的物理特性会造成电力系统工作的非线性震荡现象产生，这些现象在一定程度上影响着舰船性能的稳定。而非线性中的混沌现象由于其无规则、无周期、无目的性给舰船的运行带来威胁。因此对舰船电力系统的混沌现象进行研究，最大限度地进行预防控制，保持系统的整体稳定，有着极为重要的价值和意义。考虑到舰船电力系统的混沌现象与陆地的电网电力结构不同，具有环境湿度大、空间容量小和电子器件集成度高的特点，本文选择在电力系统具体工作的数学模型基础上，动态性地对其工作中的混沌扰动现象进行针对性研究，为舰船电力系统的稳定运行、避免混沌现象的出现提供有价值的研究成果和经验借鉴。

1电力系统装置

1.1　电力装置设备

舰船电力系统在正常条件下，主要依靠内部的电网系统向各个电力装备供电，系统主要由供电装置、传输装置和负载组成，按照一定的结构方式形成一个系统整体，以提供给舰船各个用电设备使用。舰船的用电设备按照不同的设备类型可分为机械电力设备、照明电力设备、远洋防卫设备及生活用电设备等。这些设备需要统一的供电系统的运行以保证正常的供应，无论在什么情况下，电力系统的故障都是对舰船性能的损害，所以，电力系统的稳定对舰船的使用和性能状态的作用很大，对舰船电力系统的稳定性研究意义重大[3]。

1.2　系统的混沌现象

研究人员从电力系统的分析中发现，在电力系统运行过程中，因电子器件非线性的震荡造成了系统的无规则性，进而引发混沌震荡，需要采取措施和方法避免该震荡发生。随着舰船结构的复杂和武器装备控制的精密，发电机组也不断增多以维持足够的能量，电力系统的稳定性日益重要。一旦电力系统的供应出现混沌震荡的偏差，对舰船的性能有致命影响，所以需要根据电力系统运行的状态参数进行分析，以避免混沌震荡的现象出现，从机理上消除电力系统的非线性混沌现象，保障舰船电力系统的稳定性。

2舰船电力系统数学模型

2.1　发电机数学模型的建立

舰船电力系统在运行时，因系统电子器件的特性不可避免的出现非线性混沌状态，然而这种状态并非无法解决，随着计算机技术的发展和现代化的系统性仿真软件的出现，可以通过对舰船电力系统建立相应的数学模型进行技术分析，为舰船电力系统中出现的混沌现象的发生机理分析提供了可能。其结构组成如图1所示。

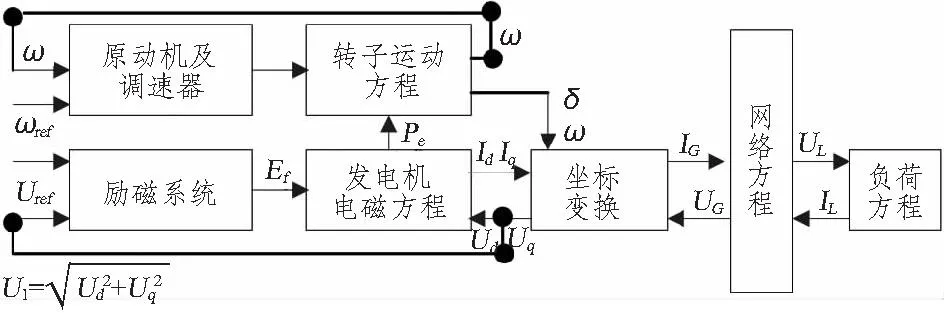
图1　系统结构图Fig.1　System structure diagram

通过对图1中各环节进行建模，对电力系统的运行特征、功率状态等进行推导就可以定量地进行模型分析，在建立数学模型时，将上述结构简化为电机系统的磁导率为恒值，电机的转子对称，且电机的定子绕组空间位置在方向是为互相120°，电机通风器不影响电机工作产生的电感，同时为了方便进一步的优化，系统设置2组电机系统，则图1磁链结构方程如下：

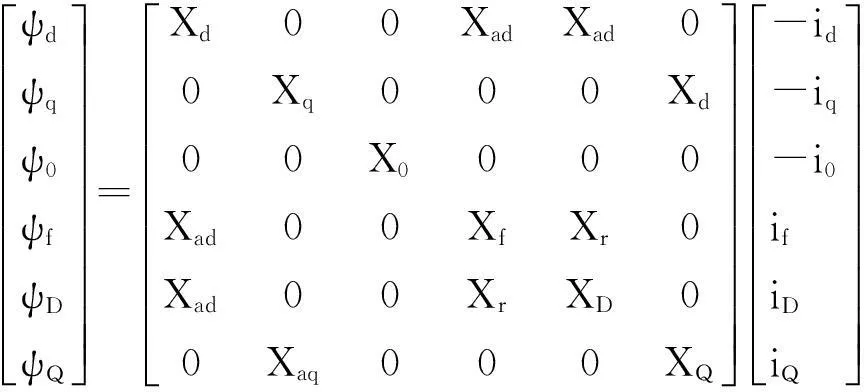
电压表示如下：

则基值为：

转化得到的定子和转子电压方程分别为：

在上述方程的基础上，电磁转矩方程如下：

Te=ψdiq-ψqid，

则转子方程为:

其中功角δ和功角速度ω的关系如下：

该公式即为电力系统运行的各环节数学模型。

2.2　混沌现象分析

舰船电力系统随着舰船综合性能的提高而逐渐复杂[4]。因此，对舰船电力系统中的低频振荡与混沌震荡等非线性现象进行研究具有非常重要的实际意义。混沌现象在电力系统中的出现，具有无周期和不规则性[5]。在系统运行稳定时也有可能发生，对舰船的稳定性造成极大的危害。当系统运行中任何干扰因素且存在阻尼现象，系统的状态为：

上式中设置在某时刻的初始条件，对该系统状态的分析可以引入雅克比矩阵：

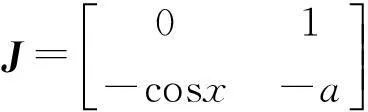
上式可根据参数的值求出系统的稳定点，如在时刻t时，参数C取值在[-4,4]区间，分别取x(1)=(arcsinc,0),x(2)=(π-arcsinc,0)。 在系统受到扰动时，稳定点在混沌分析中称作吸引子，参数C在区间的变化相图如图2所示。

图2　C变化相图Fig.2　C phase diagram of the change

从图2可看出，系统在吸引子附近及偏离吸引子的区域的特征有着明显的不同，当系统取初始值(0.4,0.2)，且参数c=0.2时的时域图曲线如图3所示。

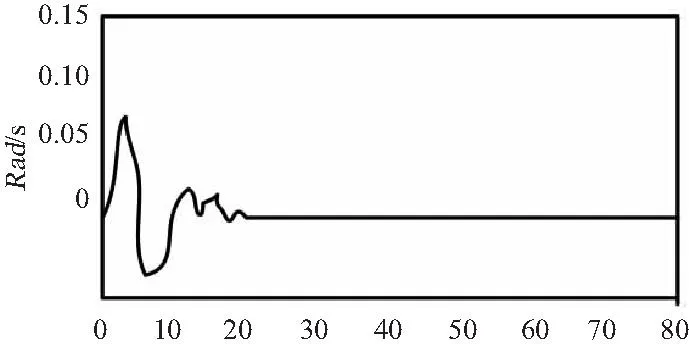
图3　系统时域图Fig.3　Time domain chart of system

由图3可知，当系统在初始条件下，系统运行出现非线性混沌性震荡时，由于吸引子因素的存在，系统会通过自身的调节以重新回归正常，而保持正常的方法便是在模型状态中设置合理的参数值，参数值确定可以根据雅克比矩阵的特征方程值来计算。因此在电力系统数学模型中，分析混沌现象并保证系统的稳定就需要选取合适的稳定点作为吸引子进行判据分析，当系统模型中选取的初始值在吸引子附近时便可保证电力系统运行处于收敛稳定的状态。

3基于混沌分析的舰船电力系统稳定性研究

3.1　舰船电力系统的非线性模型

当对电力系统模型进行分析时，需要转移到舰船电力系统是一个封闭的与外界不联系的系统[6]。其运行的非线性特征可以非线性模型为基础分析，舰船电力系统都是多机组同时维持舰船电力的供应，为简化模型分析，现以2台发电机组进行模型状态分析(见图4)。

图4　发电机模型Fig.4　Generator model

图中：E1∠δ1，E2∠δ2为电压，Xd1和Xd2为电抗，R为电阻。

发电机的数学模型为

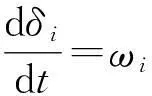
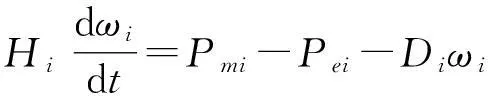
式中：Hi为转动惯量；Di为阻尼系数。现令

则当2发电机进行并联工作时，可推导出模型公式为：

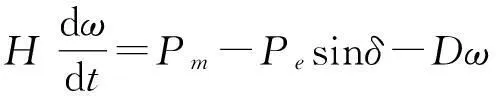
在系统运行时存在扰动，若扰动功率为：

ΔPe=ΔP·Pecos(βt)，

则模型可进一步推出：

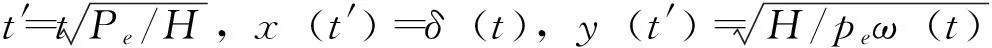
3.2　基于混沌现象的系统稳定性研究

本文对舰船电力系统的混沌分析采用基于反演的自适应算法，根据需要合理的设计一个判别状态特征的自适应控制器以对电力系统的状态行为进行预判并有效控制。

3.2.1反演自适应控制法

基于反演的自适应控制法的控制器设计原理即是在原扰动状态的非线性模型方程基础上加上一个输入变量u， 则扰动状态方程变为：

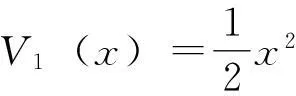
α1(x)=-k1x(k1>0)，

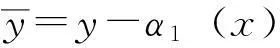
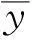
现定义李雅普诺夫函数为：

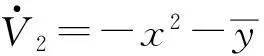
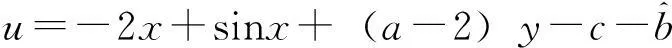
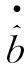
其中k>0。

在假如自适应参数控制器后，系统非线性动态模型为：

进一步转化后：

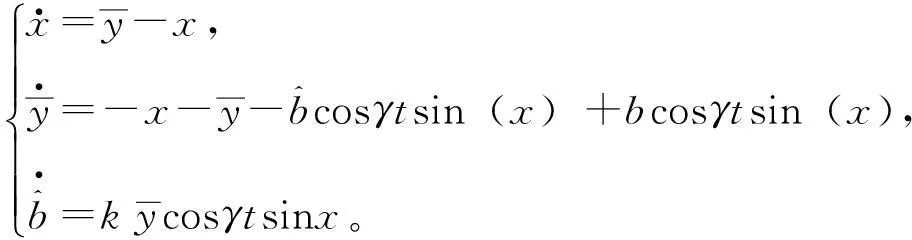
为了保证扰动幅值参数变量b在参数估计逼近调整后系统保持在稳定状态下，现取李雅普诺夫函数为：

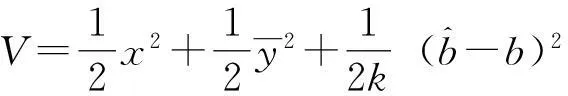
则

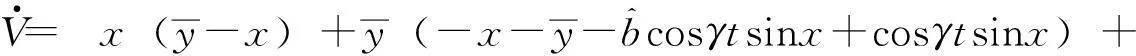
3.2.2仿真分析

仿真分析中，为保证结果与实际运行状态间的逼近，选取参数a=0.4，c=0.2，频率γ=0.8，并在系统状态出现非线性混沌震荡时及时加入自适应控制器u，更进一步分析系统的随后状态特征变化。在该仿真中，取幅值扰动参数b=1.3，功角δ和功角速度ω在系统运行时的状态如图5和图6所示。

图5　功角δ的状态曲线Fig.5　State curve of power angle δ

图6　功角速度ω状态曲线Fig.6　State curve of angle velocity ω

从图5和图6可知，当b=1.3，系统的前100s时，电力系统处于混沌状态；在假如自适应控制器u后系统逐渐趋于稳定，舰船电力系统的非线性混沌震荡得到很好的控制，系统运行达到了理想的状态。该仿真实现了对系统幅值扰动参数干扰的有效处理，说明反演的自适应控制法可以在舰船电力系统中进行应用，以抑制混沌震荡。

4结语

通过对幅值扰动对动力系统状态影响的模型分析可以看出，频率固定时，系统的幅值可能导致系统出现混沌现象，在利用反演算法有效引入自适应

控制器后，系统重新回归平衡状态。因此在舰船电力系统运行时，根据系统模型的分析可以对扰动因素选取合适的控制器参数保证系统处于稳定的运行区间，有效的避免陷入非线性的混沌状态，保证舰船的安全和可靠。

参考文献：

[1]徐成刚，梁世清.基于RHR算法的舰船电力系统混沌振荡参数计算[J].舰船科学技术,2013,35(8):86-91.

XUCheng-gang,LIANGShi-qing.CompdtationofchaoticoscillationparameterinshippowersystembasedonRHRalgorithm[J].ShipScienceandTechnology,2013,35(8):86-91.

[2]贾宏杰,余贻鑫,李鹏，等.电力系统混沌现象与不同失稳模式之间的关系[J].中国电机工程学报,2003,23(2):1-4.

JIAHong-jie,YUYi-xin,LIPeng,etal.Relationshipsofpowersystemchaosandinstabilitymodes[J].ProceedingoftheCSEE,2003,23(2):1-4.

[3]张卫东, 张伟年.电力系统混沌振荡的参数分析[J].电网技术,2000,24(12):17-20.

ZHANGWei-dong,ZHANGWei-nian.Analysisofparametersforchaoticpowersystem[J].PoulerSystemTechnology,2000,24(12):17-20.

[4]李文磊.不确定混沌电力系统的鲁棒自适应跟踪控制[J].电机控制学报，2007,11(2):170-173.

LIWen-lei.Robustadapativecontrolofchaoicpowersystenwithuncertainty[J].ElectricMachinesandControl,2007,11(2):170-173.

[5]黎古雄.基于混沌的电力系统模型研究[J].信息科学技术,2010(11):190-191.

LIGu-xiong.Researchonsystemmodelofelectricpowerbasedonchaos[J].ScienceandTechnologyInformation,2010(11):190-191.

[6]王涣文.舰船电力系统及自动装置[M].北京:科学出版社,2004.

Research on the stability of ship power system based on chaos analysis method

MA Hong-tao

(Jiangsu Maritime Institute,Nanjing 211170,China)

Abstract：This paper build the analysis modeling about ship power system first, and according to the characteristics of nonlinear chaotic model state of power system, combined with the model amplitude perturbation parameters, we analysis of causes and influencing factors of chaos phenomenon. On the basis of this, we use of adaptive inverse algorithm of introducing an appropriate controller in the model, it can effectively avoid power system to enter into chaotic state of shock and ensure safe and stable operation of the ship and the normal of shipboard power system. The results of the study show that, shipboard power system can effectively control the stability of the state according to its characteristics, to maintain the comprehensive performance of the ship, even if the chaos phenomenon exists.

Key words：chaos analysis；power system；comprehensive performance

作者简介：马洪涛(1978-)，男，硕士，讲师，主要研究方向为控制理论与控制工程。

收稿日期：2014-05-12； 修回日期： 2014-07-03

文章编号：1672-7649(2015)01-0152-05

doi：10.3404/j.issn.1672-7649.2015.01.032

中图分类号：U664.14

文献标识码：A