基于二次小波去噪的FastICA盲源分离研究*

赵 奎 黄高明

(海军工程大学电子工程学院 武汉 430033)



基于二次小波去噪的FastICA盲源分离研究*

赵 奎 黄高明

(海军工程大学电子工程学院 武汉 430033)

论文针对含噪声混合信号分离问题,提出了三步处理法,首先采用小波滤波进行去噪处理,再采用快速独立分量分析(FastICA)盲源分离技术实现混合信号的分离,最后对分离后的信号二次使用小波滤波处理。仿真实验结果表明,该方法能够很好地分离含噪混合信号,从分离前后的波形及平均信噪比对照,去噪性能和分离效果良好。

小波滤波; 独立分量分析; 波形; 平均信噪比

Class Number TN911

1 引言

盲源分离(Blind Sources Separation,BSS)技术是20世纪90年代中后期迅速发展起来的一种功能强大的信号处理方法,在不能应用参考信号或信号模型的前提下估计出原始信号。盲源分离作为人工神经网络、统计信号处理、信息理论相结合的产物,现已成为众多领域中研究与发展的重要课题,特别是在生物医学、语音与通信、图像处理、地球科学、计量经济学、文本数据挖掘等方面均有突出贡献[1]。

FastICA的盲源分离技术即是从观测到的混合信号中提取、恢复出无法直接观测的每个原始信号的过程,“盲”即是指源信号未知,并且混合系统特性也未知或是仅知道其少量先验知识(如非高斯性、循环平稳性、统计独立性)这两方面。该技术更适合于复杂电磁环境下的信号分离。传统的ICA算法在解决无噪或低噪情况下的混叠时,分离性能很优越,但当噪声较大时,分离效果则不好。

然而,复杂电磁环境下的信号往往是叠加有噪声的,小波变换可以将原始混合信号分解为一系列的近似分量和细节分量,信号噪声主要表现在信号的细节分量上。使用一定的阈值处理细节分量后,再经过小波重构就可以得到较平滑的与原始信号近似的信号。本文使用小波变换对各带噪混合信号进行预去噪处理,然后用FastICA的方法对去噪后的混合信号进行分离,最后再进行一次去噪处理,最终得到各个信号。仿真结果表明,此方法取得了较好带噪混叠信号分离。

2 带噪混叠信号模型

根据背景噪声与信号关系,噪声可分为加性噪声和非加性噪声。对于某些非加性噪声而言,可以通过相关变换转换为加性噪声。例如,某些与信号相关的量化噪声可以通过伪随机噪声扰动的方法转换为与信号独立的加性噪声。

信号处理中的加性噪声可以分为周期噪声、脉冲噪声、宽带噪声等,宽带噪声来源广泛,它和信号在时域和频域上都基本重合,只有在没有信号阶段,噪声分量才单独存在,因此对噪声的消除比较困难[2]。

论文中考虑的带噪混叠信号中的噪声均视为加性宽带高斯白噪声,其线性瞬时混叠信号模型为

x(t)=As(t)+n(t)

(1)

其中,x(t)=[x1(t),x2(t),…,xm(t)]T为m维观测信号;s(t)=[s1(t),s2(t),…,sm(t)]T是m维未知信号;A为未知混叠方阵;n(t)=[n1(t),n2(t),…,nm(t)]T为m维加性高斯白噪声。

3 分离过程

整个过程中,首先利用小波变换对带噪混叠信号xm(t)进行去噪处理,得到尽量“纯净”的信号ym(t)。然后对ym(t)进行去均值和预白化处理,再采用FastICA算法对去噪后并预处理的混合信号进行分离,得到分离信号,此时,再次应用小波滤波对分离后的信号进行滤波处理。

图1 分离流程图

3.1 小波去噪处理

小波变换具有多分辨率的特点,在时域和频域都具有表征信号局部特征的能力,适合分析非平稳信号。

在小波去噪处理中需要注意以下问题[3]:

1) 处理方法。软阈值法和硬阈值法是小波消噪阈值处理的两种方法。其中软阈值处理方法能够使估计信号具有和原始信号同样的光滑性,并且获得的信号不会产生附加振荡;而硬阈值处理方法通常会使估计信号产生振荡,并且信号欠光滑性。

2) 阈值选取。噪声是一种随机信号,其方差未知,实际去噪过程中必须先对阈值进行估计,阈值估计方法有:(1)固定阈值(sqtwolog)选择;(2)基于史坦(Stein)的无偏释然估计原理的自适应阈值选择;(3)启发式阈值选择;(4)极大极小阈值选择。

3) 小波基选择。小波函数具有多样性,经验与理论的分析表明,去噪的效果随着小波函数的变化而改变,信号的效果与小波函数的正则性及基函数波形与数据的结构相似程度有关。对称性好的小波不产生相位畸变,正则性好的小波易于获得光滑的重构曲线和图像,选择对称性和正则性均较好的小波系进行去噪能得到更好的去噪效果。

4) 小波分解层数确定。不同分解层数去噪效果不一样,合理选择分解层数。

此文中采用基于对称延拓法小波进行三层分解并用启发式软阈值进行小波系数阈值化处理。启发式软阈值法去噪更加彻底,能够将混叠噪声有效滤除,而且估计信号具有和原始信号相同的光滑性,并且得到的信号不会产生附加振荡。

3.2 快速独立分量分析算法

快速独立分量分析(FastICA)算法的计算过程运用了批处理的方法,但计算时运用了自适应处理方法,可以说是两种方法的结合。每次分离只提取一个源信号,接着将其从原始数据中去掉,然后对剩下的数据进行下一轮提取,可以采用Gram-Schmidt正交分解来实现。

对所有ICA问题都要作一定的假设和约束:

1) 源信号si(i=1,2,…,m)都是零均值的实随机变量,且在任意时刻相互统计独立。

2) 源信号数m和观测信号数n之间存在关系m≤n。

3)si(i=1,2,…,m)中只允许一个源信号满足高斯分布。

4) 对各源信号的概率分布略有些先验知识。例如,某些音乐信号具有超高斯(super-Gassian)特性(如拉普拉斯分布)。

用向量wi表示第i次投影时的投影向量,则信号分离模型为

(2)

式(2)中zi(t)是提取的第i个分离信号。投影向量wi需要选择使投影后数据间独立性最大的向量。并由大数定理可知,几个相互独立的随机变量之和也趋近于高斯分布。因此,提取的信号非高斯性达到最大时,信号间的独立性也最大。信号的非高斯性可用负熵来衡量,定义为任意概率密度函数和具有相同方差的高斯密度函数间的K-L散度:

=Hg(z)-H(y)≥0

(3)

根据非高斯最大化准则,将概率密度函数p(z)展开为

(4)

式(4)中:pg(z)是具有相同方差的高斯分布;F(i)(z)是满足如下条件的函数:

(5)

(6)

一般取N等于1和2,即取函数F(1)(z)和F(2)(z),F(1)(z)用来表示对称性,概率密度函数的非对称性,F(2)(z)用来表示在原点左右的双峰性。此时,负熵可按下式进行计算:

J(z)≈w1{E[F(1)(z)]}2+w2{E[F(2)(z)]

-E[F(2)(v)]}2

(7)

式(7)中:v与y具有相同方差的零均值高斯随机变量。当概率密度对称时可化简J(z)为

J(z)=E[F(2)(z)]-E[F(2)(v)]

(8)

J(z)=E[F(2)(z)]-E[F(2)(v)]+β/2(‖wi‖2-1)

(9)

对wi求导,有

(10)

函数f(z)是F(2)(z)的导数。当进入稳态时,式(10)所示导数为零,即

γE[tf(wiTt)]+βwi=0

(11)

对式(11)进行牛顿迭代法求解,迭代公式为

(12)

t是球化后的数据,近似有

E[ttTf′(wiT(k)t)]≈E[f′(wiT(k)t)]

(13)

将式(13)代入式(12)并化简可得快速独立分量分析算法:

(14)

当对多个源信号进行提取时,一般只需选取不同wi(0),进行迭代即可,但为了保证每次提取的都是尚未提取过的源信号,需要在迭代前进行正交化,目的是把已提取分量去掉。

综上所述:基于负熵的快速独立分量分析算法步骤为

1) 解球化矩阵W;

2) 任取wi(0),规定‖wi(0)‖=1;

3) 迭代,wi(k+1)=E[tf(wiT(k)t)]-E[f′(wiT(k)t)];

4) 正交化,并且归一化wi(k+1)=wi(k+1)/‖wi(k+1)‖;

5) 若wi不收敛,跳转步骤3),直至求解完成。

4 仿真结果分析

实验中包含了四组含噪信号,采样点数均设定为800点,将小波滤波后与FastICA算法用于盲信号分离有下图2为四组原始信号。假定矩阵A为方阵,在Matlab中矩阵A线性混合这四组即将分离的信号,查询得A为如下矩阵:

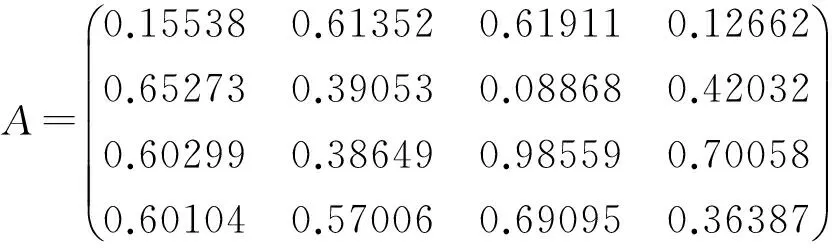
图2 四组原始信号

图3 观察的混合信号

图4 小波滤波后的混合信号

图5 分离后未再次去噪的信号

图6 分离后再次小波去噪

由图3和图4可以得出图4中经过小波滤波后的信号明显变得比图3中的信号噪声降低很多,由图2(s1、s2、s3、s4)为原始信号和图5(z1、z2、z3、z4)为分离出来的信号,其中原始信号s1、s2、s3、s4分别对应于分离后的信号z1、z3、z4、z2,信号的顺序作了一定调整,信号的大小和幅度也作了相应调整,但不碍于信号识别。

可以求得相似矩阵G相似矩阵G理想情况应为单位矩阵,可以看出G矩阵每行每列都有一个元素1,其余位置上的元素很小,可以近似看作0,并且可以得知矩阵存在一定误差,这也说明了原始信号s1、s2、s3、s4与分离信号z1、z2、z3、z4的对应关系和它们之间存在的误差。总的来说,可以得出应用小波滤波和FastICA算法分离得到的信号与原始信号相似度很高,可以得出结果。

图7 s1信号采样点数与平均信噪比

图8 s2信号采样点数与平均信噪比

图9 s3信号采样点数与平均信噪比

图10 s4信号采样点数与平均信噪比

进行500次实验,通过分析各含噪信号不同阶段的平均信噪比来量化该系统的性能。可以分别得到四个原始含噪信号信噪比、分离后未再次去噪信噪比和分离后再次去噪信噪比曲线图。对比可以得出:经过一次去噪处理和二次去噪处理的信号信噪比明显比原始含噪信号信噪比大几至几十dB,但二次去噪处理性能优劣程度与原始信号形式有一定关系,并且随着采样点数增加进行去噪处理后的信号信噪比有逐渐增大的趋势。

5 结语

本文介绍了基于小波滤波的自适应快速独立分量分析算法过程,并且应用于四个独立信号的盲分离,先通过小波滤波使混合信号尽可能平滑,然后通过FastICA算法分离滤波后的混合信号,再次使用小波滤波,通过从分离前后的波形比较及平均信噪比的比较,说明基于二次小波滤波的自适应快速独立分量分析算法是一种较好的信号分离方法,可以在语音盲信号分离中进行推广,具有一定的发展潜力。

[1] 史习智.盲信号处理—理论与实践[M].上海:上海交通大学出版社,2008:1-85.

[2] 刘琚,孙建德,许宏吉.盲信号处理理论与应用[M].北京:科学出版社,2013:117-119.

[3] 韦力强.基于小波变换的信号去噪研究[D].长沙:湖南大学,2007:14-15.

[4] 马晓红,殷福亮,陆晓燕,等.基于小波变换的传声器阵列语音增强方法[J].大连理工大学学报,2003,43(4):511-515.

[5] Hyvarinen A, Karhunen J, Oja E. Independent Component Analysis[M]. New York: Wiley,2001:147-161,293-304,391-406.

[6] 彭玉华.小波变换与工程应用[M].北京:科学出版社,1999:59-62.

[7] Potamitis I, Fakotakis N, Kokkinakis G. Speech enhancement using the sparse code shrinkage technique[C]//Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing,2001:621-624.

[8] Cardoso J F, Souloumiac A. Blind beamforming for non-Gaussian signals[J]. IEEE Proceeding-F,1993,140(6):362-370.

[9] Kotani M, Shirata Y, Maekawa S, et al. Application of independent component analysis to feature extraction of speech[C]//Proceeding of the IEEE International Joint Conference on Neural Networks,1999:2981-2984.

[10] 孙守宇.盲信号处理基础及应用[M].北京:国防工业出版社,2010.

[11] 万坚,涂世龙,廖灿辉,等.通信混合信号盲分离理论与技术[M].北京:国防工业出版社,2012.

[12] 余先川,胡丹.盲源分离理论与应用[M].北京:科学出版社,2011.

[13] 李正周.Matlab数字信号处理与应用[M].北京:清华大学出版社,2008.

[14] 陈怀琛.数字信号处理教程—Matlab释义与实现[M].北京:电子工业出版社,2004.

[15] 薛年喜.Matlab在数字信号处理中的应用[M].第2版.北京:清华大学出版社,2008.

FastICA Blind Source Separation Based on Secondary-wavelet Denoising

ZHAO Kui HUANG Gaoming

(School of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

A three-step method about noise mixed signal separation is put forward in this paper, the wavelet filter de-noising processing method and the fast independent component analysis(FastICA) blind sources separation technique to are used realize the separation, then the wavelet filtering method is used again to the separated signals. The simulation results show that the technique performs well in signal separation by comparing the waves and signal to noise ratio before and after separation and it has good denoising performance and separation effect.

wavelet filter, independent component analysis, waveform, average signal noise ratio

2014年12月5日,

2015年1月26日

赵奎,男,硕士研究生,研究方向:信号与信息处理。黄高明,男,教授,博士生导师,研究方向:盲信号处理。

TN911

10.3969/j.issn1672-9730.2015.06.011