航空器跑道滑行轨迹预测方法研究*

廖超伟

(北京西三环中路19号 北京 100841)



航空器跑道滑行轨迹预测方法研究*

廖超伟

(北京西三环中路19号 北京 100841)

为实现飞行间隔缩小,提升空域容量,需对航空器的运行轨迹进行精确预测,论文提出一种基于空气动力学的跑道滑行轨迹预测方法。该方法通过对在跑道滑行的航空器进行多自由度的受力分析,建立航空器滑行动力学模型,然后利用运动学理论建立航空器跑道滑行轨迹预测模型,实现航空器滑行轨迹预测。最后通过仿真案例验证了该预测模型的准确性。

跑道滑行; 轨迹预测; 动力学; 运动学

Class Number V351

1 引言

根据中国民航“十二五”计划提出建设现代空管服务系统的要求,基于4D航迹运行的空管自动化系统是空管系统未来发展趋势,其中航空器在跑道滑行预测模型研究是航空器4D航迹研究的重要组成部分,当前在轨迹预测领域主要有两种研究方法,一种是基于历史数据的航空器轨迹预测方法,另一种是基于空气动力学的航空器轨迹预测方法。第一类主要利用数据挖掘方法,研究航空器在跑道上运行规律,进而建立航空器运动学模型,该方法能够在大体上预测航空器运行轨迹,但是受飞行员个人因素影响较大,无法客观把握各类型航空器运行规律[1～2]。第二类方法也是当前最为通用的方法,但目前主要应用于航空器在空中运行时的4D轨迹预测[3～6],本文拟利用空气动力学理论建立航空器在跑道滑行时轨迹模型,进而能够较为准确地预测航空器在跑道上滑行状态。

2 航空器滑行动力学模型

航空器在跑道地面上运行,会受到各种因素的影响,顾宏斌等综合考虑了各类影响因素,建立了航空器在滑行过程中的六自由度受力模型[7],由于本文不考虑航空器在特殊状态下运行自由度,故本文只需建立航空器在地面上运行时三自由度的动力学模型,在建立模型前,有必要对前提条件进行假设。假设1:航空器为一个刚体,其质量变化只和燃油质量有关;假设2:跑道地面平整度一致,无颠簸。

航空器的欧拉角可确定航空器在空间中的方向,欧拉角分别用偏航角α、俯仰角β和滚转角γ表示。

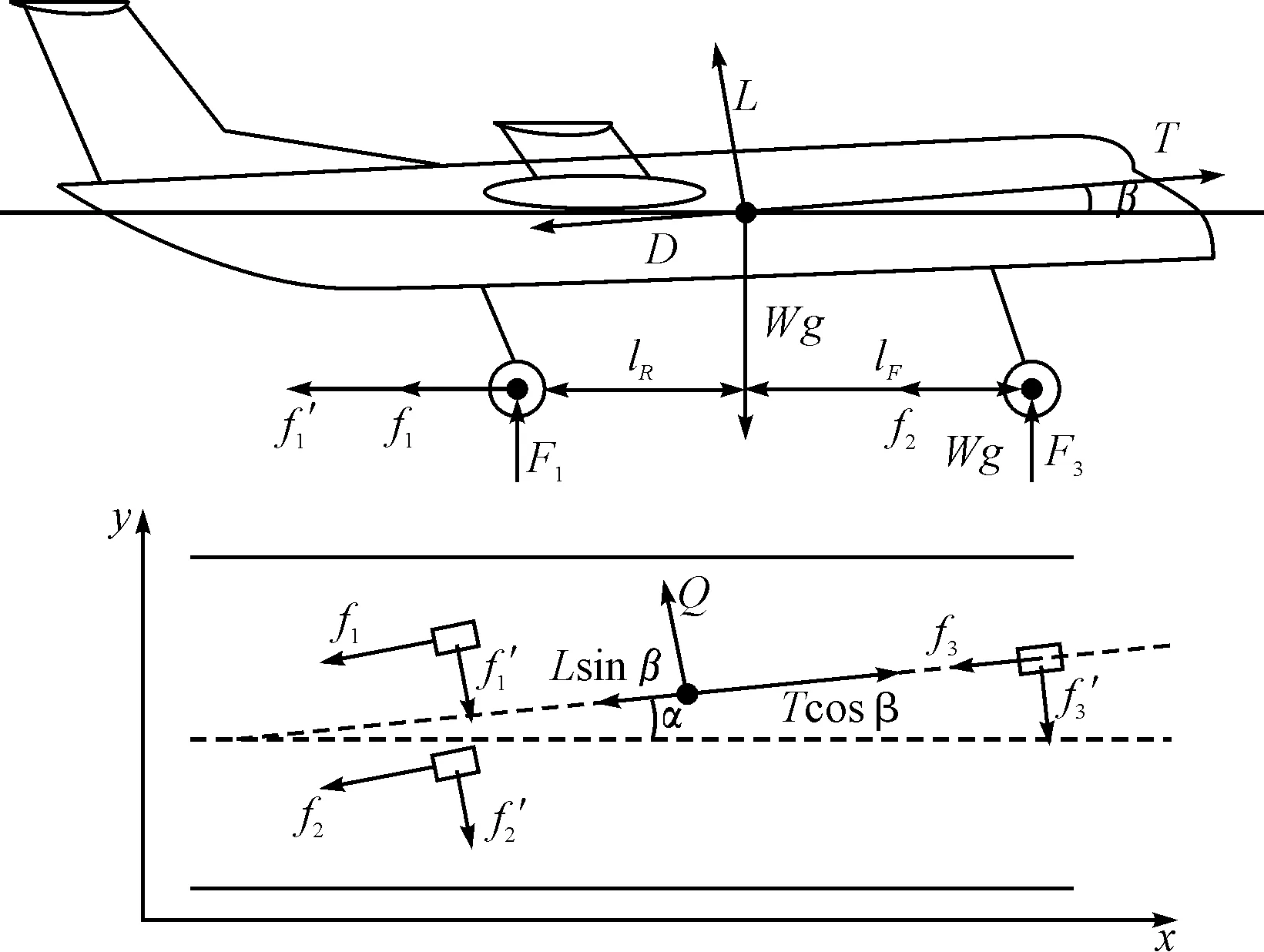
图1 航空器受力分析图

由于本文主要研究航空器地面滑行状态,故不考虑滚转角γ。假定航空器在地面滑行过程中,运行姿态正常,可假定滚转角γ=0,结合图1中所示受力分析以及公式,可建立该航空器在地面坐标系中三轴方向的平动方程:

Fx=Tcosβcosα-Dcosβcosα-Lsinβcosα-Qsinα

-f1cosα-f2cosα-f3cosα

(1)

Fy=Tcosβsinα-Dcosβsinα+Qcosα-Lsinβsinα

-f1sinα-f2sinα-f3sinα

(2)

Fz=Tsinβ+F1+F2+F3+Lcosβ-Dsinβ-Wg

(3)

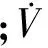
由于航空器在直线高速滑行过程中,如出现偏航角α,易导致航空器滑行发生危险,此类现象不属于本文探讨范围。假定航空器沿跑道或滑行道中线前进,无偏航,α=0,俯仰角β=0,为简化模型,同时忽略外界气候因素对航空器的影响力Q,故可建立航空器在地面坐标系中受力简化模型。

由于cosα=1,sinα=0,sinβ=0,cosβ=1,Q=0,故根据公式可推出:

Fx=T-D-f1-f2-f3

(4)

(5)

Fz=Tsinβ+F1+F2+F3+Lcosβ-Dsinβ-Wg

(6)

(7)

由于航空器整体无z轴方向运动,故航空器在纵向处于平衡状态,可知Fz=0,由此推出:

Fz=F1+F2+F3+L-Wg=0

(8)

其中:发动机推力T与航空器自身性能有关,并且不同的工作状态产生的推力也是不相同的。

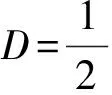
地面阻力f1、f2、f3取决于前后轮的支撑力F1、F2、F3的大小以及地面摩擦系数Cf,而前后轮的支撑力F1、F2、F3的大小取决于航空器的纵向力平衡和力矩平衡,前后轮到重心的距离分别为lF、lR。

因Fz=0,故:F1+F2+F3=Wg-L,根据力学平衡可知:

f1+f2+f3=Cf(F1+F2+F3)=Cf(Wg-L)

(9)

3 航空器跑道滑行预测模型

航空器在跑道头将油门加到起飞状态,松开刹车。航空器开始滑跑,待速度接近抬起前轮速度VR时,拉杆抬起前轮转为两点滑跑,该阶段滑跑时间很短,航空器自然离地,离地速度为VLoF,然后转入上升,上升到h=35ft时,速度达到规定的安全速度,至此航空器起飞过程结束[8～9],整个运动过程如图2所示。

图2 航空器起飞阶段模型

由于航空器在加速起飞过程中油门处于起飞状态,故可假定航空器所受推力不变,但空气阻力加大,故航空器速度一直加大,但加速度一直减小。

根据前面航空器在跑道上运行时的受力分析以及相关运动学理论,可利用如下公式推测航空器在跑道上滑跑速度:

(10)

(11)

(12)

航空器从静止开始加速,初始速度为0,待加速到离地速度VLOF时,航空器脱离地面,这一过程为航空器滑跑过程,其距离为l,可用以下公式推测出航空器滑跑位置:

l=∫Vdt

(13)

dV=adt

(14)

(15)

(16)

(17)

4 案例仿真分析

本文以B757-200型飞机为例,推测其在首都机场的第二跑道的起飞过程的轨迹。做如下假设:机场环境为标准大气压,无风,机场海拔高度为0m,空气密度为0.125kg·s2/m4,跑道无坡度。提取某日北京到昆明的领航计划报及BADA数据库[10],可以得到以下轨迹推测必要信息:飞机重量为100000kg,飞机全发工作,由于航空器滑跑时间较短,燃油消耗较少,可假定航空器滑跑过程中重量W不变,航空器起飞过程中参数取值如表1所示。

根据航空器起飞动力学模型,代入相关参数,利用动力学推测模型,取仿真时钟步长为Δτ=0.5s,可预测航空器起飞运动过程中速度随时间变化曲线如图3所示,以及航空器运动过程中距离随时间变化曲线如图4所示。

表1 参数取值

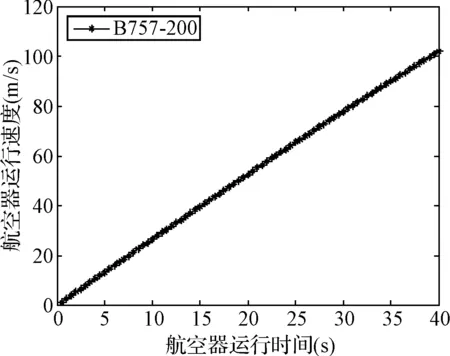
图3 预测速度随时间变化曲线

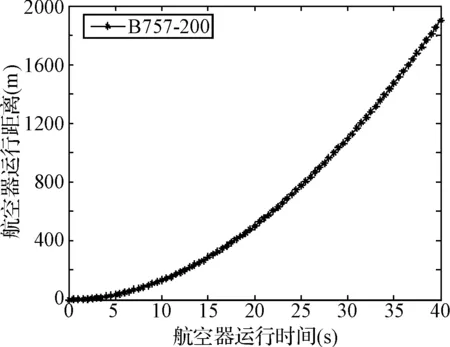
图4 预测运行距离随时间变化曲线

由图中仿真曲线可知,该曲线变化及数据与真实数据较为接近,可验证所建立的航空器起飞滑行运行学模型的有效性。

5 结语

本文通过利用动力学方法对航空器跑道滑行起飞轨迹进行了预测,建立了航空器滑行轨迹预测模型。在此基础上利用仿真工具对预测模型进行了实例仿真,仿真结果表明,预测模型准确度较高,接近真实值。

[1] Tang X M, Han Y X. 4D trajectory estimation for air traffic control automation system based on hybrid system theory[J]. PROMET-Traffic&Transportation,2012,24(2):91-98.

[2] 王超,郭九霞,沈志鹏.基于基本飞行模型4D航迹预测方法[J].西南交通大学学报,2009,44(2):295-300.

[3] 汤新民,韩云祥,韩松臣.基于混杂系统模型的航空器4D航迹推测[J].南京航空航天大学学报,2012,44(1):105-112.

[4] 彭瑛,胡明华,张颖.动态航迹推测方法[J].交通运输工程学报,2005,3(1):3-8.

[5] 罗兆文.基于GPS的飞机航迹预测方法研究[J].海洋测绘,2009,29(2):35-38.

[6] Tang X M, An H, Wang C. Conflict-Avoidance-Oriented Airport Surface-Taxiing Guidance Lights System Model[J]. Journal of Guidance, Control, and Dynamics,2012,35(2):674-681.

[7] 顾宏斌.飞机地面运行的动力学模型[J].航空学报,2001,22(2):163-167.

[8] 陈晨,周洲.无人机滑跑起飞过程及其数学模型研究[J].科学技术与工程,2007,7(13):3198-3201.

[9] 彭文华,卫平凡,刘国光.基于效能的舰炮武器系统RMS指标设计方法[J].舰船电子工程,2010,30(1):172-174.

[10] 丁毅萍.机场规划与运行分析[D].南京:南京航空航天大学,2009.

Prediction Method of Aircraft Runway Slide Trajectory

LIAO Chaowei

(No. 19 Central Road Xisanhuan, Beijing 100841)

In order to reduce the flight distance and improve the airspace capacity, the operation trajectory of aircraft should be accurately predicted. A prediction method of aircraft runway slide trajectory was proposed based on aerodynamics. The dynamic model of aircraft sliding was built by the multi dimension stress analysis of the aircraft, then the prediction model of aircraft runway slide trajectory was established to realize the prediction of aircraft runway slide trajectory by the kinematic theory. Finally, the accuracy of prediction model was verified by simulation.

runway slide, trajectory prediction, dynamics, kinematics

2015年2月3日,

2015年3月25日

廖超伟,男,硕士,工程师,研究方向:空管工程与技术、空管设备运行维护技术。

V351

10.3969/j.issn1672-9730.2015.08.034