基于CNS性能的飞行间隔安全评估*
贺文红
(北京西三环中路19号 北京 100071)
基于CNS性能的飞行间隔安全评估*
贺文红
(北京西三环中路19号 北京 100071)
为了有效地确定自由飞行下航空器之间的安全间隔,论文研究了基于通信、导航、监视性能的安全飞行问题。通过分别对所需通信性能、所需导航性能和所需监视性能进行分析,结合概率论相关知识建立了航空器之间的碰撞风险模型,并对不同飞行速度和飞行间隔情况下的碰撞风险进行了计算分析。结果表明两机水平间隔越大,碰撞概率越小;两机连线的飞行速度分量越大,所需的最小安全间隔越大。
空中交通管理; CNS性能; 飞行间隔; 碰撞风险
Class Number V321
1 引言
随着航空运输业的发展,我国的航空技术的不断进步,空中交通流量逐渐增大,空域日益拥挤。安全是民航的永恒主题,为了增加空域容量,满足流量需求,保障空中交通的安全有序,有关间隔安全评估的研究是必不可少的。
为促进空中交通管理系统在全球范围内的互用性和互通性,国际民航组织(ICAO)在推荐新的通信、导航、监视和空中交通管理系统技术的同时,一直在探索“所需性能”概念的建立与应用。因此提出了基于性能的通信导航监视(CNS)系统,其由所需通信性能(RCP)、所需导航性能(RNP)和所需监视性能(RSP)组成。国内外很多理论研究者从碰撞风险入手,通过建立碰撞风险模型来对飞行间隔的安全进行评估,因此在CNS环境下如何保证飞行安全成为一个研究热点。
在欧美等航空业发达国家,安全间隔方面的理论工作从20世纪60年代就已经开始进行了,最著名的是英国的Reich在20世纪60年代针对北大西洋地区平行航路系统在纵向、侧向和垂直方向分别建立了碰撞风险模型[1~3]。Peter Brooker分别提出了纵向间隔和侧向间隔的EVENT碰撞风险模型[4~5]。目前对于CNS性能环境下的碰撞风险研究处于起始阶段,国内有一些研究者已经开始对其进行研究,张兆宁、沈金炜等利用Reich模型和概率论的知识提出了CNS环境下的平行航路碰撞风险模型[6~8]。
本文对CNS性能下飞机的飞行间隔安全评估问题进行了探索研究,对同高度飞行情况下如何根据安全目标水平及CNS性能环境来设定相应的飞行间隔,建立了同高度飞行条件下基于CNS定位误差的碰撞风险模型,并利用Matlab对不同飞行速度和飞行间隔情况下的碰撞风险进行了计算分析。
2 碰撞风险模型建立
假设两架航空器在同一高度飞行,不妨设两架飞机初始水平间隔为D1,飞机在接下来的ΔT(ΔT很小,趋近于0)时间内,由于飞机的CNS性能环境造成两架飞机出现一定的定位误差,假设通信、导航、监视各自的定位误差是相互独立的,且根据文献[9],通信、导航、监视定位误差导致的偏航往往都服从均值为0的正态分布[10]。
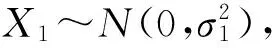
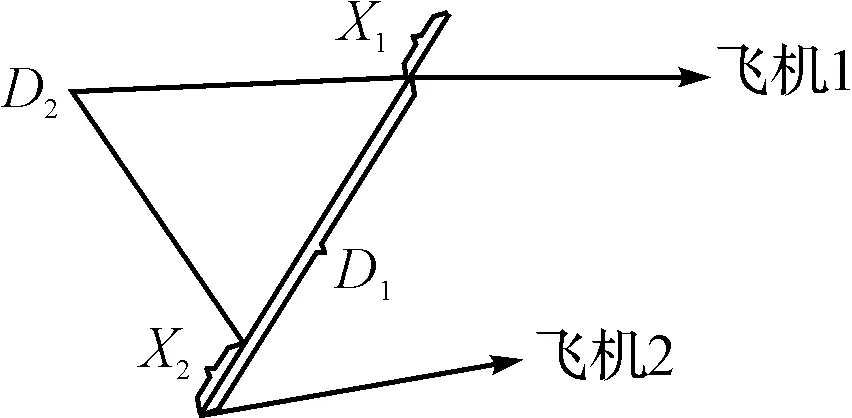
图1 同高度飞机距离示意图
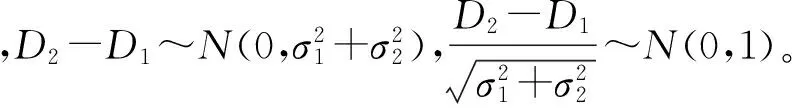
当同一高度层的两架飞机之间的水平间隔小于飞机尺寸L(L=max(机身长度,翼展长度))时,即认为飞机之间发生了碰撞,因此,两机碰撞的概率为
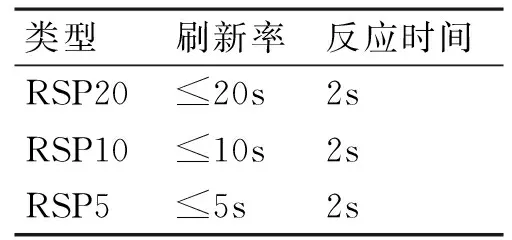
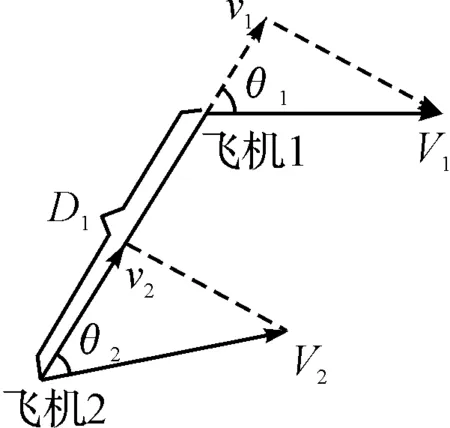
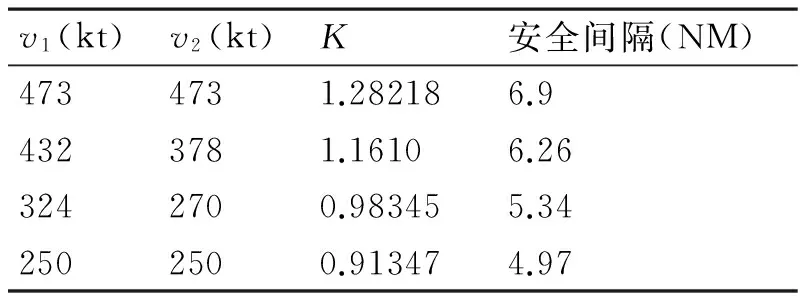
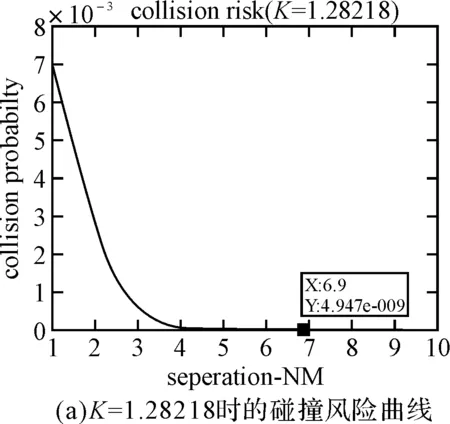
P(|D2| (1) 所以,要想求得碰撞的概率,就需要求解出定位误差σ(即σ1和σ2),从而需要确定CNS的性能参数。 CNS的性能环境主要分为所需导航性能(RNP)、所需通信性能(RCP)和所需监视性能(RSP)三个方面。 RNP是一种对空域和航路划分的判据,同时它是对进入该空域或航路飞行的飞机所需导航性能的要求。所需导航性能主要利用导航性能精度划分空域类型,表1列举了几种RNP的类型、参数和应用范围。 表1 RNP参数表 RCP是通常用处理时间、连续性、可用性和完整性来进行描述,表2给出了它的几种类型。 表2 RCP参数表 RSP是指在特定的精确度和刷新率条件下,得到航空器的速度、位置的能力,表3列举了几种RSP的类型和参数。 表3 RSP参数表 在此,CNS的性能参数分为RNPa、RCPb、RSPc三方面,其中a表示导航精度参数,单位为海里;b表示通信处理时间,单位为秒;c表示监视刷新频率,单位为秒。根据所需导航性能RNP、所需通信性能RCP和所需监视性能RSP的定义,有如下式子成立: (2) (3) (4) 上述式子中,v是飞机的巡航速度在两机连线上的分量,σ1、σ2、σ3分别表示导航、通信、监视所导致的水平间隔定位误差。由式(2)~式(4)可得: 2Φ(a/σ1)-1=0.95 (5) 2Φ(bv/σ2)-1=0.95 (6) 2Φ(cv/σ3)-1=0.95 (7) 从而求得: σ1=a/1.96=0.5102a (8) σ2=bv/1.96=0.5102bv (9) σ3=cv/1.96=0.5102cv (10) 综上所述,该模型的碰撞概率为 (11) 假设两架飞机的机型都是B737-200,安全飞行间隔为D1,其翼展长度为28.3m,机身长度为28.6m,所以飞机尺寸L取28.6m,即0.01544海里,两机飞行速度分别为V1和V2,速度方向与两机连线的夹角分别为θ1和θ2(图2)。因此,两机在连线上的速度分量分别为 v1=V1cosθ1 (12) v2=V2cosθ2 (13) 在此,令 以机载间隔保障系统为例,从机载间隔保障系统的导航性能来看,从美国公布的GPS定位精度已达到米级,所以GNSS已经符合RNP1的要求,所以参数a的取值为1。 供机载间隔保障系统使用的链路的传输率达到RCP10的要求,所以b的取值为10。 从机载间隔保障系统的监视系统(ADS-B)性能来看,它的更新率达到1s,报文延迟为0.4s~1.2s,所以ASAS符合RSP5的要求,所以c的取值为5。 因此,a=1(海里),b=10(s),c=5(s)。 所以,同高度的碰撞概率公式为 (12) 图2 两机速度和间隔示意图 B737-200的平飞最大速度为473kt(即飞机速度方向与两机连线的夹角为0时),当θ变化时,两机连线上的速度v1和v2会减小。结合同高度飞机碰撞模型,通过Matlab软件对D1从1海里到10海里变化情况下,针对不同的飞行速度进行计算分析(图3)。由于国际民航组织规定的空中碰撞的安全目标水平为5×10-9,因此可以得到不同K值情况下对应的水平安全间隔(表4)。 表4 不同的飞行速度对应的安全间隔 图3 不同K值所对应的碰撞风险变化曲线 从图3可以看出,两机水平间隔越大,两机的碰撞概率越小。从表4可以看出,两机连线上的飞行速度越大(K值越大),所需的最低安全间隔越大。所以在自由飞行的情况下,所需的最小安全间隔应当取K值最大时,所对应的安全间隔。 本文在给定安全目标水平及CNS定位误差导致的偏航分布下,建立了基于CNS定位误差的同高度航空器之间的碰撞风险评估模型,由仿真结果该模型及算法具有实际可行性。通过该模型及相应的算法,既可以在给定的安全目标水平及CNS定位误差下,计算相应的安全间隔,又可以根据安全间隔及CNS定位误差计算相应的碰撞风险,为以后深入研究CNS性能对碰撞风险的影响提供了一定的理论指导。 [1] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅰ[J]. Journal of the Institute of Navigation,1966,19(1):88-98. [2] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅱ[J]. Journal of the Institute of Navigation,1966,19(2):169-186. [3] REICH P G. Analysis of long-range air traffic systems: separation standards-Ⅲ[J]. Journal of the Institute of Navigation,1966,19(3):331-347. [4] Peter Brooker. Longitudinal collision risk for ATC track systems: a hazardous event model[J]. Journal of Navigation,2006,59(1):55-70. [5] Peter Brooker. Lateral collision risk in air traffic systems: a post-reich event model[J]. Journal of Navigation,2003,56(3):399-409. [6] 张兆宁,沈金炜,刘计民.基于CNS定位误差的侧向碰撞风险模型[J].交通运输工程学报,2009,9(6):110-113. [7] 沈金炜,张兆宁,刘计民.基于CNS定位误差的平行航路间隔安全评估[J].航空计算技术,2010,40(1):34-36. [8] 张兆宁,刘计民.基于CNS性能的垂直间隔碰撞风险评估[J].中国民航大学学报,2010,28(1):5-8. [9] DAVID E. STEPNER. Modeling of aircraft position errors with independent surveillance[J]. AIAA Journal,1973,11(9):1273-1279. [10] 王欣.空中交通中安全间隔问题的初步研究[D].南京:南京航空航天大学,2001. Flight Separation Safety Assessment Based on CNS Performance HE Wenhong (No. 19 Central Xisanhuan Road, Beijing 100071) In order to ensure the safety separation between the aircrafts under the free flight effectively, the safety flight problems based on the communications, navigation and surveillance performance is studied in this paper. The required communication performance, the required navigation performance and required monitoring performance are analyzed respectively, then the aircraft collision risk model is established combined with probability theory, and the collision risk is calculated and analyzed under the different circumstances of flight speed and flight separation. The analyzed result shows that as the horizontal separation of two aircrafts increases, the collision probability of two aircrafts is smaller. As the velocity component of two aircrafts attachment is greater, the required minimum safety separation is bigger. air traffic management, CNS performance, flight separation, collision risk 2014年11月5日, 2014年12月27日 贺文红,男,高级工程师,研究方向:指控系统。 V321 10.3969/j.issn1672-9730.2015.05.0093 CNS参数确定


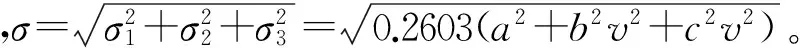
4 实例分析
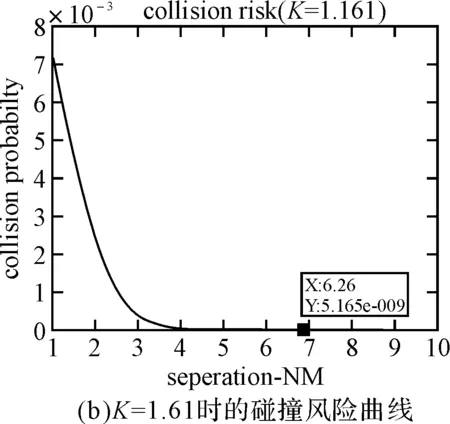
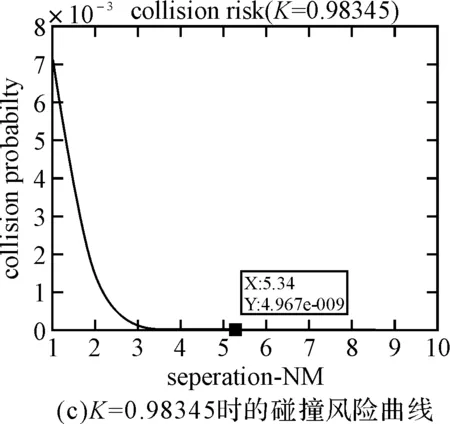
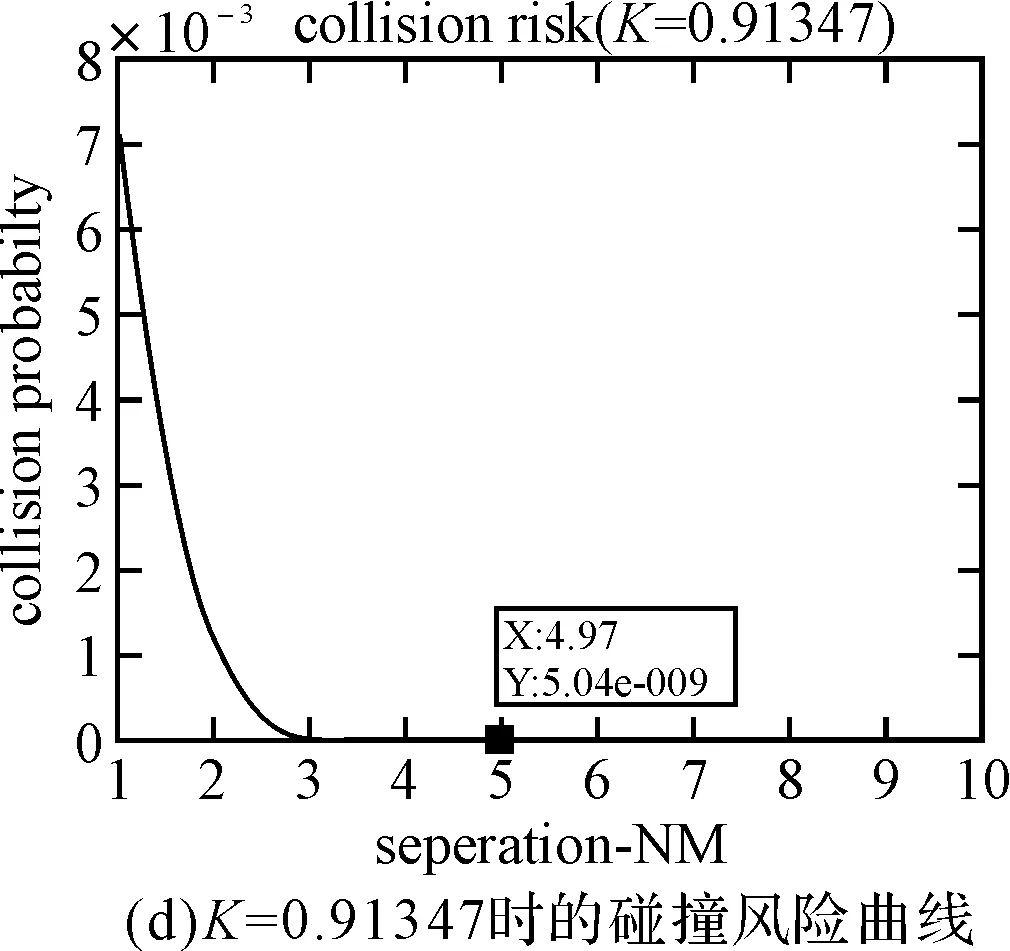
5 结语

