某船用齿轮结构拓扑优化设计

邱卉颖

(德州职业技术学院，山东 德州 253000)

某船用齿轮结构拓扑优化设计

邱卉颖

(德州职业技术学院，山东 德州 253000)

摘要：为提高某船用齿轮结构材料利用率实现其轻量化设计，将拓扑优化技术应用于齿轮结构优化设计。将齿轮截面作为研究对象，将其简化为一平面有限元问题。以齿轮单元密度作为设计变量，最大化齿轮结构刚度为目标函数，轮辐部分优化前后体积比作为约束，对其进行拓扑优化。研究不同轮辐数量、不同体积比情况下齿轮的结构传力路径。结果表明：轮辐部分体积比在0.4~0.6范围时，结构具有较好的刚度，并且加工工艺性优良。本文对于齿轮轮辐部分的拓扑优化结果为实际工程设计提供了指导。

关键词：拓扑优化；齿轮；轮辐；有限元

0引言

齿轮可分为车辆齿轮和工业齿轮。通常把直径介于500～3 000 mm的称为大型齿轮，是大型装备的关键零部件，广泛应用于发电、建材、船舶、矿山机械等重要领域，在国民经济和国防建设中具有不可替代性[1]。近年来，随着绿色环保等节能概念的提出，船舶结构轻量化设计引起人们的注意[2-3]。工业大齿轮的设计往往是根据标准进行选型，齿轮在工作过程中，部分材料应力小，材料的性能未能充分发挥，使得材料有所浪费，这种现象对于大齿轮的质量增加尤为明显。拓扑优化是一种基于有限元分析以及现代优化理论的优化方法，可根据给定的结构边界条件以及外载荷，对结构进行有限元分析，通过对有限元分析的结果对各单元应力进行灵敏度分析，将应力较小的单元删除，保留应力大的单元，最终形成最佳传力路径[4-5]。

为了对某船用齿轮进行轻量化设计，又不影响到整个传动系统的重新设计，本文将拓扑优化技术应用于齿轮结构的改型设计，在保证齿数、齿形等运动参数不变的情况下，对齿轮拓扑结构进行优化，为齿轮设计提供参考。

1齿轮参数建模

某船用齿轮结构参数如表1所示。根据齿轮参数采用Caxa软件对齿轮截面二维曲线进行生成，并以dwg格式导入ug三维建模环境，利用ug三维建模功能完成后续建模并以iges格式导入hypermesh进行有限元建模。

表1　齿轮结构参数

图1　齿轮几何结构Fig.1　The geometric structure of the gear

2有限元模型建立

为了一般性起见，本文将齿轮截面简化为一平面有限元问题，选用四节点壳单元以及三节点壳单元进行混合描述，单元尺寸选为6 mm。齿轮结构材料为45号优质碳素钢，材料弹性模量为E=200 GPa，密度取为7 800 kg/m3。为节约计算时间，在齿圈与腹板部分采用不同的单元尺寸，保证优化质量的同时，使得问题尽量简化。最终建立的有限元模型单元数量为9 702，节点数量为9 768，如图2所示。

图2　齿轮有限元模型Fig.2　The finite element model of gear

在齿轮与轴配合处，一圈单元采用reb-2单元进行耦合，采用驻点自动生成方式，即根据从点的几何中心放置主点。在施加扭矩时，在主点处加载200 N·m的绕z轴的扭矩。在一齿齿顶处约束其6个自由度。

3拓扑优化

拓扑优化是一种基于有限元分析以及现代优化理论的优化方法，其原理可简述为根据给定的结构边界条件以及外载荷，对结构进行有限元分析，通过对有限元分析的结果对各单元应力进行灵敏度分析，将应力较小的单元删除，保留应力大的单元，最终形成最佳传力路径。

结构应变能表示为：

式中，Ω为设计区域，为有限元模型中设计单元；ε(u)为结构在载荷F作用下的结构应变；u为结构在特定载荷下产生的位移，在此为一列向量；D为结构弹性矩阵；F为载荷向量，在该问题中为一单点扭矩。

则由结构平衡关系，可得系统平衡方程为：

KU=F。

式中K为结构总刚度矩阵，为一对称矩阵。

最终，结构应变能可表述为：

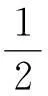
由于系统的柔度为：

C=FTU。

可知，当结构柔度最小时，可以获得最小的应变能，则刚度最大化问题可转化为最小化结构应变能问题。在建立结构拓扑优化模型前，首先对材料属性进行修改，并表述如下：

ρ(x)=xiρ0，

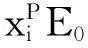
式中，ρ0为结构初始密度；E0为结构初始刚度；xi为引入的一个伪密度，其范围介于0和1之间，以此来表示材料的有无；P为惩罚因子，在此取为3。

则该拓扑问题可描述为：

设计变量：

x=(x1,x2,…xn)T；

目标函数为：

minc(x)=UTKU；

约束条件为：

KU=F，

0

式中：xi为单元伪密度；f为优化前后体积比，本文取0.1~0.6分别进行研究。

图3　拓扑优化过程Fig.3　Topology optimization process

拓扑优化过程如图3所示，该过程可大致描述为：首先建立齿轮结构有限元模型，提交有限元求解器进行应力计算。将计算结果与该优化问题的约束条件进行对比，看设计变量对应的响应是否满足约束条件,若满足约束条件，并且目标函数达到最优，则输出结构拓扑图；若不满足，则对结构进行敏度计算，对应力较低的单元进行惩罚，并重组有限元模型。重复以上过程，直至该优化问题的目标函数达到最优，并且满足约束条件。

在该齿轮优化中，齿轮与轴颈配合处以及齿圈部分引用非设计特性，齿轮轮辐部分引用设计特性，以此来实现对轮辐部分的拓扑优化设计。优化过程中响应为结构刚度以及体积比，该优化问题将最大化结构刚度作为目标函数，将结构优化前后体积比作为约束。

考虑到齿轮不同的轮辐数，本文在考虑加工工艺性以及经济性的前提下，对轮复数为3，4以及5时的情况分别进行研究，对每种轮辐数在不同的体积比下的拓扑结构进行研究，以供工程设计参考。

计算结果如图4~图6所示，其中图4为腹板数为3时的结构拓扑结果，图5为腹板数为4时的结构拓扑结果，图6腹板数为5时的结构拓扑结果。图中a~f为结构体积比从0.1~0.6逐渐变化。

图4　腹板数为3Fig.4　Webs number=3

图5　腹板数为4Fig.5　Webs number=4

图6　腹板数为5Fig.6　Webs number=5

当腹板数为3，并且体积比小于0.3时，结构明显偏于薄弱，在轻载工况可以考虑。对于重载情况，可优先考虑体积比为0.4~0.6范围的拓扑结构。相对而言，腹板数为3时，拓扑结构具有较好的工艺性。

当腹板数为4，并且体积比小于0.4时，结构偏于薄弱，建议用于轻载工况。此时，拓扑结构任然具有较好的工艺性。

当腹板数为5，并且体积比小于0.3时，结构偏于薄弱，在轻载工况可以考虑。对于重载情况，可优先考虑体积比为0.4~0.6范围的拓扑结构。此时，在齿圈部分产生了尺寸参数较小的类似于孔的特征，去除这些材料对于齿轮结构轻量化并不明显，在加工时可以不进行加工，以保证该结构加工经济性。

4结语

1)本文基于拓扑优化方法，对不同齿轮轮辐数量进行研究，讨论了不同轮辐数量在不同积极比约束下的齿轮结构，并对拓扑结果应用工况进行了探讨。结果表明：轮辐部分体积比在0.4~0.6范围时，结构具有较好的刚度，并且加工工艺性优良，可用于重载工况。本文对于齿轮轮辐部分的拓扑优化结果为实际工程设计提供指导。

2) 本文将齿轮结构进行了一般性研究，即将其简化为一平面圆盘结构，这样的拓扑结果对于其他的圆形并且传递扭矩的结构仍然具有一定的参考价值，可根据质量要求选择不同体积比的拓扑结构。同时，可结合加工工艺性要求，选择不同轮辐数量的拓扑结构。

参考文献：

[1]石照耀,林虎,林家春,等.大齿轮测量:现状与趋势[J].机械工程学报,2013,49(10):35-44.

SHIZhao-yao,LINHu,LINJia-chun,etal.Currentstatusandtrendsoflargegearsmetrology[J].JournalofMechanicalEngineering,2013,49(10):35-44.

[2]杨安礼,丁玉叶.从船舶舾装产品减重看船舶行业的节能减排[J].上海标准化,2010(1):105-107.

YANGAn-li,DINGYu-ye.Weightlossproductsfromtheshiptoseetheshipoutfittingindustryenergyconservation[J].ShanghaiStandardizationMonthly,2010(1):105-107.

[3]龙凯,左正兴,肖涛,等.连续体拓扑优化中的过滤算法研究[J].中国机械工程,2007,18(10):1171-1174.

LONGKai,ZUOZheng-xing,XIAOTao,etal.Researchonfil-teralgorithmappliedincontinuumtopologyoptimization[J].ChinaMechanicalEngineering,2007,18(10):1171-1174.

[4]耿楷真,马国伟,潘树国,等.结构优化方法及其在舰载武备结构设计中的应用[J].舰船科学技术,2007,29(S1):134-137.

GENGKai-zhen,MAGuo-wei,PANShu-guo,etal.Introductiontostructureoptimizationanditsapplicationtotheshipborneweapondesign[J].ShipScienceandTechnology,2007,29(S1):134-137.

[5]许辉,周奇,张立丽,等.基于混合优化策略的多学科协同优化及其应用[J].舰船科学技术,2014,36(11):23-28.

XUHui,ZHOUQi,ZHANGLi-li,etal.Applicationofanewcollaborativeoptimizationbasedonmixedstrategy[J].ShipScienceandTechnology,2014,36(11):23-28.

Topology optimization in marine gear optimal design

QIU Hui-ying

(Dezhou Vocational and Technical College,Dezhou 253000,China)

Abstract：In order to improve the utilization of marine gear structural materials to achieve its lightweight design, the topology optimization technology was applied to the gear structural optimization design. The gear section is simplified as 2-D finite element problems. Considering the element density as design variables, volume as constraint function, and maximize the structural stiffness as objective function of the topology optimization. The force transmission path is optimized under different spokes number and volume ratio. The results showed that: when the volume ratio of the spoke between the ranges 0.4~0.6, the gear will achieve good structural rigidity, and great convenience in manufacturing. In this paper, the topology optimization of gear spoke will provide guidance for the practical engineering design problems.

Key words：topology optimization;gear;spoke;finite element method

作者简介：邱卉颖( 1964 - ) ，女，副教授，研究方向为计算机辅助设计与制造。

收稿日期：2014-05-27； 修回日期： 2014-07-18

文章编号：1672-7649(2015)02-0176-04

doi：10.3404/j.issn.1672-7649.2015.02.039

中图分类号：TB114;TH132.41

文献标识码：A