基于MATLAB的圆形断面无压流特征水深的快速求解

黄邦右，马子普

（1.沧州水利勘测设计院，河北省沧州市交通北大街21－1号 061000；2.黄河水利委员会黄河水利科学研究院，郑州市顺河路45号 450003）

圆形断面是管渠工程设计及计算中常采用的断面形式之一，其正常水深和临界水深均为其重要参数，因此，水深参数的求解就显得非常重要。然而，关于两个水深的方程都是非线性超越方程，以目前数学能力尚难以得到解析解，因而只能采用近似解法。传统的近似解法有试算法、作图法，求解中费时费力且精度不高。针对这些问题，国内专家学者进行了深入研究，提出了多种圆形过水断面正常水深和临界水深的计算方法。赵延风等［1］对近年来国内多种圆形过水断面正常水深的计算方法［2－7］进行了详细的比较说明，张宽地等［4］，孙建等［8］，赵延风等［9］，分别提出了不同的圆形断面临界水深的直接计算公式。这些计算圆形断面水深的方法，无一例外都集中在采用迭代公式或推求合适的近似计算公式上。虽然这些方法很大程度上方便了实践问题的解决，但由于这些直接计算公式在推导过程中忽略了次要因素或应用范围受到限制，所以在应用这些公式时必然存在误差甚至错误，这是难以克服的局限性。

MATLAB具有很强的数据处理功能，灵活的插值方法，强大的图像显示和处理能力，是目前国际上最流行、应用最广泛的科学和工程计算软件［10］。MATLAB的独特优势使其可以直接对理论公式进行求解，这样就避免了模型误差，能够得到接近真值的高精度解。文中采用MATLAB语言对无压流圆形断面正常水深和临界水深进行编程计算，其编程代码接近数学推导公式，简捷直观，操作简单，人机交互性能好，而且效率和精度都非常高。

1 无压流圆形断面水深表达式

1.1 无压流圆形断面正常水深的函数表达式

由均匀流的基本公式［11］可推出：

对于圆形断面，过水断面面积：

湿周为

水深为

其中，r为半径，θ为过水断面圆心角（弧度），将式（2）、式（3）代入式（1），可得出未知量为θ的函数关系式：

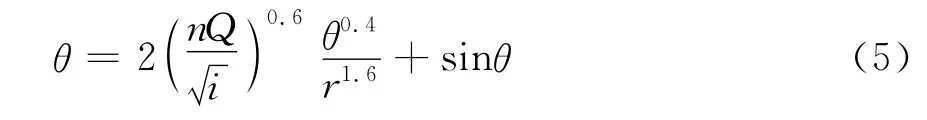
求出θ后，正常水深h可由式（4）求出。

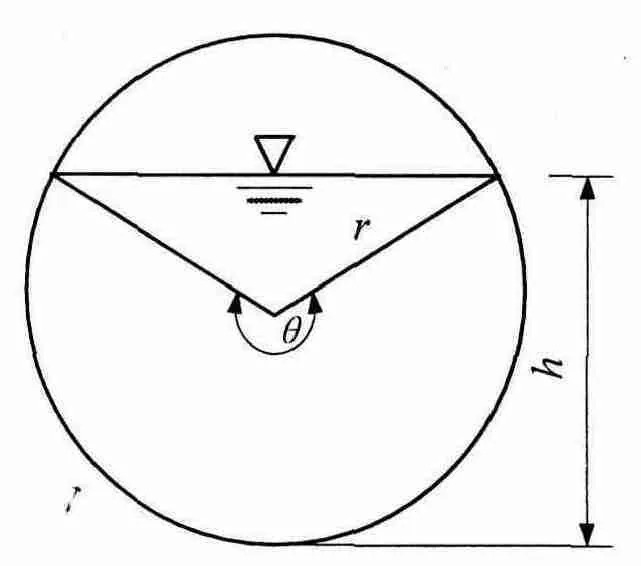
图1 圆形过水断面示意图

1.2 无压流圆形断面临界水深的函数表达式

临界流方程为

圆形无压隧洞过水断面面积为

过水断面宽度为

临界水深为

将式（7）、式（8）代入式（6），可得出未知量为θk的函数关系式：

求出θk后，临界水深hk可由式（10）求出。

2 应用举例

2.1 应用MATLAB语言编程计算正常水深

以文献［1］为例，某电站输水管道断面为圆形，已知断面底坡i＝0.001，糙率n＝0.015，断面直径d＝15 m，试确定流量分别为Q1＝840.0 m3／s和Q2＝0.2 m3／s时的正常水深。

（1）计算Q1＝840.0 m3／s时正常水深。暂用x替代θ，根据已知量求解无压流圆形断面正常水深的程序如下：

clc；

clear；

%创建符号变量及赋值

sy ms n Q I r x

n＝0.015；Q＝840；I＝0.001；r＝7.5；

%输入计算方程

f＝＠（x）2＊（n＊Q／I＾0.5）＾0.6＊（x.＾0.4）／r＾1.6＋sin（x）－x；

%求解过水断面圆心角

f＝fzero（f，［0.000001 2＊pi］）；

%输出结果

vpa（f，10）

ans＝4.263981468

即此时圆心角x为4.263 981 468 rad，继续应用式（4）编程求解正常水深：

%输入变量及赋值

r＝7.5；x＝4.263981468；

%输出正常水深

h＝r＊（1－cos（x／2））

h＝11.4915

即Q1＝840.0 m3／s时正常水深h＝11.491 5 m。

（2）计算Q2＝0.2 m3／s时正常水深。计算正常水深的程序如下：

clc；

clear；

sy ms n Q I r x

n＝0.015；Q＝0.2；I＝0.001；r＝7.5；

f＝＠（x）2＊（n＊Q／I＾0.5）＾0.6＊（x.＾0.4）／r＾1.6＋sin（x）－x；

f＝fzer o（f，［0.000001 2＊pi］）；

vpa（f，10）

ans＝0.4386609569

r＝7.5；x＝0.4386609569；

h＝r＊（1－cos（x／2））

h＝0.1797

即得Q2＝0.2 m3／s时正常水深h＝0.179 7 m。

2.2 应用MATLAB语言编程计算临界水深

【例1】以文献［9］为例，某水利工程的引水隧洞，设计泄流量为500 m3／s，拟用圆形断面，初设直径为15 m，试计算洞内的临界水深值。

【例2】某引水式电站输水隧洞为圆形断面，洞径15 m，试计算当水流流量为1 m3／s时洞内的临界水深。

（1）计算Q＝500 m3／s时临界水深。根据已知量求解无压流圆形断面临界水深的程序如下：

clc；

clear；

%创建符号变量及赋值

sy ms alpha Q g r x

al pha＝1.0；Q＝500；g＝9.81；r＝7.5；

%输入计算方程

f＝＠（x）（16＊alpha＊Q＾2／g／r＾5＊sin（x／2））.＾（1／3）－x＋sin（x）；

%求解过水断面圆心角

f＝fzero（f，［0.000001 2＊pi］）；

%输出结果

vpa（f，10）

ans＝2.854623623

即此时圆心角x为2.854 623 623 rad，继续应用式（9）编程求解临界水深：

%输入变量及赋值

r＝7.5；x＝2.854623623；

%输出临界水深

hk＝r＊（1－cos（x／2））

hk＝6.4276

即Q＝500 m3／s时临界水深hk＝6.427 6 m。

（2）计算Q＝1 m3／s时的临界水深。计算临界水深的程序如下：

clc；

clear；

sy ms alpha Q g r x

alpha＝1.0；Q＝1；g＝9.81；r＝7.5；

f＝＠（x）（16＊alpha＊Q＾2／g／r＾5＊sin（x／2））.＾（1／3）－x＋sin（x）；

f＝fzero（f，［0.000001 2＊pi］）；

vpa（f，10）

ans＝0.5439517126

r＝7.5；x＝0.5439517126；

hk＝r＊（1－cos（x／2））

hk＝0.2757

即得Q＝1 m3／s时临界水深hk＝0.275 7 m。

3 精度分析

文献［1］中针对上述实例比较了两种不同公式计算正常水深的相对误差，现将其与本文方法的计算结果进行比较，见表1。文献［9］中针对例1和例2比较了用诸家公式计算的临界水深的相对误差，现选取其中两种相对误差较小者与本文方法的计算结果进行比较，见表2。

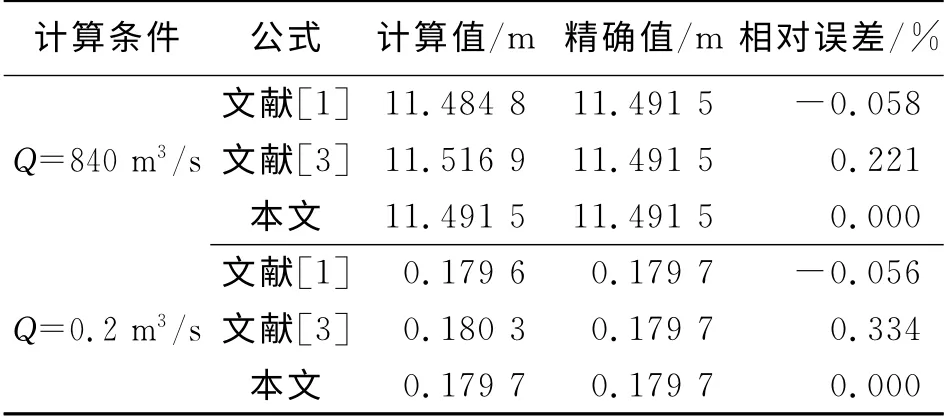
表1 正常水深不同计算方法误差比较

表2 临界水深不同计算方法误差比较

从表1和表2的误差可以看出，用本文方法求解的圆形断面的正常水深和临界水深，不仅求解过程较为简单，而且计算精度较高，特别是能满足小流量临界水深的计算问题。

4 结论

求解无压流圆形断面正常水深及临界水深，其关键是求其相应过水断面圆心角θ和θk的大小。文中采用MATLAB语言编程，快速得到圆心角值，再通过θ与h的关系式求得正常水深h，通过θk与hk的关系式求得临界水深hk，因它们都是直接采用理论公式进行计算，故精度较高。

［1］ 赵延风，祝晗英，王正中.一种新的圆形过水断面正常水深近似计算公式［J］.河海大学学报：自然科学版，2010，38（1）：68－71.

［2］ 吕宏兴，把多铎，宋松柏.无压流圆形过水断面水力计算的迭代法［J］.长江科学院院报，2003，20（5）：15－17.

［3］ 赵延风，芦琴，张宽地.圆形过水断面均匀流水深的近似计算公式［J］.西北农林科技大学学报：自然科学版，2008，36（5）：225－228.

［4］ 张宽地，吕宏兴，赵延风.明流条件下圆形隧洞正常水深与临界水深的直接计算［J］.农业工程学报，2009，25（3）：1－5.

［5］ 韩会玲，孟庆芝.非满流圆管均匀流水力计算的近似数值解法［J］.给水排水，1994（10）：25－26.

［6］ 王正中，冷畅俭，娄宗科.圆管均匀流水力计算近似公式［J］.给水排水，1997（9）：27－29.

［7］ 文辉，李风玲，黄寿生.圆管明渠均匀流的新近似计算公式［J］.人民黄河，2006，28（2）：67－68.

［8］ 孙建，李宇.圆形和U形断面明渠临界水深直接计算公式［J］.陕西水力发电，1996，12（3）：38－41.

［9］ 赵延风，何晓军，等.无压流圆形断面临界水深的新近似计算公式［J］.人民长江，2009，40（11）：76－79.

［10］ 郑阿奇.Matlab实用教程［M］.北京：电子工业出版社，2007：172.

［11］ 吕宏兴，裴国霞，杨玲霞.水力学［M］.北京：中国农业出版社，2002：187－189.