改进Simpson积分法在捕食模型参数辨识中的应用

范青 王昆明

摘 要：生产和科研中经常需要高精度地确定模型的参数，为此推导出了改进的变步长Simpson数值积分公式，并结合灰色系统理论，提出了一种模型参数灰色辨识的数学模型。采用此方法对捕食模型中的参数进行了辨识仿真，结果表明，基于变步长Simpson数值积分公式的灰色辨识方法在处理非等时间间隔以及数据波动性较大的参数辨识问题时稳定性较好，可满足高精度辨识模型参数的要求。

关键词：Simpson积分法 捕食模型 灰色理论 参数估计

中图分类号：Q332 文献标识码：A 文章编号：1672-3791（2015）08（c）-0235-03

捕食模型的参数辨识和仿真是一个经典的问题。文献记载了许多单种群Logistic模型参数辨识的曲线拟合方法[1-3]，但这些方法实际操作中存在一定局限性，向研究多种群模型的参数辨识推广比较困难，寻找确定2种群或多种群捕食模型参数的简便方法具有重要意义。文献[4]给出了2种群捕食模型参数的灰色估计方法，但此法基于等差或等间隔观察数据列，不适合任意递增的时间序列，观测数据波动性较大时，时间稳定性较差。该文基于拉格朗日插值公式，推导得到了变步长Simpson数值积分公式，并与灰色系统理论相结合，较好地处理了高精度辨识模型参数问题。

1 捕食模型及初值问题分析

自然环境中，生物种群之间通常存在相互竞争或相互依存或弱肉强食三种基本关系。著名的“弱肉强食”模型-捕食（Volterra）模型[5]为：

（1）

初始条件为：，为待定参数。

将（1）中两式相除，整理可得：

（2）

两边积分，得：

（3）

令 ，则有：

（4）

由（3）可见，初始条件，一定时，值是固定的。如果把，看作两个变量，那么它们之间的关系与捕食者、被捕食者之间数量的关系是相同的。因而在2个物种的数量达到某种稳定的循环时，作为初值条件的，可以是任何时刻的物种数量。一对，可以唯一决定一个循环状态。

2 变步长Simpson积分公式

文献[4]中利用了步长为单位时间间隔的梯形求积公式来估计参数，该文对其方法进行了改进，推导了具有较高精度的变步长Simpson积分公式。

常用数值积分公式是利用拉格朗日插值公式推出来的，拉格朗日插值多项式的一般表达式为：

其中称为拉格朗日插值基函数。

由两边积分，得插值型求积公式，其中为求值系数。

对于（1）中捕食者数量，考虑其在区间

上积分，且有，。记的积分为：

联立（5）、（6）可得：

，

当时，积分整理得：

代入公式（6）并化简可得：

上式即为基于拉格朗日插值公式的变步长Simpson数值积分公式。当时，（7）式可变为节点等距时的抛物线求值公式，。

3 捕食模型参数的灰色估计法

灰色理论[5]基于关联空间、光滑离散函数等概念，定义了灰导数和灰微分方程，是以定性为前提，定量为后盾，它采用离散数据列建立微分方程的动态模型，描述研究对象的动态行为，而且可直接对模型中的参数进行估计。

令，，，，则模型方程（1）可以改写为如下形式：

按导数定义有：

对于非负原始数据序列，采样间隔时间相对于种群数量的变化时间来说足够小时，近似地有：

写成离散形式为：

由（7）式，取时刻的背景值为：

t 时刻的背景值取法同上。灰色系统理论认为，微分方程是背景值与各阶灰导数的某种组合，那么（8）的第一个方程可被离散化为：。

将时的数据代入上式，可得矩阵方程：，

其中：，

在最小二乘准则下，可得方程组中第一个方程的参数估计值为：

同样道理，可以得到最小二乘准则下第二个方程的参数估计值：

其中：，

由前面分析可知，若观测值准确无误，那么任意时刻的观测值均可作为初值。

确定参数ak（1≤k≤4）后，若能够找到一组数，记，使得最小，便可确定最小二乘意义下的初值参数。

4 仿真与对比分析

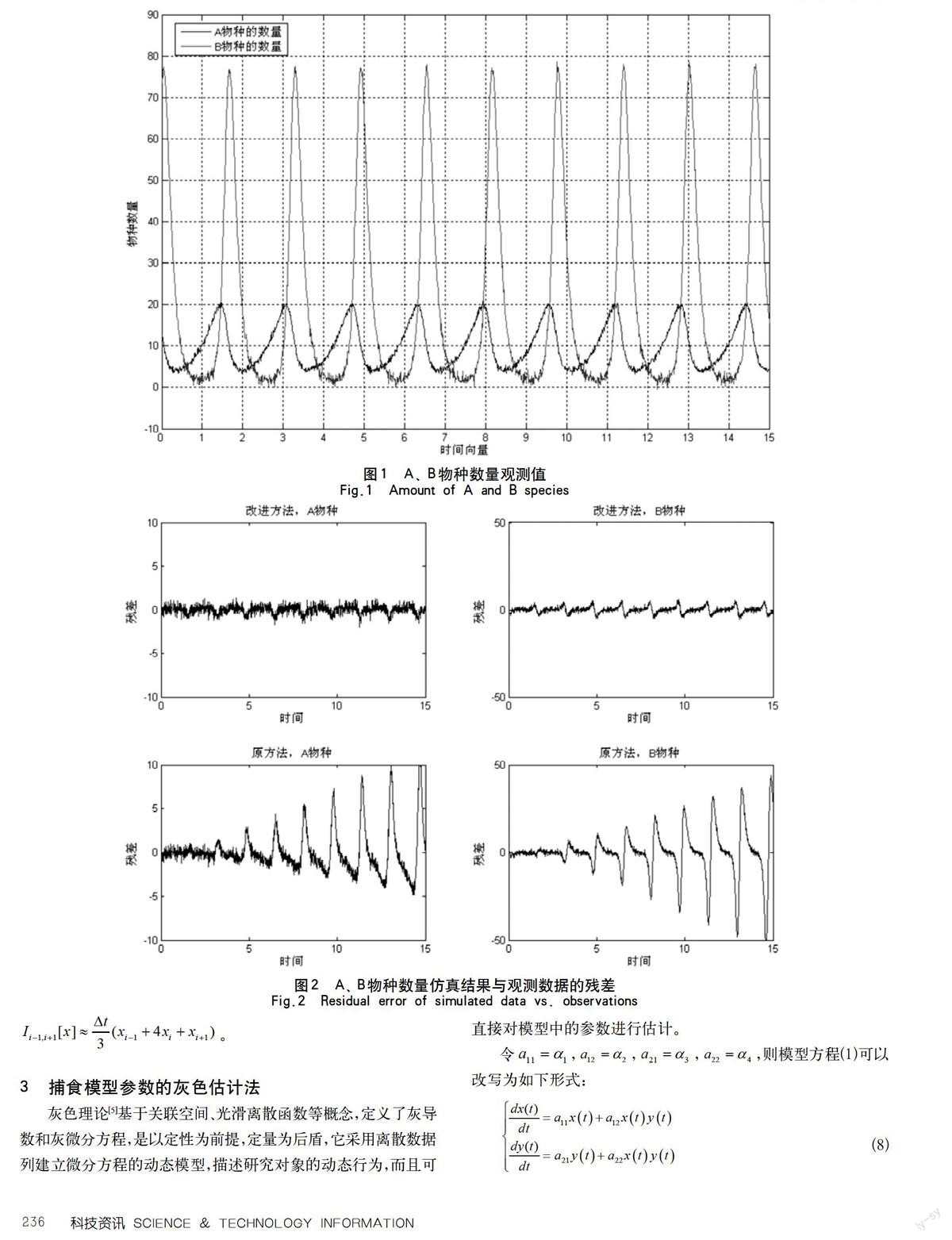
该文提出的基于Simpson积分公式的灰色辨识法，通用性较强，计算量小，可克服实际观测数据的不准确性带来的困难，易推广到多种群模型及其它类似模型参数的辨识问题。有某生态系统，含有两种生物：A生物和B生物，其中A生物是被捕食者，B生物是捕食者，图1给出了A、B物种数量的观测值，采用此数据进行模型参数的仿真对比分析。

从图1可以看出，由于观测点较密，数据的平顺性较差。为了达到更好的参数辨识效果，利用FFT滤波器对数据进行平滑处理。

基于处理后的数据序列，采用变步长Simpson积分公式的灰色辨识方法对模型参数进行辨识，通过MATLAB编程可以得到参数的估计值为：

近似采用原方法进行参数辨识，得到参数的估计值为：

将参数代入（8）中，利用四阶R-K法解微分方程组，将仿真结果与观测数据进行对比分析，其残差见图2所示。

从对比中可以发现，该文所给出的方法能够更好的符合观测数据，时间稳定性较好，不仅在初始阶段，而且经过几个周期之后，仍能保持与观测数据的同步变化；而原Simpson方法只能在初始观测时间段的附近区间较好的预测物种数量的大小和趋势。

5 结论

该文提出了一种基于变步长Simpson积分公式的灰色辨识方法，该方法简单，通用性强，稳定性高，只需要对给定的观测数据进行适当的代数运算，直接代入矩阵就可求得参数的估计值。分析计算结果表明，在参数估计问题中，该文的方法可以以较高的精度获得模型的参数估计值。

参考文献

[1] 殷祚云.Logistic曲线拟合方法研究[J].数理统计与管理，2002，21（1）：41-47.

[2] 王红春，陈平留.三次设计结合模失法拟合Logistic曲线的研究[J].生物数学学报，1999，14（4）：453-458.

[3] 孙全敏，王占礼，邵明安.生物种群Logistic扩展模型灰色增量生成参数辨识及应用[J].系统工程理论与实践，2000，15（8）：105-113.

[4] 李兴莉，申虎兰，冯玉广.Logistic和Volterra模型参数的灰色估计方法[J].大学数学，2004，20（6）：82-87.

[5] 王兵团.数学建模基础[M].北京：清华大学出版社，2004.