人体扫描线点云精简与孔洞修补

朱广舟，李晓久

(1.广东工业大学艺术设计学院，广东广州 510090;2.天津工业大学艺术与服装学院，天津 300160)

近年来，三维扫描技术的快速发展与应用使得利用高密度点云来精确描述人体表面成为可能。目前，可通过建立三维人体模型实现对人体表面拓扑结构和几何结构的细节描述，这些模型对服装行业尤其是数字化服装技术领域具有重要意义。通过建立三维人体模型可实现对人体精确、快速测量，可应用于人体生长监测、个性化服装批量定制、三维服装设计以及虚拟试衣等。

1 点云数据获取

本文基于双目立体视觉原理开发研制了一套便携式三维人体扫描系统［1］，系统主要硬件配置如表1所示。

表1 系统硬件配置Tab.1 Hardware of system

被扫描者身着紧身内衣站立在自动旋转台上，激光发射器自动定位于人体头顶上方距地面2.2 m高度并由上至下对人体进行扫描，处于上下不同位置的2台摄像机同步拍摄人体正面和背面的激光条纹图像［1］。

系统软件通过对人体正面及背面条纹图像进行预处理、相机标定、特征提取等步骤得到人体正、背面的点云数据;通过空间几何变换、立体匹配、点云重定位等操作，得到人体初始扫描点云模型［1-2］，如图1所示。

图1 初始扫描线点云模型Fig.1 Initial point clouds model

由图1可知，人体扫描点云模型由一组平行于扫描平面的扫描线组成，扫描线上的点沿扫描方向密度很大，而扫描线之间的点云相对比较稀疏。扫描线上高密度的点云将给后期处理带来不利影响，因此必须进行精简。

受扫描环境、系统算法本身缺陷等因素的影响，人体表面存在部分扫描盲区，有些扫描位置，如腋下、裆部等因遮挡而产生孔洞。另外，与地面平行的部位如肩部、头顶、脚等部位也常出现漏扫现象，这些原因使点云模型存在孔洞，重建人体表面前必须对其进行修补。

2 点云数据精简

点云精简是点云处理的一个基础步骤，可以去除原始点云数据中的冗余部分，得到一个精简的模型，有利于点云的后续处理和造型。

近年来，研究人员针对扫描点云数据精简进行了大量研究。Rogers和Adams应用相邻点之间的弦长来进行点云精简［2］。Lee等提出一种角度偏差鉴别法［3］，此法通过计算连续3个点间的角度偏差来决定是否保留该点。平雪良等［4］利用相邻两点间的距离作为参数来判别该点是否应该精简。

本文对男性扫描人体进行点云精简实验，通过实验对相关方法进行比较，其中采样法和包围盒法的简化速度较快，但简度和精度不能同时保证。而弦差法、曲率简化法等能有效保持点云细节特征，但是局部区域的简度过大造成精度过低而影响后续建模质量。

本文采用便携式三维人体扫描系统扫描并获得人体扫描线点云，根据分析采用宽度检测法对扫描线点云进行精简。具体操作如下:

1)选择合适的阈值T，T往往取值于扫描线对应的人体宽度D，依据公式T需在0.001D～0.02D之间来取值;

2)沿X方向将扫描线分成2个部分;

3)选择每个部分扫描线的第1个点作为标记点p1，其后有 m个点，其中第 r个点记作 pr。在X方向，宽度

4)按照以下方法比较hr与T(参见图2):如果在T范围内只有1个点，则保留该点;如果在T范围内有若干个点，则保留最接近T值的点，删除其余的点。

图2 宽度检测法Fig.2 Width decision method

应用宽度检测法，得到第2个点后，该点作为新的标记点，依此类推至最后一个点。精简效果取决于阈值T的选择，T值越大，被精简的点云越多。本文利用便携式人体扫描系统对男性人体进行扫描，应用宽度检测法进行点云数据精简实验，结果如表2所示。

为了保证精简后人体点云模型的细节特征，T应在一定的范围内取值。经过试验比较，当T=0.006 D时，人体点云被精简至61%，结果如图3所示。

表2 数据精简实验结果Tab.2 Pesults of data simplification

图3 精简后的人体点云模型Fig.3 Simplified point clouds model

3 扫描线点云孔洞修补

对点云孔洞修补目前主要有2种方法:一种是在三角网格面重构后，对三角网格面进行孔洞修补［5］，Pfeifle 等［6］采用三角细分算法对孔洞进行细分，并采用基于Delaunay的三角剖分方法在孔洞内部生成新的三角片;另一种是直接对扫描点云进行孔洞修补［5］，如 Pavel等［6］利用扫描点云的邻近点构造曲面来修补孔洞;陈志扬等［7］通过构造逼近的B样条曲面并在曲面上计算采样点作为新增数据点等。

本文对男性扫描人体点云进行孔洞修补实验。首先采用Delaunay三角剖分对扫描点云进行三角剖分，再应用插补方法对孔洞进行三角形插补。结果表明:扫描线点云在不完整(有孔洞)的情况下进行三角剖分难度极大，不可控因素很多，网格化后因本身的三角网格生成不佳对后期修补带来极大麻烦，因此，针对扫描线点云，应该先进行孔洞修补，然后再进行三角剖分及建模。

针对第2种方法，采用三次参数样条插值的方法对扫描线上的数据点进行全局数据的插值拟合。该方法基本能够实现对扫描线点云数据补缺，但每条扫描线均须建立不同的曲线函数，在运算效率上大打折扣。

如前文所述，人体点云模型由一组平行于扫描平面的扫描线组成，同一条扫描线上的点位于同一扫描平面内，这些点存在必然的内在联系，同一扫描线上的点在一定程度上处于一个空间灰色系统，因此，针对每条扫描线，建立空间灰色模型，利用原始点云数据预测新的点云数据，实现对扫描线的孔洞修补。

3.1 空间灰色模型的数学原理

灰色系统理论通过灰色生成来弱化原始数据序列的随机性以研究其内在的规律［8］，通过建立灰色生成序列的微分方程，实现对无序数据序列的预测［9］。

灰色系统理论主要通过灰色生成处理将原始无序数据序列变成有序数据序列，通过求解微分方程建立灰色动态模型［10］。灰色空间模型解决的是空间点序列问题［11］。

假设P是一组测量点序列，

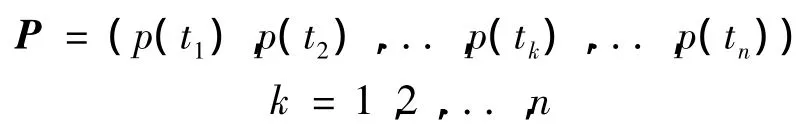
可以用以下数据序列表示原始数据序列:

一组新的数据序列可按以下公式生成:

然后建立微分方程:

数据矩阵B和向量Y如下:

通过求解微分方程，得到p(1)(k):

最后，通过累减生成计算预测值:

3.2 扫描线点云空间灰色模型SGM(1，1)

每条扫描线上的点通过其空间坐标信息(x，y，z)共同决定该扫描线的运动趋势。前述测量点序列P可用下面的向量表示:

由于扫描操作特征，同一条扫描线上的点具有相同的y坐标，所以，此处只关注不同点间的x和z坐标值，建立扫描线点云空间灰色模型SGM(1，1)。

3.2.1 坐标转换

根据灰色系统理论，数据序列为时间序列，要求数据序列不能为负值，因此，当测量点坐标值为负时，必须对其进行坐标转换。为便于处理，当数据序列p(tk)出现负值时，采用下面方法对其进行坐标转换。

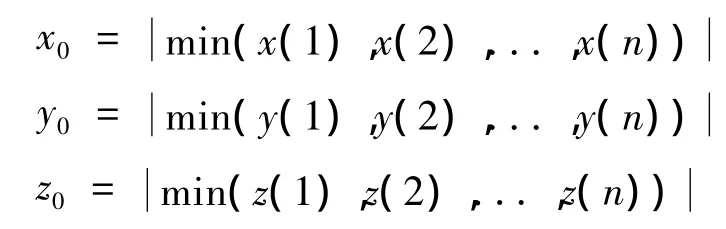
这样，测量点数据序列可表示为

3.2.2 孔洞检测

在进行孔洞修补前，必须先确定该条扫描线是否存在孔洞。根据扫描线特征，采用相临两点间弦长来进行孔洞检测。每条扫描线上相临两点弦长可构成下列数据序列:

式中d(1)代表p(n)和p(1)间的弦长。通过分析整理弦长数据序列，去除异常数据，取其平均值作为阈值来检测孔洞是否存在。若，则孔洞存在。

3.2.3 建立灰色空间模型SGM(1，1)

据上所述，通过孔洞检测，若存在孔洞，根据灰色空间模型基本原理，建立扫描线点云灰色空间模型为

试验中，每条扫描线上的点按顺时针读取。如果只有1个孔洞，则线上所有点用于建立模型;如果存在2个或2个以上的孔洞，则分段取点建立模型。每当1个新点生成时，需按照孔洞检测方法重新检测孔洞是否存在，以决定是否需要生成新的点。

当处理完所有扫描线，就完成对点云模型的孔洞修补，结果如图4所示。

4 结论

图4 孔洞修补后的人体点云模型Fig.4 Hole-filled point clouds model

本文利用自行研制的便携式三维人体扫描系统扫描并获得人体扫描线点云模型。受扫描环境、系统算法本身缺陷等因素的影响，原始点云数据存在很多不足，如点云密度过高、存在孔洞等。在进行人体表面重建前，必须进行有效处理。通过分析扫描线点云特征，采用宽度检测法进行点云数据精简，精简结果依赖于阈值T，当T=0.006D时，人体点云被精简至61%。针对孔洞修补，提出一种基于空间灰色系统理论的解决方法，建立扫描线点云空间灰色模型SGM(1，1)，有效地实现对人体扫描线点云的孔洞修补。

［1］ WANG Yuxiu， LI Xiaojiu. A portable body measurement system based on stereo vision［C］//LI Xiaojiu.Proc Int Text，Cloth Des Conf-Magic World Text，2008:686-691.

［2］ 李晓久，景晓宁.基于非接触式测量的人体点云简化方法［J］. 纺织学报，2012，33(7):144-148.LI Xiaojiu，JING Xiaoning.Study of body point cloud simplification based on non-contacted measurement［J］.Journal of Textile Research，2012，33(7):144-148.

［3］ LEE K，WOO H，SUK T.Data reduction methods for reverse engineering［J］.The International Journal of Advanced Manufacturing Technology，2001，17(5):735-743.

［4］ 平雪良，李进亮，徐荣礼，等.逆向工程中扫描线类型数据的简化技术［J］.江南大学学报:自然科学版，2006(3):258-260.PING Xueliang，LI Jinliang，XU Rongli，et al.Scan line data reduction for reverse engineering［J］.Journal of Southern Yangtze University:Natural Science Edition，2006(3):258-260.

［5］ LI Xiaozhi.Filling the holes of 3-D body scan line point cloud［C］//LI Xiaojiu. Proceedings of the 2nd International Conference on Advanced Computer Control，2010:334-338.

［6］ DU J，ZHANG L Y，WANG H T.Hole repairing in triangular meshes based on radial basis function［J］.Journal of Computer-Aided Design＆Computer Graphics，2005(9):1976-1982.

［7］ 吕莹莹，郝伟，郭金金.三维人脸模型孔洞修补技术研究［J］.计算机仿真，2012(1):195-198.LÜ Yingying，HAO Wei，GUO Jinjin.Hole-repairing of face model［J］.Computer Simulation，2012(1):195-198.

［8］ 刘思峰，郭天榜，党耀国，等.灰色系统理论及其应用［M］.北京:科学出版社，1999:75-208.LIU Sifeng，GUO Tianbang，DANG Yaoguo，et al.The Theory of Gray System and its Application［M］.Beijing:Science Press，1999:75-208.

［9］ ZHU Guangzhou.Gray modeling of hip girth based on the non-contacted human body measurement system［C］//LI Xiaojiu. Proceedings of the 2nd International Conference on Modelling and Simulation，2009:22-27.

［10］ 李晓久，朱广舟.人体胸围尺寸灰色模型建立［J］.纺织学报，2005，26(5):77-79.LI Xiaojiu，ZHU Guangzhou.Establishment the grey model of bust girth［J］.Journal of Textile Research，2005，26(5):77-79.

［11］ PING Xueliang， ZHOU Rurong， AN Luling.Application of grey system theory to processing of measuring data in reverse engineering［J］.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2003，20(6):36-41.