木棉及其混合纤维非织造材料吸声预测模型

刘雪亭，洪 杰，3，晏 雄，张慧萍

(1.东华大学纺织学院，上海 201620;2.东华大学纺织面料技术教育部重点实验室，上海 201620;3.江苏工程职业技术学院纺染工程学院，江苏南通 226007)

木棉纤维是天然的中空纤维，其中空度可以达到80%～90%。由于具有很高的中空度，木棉纤维常被用于隔热材料、水上救生材料以及吸声隔声材料等的加工。为便于材料的有效设计，必须理解并且能够预测木棉纤维的声学性能，但是目前对这方面的研究还鲜有报道。

有很多学者对纤维材料的吸声模型进行了研究，Zwikker-Kosten等［1］提出了完整的材料吸声理论，为后来各种材料吸声模型的建立提供了理论基础;Delany-Bazley等［2］拟合出声学上比较经典的流阻与吸声系数的经验模型;Allard等［3］采用等效流体的方法推导出刚性框架纤维材料内的声传播模型，该模型需要与纤维材料微结构相关的参数，而且比Delany-Bazley经验模型更加精确。还有很多学者对纤维材料的吸声模型进行了研究，Attenborough［4］、Manning 等［5］使用等效流体的方法研究了刚性框架材料的吸声性能，Wilson［6］、Michael等［7］、Garai等［8］从材料的微结构角度出发研究材料的吸声机制，但适用范围不够广。鉴于上述原因，本文以Allard模型为基础，建立一个适合于木棉及其混合纤维非织造材料的吸声模型。

1 木棉及其混合纤维材料吸声模型

1.1 Allard模型

Allard模型研究纤维材料内的声传播是将纤维材料视为刚性的多孔介质，主要参数包括:有效密度ρ(ω)、体积模量K(ω)。其中有效密度考虑了材料内空气与刚性介质之间的黏性效应，而体积模量考虑了材料内的热效应，有效密度及体积模量的计算公式［3］如下。

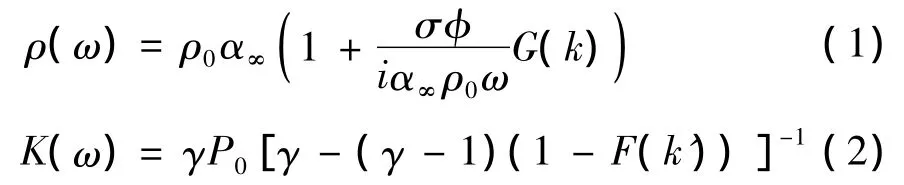
其中

式中:ω 为角频率，ω =2πf，f为频率;ρ0为空气密度;α∞为弯曲度;σ为材料流阻;φ为材料的孔隙率;γ为空气比热;P0为大气压力;Npr为普拉德常数;J0、J1分别为零级及一级贝塞尔函数，k为中间变量。常温常压条件下，ρ0=1.2 kg/m3，γ=1.4，P0=101320 N/m2，Npr=0.702。

纤维材料的特征阻抗Zc及传播常数χ［1］可通过式(7)、(8)计算。

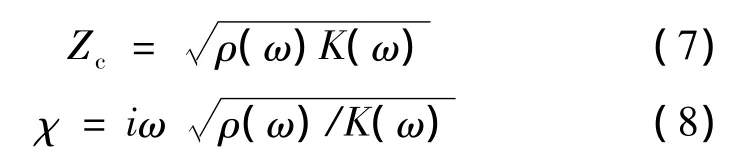
厚度为l的纤维材料的表面阻抗Zs及吸声系数α 可以通过式(9)、(10)计算得到［1］。

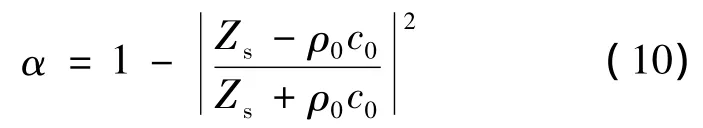
式中c0是声波在空气中的传播速度。

1.2 新模型的提出

Allard模型适用于刚性框架纤维材料的吸声性能计算，对于木棉纤维，由于具有最大的空腔结构(如图1所示)，与其他中空纤维相比木棉纤维内的静止空气更多，空间更大，从而木棉纤维的导热系数较小。Zwikker等［1］指出，黏性效应是由孔洞中的狭窄部分产生的，而体积模量(计算吸声系数的关键参数)是由热交换控制的。因此，需要进一步考虑木棉纤维的大中腔结构对吸声性能的影响。

图1 木棉纤维横截面的扫描电镜照片(×5000)Fig.1 SEM photographs of cross section of kapok fiber(×5000)

木棉纤维非织造材料的导热控制方程为

式中:E为木棉纤维的中空度;ρ0Ca为空气的体积热熔;T(r，ω)为温度函数;kaeff为空气的有效热传导系数;kaeff=ka×φ，ka为空气的热传导系数。

考虑到空气与纤维壁之间的热交换，界限条件为

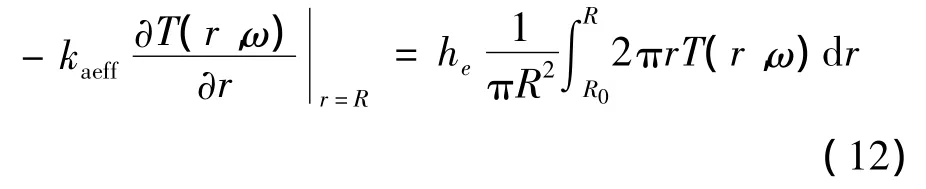
式中:he为热换系数;R为纤维半径;R0为木棉纤维的空腔半径。

根据式(11)、(12)，T(r，ω)可以推导如下:

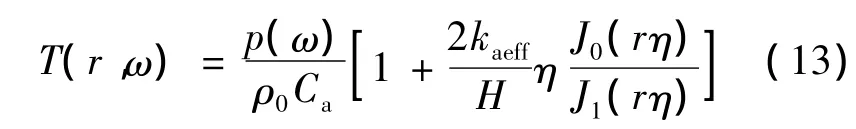
其中，

式中:p(ω)为压力函数;kf为纤维热传导系数，H和η为中间变量参数。

则体积模量K(ω)可以写成:

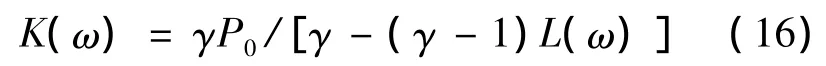
其中，

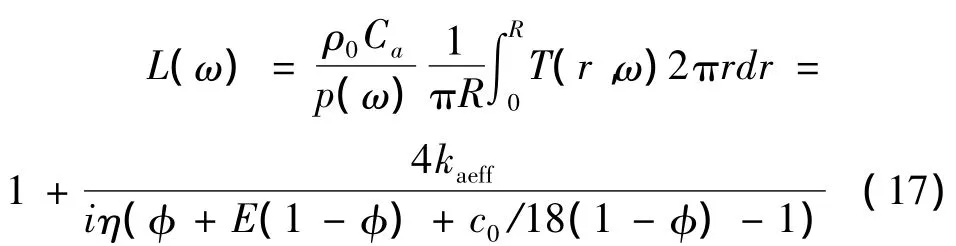
对于纤维材料来说，需要考虑纤维的柔软性，因此修正后的体积密度［9］为

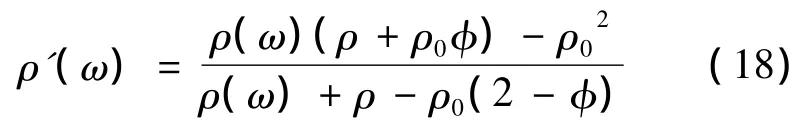
材料的比表面阻抗及吸声系数可以通过式(7)、(8)、(9)、(10)计算得到。

2 模型的检验

2.1 材料制备及实验测量

为证明模型适用于不同的木棉纤维非织造材料的吸声预测，制备了4种不同的实验样品，分别为木棉/中空涤纶、木棉/粘胶、木棉/丙纶(PP)及木棉/棉纤维，经过混合、铺网、针刺制备成非织造材料，所有样品中木棉纤维的含量均大于70%。木棉及其混合纤维非织造材料样品参数如表1所示。

表1 木棉及其混合纤维非织造材料样品参数Tab.1 Parameters of kapok-based nonwoven fabrics

吸声系数依据传播函数法及ISO 10534—2001《阻抗管吸声系数和阻抗测定》进行测量。测量仪器为北京声望公司生产的SW260阻抗管，每个样品测3次，取平均值。

2.2 结果与讨论

使用Allard模型及新模型对实验样品的吸声系数及比表面阻抗的计算值与实验测量值进行比较。图2示出4种不同组分及厚度的单层木棉及其混合纤维非织造材料样品的吸声系数的测量值与预测值(无空腔)。图3示出单层木棉/中空涤纶非织造材料样品的比表面阻抗的测量值与预测值(无空腔)。图4示出单层木棉/中空涤纶非织造材料在1 cm和3 cm背后空腔时吸声系数的测量值与预测值。图2～4示出样品在100～6300 Hz范围内的吸声系数及比表面阻抗的曲线。可以看出，木棉及其混合纤维非织造材料在整个频率范围内的新模型计算值比Allard模型计算值更加接近于测量值，进一步说明了新模型更准确地描述了木棉及其混合纤维非织造材料的吸声行为。这是由于新模型充分考虑了材料的结构特征(与热传导有关的)以及纤维框架的柔软性。

从图2还可以看出，在整个频率范围内新模型预测的吸声系数更接近于测量值。1.5 cm厚的木棉/中空涤纶样品，新模型预测的吸声系数与测量值之间的平均误差是0.027，对于2.0 cm厚的木棉/粘胶纤维样品是0.02，对于1.0 cm厚的木棉/PP纤维样品是0.016，对于0.9 cm厚的木棉/棉纤维样品是0.013。但是，Allard模型预测的平均误差分别是:0.04、0.042、0.035、0.036。图 2 表明新模型对于不同种类的木棉纤维非织造材料都适用。对4种木棉及其混合纤维非织造材料样品的比表面阻抗的测量值与预测值也做了比较，本文以木棉/中空涤纶材料为例(见图3)。图中，虚部表示声抗，实部表示声阻。图3表明新模型及Allard模型预测的比表面声阻都比较符合测量值，但是新模型预测的比表面声抗更接近于测量值。最后，对4种实验样品分别带1、3 cm背后空腔吸声系数的计算值与实验值也进行了比较，以木棉/中空涤纶材料为例(见图4)。可以看出，新模型预测的波峰对应的频率及吸声系数比Allard模型预测的更接近于测量值。由新模型计算的第1共振频率与测量值相差52 Hz，对应的最大吸声系数相差0.019。而Allard模型计算的第1共振频率与测量值相差102 Hz，对应的最大吸声系数相差0.038。尤其对于带有3 cm背后空腔的样品来说，新模型预测的波谷所对应的频率与测量值很接近，但是Allard模型预测的波谷所对应的频率及吸声系数却与测量值差距很大，由Allard模型计算的波谷处吸声系数远低于测量值。类似情况也出现在Kino［10］的研究中，这是由Allard模型中的低频与高频的限制条件造成的，Kino通过增加2个与流阻有关的修正因子对Allard模型进行了改善。

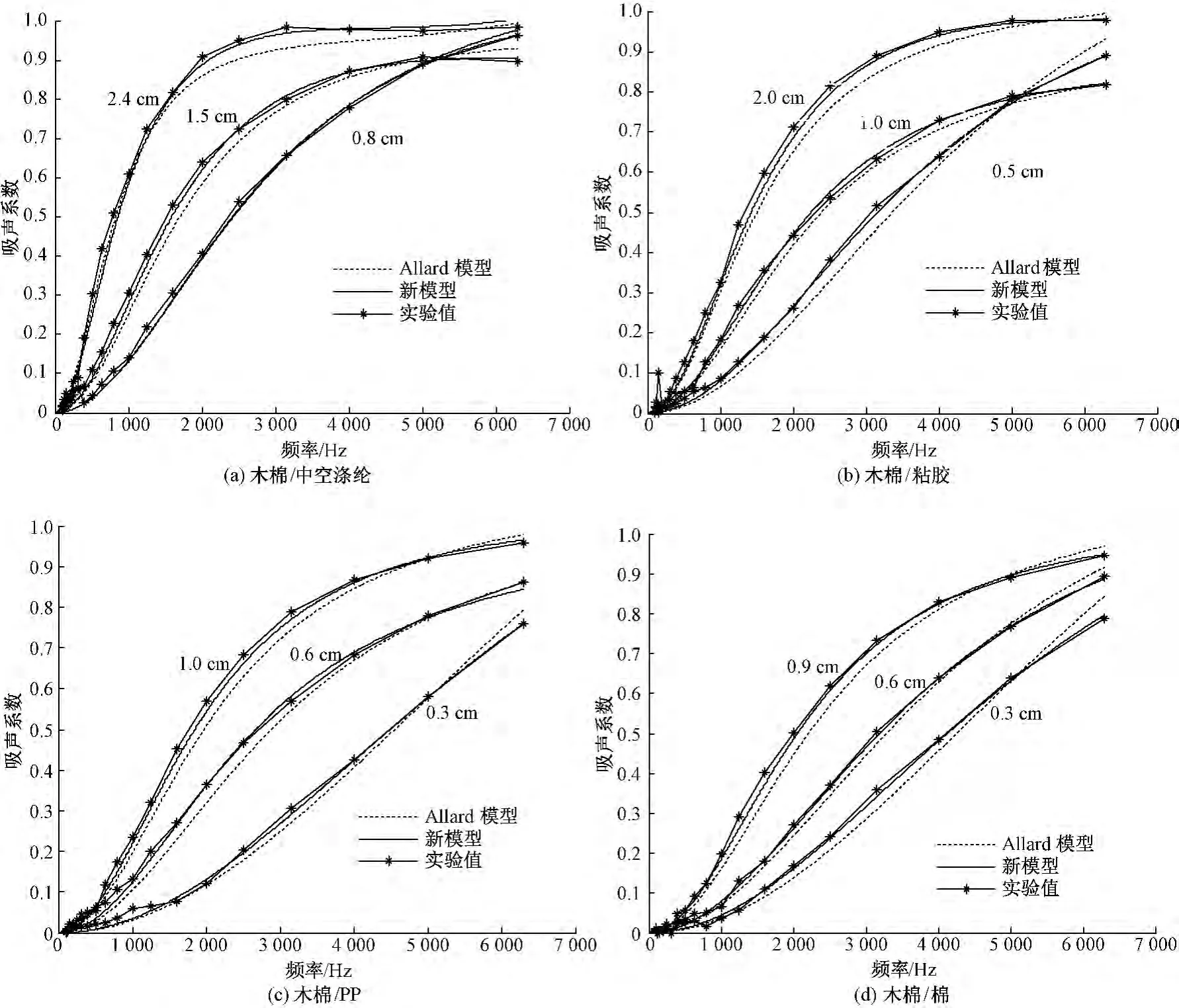
图2 4种不同样品的模型计算及实验测量的吸声系数比较Fig.2 Comparison of calculated and measured sound absorption coefficients for four types of kapok-based samples with different thicknesses.(a)Kapok/hollow polyester;(b)Kapok/viscose;(c)Kapok/PP;(d)Kapok/cotton

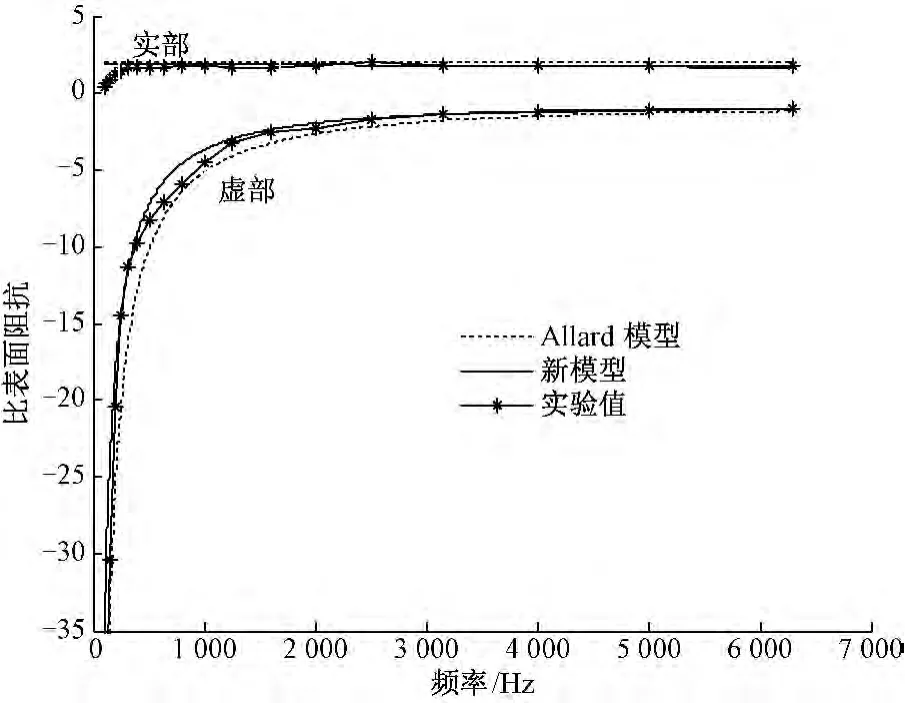
图3 木棉/中空涤纶非织造材料(厚度为1.5 cm)的计算及测量的比表面阻抗比较Fig.3 Comparison of calculated and measured specific surface impedances for kapok/hollow polyester samples with 1.5 cm thickness

图4 木棉/中空涤纶非织造材料(厚度为1.5 cm)吸声系数计算值及测量值的比较Fig.4 Comparison of calculated and measured sound absorption coefficients for kapok/hollow polyester samples with 1.5 cm thickness

3 结语

本文提出了木棉及其混合纤维非织造材料的吸声模型，该模型结合了木棉纤维的大中空结构，考虑了材料的热传导效应及纤维的柔软性。使用新模型、Allard模型分别对单层、带1、3 cm背后空腔的4种木棉纤维非织造材料样品的吸声系数进行计算并与实验测量值进行了比较，结果显示，新模型能够更加准确地描述试样的吸声行为。表明新模型可用于不同的单层及带有背后空腔的木棉及其混合纤维非织造材料吸声性能的表征。本文提出的新模型为今后木棉纤维材料的吸声机制的研究，尤其是低频吸声机制的研究提供了理论参考。

［1］ ZWILKER C， KOSTEN C W. Sound Absorbing Materials［M］.New York:Leiden，1949:1－75.

［2］ DELANY M E，BAZLEY E N.Acoustical properties of fibrous absorbent materials［J］.Applied Acoustics，1970(3):105－116.

［3］ ALLARD JF， CHAMPOUX Y. New empirical equations for sound propagation in rigid frame fibrous materials［J］.Journal of Acoustic Society of America，1992，91(6):3346－3353.

［4］ ATTENBOROUGH K. Acoustical characteristics of porous materials［J］.Physics Reports，1982，82(3):179－227.

［5］ MANNING J，PANNETON R.Acoustical model for Shoddy-based fiber sound absorbers［J］. Textile Research Journal，2013，83(13):1356 －1370.

［6］ WILSON D K. Relaxation-matched modeling of propagation through porous media，including fractal pore structure［J］.Journal of Acoustic Society of America，1993，94(2):1136－1145.

［7］ MICHAEL R S，CHAMPOUX Y.Propagation of sound and the assignment of shape factors in model porous materials having simple pore geometries［J］.Journal of Acoustic Society of America，1992，91(2):685－695.

［8］ GARAI M，POMPOLI F.A simple empirical model of polyester fiber materials for acoustical applications［J］.Applied Acoustics，2005(66):1383 －1398.

［9］ PANNETON R.Comments on the limp frame equivalent fluid model for porous media［J］.Journal of Acoustic Society of America，2007(122):217－222.

［10］ KINO N，UENO T.Improvement to the Johnson-Allard model for rigid-framed fibrous materials［J］.Applied Acoustics，2007，68(11/12):1468 －1484.