利用混合智能算法求解含分布式电源的配电网无功规划问题
卓定明,王增煜(.广东电网有限责任公司惠州供电局,广东惠州 56000;.广州供电局有限公司,广东广州 50000)
利用混合智能算法求解含分布式电源的配电网无功规划问题
卓定明1,王增煜2
(1.广东电网有限责任公司惠州供电局,广东惠州516000;2.广州供电局有限公司,广东广州510000)
摘要:提出了一种求解基于机会约束规划理论的含分布式电源配电网无功规划问题的方法,引入随机变量来表示风速,建立了基于机会约束规划的数学模型,利用随机模拟、支持向量机、粒子群算法相结合的混合智能算法进行求解。在含风机的IEEE33节点系统上进行算例分析,结果表明该方法具有较高的决策效率和计算精度,从而验证了所提出模型和方法的合理性和有效性。
关键词:间歇性分布式电源;配电网;无功规划;机会约束规划;混合智能算法
0 引言
近些年来,由于传统能源形式所凸显的弊端越来越明显,风能作为一种绿色的循环能源,具有较好的环保性跟经济性,以风力发电为代表的间歇性分布式电源在中国得到了迅速发展。新能源普遍具有波动性、间歇性和随机性的特点,当越来越多的分布电源接入配电网之后,改变了网络结构,将配电网系统从较为简单的无源网络转变成复杂的有源网络,系统运行状态的不确定大大增加,系统潮流发生变化,系统的无功功率需求将进一步增长,此时对含分布式电源的配网进行合理的无功规划至为关键。
由于配电网无功规划问题本身就是一个非线性、离散化的优化问题,并入分布式电源之后,该问题就难以用常规的数学方法进行分析了,主要原因便是风力发电机的有功输出具有很强间歇性和随机性,因此在某一确定场景下寻优得到的无功规划方案,在另外一些场景时不一定是最优规划方案,甚至有可能使得系统的潮流分布更不合理,严重影响到电网安全经济运行,因此传统的确定性规划对于处理随机变化的风电出力并不合适。在含分布式电源的配电网无功规划问题上,国内外学者已有了一定的研究。文献[1]考虑了静止无功补偿器作为补偿设备,综合有功网损和补偿设备的安装及生产费用作为目标函数,建立无功规划模型,但由于SVC设备昂贵,实际中还未广泛投入使用。文献[2]采用遗传算法对分布式电源无功优化问题进行求解,但仅仅考虑风力发电机在某一场景下的情况,在其他场景下未必最优。文献[3]提出了一种基于场景发生概率的无功优化综合指标,考虑了网损和静态电压稳态裕度,采用自适应权重的遗传算法求解问题。文献[4]以风力发电机的有功输出期望值近似代替随机变化的输出功率,用三种负荷运行方式代替近期的运行状况,利用NSGA-Ⅱ算法进行求解。
本文提出的无功规划方案充分考虑到了风速的随机性及其统计特征,将含分布式电源无功规划问题作为不确定规划问题进行研究,以网损费用和电容补偿设备投资安装费用最小化为优化目标,选取补偿装置的安装位置和容量大小作为优化变量,约束条件包括系统潮流方程约束、可调变压器变比上下限约束、无功补偿容量约束以及某一置信水平之下的节点电压上下限约束,建立基于机会约束规划的无功规划模型,并利用蒙特卡洛模拟法求解各类随机场景下安装补偿电容器的优化方案,这样便能够考虑多种可能的运行方式,而不仅仅是典型运行方式,由于采用概率形式表示电压约束条件,避免出现考虑确定性约束条件时优化结果过于保守的情况。同时为了减少系统潮流计算次数以达到提高求解速度的目的,设计了混合智能算法,将训练好的回归拟合函数代替费时的潮流计算过程,在计算精度不受太大影响的前提下,大大提高了粒子群算法优化迭代的速度,缩短了程序运行时间,本文将该算法运用到具体案例中,得到了不错的优化效果。
1 风电场随机输出功率的计算
一般认为,由于风速等气象条件的随机性,与风速有着很大相关性的风机有功输出是不可控的随机变量,目前已有该领域的众多研究人员对随机风速的分布特性展开了深入分析,一般可认为风速服从Weibull分布从而对风力发电力的随机出力情况进行数学建模[5]:

其中c和k分别为尺度参数和形状参数。
风电发电机有功输出功率PWPG与该点的风速v间的函数关系可用式(2)的分段函数近似描述:
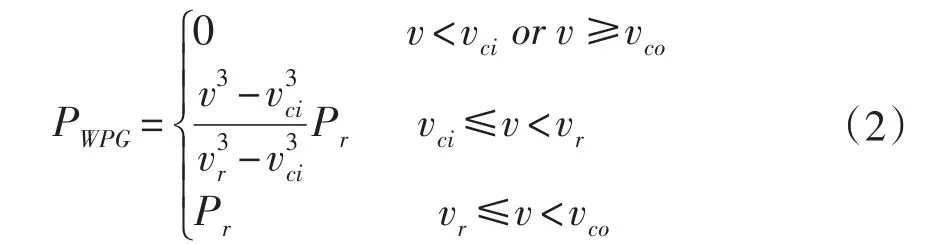
其中,Pr表示风机输出的额定功率,vr,vci,vco则分别表示风机运行时的额定风速、切入风速跟切出风速。
2 基于机会约束规划的无功规划数学模型
随机机会约束规划(Stochastic Chance-Const⁃rai-ned Programming,SCCP)是由Cooper和Charnes联合提出的一种随机规划模型[6],其核心是规划模型中的随机机会约束条件至少需满足某一给定的置信水平。机会约束规划是随机规划领域的重要内容,可在一定的置信水平下求解含有多个随机参数的随机规划问题。
随机机会约束规划模型通常表示为:

其中,x和ξ分别是模型的决策和随机变量,pr{ }表示某事件发生的概率,α和β分别是决策者给出的各约束条件和目标函数的置信水平,fˉ则是模型的目标函数f( ) x,ξ在满足目标函数置信水平至少为β时所能达到的最大值。
2.1目标函数
本文综合考虑了含分布式电源配电网运行时的有功网损、无功补偿电容装置投资运营经济性,以并联电容补偿容量的投运组数和无功补偿装置的安装地点作为控制变量,考虑潮流约束、电压上下限约束、可调变压器变比的上下限约束和无功补偿容量约束来建立规划模型。由于无功补偿设备的投资费用是一次性的,需将其转换为等年值。
因此,本文的优化目标为:

其中,Δpi为系统有功网损,常数k为单位能耗费用,n为系统总节点数,τmax为负荷运行小时数,ei为0-1变量,决定各节点是否安装并联补偿电容器组,ri为节点i安装单位补偿电容器组的费用(包括购买、安装费用),Qci为节点i的补偿电容容量,a为贴现率,m为补偿设备的使用年限。
2.2约束条件
(1)潮流等式约束
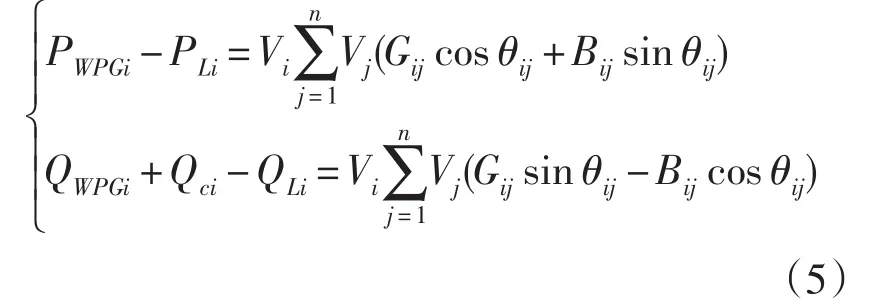
其中,PWPGi和QWPGi为节点i所接风力发电机发出的有功功率和无功功率;PLi和Qci为节点i处的有功负载及无功负载功率;Vi为节点i的电压幅值,Gij表示支路电导,Bij表示支路电纳,θij表示节点i与节点j之间的电压相角差。
(2)电压上下限约束为:
Vmin≤Vi≤Vmax
(3)可调变压器变比的上下限约束:
Kmin≤KX≤Kmax
(4)补偿点i的无功补偿容量约束:
0≤Qci≤Qimax
其中,Vmax和Vmin分别为节点i电压幅值的上下限;KX为可调变压器的变比,Kmax和Kmin分别为可调变压器变比的上下限。Qimax为节点i电容补偿量的最大值。
3 利用混合智能算法求解无功规划模型
3.1随机模拟技术
随机模拟技术又称蒙特卡洛模拟法(Monte Carlo Simulation, MCS),是一种广泛应用于随机问题分析的工具,尤其对于那种模型构成复杂、随机变量过多且具有相关性的问题,并常常用来检验其他概率潮流求解方法的求解精度其依据概率分布对随机变量进行抽样[7]。虽然模拟技术只能给出统计估计值而非精确计算值,且应用其求解问题时需要花费大量的计算时间,然而它确实是处理针对解析方法行不通的复杂问题(如机会约束规划模型)的可行工具,下面以式(9)所示的无功规划随机模型中的电压水平约束条件为例,给出利用MCS法检验随机规划模型中机会约束条件可行性的过程。
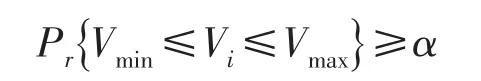
风速服从式(1)所示的Weibull分布,随机模拟算法如下:
设n′=0。
根据式(1)生成一个风速样本。
根据该风速样本计算风电场出力。
计算配电网潮流,如果对于系统每个节点都有Vmin≤Vi≤Vmax,则n′=n′+1。
重复步骤(2)~(4)n次
3.2混合智能算法
为求解基于机会约束规划的含分布式电源配电网无功规划问题,本文将粒子群寻优算法(Parti⁃cle Swarm Optimization, PSO)和支持向量机(Support Vector Machine, SVM)结合起来构造混合智能算法。考虑到在利用粒子群寻优算法对机会约束规划模型进行求解时,需对每一代种群的粒子进行适应度计算,从而进行种群更新。而在机会约束规划模型中,每个粒子的适应度都需要先在多种随机场景下来计算出目标值后才能得出,当随机场景数的设置较大时便涉及到大量的潮流计算,这直接导致随机规划模型的寻优求解效率低下。为了减少系统潮流计算次数以达到提高求解速度的目的,本文先根据随机模拟技术产生足够的训练样本,并采用支持向量机良好的拟合泛化能力对这些训练样本进行拟合,形成支持向量机回归拟合函数,并用它代替费时的潮流计算过程,即每个粒子的适应度值通过支持向量机拟合函数映射得出,从而使得混合智能算法在整个寻优过程中达到计算效率和求解精度的协调均衡。
因此,文本利用混合智能算法求解机会约束规划问题,算法流程如图1所示,其中每个粒子的目标值代表采用某种补偿方案后配网系统的网损值,而每个粒子的适应度则是采用该补偿方案后优化目标值f,并且在利用回归逼近函数检验更新例子的可行性时,如发现节点电压幅值的机会约束条件不符合,则对该粒子采用加惩罚项的方式处理。
4 算例分析
本文以IEEE33节点配电网系统为例,如图2所示,系统基础数据见文献[10],系统中有一台有载调压变压器,有5个分接口(UN±2×2.5%),单组补偿电容的容量为70 kvar,每一位置最多可安装10组补偿电容,且无功补偿电容装置的综合投资费用为70元/kvar,无功补偿装置使用年限为20年,贴现率取0.1,单位电能损耗费用取0.6元/kWh。节点6和节点31分别安装有一台异步风力发电机,其技术参数见文献[3],切入风速vci为5 m/s,切出风速vco为25 m/s,额定风速vr为 14 m/s,形状参数k为2.0,尺度参数c为7.5。
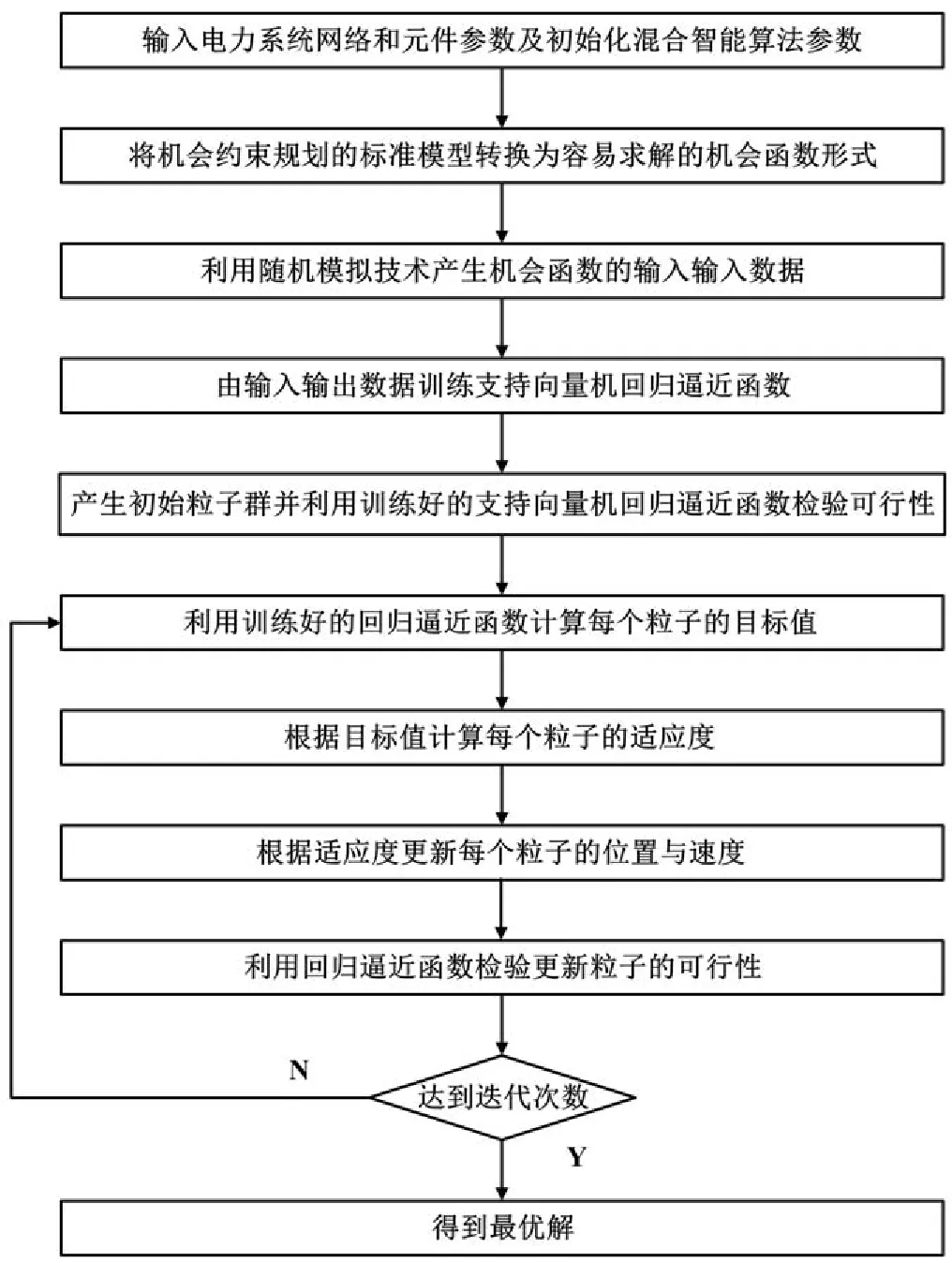
图1 混合智能算法流程图
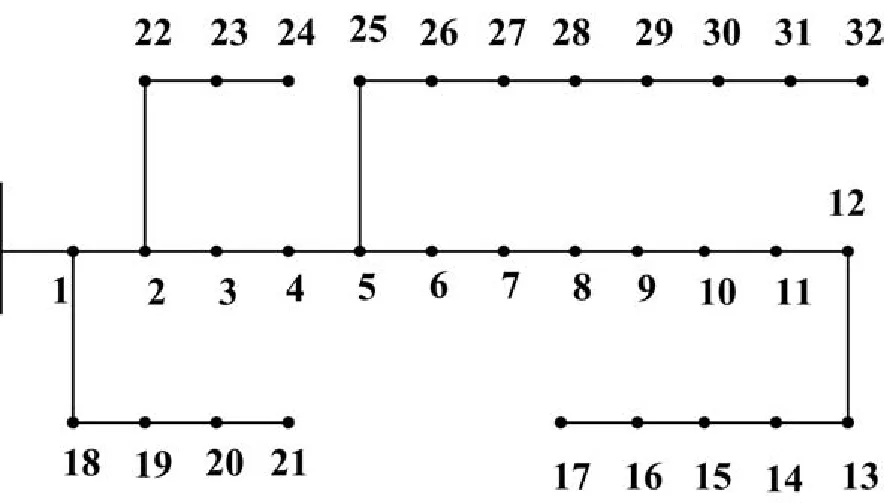
图2 IEEE33节点配网系统
为了检验混合智能算法的准确度及求解效率,本文先利用随机模拟与PSO算法相结合的随机机会约束规划算法求解33节点系统无功规划问题,即先随机模拟产生若干风速场景,对每一场景直接用PSO算法进行目标值寻优,其中随机风速样本取为200,目标函数置信水平β为0.9,电压约束条件置信水平α为0.99,节点电压标幺值的上下限约束为1.07和0.93,粒子群规模设为20,迭代次数为200。另外,根据图1所示的流程图,利用混合智能算法求解该相同问题时,产生训练样本数为1 250,然后分别利用BP神经网络和支持向量机建立回归拟合函数,其中支持向量机采用径向基核函数。三种算法的优化结果如表1所示,在优化结果中,括号前的数字表示电容补偿装置安装位置的节点号,括号内的数字为该位置投运的电容器组数。
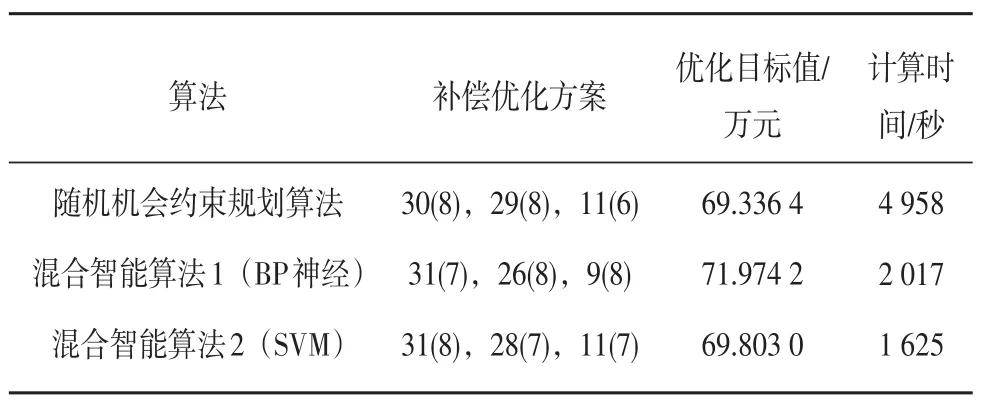
表1 无功规划结果对比
从表1可以看出,与传统的随机机会约束规划算法相比,利用混合智能算法求解得到的优化方案亦能达到较好的无功补偿效果,混合智能算法1(含BP)求解的最优目标值的相对误差为3.840%,而利用混合智能算法2(含SVM)的只为0.698%,因回归逼近函数造成的计算误差仍在容忍范围内。
并且,由于混合智能算法无需在整个粒子群寻优过程中,都对每一代种群的各粒子适应度进行精确计算,而是通过拟合函数进行适应度值估算,从而节约了大量潮流计算所耗费的时间。从表1可以看出,混合智能算法1计算耗时从4 958秒减少到2 017秒,而混合智能算法2则只需1 625秒,分别减少到原先的40.68%和32.78%。同时,通过两种混合智能算法的计算结果对比可看出,支持向量机较BP神经网络的拟合效果更佳,最后所得解的适应度更佳,并且支持向量机在训练拟合函数时较BP神经网络所耗费的时间更短。
更进一步,针对同一机会约束规划模型分别设置不同的目标函数置信水平和约束条件置信水平,并利用粒子群算法和支持向量机构造成的混合智能算法进行求解,求解结果如表2所示。
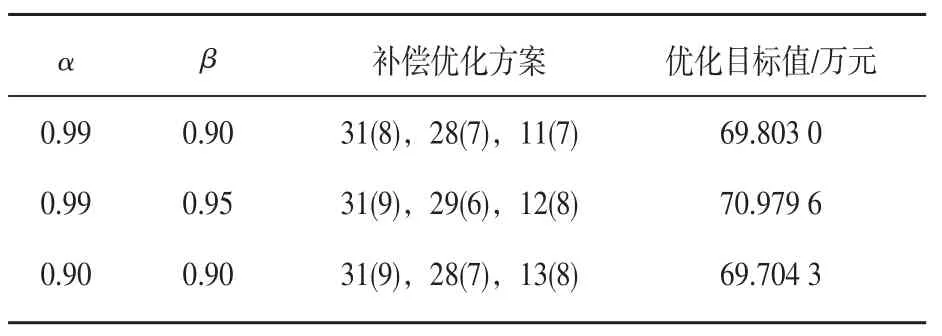
表2 不同置信水平下的优化结果
从表2可知,当保持模型中的电压水平约束条件置信水平不变而增加目标函数置信水平时,所得解的目标值将变大;另外,当保持模型中的目标函数置信水平不变而增加电压水平约束条件置信水平时,所得解到的目标值将变小,这表明此规划偏于冒险,较易造成电压越限。
在表3中,继续研究分布式电源不同接入情况下,利用混合智能算法2(含SVM)进行求解,可见随着接入点的增加,求解时间只是略有增加,依然具有较高的决策效率。
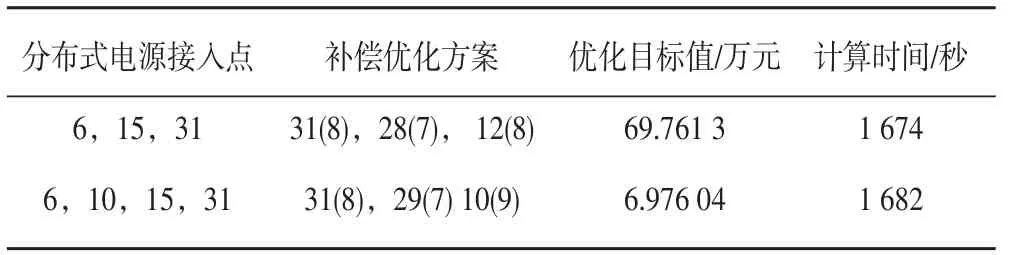
表3 分布式电源点增加后的优化结果
5 结论
本文建立了基于机会约束规划的含间歇性电源配电网无功规划的数学模型,利用随机模拟技术仿真表示风机各种出力状态,同时避免出现确定性约束条件造成优化结果过于保守。为了提高优化迭代速度,这里采用了混合智能算法进行求解,避免大量重复的潮流计算,并取得较好的计算精度,算例结果表明该方法有效可行,具有一定的工程应用价值。
参考文献:
[1]陈琳,钟金,倪以信,等.含分布式发电的配电网无功优化[J].电力系统自动化,2006,30(14):20-24.
[2]李晶,王素华,谷彩连.基于遗传算法的含分布式发电的配电网无功优化控制研究[J].电力系统保护与控制,2010,38(6):60-63.
[3]陈海焱,陈金富,段献忠.含风电机组的配网无功优化[J].中国电机工程学报,2008,28(7):40-45.
[4]刘学平,刘天琪,李兴源.含风电机组的配电网无功优化补偿[J].电力系统保护与控制,2010,38(20):130-135.
[5]Abouzahr I,Ramakumar R.An Approach to Assess the Performance of utility-interactive wind electric conver⁃sion systems[J]. IEEE Trans on Energy Conversion,1991,6(4):627-638.
[6]Charnes A,Cooper W W. Chance-constrained Program⁃ming[J]. Management Science,1959,6(1):73-79.
[7]Feijoo A E,Cidras J,Dornelas J L G. Wind Speed Simu⁃lation in Wind Farms for Steady-state Security Assess⁃ment of Electrical Power system[J]. IEEE Trans on En⁃ergy Conversion,1999,14(4):1582-1588.
[8]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.
[9]李爱国,覃征,鲍复民,等.粒子群优化算法[J].计算机工程与应用,2002,38(21):1-3.
[10]Baran M E,WU F F. Network reconfiguration in distri⁃bution systems for loss reduction and load balancing [J]. IEEE Trans on Power Delivery,1989,4(2):1401-1407. 33.
[11]朱勇,杨京燕,高领军,等.含异步风力发电机的配电网无功优化规划研究[J].电力系统保护与控制,2012,40(5):80-84.
(编辑:向飞)
Hybrid Intelligent Algorithm for Solving Reactive Power Planning Problem in Distribution System with Distributed Generation
ZHUO Ding-ming1,WANG Zeng-yu2
(1. Huizhou Power Sypply Bureau , Guangdong Power Grid Cooperation,Huizhou516000,China;2. Guangzhou Power Supply Co.,Ltd.,Guangzhou 510000,China)
Abstract:Based on the stochastic programming theory, the paper present a method to solve reactive power optimization problem in distribution system with distributed generation. In order to describe wind speed, random variables are led in, and the mathematical model which based on chance-constrained programming is built. Then the model is solved bythe hybrid intelligent algorithm combined with stochastic simulation, support vector machine, particle swarm optimization. Wind power generators were added to IEEE 33-bus system, and the modified test system study results show that the method has higher decision-making efficiency and calculation precision, and verify that the proposed model and method are reasonable and effective.
Key words:distributed generation;distribution system;reactive power planning;chance-constrained programming;hybrid intelligent algorithm
作者简介:第一卓定明,男,1989年生,广东梅州人,大学本科,助理工程师。研究领域:电力系统运行与控制。
收稿日期:2015-08-09
DOI:10. 3969 / j. issn. 1009-9492. 2015. 11. 030
中图分类号:TM727
文献标识码:A
文章编号:1009-9492 ( 2015 ) 11-0114-05
- 机电工程技术的其它文章
- TinyOS环境下交通信息采集自组网系统设计**国家自然科学基金资助项目(编号:50878088);广东省高等学校学科建设专项项目(编号:2013WYXM0133);广东省高等学校优秀青年教师培养计划资助项目(编号:Yq2013180)。
- 舵机加载系统及其伺服驱动器控制参数设置方法**航空科学基金资助项目(编号:20130863006)
- 基于海马号ROV富钴结壳的钻取技术研究**国家高技术研究发展计划(863计划)资助项目(编号:GZH201100307-04-01)
- 大摆锤驱动头动力学建模与仿真研究**国家质检总局科技计划项目(编号:2014QK255)
- 基于最小二乘法和递推最小二乘法的雷达伺服跟踪系统建模
- 基于ArtCAM的十二生肖浮雕加工研究**江苏省大学生实践创新计划项目(编号:201412808005Y)

