动边界约束梁在低速冲击下的动力响应

姜红艳，陈灿寿

(中国人民解放军理工大学国防工程学院，江苏 南京 210007)

目前，在各种重要的建筑物和构筑物设计中对低速冲击事故作用需要给予极大的关注。国内外对钢筋混凝土梁在低速冲击作用下的研究工作中进行了大量的实验研究［1］，但至今尚未对实验研究结果进行系统分析。文献［2］只研究了单个钢筋混凝土梁构件在低速冲击下的局部与整体变形和破坏特征，通过简化计算模型，得出了钢筋混凝土梁在低速冲击下的计算公式，但不能满足实际工程中一些梁系结构的动力计算。文献［3］研究了柔性动边界梁在横向撞击下的动力响应，说明了低速撞击条件下柔性支承对撞击力和横向位移的影响，但其只考虑了弹性阶段，未考虑塑性阶段的情况。文献［4］研究了梁系结构在低速冲击下的动力计算方法、对受力梁和支承梁处在不同应变阶段的判别条件，推导了相应的冲击力和梁横向位移的计算公式，但在实际工程中，梁系结构通常下部支承的刚度远大于上部梁的刚度，因此，进行动力计算时，可只研究下部支承梁在弹性阶段工作，上部构件既可在弹性阶段工作又可在塑性阶段工作的情况。

本文建立了动边界约束梁的力学模型。支承构件的作用可以用带集中质量的弹性支承实现。受力构件考虑弹性和塑形两种情况。利用了一种新的表达振型的方法，并利用冲击局部区域的接触力与嵌入深度的关系式来研究结构的响应，通过不同大小的约束条件下冲击力、横向位移的对比，来分析说明动边界对结构响应的影响。

1 模型及计算方法

如图1所示，一两端具有弹性约束的梁受横向冲击，冲击点为梁中点，考虑两端支承条件对称，竖向弹性支承刚度分别为 k0、k1，k0=k1，梁端刚性质量块为 m0、m1，m0=m1。

图1 两端受弹性约束梁的冲击模型

1.1 冲击力的确定

由于低速冲击下接触的持续时间较长，接触区的变形过程可以采用准静态的接触理论确定。

根据接触理论，圆球初始撞击速度不大，表征接触力F和侵彻深度α的关系为

式中，Kc为接触刚度，取决于材料的特性和接触双方的几何尺寸关系。

式中:R为圆球的半径;μ为泊松比;E为弹性模量。

1.2 位移表达式的确立

梁上任一点处的位移可表示为

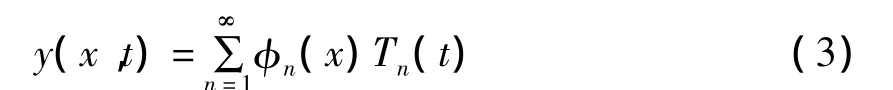
式中:Tn(t)为待求的时间函数;φn(x)为梁的振型函数［5］，可表示为

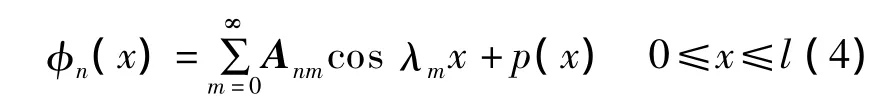
对式(4)逐项求导，可得到:

这样多项式函数p(x)可以很容易得到

梁在端点处的边界条件公式为:

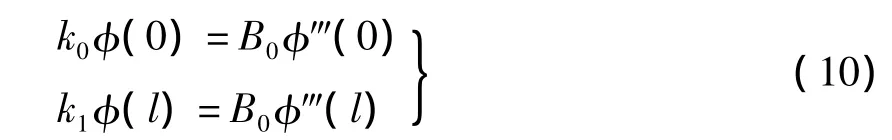
式中:B0为梁的抗弯刚度，B0=EI0;I0为冲击区域外的截面惯性矩，I0=bh3/12。

结合式(4)、(7)和(11)，最后标准振型可表达为

式(4)中傅里叶级数的扩展系数通过求解一个矩阵的特征向量［5］就可以得到。

式中:ωn为频率;ρD= ρA/B0，ρ为质量密度，A 为梁横截面的面积。

这样，对于任意变化的竖向弹性刚度可以求出梁的位移表达式。

1.3 准弹性阶段

采用拉格朗日法建立梁在冲击作用下的动力方程。动能、位能和外力功的表达式如下:

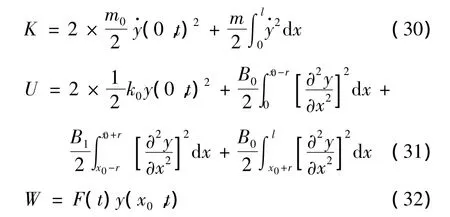
式(30)～(32)中:m为梁的单位长度质量;r为撞击区域半径，一般情况下取冲击体长度尺寸的为冲击区域内梁截面弯曲刚度，其中B考1虑了由于冲击体侵入到梁内一定深度而造成梁刚度的降低;x0表示接触面轴线通过的截面坐标。

冲击体的运动方程为

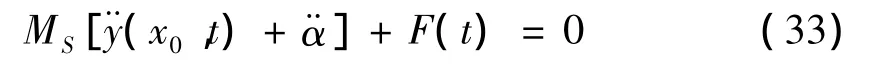
式中，MS为冲击体的质量。

将式(3)代入式(29)～(31)，再代入拉格朗日方程

加上冲击体运动方程式(33)，取接触定律公式(1)，得到运动方程:

可以看出，δi反映冲击的局部损伤对梁整体响应的影响。在低速冲击情况下，冲击体侵入到钢筋混凝土梁内的深度很小，有时可以忽略不计。此时的运动方程只须令δi=0即可。

式(35)在准弹性阶段冲击体与梁之间的接触未结束及接触力未超过极限接触力的情况下是成立的。

如果在t0时冲击体与梁的接触中止，则在t＞t0时只须令α=0，并删掉最后一个方程式即得到动力方程组。

1.4 塑性阶段

如果承受冲击荷载的钢筋混凝土梁截面受拉钢筋中的应力达到动力屈服强度Mu，d，就认为进入塑性阶段，在塑性截面会出现塑性铰。确定梁的动力屈服弯矩时，必须考虑变形速率对钢筋混凝土材料的动力强化作用。假定在ts时受力梁进入塑性阶段，塑性铰出现的位置为x0。

进入塑性阶段后，梁的位移则改为

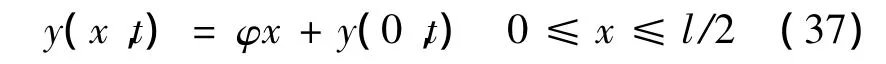
式中，y(0，t)表示两端弹性支承引起的位移，此时动能、位能和接触力做功的表达式为

将式(38)～(40)代入拉格朗日方程并进行变换，再加上冲击体的运动方程

按接触定律的形式，得到可求解的方程组:

式(42)的初始条件由开始进入塑性阶段时刻ts的连续性条件确定，假如从塑性阶段开始时刻为计算时间起点，则当t=0时，有:

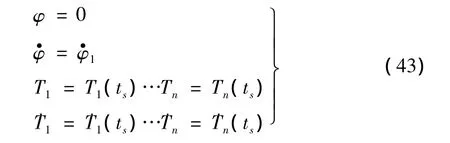
当冲击体与梁之间的接触中止，就要研究梁的自由振动，需令式(42)中α(t)=0，并删除最后一个方程即得到其自由运动方程。

2 算例

梁长l=6 m，梁截面尺寸b×h=200 mm ×600 mm，抗弯刚度B0=EI0=1.08×108N，单位长度梁的密度m=250 kg/m，接触刚度Kc=1.7×1010N/m1．5，质量ms=2 600 kg，从高度0.61 m 掉下垂直撞击梁中部。对于支座参数，定义相对刚度系数

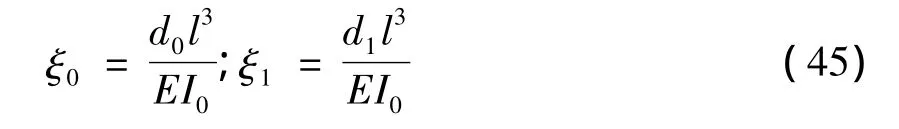
计算时取前3阶振型，m=5，不考虑轴力和轴向位移的影响，利用数值方法，研究不同大小的弹性支承刚度对梁动力响应的影响。取ξ1=ξ2=ξ，m1=m2=0，分别考虑ξ为0.02、20、200的3种情况。

图2为简支梁前3阶振型，分别用式(4)(计算时取k0=k1=∞)与传统的简支梁公式φn(x)=sin(nπx/l)比较，从图中可以看出，2种方法得到的图形基本重合，误差很小，说明式(4)较为可靠。

图2 简支梁振型

图3 为低速冲击荷载作用下不同竖向弹性约束刚度时梁的中点位移时程曲线，该位移是指由弯曲变形引起的挠度，不包含支座引起的刚性位移。可以看出，不同支承刚度条件下，支承刚度越大，横向位移也越大，这是由于支座竖向位移所引起的附加惯性力的影响，但当支承刚度很高时，这种效应在一定程度上消失了。

图4为冲击力的时程曲线，从中可以看出，冲击力受弹性支承的影响较大，两端支承刚度越大，撞击力的峰值越大。

3 结论

1)一种新的方法可以求解不同边界条件的梁的振型，与传统的三角和双曲函数相比，求解过程简单。

2)在梁系结构的受力过程中，由于支承构件会产生变形，因此梁系结构的动力计算可归结为动支座问题。

3)低速冲击时，支承刚度对撞击力和支座的横向位移都有显著影响。

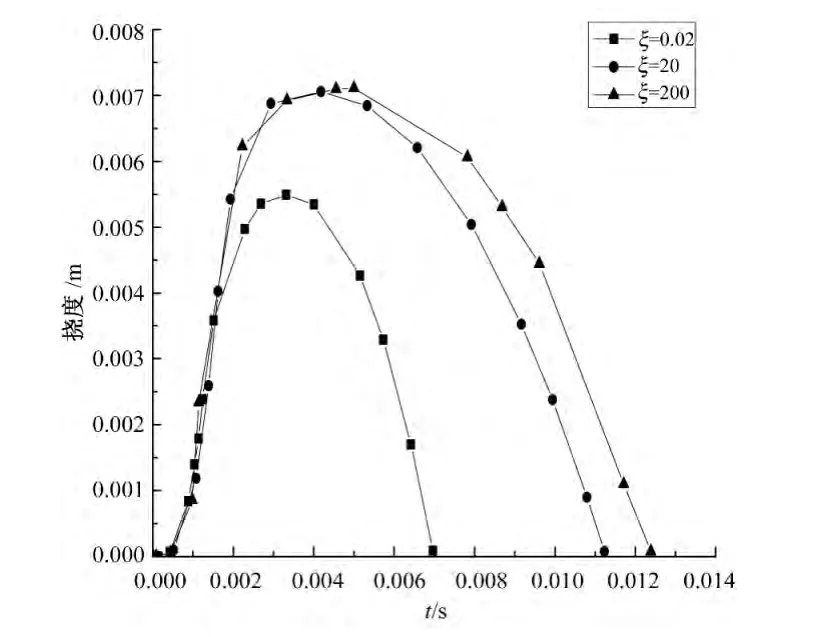
图3 受冲击处梁相对于支座的横向位移

图4 不同支承的撞击力

［1］Попов Н Н，Расторгуев Б С，Забегаев А В．Расчетконструкций надинамическиеи специальныенагрузки［M］．Москва:Высшая школа，1992:241 －245．

［2］王明洋，王德荣，宋春明．钢筋混凝土梁在低速冲击下的计算方法［J］．兵工学报，2006(5):399 －405．

［3］宋春明，王明洋，唐正国．柔性动边界梁在横向撞击下的动力响应［J］．解放军理工大学学报(自然科学版)，2008，9(2):151－155．

［4］王德荣，李杰，宋春明，等．梁系结构在低速冲击下的计算方法［J］．兵工学报，2007(3):309－314．

［5］LI W L．Free vibrations of beams with general boundary conditions［J］．Journal of Sound and Vibration，2000，237(4):709 －725．