太阳同步轨道立方星任务轨道演化分析
雷博持 李明涛
1.中国空间技术研究院西安分院,西安710100
2.中国科学院空间科学与应用研究中心,北京100190
立方星这一概念最早由美国加州理工大学和斯坦福大学在1999年提出,立方星是标准化的微小卫星,尺寸10 cm×10 cm×10 cm,质量约1 kg,为一个基本单元1 U。以此为基础可以有2 U、3 U等立方星。立方星具有很多特点,不仅成本低,开发时间也较短,易于实现标准化、模块化,易于技术更新[1-2]。
近年来,利用多卫星系统的空间任务越来越多,借助标准化的微小卫星来实现分布式空间系统极具发展前景。分布式空间任务的出现,拓展了立方星在科学领域的应用。目前已有越来越多的立方星被送上太空。国外的立方星应用主要分为3个方面:以空间科学和教学为核心目标,如荷兰代尔夫特理工大学的 Delfi-c3;以载荷任务为目标,如 QuakeSat搭载了地震电磁探测载荷;也有以新技术验证为目标的立方星任务,如加拿大的先进纳星太空实验室CANX卫星系列[3]。国内很多高校及科研机构也在积极开展立方星的相关研究。
体积小、重量轻的自身特点决定了立方星大多没有在轨机动能力,考虑无主动控制时立方星轨道的自然演化就成为一个重要研究方向。太阳同步轨道(SSO)具有星上光照条件好、过同一纬度的当地时间相同等特点,已被广泛应用于各种空间任务。因此,本文选取了SSO立方星任务进行轨道演化研究,考虑地球非球形引力项J2和大气阻力摄动的影响,以平均半长轴随时间的变化作为摄动效应的指标。以轨道分析软件为仿真平台,先进行了摄动力简化以及立方星面质比对轨道演化的影响分析,以确立数值仿真的前提条件;接着研究了轨道高度、太阳活动指数和大气模型这3个方面对SSO立方星轨道演化的影响。最终得出结论。
1 卫星轨道动力学模型
1.1 坐标系定义
研究地球非球形摄动及大气阻力摄动对轨道演化的影响时,涉及到地心惯性坐标系和地心地固坐标系,如图1所示。Oxiyizi(标记为 Si)为地心惯性坐标系,Oxeyeze(标记为Se)为地心地固坐标系,α为Greenwich赤经。
地心惯性坐标系Si:坐标系原点在地心,Z轴垂直于地球赤道平面;XY轴在地球赤道平面内,X轴指向春分点位置;Y轴满足右手螺旋定则。动力学方程一般建立在惯性坐标系中。
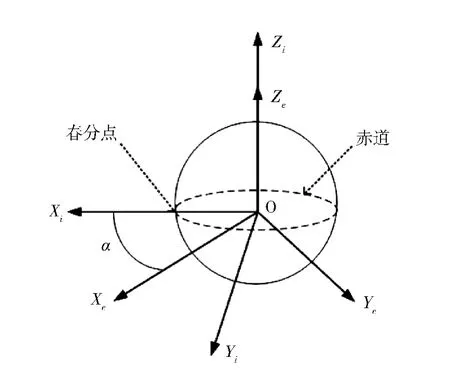
图1 地心惯性坐标系和地心地固坐标系
地心地固坐标系Se:坐标系原点在地心,Z轴垂直于地球赤道平面;XY轴在地球赤道平面内,X轴指向 Greenwich子午圈与赤道交点;Y轴满足右手螺旋定则。地球非球形摄动一般在地心地固坐标系中表示。
1.2 动力学模型
在惯性坐标系下,卫星动力学模型可用式(1)表示。
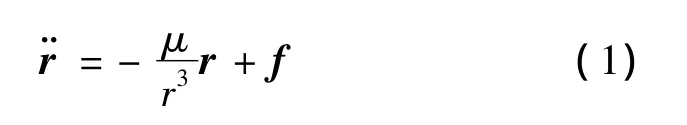
式中:r为地心距矢量,μ是地心引力常数,r为地心距大小,f为地球中心引力之外的所有摄动力的合力和包括地球非球形引力、大气阻力、太阳光压、第三体引力摄动等。
将式(1)在惯性坐标系下展开并进行积分,可以得到任意时刻卫星在惯性坐标系下的运动状态。
2 地球非球形摄动和大气阻力摄动分析
对于低轨道来说,卫星所受到的摄动力主要是地球非球形引力摄动、大气阻力摄动、太阳光压摄动以及第三体引力摄动。设f0表示地球中心引力加速度的大小,fe表示其他类型的摄动加速度的大小。与地球中心引力相比,用η=fe/f0来表征各摄动力的量级估算值,如表1所示。其中大气阻力摄动与第三体引力摄动力均为10-7,但第三体引力摄动要小于大气阻力摄动,且轨道高度越低,大气阻力摄动的作用越大。由此可见,对于低轨卫星,J2摄动最重要,其次是大气阻力摄动[4]。我们可以对摄动力进行简化,仅考虑J2摄动和大气阻力摄动的影响。

表1 各种摄动力的量级
2.1 J2项摄动
在两体问题中,认为地球是一个均匀球体,卫星运行在地球中心引力场中。但实际上地球形状是不规则性的,质量分布也不均匀,常将地球引力势函数表示成如下形式:
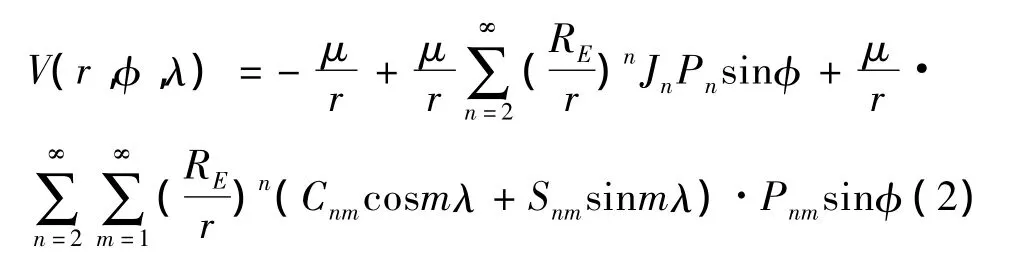
式中:r为到观测点的地心距,φ为地心经度,λ为地心纬度,RE是赤道半径,Pn,Pnm是正则勒让德多项式,Cnm,Snm,Jn为引力场系数。
对引力势函数(2)求梯度,可以得到卫星在地心地固坐标系下的加速度,再通过坐标转换转到地心惯性坐标系,即可以得到惯性系下卫星的动力学方程。J2项的影响要比其他项大100倍以上,通常仅考虑J2项摄动的影响。
2.2 大气阻力摄动
大气阻力是非保守力,在其影响下,卫星轨道会发生衰减。大气阻力摄动对卫星所产生的加速度如下式:
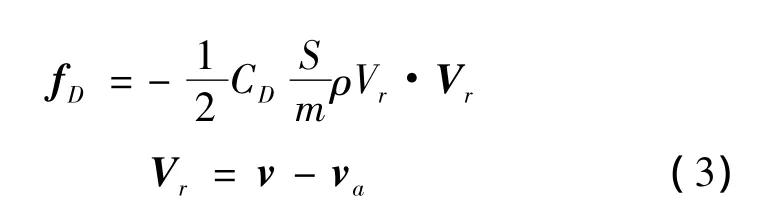
式中:fD为大气阻力摄动加速度,Vr为卫星相对大气的相对速度矢量,Vr为卫星相对大气的相对速度的大小,v和va分别为卫星和大气相对地心惯性坐标系的速度矢量,ρ为大气密度,CD为阻力系数。S/m为面质比参数。
另外,分析大气阻力摄动时,必须考虑以下几方面因素:
1)CD,阻力系数一般与卫星表面材料有关,常取2.2;
2)S/m,面质比与有效迎风面积有关,即要考虑卫星姿态和形状,通常选用一个等效面质比来进行计算;
3)va,大气转速比较复杂,约为地球自转速度的0.8~1.4倍,通常认为两者相等;
4)ρ,大气密度是极其复杂的问题,与轨道高度、温度、太阳活动指数等密切相关,变化幅值非常大。已有的大气模型也很多,如指数模型,Jacchia 77模型、NRLMSISE2000模型等,其中 NRLMSISE2000大气模型是由美国海军研究实验室于2000年在MSISE-90模型的基础上发展而出,是最新更新的一个大气模型,与其他模型相比具有很多优势[5]。
2.3 J2项摄动和大气摄动影响下的卫星运动方程
基于2.1节和2.2节的分析,可以得到同时考虑J2项摄动和大气阻力摄动时,卫星在惯性系下的运动方程如下式:
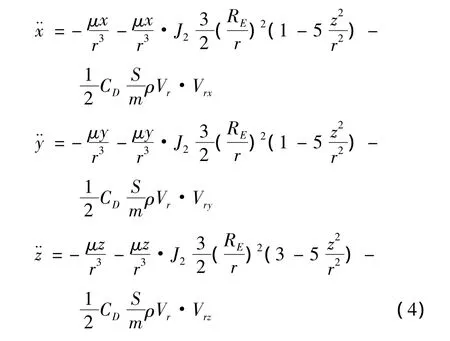
给定卫星初始时刻的运动状态后,对式(4)进行数值积分,就可以得到在J2摄动和大气阻力摄动同时影响下,卫星轨道的演化进程[6]。
3 仿真分析
在轨道仿真软件STK中建立一个SSO轨道,将其偏心率、近地点幅角、真近点角设置为0,降交点地方时设置为18时。改变轨道高度、设定轨道预报器就可以得到满足文章要求的各种仿真条件。
首先分析了面质比对轨道演化的影响并进行仿真,以确立出基本的仿真初始条件。然后分别仿真分析了轨道高度、太阳活动指数以及不同大气模型对轨道演化的影响。由于瞬时轨道根数波动性比较大,无法表现卫星受摄运动的本质,文中用平均轨道根数下的半长轴作为摄动效应的衡量指标。
3.1 面质比的选定
由2.2节可知,在研究大气阻力摄动时,必须考虑卫星面质比的影响,本文研究对象是1 U立方星,边长为10 cm,质量约为1 kg,所以面质比的变化范围为:0.01~0.014。在STK中,考虑J2项和大气模型为 NRLMSISE2000时的大气摄动,在0.01~0.014之间以0.0005为步长改变面质比,仿真不同面质比对500km SSO立方星轨道演化的影响,利用所得9个数据点绘图,如图2所示。横坐标是面质比,纵坐标代表半长轴的衰减量。

图2 SSO立方星轨道演化与面质比的关系
从图2可以看出,面质比对轨道演化有很大影响,仿真分析时必须合理选择面质比;轨道演化情况大致与面质比成线性关系。文中以下章节的仿真中,面质比默认选定为0.01m2/kg。
3.2 轨道高度对轨道演化的影响
以NRLMSISE2000大气模型为例,研究大气对不同高度SSO立方星轨道演化的影响,仿真时间180d。NRLMSISE2000大气模型中,太阳活动指数F10.7按默认值为150。在300~700km范围内以100km为步长改变轨道高度,所得到的半长轴演化情况汇总如表2所示,从仿真结果中选出400km,600km高度轨道的演化图,分别如图3和4所示。由此可以得到180d内轨道衰减的情况。图3中,在大气阻力作用下,145d左右时轨道高度直线下降,卫星陨落,寿命终止。图4中,仿真结束时,轨道衰减了约3.6km。
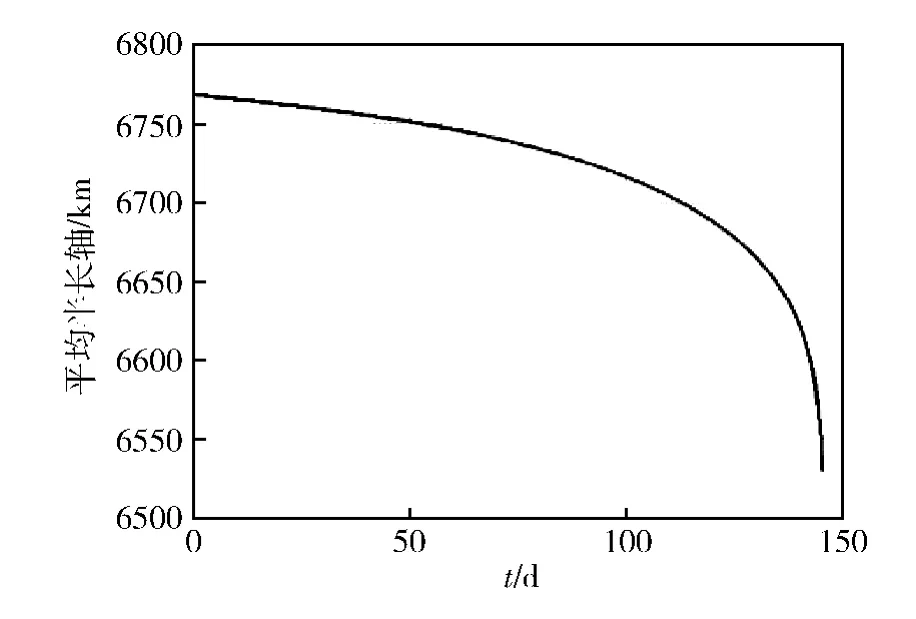
图3 400km SSO立方星轨道演化
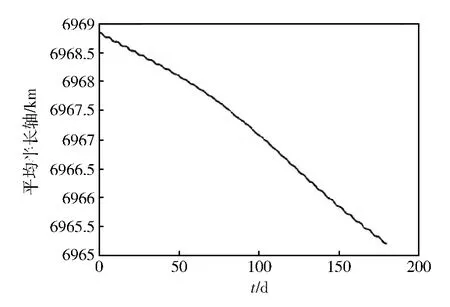
图4 600km SSO立方星轨道演化

表2 轨道高度对轨道演化的影响(F10.7=150)
从表2可以看出:1)大气阻力摄动对轨道演化(半长轴衰减)影响很大,且轨道高度越低影响越明显;2)高度300km的轨道,寿命约23d。高度为400km时,轨道寿命约150d。而对于500km高的轨道,半长轴衰减了16km。由此可见,轨道的演化情况与轨道高度间存在非线性关系。
3.3 太阳活动对轨道演化的影响
太阳活动指数F10.7指太阳发出的波长为10.7cm的电磁辐射强度,其变化没有严格规律,一般由观测得到。
F10.7的长期预测具有不准确性,以2015年6月1日为例,STK轨道分析软件8.1.1根据2007年5月24日的观测数据,预测的F10.7参数为77.7;STK轨道分析软件9.2.1根据2009年4月29日的观测数据,预测的F10.7参数为101.4;NOAA根据2012年11月26日的观测数据,预测的 F10.7参数为117.2[7]。由此可见,实现以年为单位的 F10.7参数预报,误差很大。应该采用尽可能新的预测数据。
由于F10.7的不确定性,导致大气密度相应地也存在不确定性。因此,在考虑大气阻力摄动时,有必要研究太阳活动指数F10.7对轨道演化的影响。
根据太阳活动指数随年份变化的趋势,选择太阳活动高、低年时的 F10.7参数分别为 200和70[8]。然后分别分析太阳活动高、低年时,大气对不同高度SSO演化情况的影响。
当轨道高度为300~1000km时,可以分别得到太阳活动高、低年时轨道半长轴的演化情况,汇总如表3。

表3 F10.7参数对轨道演化的影响
选取太阳活动低、高年时500km SSO的演化情况,分别如图5和6所示。由图5和6可以看出,对于500km的SSO轨道,太阳活动低、高年时的轨道演化情况差距很大,仿真结束时,轨道半长轴分别衰减了2km和37km。
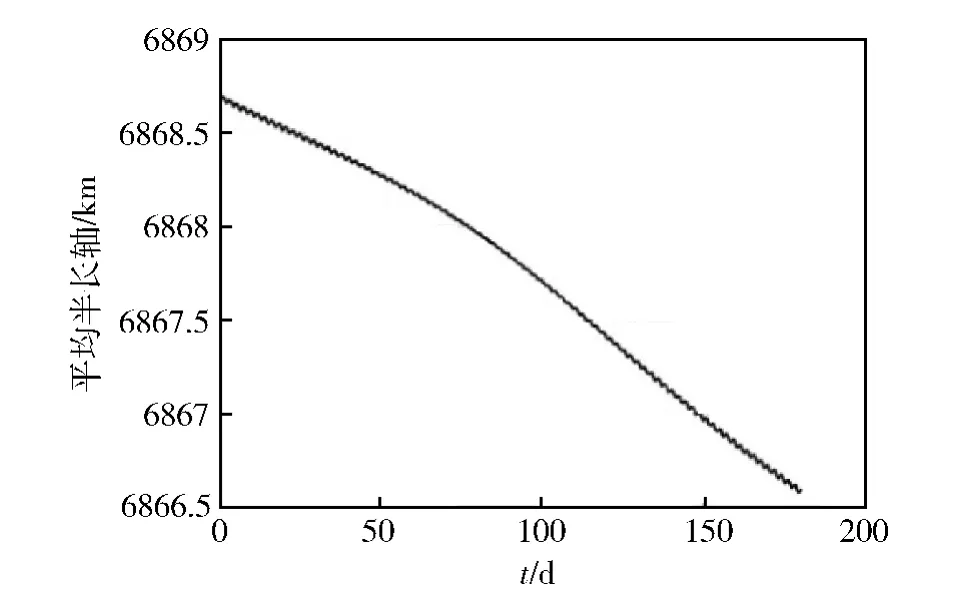
图5 太阳活动低年时的轨道演化情况
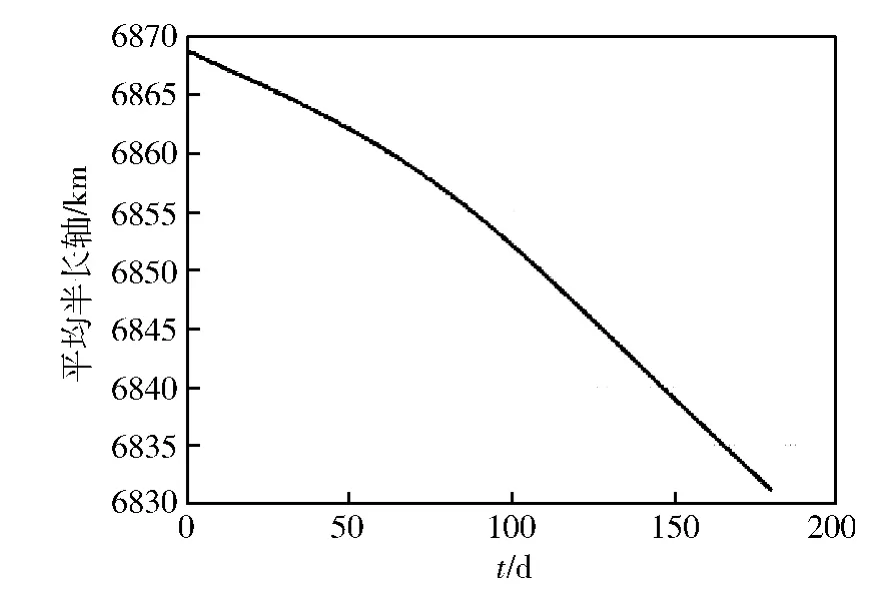
图6 太阳活动高年时的轨道演化
从表3可以看出,对于同样高度的SSO立方星,太阳活动高、低年时的轨道演化差别很大;太阳活动指数越高,可以忽略大气阻力摄动的最低轨道高度也越高。一般认为180天内半长轴衰减量小于1 km时,就可以忽略大气阻力的影响。
下面以500 km SSO轨道为例,研究轨道高度不变时,半长轴衰减量随F10.7的变化,以得到F10.7对轨道衰减的影响曲线图。在70~200之间改变F10.7,步长取10。利用所得数据点绘图,如图7所示。由图7可知,对同一高度的轨道,太阳活动指数越高,轨道衰减就越快;轨道衰减量与F10.7呈现出非线性关系。
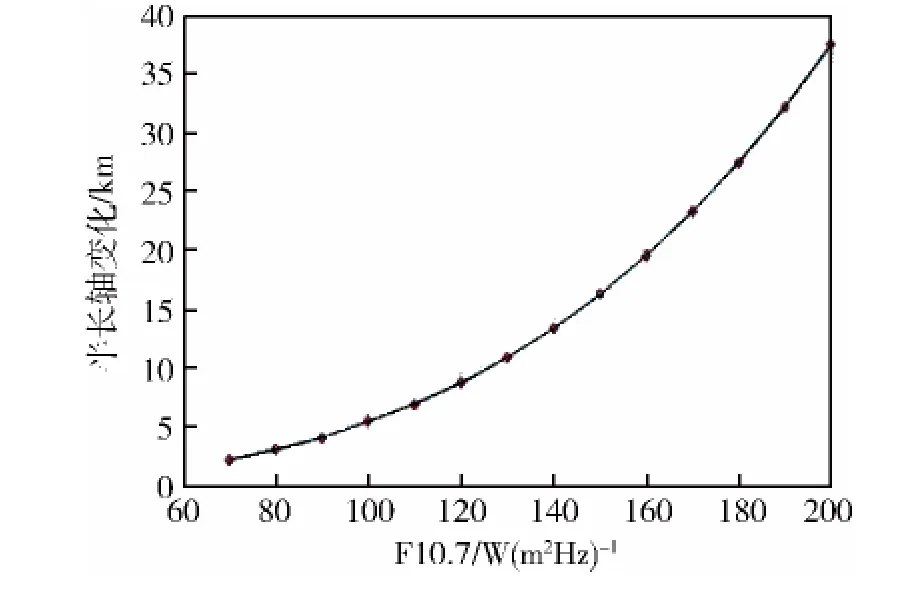
图7 半长轴衰减量与F10.7之间的关系
3.4 大气模型对轨道演化的影响
由2.2节可知,分析大气阻力摄动时,必须考虑大气模型的影响。目前已经有多个大气模型,然而这些模型的统计精度只有15% 左右。
以高度为500 km的典型 SSO轨道为例,选用不同的大气模型,对轨道半长轴随时间的演化进行分析,仿真初始条件与上文相同。分别选用了8个大气模型:Cira 72模型,Exponential-Earth模型,Harris-Priester模型,Jacchia-Roberts模型,Jacchia-1971模型,MSIS 1986模型,US Standard Atmosphere模型以及NRLMSISE 2000模型。各模型中涉及到太阳活动指数F10.7的,都按照默认设置为150。
对于指数大气模型,仿真时要输入参考高度和标准高度,按式(5)计算[9]。

式中:H为标准高度,H0为参考高度,r为卫星质心的地心距。μ≈0.1(常取μ<0.2),H0=37.4 km,r0=H0+6371 km。因此,对于500 km轨道,计算可得参考高度是37.4 km,标准高度是60.887 km。
分别设置不同的轨道预报器,以改变大气模型。仿真180d,得到不同大气模型下半长轴的演化情况,如表4所示。
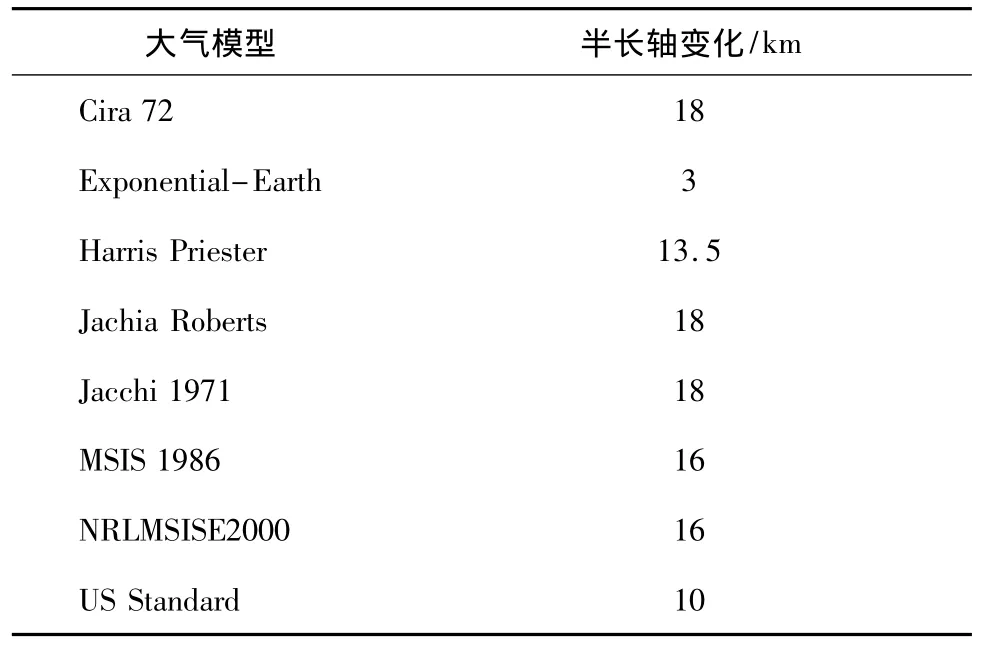
表4 不同大气模型对轨道演化的影响(180d)
从表4可以看出,在不同大气模型的影响下,轨道演化情况不尽相同,大多数模型的影响效果的量级约为16 km;与其他模型相比,指数大气模型影响下的半长轴演化情况悬殊,反映出指数大气模型的精度不够高。
4 结论
立方星是近年来纳卫星领域的研究热点。本文对SSO立方星任务的轨道演化情况进行了仿真分析,得出如下结论:
1)对于300~700 km轨道高度的立方体卫星,大气阻力摄动对轨道寿命有明显影响,导致半长轴不断衰减,轨道越低影响越大,且影响结果与轨道寿命成非线性关系;
2)太阳活动对大气阻力摄动有显著影响,太阳活动高、低年时的轨道演化情况差距很大。在分析大气阻力摄动时,必须考虑F10.7参数的影响,且影响效果与F10.7间存在非线性关系;
3)选取不同大气模型时,轨道演化情况不完全相同。大多数大气模型之间的轨道演化情况差距并不大,指数模型与其他模型相比存在一定偏差。
综上所述,考虑轨道高度、太阳活动及大气模型的耦合影响,对单颗SSO立方星任务轨道的选定具有参考意义。另外,单星的轨道演化是研究立方星编队的基础,星间无碰撞的安全飞行高度的确定、星间相对距离的演化情况及编队构形控制方法可以作为下一步的研究方向。
[1] Sundaramoorthy P P,Gill E,Verhoeven C J M,Bouwmeester J.Two CubeSats with Micro-Propulsion in the QB50 Satellite Network[C]//Proceeding of the 24th Annual AIAA/USU Conference on Small Satellites,SC10-III-3.Washington:AIAA,2010:1-5.
[2] 林来兴.立方体星的技术发展和应用前景[J].航天器工程,2013,23(3):90-98.(Lin Laixing.Technology development and application prospects of cubeSat[J].Spacecraft Engineering,2013,22(3):90-97.)
[3] 李军予,伍保峰,张晓敏.立方体纳卫星的发展及其启示[J].航天器工程,2012,21(3):80-87.(Li Junyu,Wu Baofeng,Zhang Xiaomin.Development of cubeSat and its enlightenment[J].Spacecraft Engineering,2012,21(3):80-87.)
[4] 王融,熊智,等.基于受摄轨道模型的小卫星轨道摄动分析研究[J].航天控制,2007,25(3):66-70.(Wang Rong,Xiong Zhi,et al.Analysis and research of micro satellite orbit perturbation based on the perturbative orbit model[J].Aerospace Control,2007,25(3):66-70.)
[5] 卢明,李智,陈冒银.NRLMSISE-00大气模型的分析和验证[J].装备指挥技术学院学报,2010,21(4):58-61.(Lu Ming,Li Zhi,Chen Maoyin.Analysis and verification of the NRLMSISE-00 atmospheric model[J].Journal of the Academy of Equipment Command &Technology,2010,21(4):58-61.)
[6] 黄勇,李小将,王志恒,李兆铭.J2项和大气阻力摄动作用下卫星编队构型的演化分析[J].航天控制,2013,31(3):62-66.(Huang Yong,Li Xiaojiang,Wang Zhiheng,Li Zhaoming.The evolvement analysis of satellite formation under J2 term and atmosphere drag perturbation[J].Aerospace Control ,2013,31(3):62-66.)
[7] NOAA.Solar Cycle F10.7 cm Radio Flux Progression[EB/OL].[2013-05-20]http://www.noaa.gov.
[8] 刘暾,赵钧.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社,2003:253-255.(Liu Tun,Zhao Jun.Dynamics of Spacecraft[M].Harbin:Press of Harbin Institute Technology,2003.)
[9] 刘林.航天器轨道理论[M].北京:国防工业出版社,2000.(Liu Ling.Orbit Theory of Spacecraft[M].Beijing:Defense Industry Press,2000.)

