基于BP神经网络的色纺纱配色
沈加加,周 翔,屠天民
(1.东华大学化学化工与生物工程学院,上海 201620;2.嘉兴学院材料与纺织工程学院,浙江 嘉兴 314001)
色纺纱的配色不同于纺织品的染色配色,需要通过选择不同颜色的已染色纤维以及调节它们间的组合比例,由梳棉、并条、粗纱、细纱等纺纱工序来生产目标色,因此该配色过程除与配色理论有关外,受纺纱工艺的影响也较大。以往的色纺纱配色研究主要围绕 Kubelka-Munk 理论[1]、Stearns-Noechel公式[2]和 Pineo-Friele 模型[3-4]及其参数[5-6]和算法优化[7-9]进行,但这些模型存在不足,模型推导过程中使用了众多假设条件,往往这些假设条件都与实际情况不符,导致在生产应用时准确率不高。
人工神经网络是一种类似大脑神经突触连接结构进行分布式并行信息处理的算法模型,具有强大的数据处理能力和非线性映射能力。在纺织品的染色配色和涂料配色方面已有不少成功的应用研究基础,1991年,Stephen Westland等[10]在对传统配色方法进行分析的基础上提出了一种多层感知神经网络的模型,用LAB和LCH值作为输入值验证了神经网络方法的可行性。文献[11]将Kubelka-Munk法与神经网络法加以定量地对比分析后,认为最有效的方法可能是将二者结合。文献[12]用18种颜料作了相关实验,与目测结果相对照,并深入进行了部分相关参数设置的探讨,进一步肯定了神经网络法用于配色的可行性。在色纺纱配色上,意大利学者Furferi[13]将神经网络与经典模型进行比对,神经网络配色得到的平均预测色差小于0.24,认为比经典模型更优,但文章没有提及该神经网络的泛化能力,泛化能力是评估模型是否具备实用价值的关键。
本文研究采用BP神经网络建立色纺纱反射率与配方之间的非线性映射模型,探讨应用神经网络进行色纺纱配色的可行性,为色纺纱辅助配色技术的发展提供一些理论基础。
1 色纺纱BP神经网络配色模型构建
理论上,BP神经网络可以逼近任意连续函数,具有很强的非线性映射能力,而且各层间的学习参数可以根据具体情况设定,因此适宜在色纺纱这种复杂配色的应用。
采用简单的3层前馈网络,输入层由色纺纱样本的反射率Rλ组成,波长λ范围为400~700 nm,间隔10 nm,构成 31 维输入向量 P=[R400,R410,…,R700]T;输出层为色纺纱样本的配方 Y,Y=[yα1,yα2,…,yαm]T,表示该配方中的 m 个组成单色纤维(α1,α2,…,αm)分别对应的配方比例 y 值,因此输出层的神经元个数即为组成单色的个数m。
选用最简单的单隐含层,输入输出关系由以下公式给出:
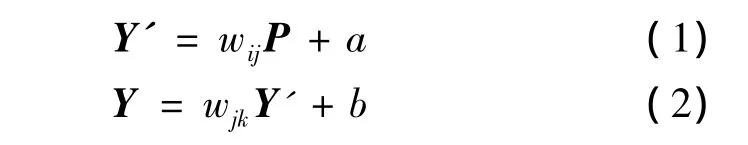
式中:P为输入数据Rλ经初始化后的神经元输入;wij、wjk是初始化输入层、隐含层和输出层神经元之间的连接权值;a为初始化隐含层阈值;b为输出层阈值。根据式(1),P在隐含层传递函数f0的作用下产生该层的输出Y',根据式(2),Y'在输出层传递函数f1的作用下产生该层的输出Y,整个色纺纱神经网络配色模型的向量关系如图1所示。

图1 色纺纱神经网络配色模型向量图Fig.1 Vector diagram of neural network recipe prediction model of melange yarn
2 实验部分
2.1 训练样本的制备
应用BP神经网络进行色纺纱的配色实验,需要定义训练样本,验证样本和测试样本。本文选用了3对颜色组合,分别为黑-白(用α1-α2表示)、红-绿(用α3-α4表示)、黄 -蓝(用 α5-α6表示),每对组合按 10∶90,20∶80,…,90∶10 比例两两混色形成27个棉混色样本,每个样本总质量为10g,分别从每对颜色组合中随机抽取1个样本共计3个样本作为验证样本,剩余24个样本作为训练样本。另外根据这6个颜色设计了6个具有代表性的样本作为测试样本,测试样本的实际配方如表1所示。
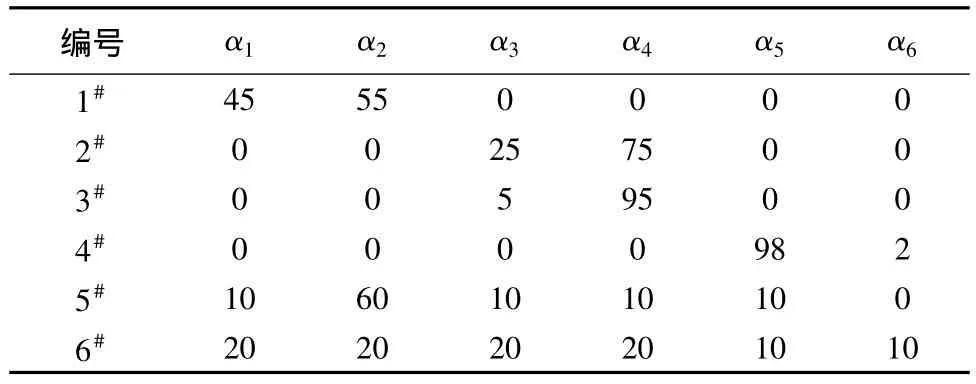
表1 测试样本的配方Tab 1 Recipes of test sample %
因此,构成的样本矩阵组成如下:
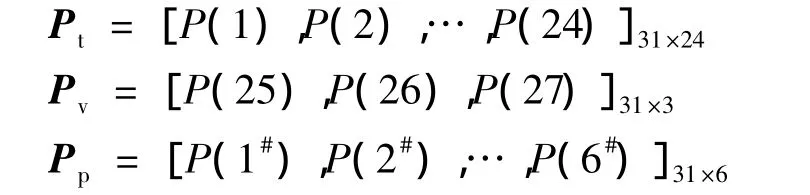
式中:Pt表示训练数据;Pv表示验证数据;Pp表示测试数据;Yt为训练目标值(即配方组成,用数值“0”表示不含该单色组分)。
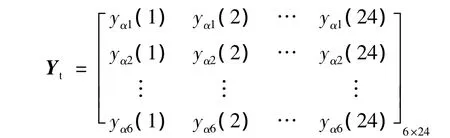
2.2 样本输入数据的获取
输入数据为样品的反射率值,因此采用Datacolor600+测色仪在 D65光源,10°视场,20mm孔径条件下测试。为了测试方便,提高测色的准确度,所有样品均先纺成纱线,再用横机加工成色纺纱织片以获得更平整的表面以及足够的测试面[8],测量时织片成4层折叠,确保不透光,每个样品取不同部位测量10次,取平均值。
2.3 BP神经网络的实现
BP神经网络采用MatLab(2011b版本)中的神经网络工具箱实现运算,在该BP神经网络中,输入层为测定样品的反射率数据,中间隐含层采用logsig函数即S型传递函数f0(x)=1/(l+e-x),输出层采用Purelin函数即线性函数f1(x)=x,输出数据为配方值,因反射率和配方值都在[0,1]范围内,均无需进行归一化。
2.4 预测准确性的评估
预测准确性采用配方比例预测偏差和预测色差2个方面来进行评估。
配方比例预测偏差采用均方根差Er来表示。
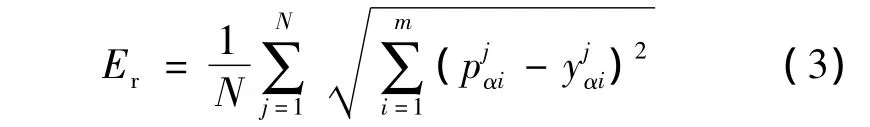
式中:N为样本数;m为单色数;pαi为预测配方;yαi为实际配方。
预测色差采用△Ecmc(2∶1)色差公式计算,即根据神经网络预报的配方Y,用相同的色纺制备工艺将其制作成色纺纱织片后由Datacolor600+测色,比较与目标色之间的色差值。
3 实验结果
3.1 学习算法对收敛速度的影响
标准的BP神经网络算法存在收敛速度慢,容易陷入局部最小值等问题,目前大都采用改进算法,包括基于梯度下降的启发性算法如附加动量法、可变学习速率法、弹性算法等以及基于最优化理论的改进算法如共轭梯度法、拟牛顿法、Levenberg-Marquardt法等[14]。将这些改进的学习算法用于本文神经网络的训练,探讨改进算法对色纺纱配色模型训练收敛速度的影响,算法中设定的参数有,隐含层节点数(神经元个数)L为6,最大循环次数为3×105,目标误差为1×10-4。经过样本训练,都能达到目标误差,但迭代时间和次数有明显差异,不同算法得到的结果见表2。其中带动量的梯度下降算法,动量因子为0.9,学习步长为0.05,其余算法均采用默认值,Er为随机抽取的3个验证样本α1-α2(10∶90),α3- α4(30∶70),α5- α6(10∶90)的配方比例平均预测偏差。
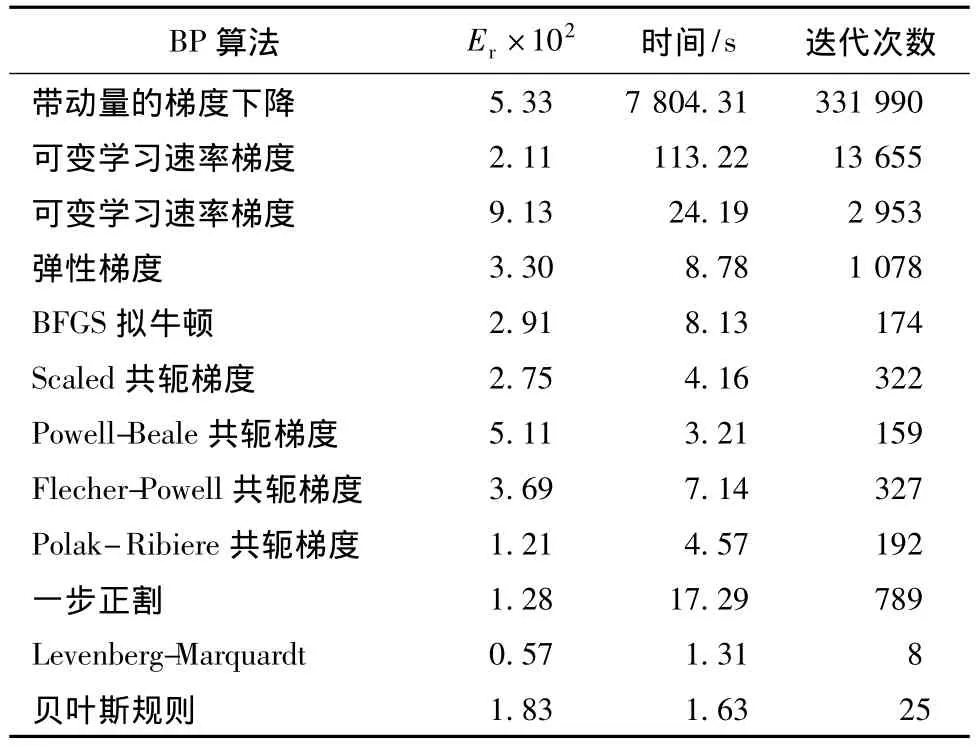
表2 不同BP算法的仿真对比Tab.2 Comparison of different BP algorithms
带动量的梯度下降算法、可变学习速率梯度算法、弹性梯度法等启发式学习方法,不但仿真时间较长,迭代次数多,而且预测误差相对较大。而最优化理论算法预测精度高,迭代时间少,速度快。本例中Levenberg-Marquardt算法是最快的算法,Levenberg-Marquardt算法训练过程中的均方误差收敛过程如图2所示。
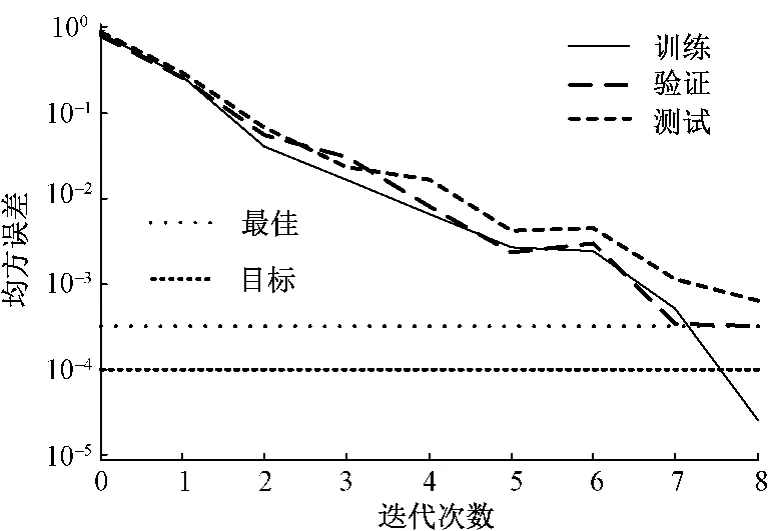
图2 训练误差的收敛过程Fig.2 Convergence process of training error
Levenberg-Marquardt算法主要通过自适应调整阻尼因子来提高收敛特性,从图2可看到,只需8次训练,本色纺纱BP神经网络训练结果就已小于设定的训练误差,且验证样本的偏差值Er在各种算法中最小,体现出很好的迭代收敛速度和优化可靠性,因此作为本模型训练的首选算法。另外,无论Polak-Ribiere共轭梯度算法还是一步正割算法或是贝叶斯规则法也都是不错的选择。
3.2 节点数对预测精度的影响
隐含层节点数对BP神经网络的预测精度有较大的影响,节点数过少,易造成网络“欠拟合”,节点数太多,易造成网络“过拟合”。在实际问题中,通常采用一些经验公式来确定隐含层节点数的大概范围,例如公式log2n<L<+c,式中:L为隐含层节点数;n、m分别为输入层和输出层的节点数;c为0~10之间的常数,因此本例中隐含层的研究范围为4~16之间,间隔为2。以Levenberg-Marquardt算法为例,用不同节点数进行训练,结果如图3所示。
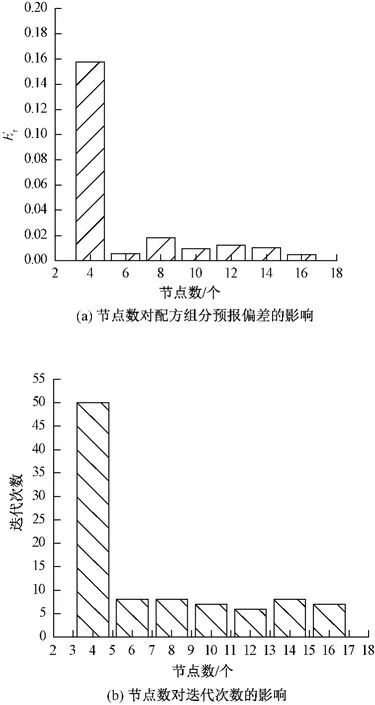
图3 节点数的影响Fig.3 Influence of number of nodes.(a)Influence of number of nodes on prediction error;(b)Influence of number of nodes on epochs
从图3可看出,配方组分预测偏差Er随着隐含层节点数的增加先显著减少再略微增大,在本文研究节点范围内,当节点数超过6个后,偏差整体变化不大,此时,迭代次数基本都保持在10以内,因此本算法采用6个节点数即可获得较小的平均预测偏差。
3.3 泛化性能
神经网络的泛化能力代表了神经网络的应用性能,用设计的6个不同配方的色纺纱样本考察构建的色纺纱BP神经网络的泛化性能,预测结果见表3。
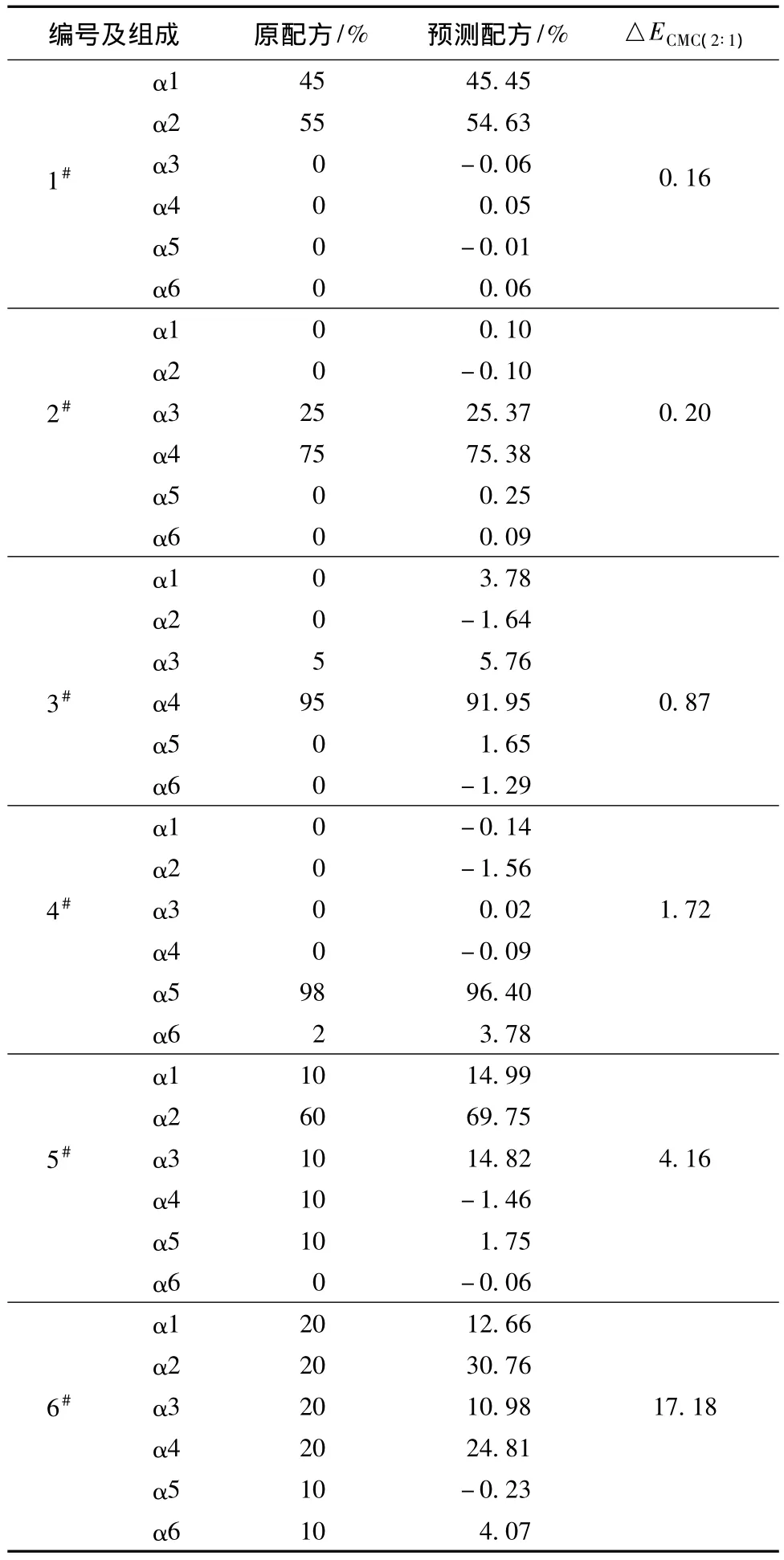
表3 色纺纱BP神经网络预测结果Tab.3 Recipe prediction results of melange yarn by BP neural network
从表3中6个测试样本的预报结果可以清晰地看到,1#和2#样品预报的配方比例与实际比例相当接近,且平均预测色差△ECMC(2∶1)只有0.18,表明预测准确度较高。3#和4#样品的预报比例偏差和预测色差都比1#和2#大,而5#和6#样品预报结果偏差更大。由于1#和2#在训练样本的训练范围内,因此显现出非常好的预测结果,而3#和4#样品虽然训练样本中有该配方组合,但配方比例值超出了训练样本值的范围,因此预测效果变差。5#和6#涉及的单色都在训练集内,但是训练样本集中没有这样的配方组合,结果预测偏差就非常大。可见,依靠神经网络进行色纺纱配色时,其泛化能力是有限的,要获得高的预测准确率,必须保证有足够数量且训练范围覆盖面广的样本集。
4 结语
本文采用BP神经网络构建色纺纱配色模型,并用简单的实验论证了模型的优劣性。仿真结果表明,构建的BP神经网络能够对训练范围内的样品进行准确的配色,相比以往基于经验或经典理论的色纺纱配色模型,基于BP神经网络的配色包含了纺纱工艺等不确定因素对颜色效果的影响,在训练样本范围内显现出更好的生产实用性,但该神经网络的泛化能力有限,如果要将该神经网络成功应用于色纺纱配色,必须首先具备非常多且覆盖面广的训练样本。分析原因,可能是该神经网络模型仅建立了色纺纱整体反射率与配方比例之间的非线性关系,并未涉及单色纤维的颜色信息,因此在下一步研究中,将考虑把单色纤维的反射率组合到该神经网络中,以期待获得更佳的泛化性能。
[1]KUBELKA P,MUNK F.Ein beitrag zur optik der farbanstriche[J].Z Tech Physik,1931,12:593 - 601.
[2]STEARNS EI, NOECHEL F. Spectrophotometric prediction of color of wool blends[J].American Dyestuff Reporter,1944,33(9):177 -180.
[3]WESTON PO. Spectrophotometer and spectrophotometric analysis and prediction:US Patent,2218357[P].1940-10-15.
[4]PHILIPS INVEMIZZIB, DUPONTD, CAZEC.Formulation of colored fiber blends from friele's theoretical model[J].Color Research and Application,2002,27(3):191 -198.
[5]BURLONE DA.Formulation of blends of precolorednylon fiber[J].Color Research and Application,1983,8(2):114-120.
[6]BURLONE DA.Theoretical and practical aspects of selected fiber-blend color formulation functions[J].Color Research and Application,1984,9(4):213 -219.
[7]李戎,宋阳,顾峰.基于Stearns-Noechel模型的纤维光谱配色算法[J].纺织学报,2007,28(1):77-80.LI Rong,SONG Yang,GU Feng.Spectrophotometric algorithm of pre-colored fiber based on Stearns-Noechel model[J].Journal of Textile Research,2007,28(1):77-80.
[8]沈加加,张志强,陈燕兵,等.基于Stearns-Noechel模型的混色毛条颜色预测[J].纺织学报,2008,29(11):61-66.SHEN Jiajia,ZHANG Zhiqiang,CHEN Yanbing,et al.Match prediction for blended color wool tops based on Stearns-Noechel model[J].Journal of Textile Research,2008,29(11):61-66.
[9]沈加加,程凤侠,陈维国,等.Stearns-Noechel模型优化及毛条混色配色系统开发[J].纺织学报,2009,30(3):121-125.SHEN Jiajia,CHENG Fengxia,CHEN Weiguo,et al.Development of color matching system for precolored wool top blends by optimized Stearns-Noechel model[J].Journal of Textile Research,2009,30(3):121-125.
[10]WESTLAND S,BISHOP JM,BUSHNELL MJ,et al.An intelligent approach to colour recipe prediction[J].Journal of the Society of Dyers and Colourists,1991,107(7):235-237.
[11]WESTLAND S,IOVINE L,BISHOP JM.Kubelka-Munk or neural networks for computer colorant formulation[C]//CHUNG ER, RODRIGUES A.Proceedings of SPIE 9th Congress of the International Colour Association.Rochester:SPIE,2001:745-748.
[12]MIZUTANI E,JANG JSR,NISHIO K,et al.Coactive neuro-fuzzy modeling for color recipe prediction[C]//Neural Networks Council Staff IEEE.Proceedings of the IEEE International Conference on Neural Networks.New York:IEEE,1995:2252- 2257.
[13]FURFERIR, GOVERNIL. Prediction of the spectrophotometric response of a carded fiber composed by different kinds of coloured raw materials:an artificial neural network-based approach[J].Color Research and Application,2011,36(3):179-191.
[14]苏高利,邓芳萍.论基于MatLab语言的BP神经网络的改进算法[J].科技通报,2003,19(2):130 -135.SU Gaoli, DENG Fangping. On the improving backpropagation algorithms of the neural networks based on MatLab language:a review[J].Bulletin of Science and Technology,2003,19(2):130 -135.

