突发性社会安全事件下的交通组织方案规划研究
高建杰
(四川警察学院 道路交通管理系,四川 泸州646000)
面对突发性社会安全事件发生时出行者出行特点的改变,决策者的交通流路径分配原则也应做出相应调整。与之相关的研究众多,文献[1]基于元胞传输模型(CTM)设计了疏散目标函数和疏散特性约束,构造了非常规突发事件影响下限定时间的区域路网疏散能力评估与交通组织设计模型;文献[2]利用专家经验法和模糊优先排序法对初拟评价指标的相关性和重要性进行了判断,构建了突发公共事件交通应急响应级别的综合评价指标体系;文献[3]从道路车辆的走行速度依赖于道路交通负荷这一交通流的重要特征出发,建立了一个动态系统的最优疏散路线与出发时间综合优化模型。文献[4]在 METANET模型的基础上考虑紧急事件所占用的车道数、进出口匝道及诱导信息对模型的影响,给出了一种双向动态的最短路径诱导算法。然而,这些研究只是针对突发事件下的某个具体问题提出的相应技术措施,在突发性社会安全事件发生后制定交通组织方案的系统性依据和实施流程方面的研究还不够。
本文以“应急救援时间最短、交通网络系统最优”为核心思想,基于标号法并考虑交通警察响应时间来设计应急救援最短路径,在分析突发性社会安全事件交通需求特征的基础上,基于可变交通需求建立系统的最优疏散路径模型。据此,提出一套突发性社会安全事件下的交通组织方案规划方法。
1 突发性社会安全事件下的交通特征分析
突发性社会安全事件的概念在《中华人民共和国突发事件应对法》中有其分类方面的规定,但并非一个法律意义上的专有名词。《国家突发公共事件总体应急预案》中用产生原因的分类法将社会安全事件分为恐怖袭击类事件、涉外类突发事件以及经济方面的突发事件等。也有学者将社会安全事件进行严格意义上的界定:由人为原因直接或间接引发的,由社会公众参与,具有组织性和目的性,对社会稳定和政府管理造成影响,引起社会矛盾或导致社会进入对峙状态的一种群体性事件。
本文将研究对象界定为突然发生的,且对社会主体的自身物质、心理及其生存环境所需的重要价值具有威肋、可能性或现实性伤害,在其产生发展过程中具有广泛地域和社会影响的社会事件。如恐怖袭击事件、经济安全事件、群体性事件等。
1.1 交通需求特征
突发性社会安全事件会对交通需求产生较大影响,使交通需求在网络上重新调整,发生结构性变化,主要表现在:
1.1.1 出行者的出行心理发生变化
突发性社会安全事件发生后,往往会引起社会公众的恐慌心理、从众心理和非理性状态,日常的交通需求会出现锐减,而追求安全保障的交通需求会骤增,某些非危险性的突发性社会安全事件甚至会吸引公众前往。
1.1.2 危险区域内出行需求量剧增
突发性社会安全事件发生后,出行者会选择从危险区域逃离到安全区域,即疏散需求。该部分的需求量可以根据危险区域内的人口数量确定,因此,对于交通管理者来说,疏散需求量是突发性社会安全事件发生后必须要疏散出去的量,是固定不变的。
1.1.3 非危险区域内出行需求变化
突发性社会安全事件发生后,路网中非危险区域内出行者的出行选择需求会受到直接影响。在突发性社会安全事件下,出行者选择是否出行、出行路径、目的地等和正常状态是不相同的,出行者考虑更多的是出行安全和路网的可靠性。因此,该部分非危险区域内交通需求是随路网的阻抗时间发生变化。
1.2 交通流特征
1.2.1 时间集中,峰值明显
突发性社会安全事件发生后,人流、车流会在短时间内聚集,交通量具有辐射效应,随着与事发地距离的增加交通流量也迅速减小。因此,短时间内,事发地局部范围内交通量聚增,峰值明显,给交通组织与管理带来极大困难。
1.2.2 方向分布系数大
突发性社会安全事件发生后,在事发地周围路网上形成的交通流量方向分布系数大,分布不均衡。道路不同方向的流量相差悬殊,主要是由于突发性社会安全事件发生开始时,救援车辆的到达和随后疏散车辆离开造成的。
1.2.3 交通流量处于饱和或超饱和状态
由于短时间内交通需求聚集,流量大,道路上的交通流基本处于饱和或超饱和状态,驾驶人的驾驶行为受前车约束明显,基本处于跟车状态。
1.2.4 非常规出行,不适用于常规的用户平衡特征
常规的交通流分配中,出行路径的选择符合用户最优原理,以出行者个体出行时间最短为原则。而突发性社会安全事件发生后,进入非常规状态,管理决策部门起主导作用,因此,适用系统最优原则,即整个交通网络系统的总出行时间最短。
2 交通组织规划方案的关键技术
2.1 基于标号法的应急救援最短路径
2.1.1 标号法的思想
标号法是由E.W.Dijkstra提出的,是目前公认的寻找最短路线问题最优方案中的有效方法,也称为Dijkstra算法。它不仅能求出从起点V1到终点Vn的最短路径,还可以得到从起点到任意一点的最短路径。
标号法基本思路为:首先从起点V1开始,给每一个顶点记一个数,称之为标号,分为T标号与P标号两种。P标号表示从起点V1到这一点的最短路权上界,称之为临时标号。P标号表示从V1到该点的最短路权,称之为固定标号,已得到P标号的点不再改变,凡是没有标上P标号的点,标上T标号。算法的每一步都会把某一点的T标号修改为P标号。经过有限步后,就可给所有点都标上P标号,即得到从起点到每一点的最短路权。
2.1.2 基于标号法设计应急救援最短路径算法
在标号法寻找最短路径思想的基础上,针对应急救援问题设计最短路径算法。主要考虑路网中所找寻的最短路径中路段和节点的总阻抗时间最小,路网拓扑结构图、路段及节点阻抗时间、交通警察响应时间为已知条件,认为若节点有可以远程操纵的管控设施,或交通警察能够在救援车辆前到达节点,则可施行交通管制,该节点的阻抗时间忽略不计。基本思路为:先利用标号法计算最短路径,然后判断最短路径是否需加入节点阻抗时间,若不需要,则算法结束,得到应急救援的最短路径;若需要,则将节点阻抗时间加到连接该节点的前一路段上,重新利用标号法计算最短路径。
假定救援车辆和交通警察在应急中心发布命令后同时出发,设定此时为0时刻,救援队伍集合、车辆启动等中间延误忽略不计。算法流程如图1所示,图中符号定义如下:
i:路径编号;
Ti(j):救援车辆到达第i条路径中第j个节点的时间,j表示节点名称;
TP(j):交通警察到达第j个节点时间,j表示节点名称,为已知条件,与交警岗亭和节点间的距离有关;
Tk(j):第j个节点阻抗时间,为已知条件,可通过长期的实测数据得到,也可参考相关文献计算得到。
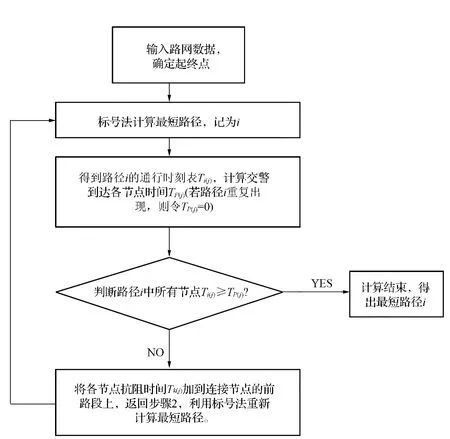
图1 最短路径计算流程
2.2 基于可变需求的最优疏散路径
2.2.1 模型
突发性社会安全事件发生后,整个区域交通系统都处于非常规状态,所有出行者的路径选择行为都应该听从交通指挥调度中心的统一协调,目的是形成区域交通网络总出行时间的最小网络流状态,该交通网络流状态通常称为系统最优。在系统最优状态下,交通网络资源得到最优利用,交通网络效益得到最大限度发挥。因此,以“系统最优”为目标的疏散路径分配模型的假设条件为所有出行者统一听从交通指挥调度中心的协调管理,在实际情况中也需要根据该模型计算结果,制定交通组织应急方案。
传统的系统最优疏散路径模型中的交通需求量固定不变,本文将交通需求量分为固定需求量与可变需求量。固定需求指的是疏散需求,这部分需求量的大小是不变的;可变需求指的是非危险区域内路网的交通需求,这部分需求量会随时间阻抗发生变化。所建立模型中的需求函数由这两部分组成,非负、连续、有下限(下限为固定需求量)和上限(上限为该区域人口规模或汽车保有量),且严格递减。交通需求函数可采用文献[9]中建议的形式。
基于可变需求的系统最优疏散路径分配模型为

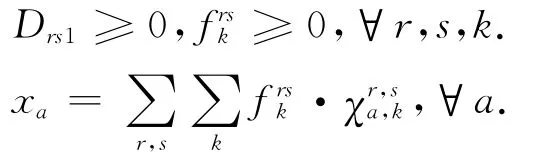
模型中所用的变量和参数:xa为路段a上的交通流量;ta为路段a的交通阻抗;ta(xa)为路段a以流量为自变量的交通阻抗函数(阻抗函数可参考文献[10]);Drs为出行需求函数;Drs0为固定出行需求量,即突发性社会安全事件发生后需疏散的交通量;Drs1为可变需求量,随阻抗时间t变化;Frs(·)为出行需求函数的反函数;Drs为起点r到终点s的总出行量的上限;fkrs为点对(r,s)间第k条路径的流量;为关系变量,若路段a在(r,s)间的第k条路径上,那么,否则
2.2.2 算法
用凸组合法(可行下降法)求解该数学规划问题,第n次迭代时的下降方向向量由从当前解到目标函数线性逼近表达式解的方向确定。从线性逼近表达式得出的线性规划是用一组辅助变量来表示,模型中的变量是路径流量{}及相应的路段流量{xa},与之对应的辅助变量定义为{}和{ya},具体计算步骤如下:
步骤3:确定下降方向。计算基于出行时间{}的OD对(r,s)间的距离,即最短路径m和相应的最短边缘出行时间的距离,再比较与的大小。若,则;若),则可取0或。所以,可以得到分配的辅助交通流模式为和
步骤4:确定步长。求解下面的一维搜索问题
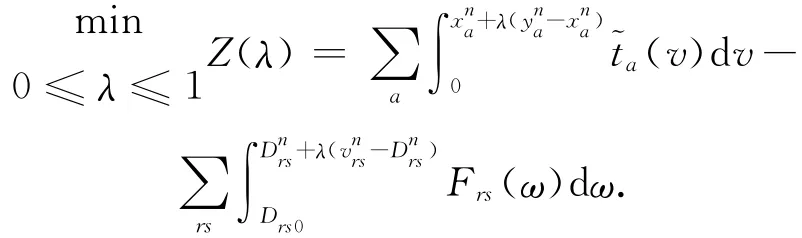
得到步长λn。
步骤6:收敛性检验。若
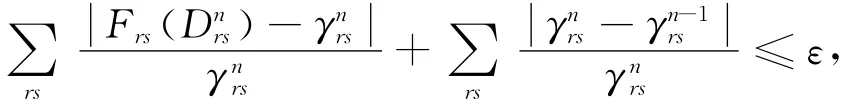
(ε为预先确定的小正数),停止计算;否则,令n=n+1,返回至步骤2。
算法结束。
3 交通组织规划方案的制定与实施
突发性社会安全事件下的交通组织规划方案的制定与实施如图2所示,该过程分为四个阶段:启动阶段,交通组织方案规划阶段,交通组织方案设计阶段,交通组织方案实施阶段。
3.1 启动阶段
突发性社会安全事件发生后,应立即进行突发性社会安全事件分析和脆弱性分析,分析内容包括事件的位置、类型、强度;事件波及人口数量和影响范围;影响区域内路网基础数据和基础设施的抗冲击能力等。根据分析结果对突发性社会安全事件进行分类、分级,对其影响程度进行评估,判断是否需要启动应急管理程序,如果结论肯定则进入交通组织方案规划阶段。
3.2 交通组织方案规划阶段
突发性社会安全事件下的交通组织方案规划是为了应急救援和疏散而对路网进行的重新分配,是保障非常态条件下交通组织的重要技术手段。该阶段主要包括交通需求分析和救援-疏散路径分配。应急救援需求分析要根据事件的影响程度配置救援人员、物资和车辆,确定救援OD(救援的起终点及数量);疏散需求分析要对疏散区域进行分析,根据事件影响确定需要疏散的人数,选择避难所,确定疏散OD(疏散的起终点及数量)。根据需求分析结果,利用关键技术中提到的救援-疏散路径分配计算方法,得到救援路径、疏散路径及路网重新分配结果。
3.3 交通组织方案设计阶段
根据路网重新分配结果,对整个路网承载力进行评估,判断路网是否超载,形成针对路网薄弱环节的交通组织方案,结合保障救援需求的交通组织方案和保障疏散需求的交通组织方案,评价交通组织方案是否可行,评价指标主要是人员的安全疏散、救援的及时、路网的承载能力等。若交通组织方案不可行,决策组织应实施交通管制的权利,再重新调整规划,直至交通组织方案可行。
3.4 交通组织方案实施阶段
首先需要以政府为主导的具体职能部门,保障交通组织方案的执行,如通过警车引导救援与疏散的车流。此外,应实时监控路网交通流的运行状态,一旦发生拥堵,应快速响应,启动疏堵方案,并实时反馈路网信息给指挥中心,以重新评估路网调整的交通组织方案,保障交通组织方案的有序实施。
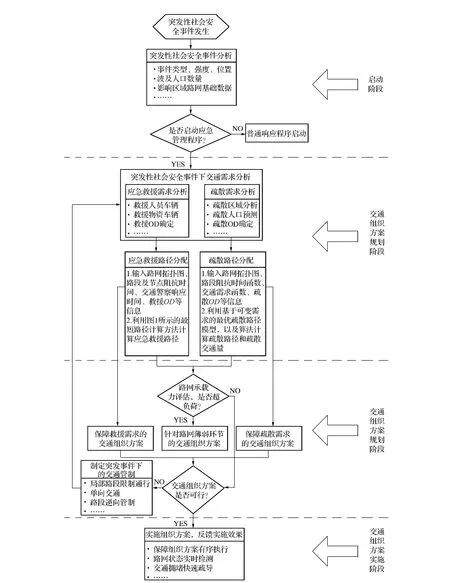
图2 突发性社会安全事件下的交通组织规划方案的制定与实施
4 结束语
本文给出一套突发性社会安全事件影响下的交通组织方案规划理论与方法,为突发性社会安全事件下决策者制定救援疏散路线提供了技术支撑,也为交通管理部门制定交通组织方案提供依据。模型中的疏散需求量根据危险区域内的人口数量来确定,而危险区域范围的界定需要结合应急管理需求的研究内容。
[1] 王永明,周磊山,刘铁民.非常规突发事件中的区域路网疏散能力评估与交通组织方案设计[J].系统工程理论与实践,2011,31(8):1608-1616.
[2] 何雅琴,李杰.城市突发公共事件交通应急响应级别评价指标体系[J].公路交通科技,2012,29(6):116-120.
[3] 覃媛媛,李文勇,张永捷,等.城市突发事件下交通影响范围方法比较[J].交通科技与经济,2014,16(3):1-3.
[4] 高明霞,贺国光.动态系统最优的疏散路线与出发时间综合优化模型[J].系统工程,2009,27(6):73-77.
[5] 任子晖,王坚.紧急事件的动态交通流模型及双向动态最短 路诱 导 算 法 [J].计算 机 应 用,2008,28(11):2955-2957.
[6] 肖遥.社会安全事件网络舆论演变研究[D].武汉:华中科技大学,2013.
[7] 王永明.非常态事件影响下的交通组织规划及交通流模拟研究[D].北京:北京交通大学,2009.
[8] 冯佩雨.突发事件下城市交通紧急疏散的研究[D].成都:西南交通大学,2008.
[9] 王炜,陆建.道路交通工程系统分析方法[M].北京:人民交通出版社,2011.
[10]公维勇,高建杰,焦海贤.城市交通空间需求与交通网络双均衡研究[J].重庆交通大学学报:自然科学版,2011,30(3):429-431.
[11]何南,赵胜川.城市道路阻抗函数模型研究——以大连市为例[J].公路交通科技,2014,31(2):105-108.
[12]SHEFF Y.Urban Transportation Network:Equilibrium Analysis with Mathematical Programming Methods[M].Englewood Cliffs:Prentice-Hall,1985.

