单目摄像机与三维激光雷达联合标定的研究

魏克全，时兆峰，李 晗，郝 鹏

(北京自动化控制设备研究所，北京100074)



单目摄像机与三维激光雷达联合标定的研究

魏克全，时兆峰，李 晗，郝 鹏

(北京自动化控制设备研究所，北京100074)

为解决单目摄像机与三维激光雷达组成的传感系统中数据匹配的问题，文章采用基于平面特征的方法实现了两传感器的联合标定，提出了通过优化平面靶标摆放位置来减少样本数量并提高样本质量，保证标定精度的方法。通过建立数学模型和实验验证了本文方法及算法的正确性，当靶标位置均匀分布在摄像机视场内，并且法向量方向均匀分布在四个象限时，只需4个标定位置即可完成参数求解，且标定误差与使用16个位置时相当。

联合标定；单目摄像机；三维激光雷达；平面特征；匹配融合

0 引言

激光雷达与摄像机的组合传感系统作为无人车环境感知的重要技术手段，已经得到广泛的研究与应用。由于两传感器获得的数据是在各自坐标系下的表示，而数据融合需将两者数据表示在同一坐标系下，因此需要通过联合标定来确定两坐标系中对应点之间的转换关系，即旋转矩阵和平移向量。

联合标定通常是利用标定物的特征在两传感器坐标系中的坐标来构建参数求解方程。常用的特征主要有点[2]、直线和平面特征[3]，其中使用平面特征的方法可以避免混合像素现象的影响，因而被广泛采用。Zhang和Pless等[4]较早提出了一种基于平面标定板的标定方法，指出了标定板平面和激光扫描平面间的夹角会对整个标定精度产生影响。项志宇等[5]也利用传感器原点到靶标平面的距离对应性实现了联合标定，其只要求有多个位置的靶标数据，并未研究靶标摆放位置对结果的影响，并给出满足精度要求时所需的最少位置数，不利于标定效率的提高和标定的流程化，以及组合传感系统的产品化。

本文在文献[5]的基础上进行了单目摄像机与三维激光雷达联合标定的研究，提出了一种重投影误差的计算方法，并提出了通过优化靶标摆放位置来减小位置随意性对结果的影响，缩短标定时间，简化标定流程的方法。

1 联合标定数学模型

联合标定中各坐标系关系如图1所示。其中，OwXwYwZw为标定板坐标系，OcXcYcZc为摄像机坐标系，OlXlYlZl为激光雷达坐标系，T为两坐标系之间的平移向量，两坐标系下标定板的单位法向量为Pci和Pli，两坐标系原点到标定板坐标系原点的平移向量为tci和tli。

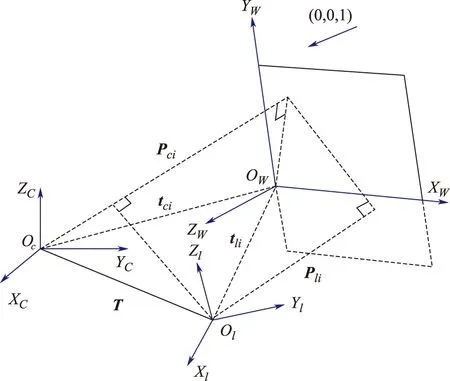
图1 联合标定坐标系关系Fig.1 Relation of coordinate system in joint calibration

设两坐标系之间的转换关系为

(1)

(2)

其解析解为R′=VUT[6]。其中，USVT=PlPcT为矩阵奇异值分解[7]。

由坐标系关系可知，两坐标系原点到标定平面的距离差为

PciT=‖Pcitci‖-‖Plitli‖

(3)

对于n个标定位置，取目标函数为

(4)

(5)

1.1 摄像机中靶标平面参数求取

本文首先采用张正友法[8]进行摄像机内参数标定，然后计算出摄像机坐标系中标定物平面的法向量以及平面到坐标系原点的距离。

首先定义图像像素直角坐标系，原点O定义在图像平面的左上角，像素坐标(u，v)表示该像素在像素数组中的列数和行数。再建立以长度单位表示的图像物理坐标系，原点O′定义在主点(即摄像机光轴与图像平面的交点)，x、y轴分别平行于u、v轴。最后定义摄像机直角坐标系，原点Oc定义在摄像机的光心，Xc、Yc轴分别平行于x、y轴，Zc轴为光轴。摄像机各坐标系关系如图2所示。

图2 摄像机坐标系与图像像素坐标系及物理坐标系Fig.2 Coordinate system of camera andcoordinate system of pixel and physical image

设空间某点p的坐标为(xc，yc，zc)，其图像物理坐标为(x，y)，像素坐标为(u，v)，设摄像机焦距为f，主点的像素坐标为(u0，v0)，dx、dy分别为x、y轴方向上单位像素间的物理距离，则由小孔成像原理可得图像像素坐标与摄像机三维坐标之间的关系为

(6)

其中，矩阵M为摄像机的内参数矩阵。

设标定板平面直角坐标系为OwXwYwZw，原点定义在标定板的一个顶点，两条边分别为Xw、Yw轴，Zw轴垂直于标定板平面，则摄像机坐标系与标定板平面坐标系之间的转换关系为

(7)

其中，R1为旋转矩阵，t为平移向量。由摄像机标定原理可知，当有至少3个标定位置下的标定板图像时，即可解得内参数矩阵M，进而解出每个标定位置下的R1和t。取标定板平面直角坐标系下标定板的法向量为(0，0，1)T，则摄像机坐标系下R1第三列即为此标定板的法向量方向，R1*t即为标定板到摄像机坐标系原点的距离。

1.2 激光雷达点云平面拟合

本文采用HDL-64E[9]三维激光雷达，其内部含有64个激光器，通过旋转扫描可获取垂直26.8°、水平360°视场的三维环境点云图像。定义激光雷达坐标系，原点Ol在第32与33个激光器之间，Xl轴、Yl轴分别平行于基座的两边，Zl轴定义在旋转轴上，如图3所示。

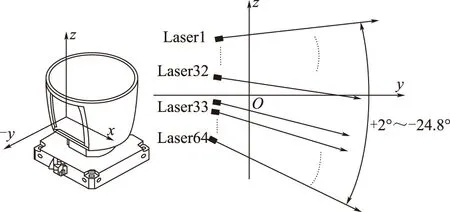
图3 激光雷达坐标系Fig.3 Coordinate system of laser radar

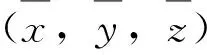
1.3 位置影响分析

令Pci=(xiyizi)，‖Pcitci‖-‖Plitli‖=mi，则可得

(xiyizi)·T=mi

(8)

式(8)将参数求解问题转化为由点(xiyizi)拟合平面t1xi+t2yi+t3zi=mi的问题。理论上3个不共线的点成等边三角形分布时，平面拟合的抗噪声效果最好，因此当3个法向量成等夹角分布时，T的求解精度最高。

在实际标定时，标定板成3个位置等夹角摆放较难操作，易引入随机误差，因此可以设置4个标定位置，使标定板均匀分布在摄像机视场内且平面法向量均匀分布于四个象限内，以便在保证样本质量的情况下减少样本数量。

2 标定实验

本文使用分辨率1024×768像素、水平视场90°的摄像机进行实验。标定板为1m×1m的平板，画有9×7个边长10cm的黑白格。两者安装位置为：摄像机镜头在雷达中心前方15cm左右，下方20cm左右，左右方向两者大致重合，系统实物如图4所示。

图4 传感器安装位置关系Fig.4 Fix position of sensors

首先采用Matlab标定工具箱完成摄像机标定，摄像机标定得到的内参数(像素单位)为

然后进行联合标定，实验时在传感器前方2～5m距离内，以摄像机光轴为对称轴，选取了16个摆放位置并按位置数不同进行了5组实验，摆放位置示意图如图5所示。

图5 摄像机坐标系下各标定位置示意图Fig.5 Position of calibrationboard in camera coordinate

图5 摄像机坐标系下各标定位置示意图(续)Fig.5 Position of calibrationboard in camera coordinate

本文采用重投影误差评价标定精度，即计算点云投影后的边缘与图像中标定板边缘的最大偏移像素数。重投影偏差示意图如图6所示，红线为摄像机图像的标定板边缘，绿线为重投影边缘。分组试验结果对比如表1所示。

图6 一种重投影误差示意图Fig.6 Sketch map ofa kind of re-projection error

由实验结果看，采用平面靶标会由于位置摆放的不定性造成原始数据不充分而影响标定精度，通过考虑标定位置的对称性可在一定程度上减小此影响，最少只需4个标定位置即可达到使用16个位置时的精度，因此可极大地提高标定效率，有利于组合传感系统产品标定的流程化。最后本文通过OpenCV及OpenGL程序分别进行了点云投影和场景三维显示的工作，显示效果如图7、图8所示。

表1 分组试验结果对比Tab.1 contrast of grouping experiment

图7 投影场景Fig.7 Projection scene

图8 三维显示场景Fig.8 3D scene

3 结论

本文利用平面靶标，采用基于平面特征的联合标定方法完成了单目摄像机与三维激光雷达的联合标定。首先建立数学模型，然后进行实验数据采集，最后完成参数求解。经多次实验得出了正确的结果，两传感器数据匹配较好。通过优化靶标摆放位置，减小了位置随意性对结果的影响，仅需采集4个标定位置的数据，缩短了标定时间。后续将进行算法及结果优化，进一步提高标定精度及数据处理速度。

[1] 郁肖飞，史朝龙，李新纯，李晗.多光束三维成像激光扫描系统校准方法研究[J].战术导弹技术，2013，1：92-98.

[2] 林鸿生，胡春生.三维成像激光雷达图像与摄像机图像的融合[J].内燃机与动力装置，2009，6(s)：1-4.

[3] 李琳，张旭，屠大维.二维和三维视觉传感集成系统联合标定方法[J].仪器仪表学报，2012，33(11)：2474-2479.

[4] Zhang Q L，Pless R.Extrinsic calibration of a Camera and laser range finder(improves camera calibration)[C].IEEE International Conference on Intelligent Robots and Systems(IROS)，2004，3：2301-2306.

[5] 项志宇，郑路.摄像机与3D激光雷达联合标定的新方法[J].浙江大学学报(工学版)，2009，43(8)：1401- 1405.

[6] Bauermanni，Steinbach.Joint calibration o f a range and visual sensor for the acquisition of RGBZ concentric Mosaics Erlangen[C].Proceedings of VMV2005.Erlangen：Elsevier，2005：666-672.

[7] Schonem Ann P H.A generalized solution of the orthogonal procrustes problem[J].Psychometrika，1966，31(1)：1-10.

[8] Zhang Zh Y.Flexible camera calibration by viewing a plane from unknown orientations.Microsoft Research，One Microsoft Way，Redmond，WA 98052-6399，USA

[9] HDL 64E-S2 User’s Manual.Velodyne Lidar Inc，345 Digital Drive，Morgan Hill，CA 95037，2011.

[10] Smith L I.A Tutorial on Principal Components Analysis.[EB/OL].2006-05-18.

Research on the Joint Calibration of Monocular Camera and 3D Lidar

WEI Ke-quan，SHI Zhao-feng，LI Han，HAO Peng

(Beijing Automatic Control Equipment Institute，Beijing 100074，China)

To solve the problem of data matching in the sensor system composed of monocular camera and 3D lidar，we accomplish the joint calibration of the two sensors using the method basing on the planar feature and present a method to reduce the amount and improve the quality of samples by optimizing the position of calibration board in this paper.We prove the method and the algorithm by founding the mathematical model and simulation and experiments.The error appears minor when the positions of the board scatter evenly in the camera field of view and just need 4 calibration positions to accomplish the calibration.

Joint calibration；Monocular camera；3D lidar；Plane feature；Match and fusion

2014 - 10 - 30；

2015 - 04 - 30。

魏克全(1989 - )，男，硕士，主要从事激光雷达及图像的数据处理工作。

E-mail：weikequan163@163.com

TP391.41;TN958.98

A

2095-8110(2015)06-0069-06