攻击时间约束下的三维制导律

王 健，刘远帆，史 震

(哈尔滨工程大学 自动化学院，哈尔滨150001)



攻击时间约束下的三维制导律

王 健，刘远帆，史 震

(哈尔滨工程大学 自动化学院，哈尔滨150001)

基于三维空间内导弹-目标的相对运动方程，针对固定目标，提出了一种攻击时间约束下的多导弹协同攻击的三维制导律。俯仰通道设计了滑模变结构制导律,偏航通道基于动态逆控制理论，采用机动控制，调整导弹的攻击时间，使其趋于指定值，并与在俯仰通道采用推导的增广比例制导律作了比较。最后，仿真结果表明，该制导律最终能使攻击的剩余时间误差趋于零，能够满足对制导精度和攻击时间的要求，证明了算法的正确性和优越性。

攻击时间约束；动态逆控制；滑模变结构；增广比例；制导律

0 引言

当多导弹协同攻击同一目标时，为了提高导弹的突防能力，通常采用饱和攻击战术，需要对导弹的攻击时间进行精确的控制。文献[1]基于线性化的弹目相对运动方程，采用最优控制的方法来调节反馈的攻击时间误差(即比例导引律预测的攻击时间与指定的攻击时间之差)，实现了对攻击时间的控制。文献[2]在制导指令中引进了一个含有3个未知系数的扩充多项式，来分别决定导弹的攻击时间、攻击角度和脱靶量，同时实现了导弹对攻击时间和角度的要求。文献[3]提出了一种两阶段控制的方法，来同时控制撞击时间和撞击角度，第一阶段对时间精控和角度粗控；第二阶段实现对角度的精确控制。

本文提出了攻击时间约束下打击固定目标的三维制导律。通过对弹目运动方程的分析，在俯仰通道采用滑模变结构控制，在偏航通道采用动态逆控制，保证在击中目标的同时，调节导弹的攻击时间，使其趋于指定值，实现多导弹的协同攻击，并与将俯仰通道的控制量修改为推导的增广比例制导律作比较，证明了算法的优越性。

1 三维导引问题描述

导弹和目标都看作质点，目标静止且导弹恒速运动，导弹和目标的相对运动关系如图1所示。

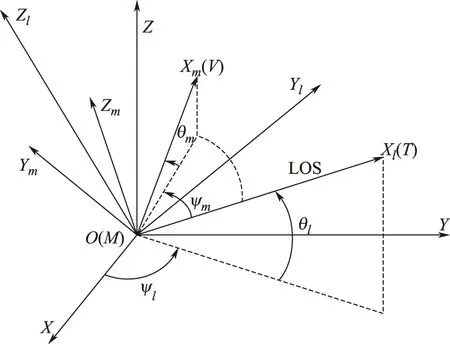
图1 导弹和目标的相对运动关系Fig.1 Engagement geometry of missile and target

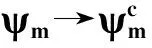
在图1中，XYZ表示参考坐标系，XlYlZl表示视线坐标系，XmYmZm表示弹体坐标系，R表示弹目距离，V表示导弹的速度并且是常值；θm和ψm分别是导弹速度矢量相对视线坐标系的高低角和方位角，θl和ψl分别是弹目视线角(LOS)相对参考坐标系的高低角和方位角。Aym和Azm分别为导弹的偏航和俯仰的加速度指令。导弹相对目标的动力学运动方程[4]：

(1)

(2)

(3)

(4)

(5)

(6)

用Td表示指定的攻击时间，t为时间变量，则期望的剩余攻击时间tgo可以表示为

tgo=Td-t

(7)

则攻击时间误差et可以表示为

(8)

2 攻击时间约束的制导律设计

在本节，对导弹俯仰和偏航通道的控制指令分别进行设计，使其在指定的时间命中目标。在偏航通道，依据动态逆控制理论，设计相应的制导律使导弹的剩余时间误差et趋于零；在俯仰通道，分别依据变结构和李雅普诺夫稳定理论，设计了相应的变结构制导律和增广的比例制导律。

2.1 动态逆制导律的设计[5]

为了通过对偏航通道的控制来调节攻击时间，在本节，偏航通道采用了动态逆控制。

对式(8)求导，并结合式(1)、式(6)～式(8)，可得

(9)

(10)

期望的慢子系统可以定义为

(11)

(12)

(13)

d1可以用式(14)表示

(14)

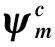
(15)

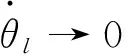
对式(15)两边求导，结合式(9)，可得

(16)

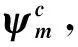
(17)

(18)

2.2 滑模变结构制导律的设计[6-7]

对式(2)的两边求导，并将式(4)代入可得：

(19)

(20)

(21)

同理对式(3)的两边求导，并将式(5)代入可得：

(22)

(23)

(24)

在俯仰通道上，选取滑模面为

(25)

对式(25)求导可得

(26)

为了保证系统的状态能够到达滑模面，并且具有良好的动态特性，在俯仰通道采用自适应滑模趋近律

(27)

综合上面各式可以得到俯仰通道的加速度指令Azm1

(28)

同理，对于偏航通道，选取滑模面和趋近律分别为：

(29)

(30)

其中，K2、ε2>0且为常数。代入可以得到偏航的加速度指令Aym1

(31)

2.3 增广比例制导律的设计

(32)

(33)

(34)

根据李雅普诺夫稳定性理论，选取李雅普诺夫函数为：

(35)

(36)

(37)

对式(35)的两边求导并将式(36)和式(37)代入可得

(38)

根据式(38)，选取增广比例制导律中俯仰通道的控制量Azm2和偏航通道的控制量Aym2分别为：

(39)

(40)

其中，N1>1，N2>1，将式(39)和式(40)代入式(38)，可以得到

(41)

3 仿真实例和分析

3.1 攻击时间约束下的制导律的仿真和分析

在本节，俯仰通道采用2.2节的滑模变结构控制，得到俯仰通道的控制量Azm1，而在偏航通道则采用2.1节的动态逆控制，得到偏航通道的制导指令Aym。假设四枚导弹同时攻击同一个固定的目标，仿真的初始参数见表1。指定的攻击时间设置为40s，控制器的其他的仿真参数d2=k1=10，c1=c2=0.9，δ=0.01，ε1=0.02，仿真步长设置为Δt=0.001s，导弹最大的法向过载设置为8g。仿真结果如图2和图3所示。

表1 仿真的初始参数Tab.1 Initial conditions of the missiles engagement

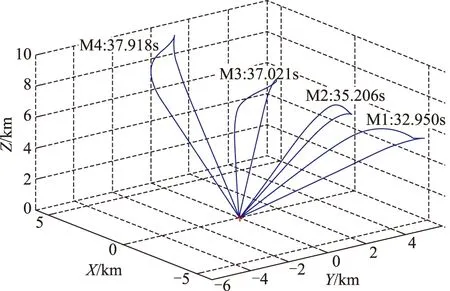
图2 三维的弹道轨迹和导引时间Fig.2 3-D Trajectories and guidance time by impact time constrained control

图3 四发导弹协同攻击下的弹目距离Fig.3 Relative distances between the target and missile in four missiles cooperative attack

在图2中，比较陡直的曲线是导弹的俯仰和偏航通道采用2.2节推导的滑模变结构制导律下生成的，可以看出，各个导弹击中目标的时间不同，而弹道比较弯曲的曲线是采用本节的制导律下生成的，结合图3表明，虽然仿真的初始条件不同，但是四枚导弹在所设计制导律的导引下都能在指定的攻击时间40s时命中同一目标，相应的Missile1～Missile4各个导弹的脱靶量分别为0.3000m、0.2800m、0.2400m和0.3000m，脱靶量的误差在1m以内，因此导弹在攻击时间约束的同时实现了对目标的精确打击，证明了算法的正确性和有效性。

3.2 攻击时间约束下的制导律的比较

在3.1节中，俯仰通道采用滑模控制，偏航通道采用的是动态逆控制，称为方法1；而将俯仰通道控制量改换为2.3节推导的增广比例制导律中相应的控制量Azm2，而偏航通道仍采用的是2.1节所推导的偏航通道的控制量Aym，称为方法2，将两种方法通过仿真进行比较。

以某空对地导弹为例，攻击的目标为固定的，导弹的初始位置坐标为(-6，5，6)km，目标的位置坐标为(0，0，0)km，导弹的速度为V=300m/s，初始的高低角θm0=20°，方位角ψm0=15°，指定的攻击时间设置为42s，k1=15，N1=15，d2=10，c1=c2=0.9，仿真步长设置为Δt=0.001s，δ=0.01，ε1=0.02，导弹最大的法向过载设置为8g，仿真结果如图4～图9所示。

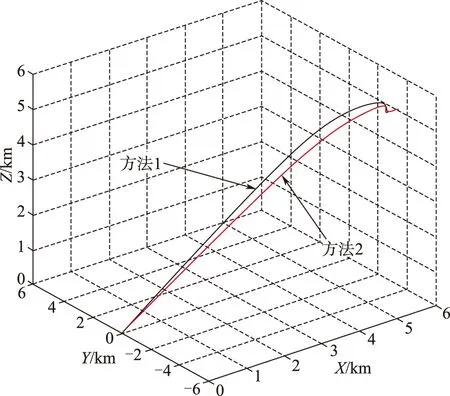
图4 三维的弹道轨迹Fig.4 3-D trajectories

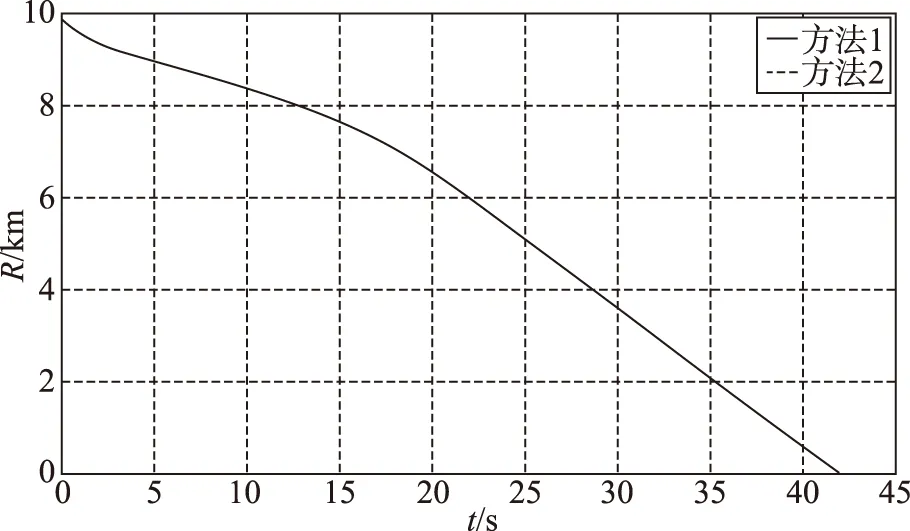
图5 弹目之间的相对距离Fig.5 Relative distances between the target and missile

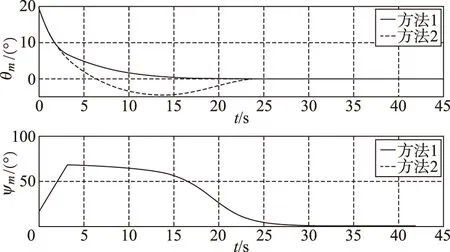
图6 前置角的变化曲线Fig.6 Curves of heading angles

图7 视线角速率的变化曲线Fig.7 Curves of line-of-sight angle rate

图8 加速度的变化曲线Fig.8 Curves of missiles’ acceleration

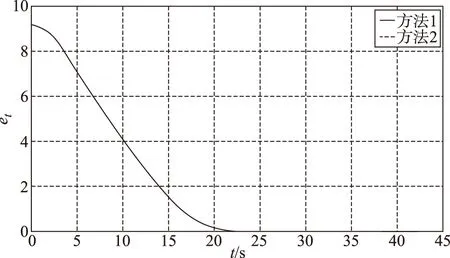
图9 攻击时间误差的变化曲线Fig.9 Curves of time-to-go error

由图9可知，导弹的攻击时间误差最终收敛到零，结合图4和图5表明，导弹在这两种制导律的导引下都能在指定的攻击时间42s时命中目标，方法1的脱靶量为0.2166m，方法2的脱靶量为0.8152m，则说明方法1在俯仰通道采用滑模的控制方法有更高的制导精度。图5和图9还可以看出，两种导引方法下的弹目距离和导弹的攻击时间误差曲线几乎重合，这是因为它们的曲线主要取决于偏航通道的机动控制指令，而这两种导引方法下偏航通道的制导指令是一样的。

在图4中，由于偏航通道都采用的是动态逆控制，则在两种方法的导引下，导弹在导引前期由于要通过较大的机动来调节飞行时间，所以弹道比较弯曲，而在导引后期，机动较小，弹道比较平直。如图8所示，由于在偏航通道机动较大，因此偏航的加速度指令Aym与俯仰的加速度指令Azm1或Azm2相比，曲线的波动较大。在图6中，导弹的前置角θm和ψm也都逐渐收敛到零，同样与θm相比，ψm在整个制导的过程中曲线的波动较大。图7则表明导弹俯仰和偏航通道的视线角速率都最终收敛到零，以实现对目标的精确打击。

4 结论

运用滑模变结构和动态逆控制理论，设计了攻击时间约束下打击固定目标的三维制导律，并与将俯仰通道的控制量修改为推导的增广比例制导律作了比较，仿真的结果验证了本文所设计的制导律的有效性和优越性。

[1] Jeon I S，Lee J I，Tahk M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Trans.on Control System Technology，2006，14(2)：260-266.

[2] Kim T H，Lee C H，Jeon I S，Tahk M J.Augmented polyno-mial guidance with impact time and angle constraints[J].IEEE Transactions on Aerospace and Electronic System，2012，49(4)：2806-2817.

[3] 张友根，张友安.控制撞击时间与角度的三维导引律：一种两阶段控制方法[J].控制理论与应用，2010，27(10)：1429-1434.

[4] Song S H，Ha I J.A lyapunov-like approach to performance analysis of three-dimensional pure PNG laws[J].IEEE Transactions on Aerospace and Electronic System，1994，30(1)：239-247.

[5] 张友安，马国欣.攻击时间控制的动态逆三维制导律[J].哈尔滨工程大学学报，2010，31(2)：215-219.

[6] Shashi Ranjan Kumar，Debasish Ghose.Three dimensional imp-act angle constrained guidance law using sliding mode control[C].2014 American Control Conference，Portland，Oregon，USA，June 4-6，2014：2474-2479.

[7] 周荻.寻的导弹新型导引规律[M].北京：国防工业出版社，2002：8-26.

Three-dimensional Guidance Law with Impact Time Constraint

WANG Jian，LIU Yuan-fan，SHI Zhen

(College of Automation，Harbin Engineering University，Harbin 150001，China)

Based on the missile-target relative motion equations in the three-dimensional space，a impact time constrained three-dimensional guidance law was deduced for multiple missiles in attacking a stationary target simultaneously at the desired impact time.A sliding mode variable structure guidance law was adopted in the pitch channel and the yaw channel was controlled by a maneuver control system using the dynamic inversion control，the maneuver control instruction was able to adjust the impact time to a designated value，and the pitch control command was revised as the instruction of the derived augmented proportional guidance law for comparison.Finally，numerical simulation results demonstrate that the proposed guidance law can make time-to-go error be ultimately reduced to zero and satisfies the requirements of the impact time as well as the guidance precision，the validity and superiority of the algorithm is confirmed.

Impact time constrained；Dynamic inversion control；Sliding mode variable structure；Augmented proportional；Guidance law

2015 - 06 - 10；

2015 - 07 - 10。

王健(1988 - )，男，硕士，主要研究方向是导弹的制导与控制。

E-mail：wangjian411@hrbeu.edu.cn

TJ765.3

A

2095-8110(2015)06-0012-07