电压不平衡且畸变下基于平均值环节锁相环的研究

闫斌斌,贾焦心

(1.东北电力大学 电气工程学院,吉林 吉林 132012;2,北方工业大学 电气与控制工程学院 北京 100144)

电压不平衡且畸变下基于平均值环节锁相环的研究

闫斌斌1,贾焦心2

(1.东北电力大学 电气工程学院,吉林 吉林 132012;2,北方工业大学 电气与控制工程学院 北京 100144)

针对传统的基于同步参考坐标系的三相锁相环(SRF-PLL) 在非理想电网环境下不能准确跟踪电网电压相位的问题,提出采用一种正反dq坐标变换和平均值环节的锁相方法,通过平均值环节将系统电压的正序基波分量提取出来,利用频率反馈环把周期值反馈给平均值环节模块实现频率自适应。仿真结果表明,在三相电压不平衡且严重畸变的条件下,该方法能快速准确地实现基波的正序分离从而锁定电网电压的相位和频率,验证了其有效性。

电压畸变;正反dq坐标变换;平均值环节;锁相环

在新能源发电系统中,只有在锁相环(PLL)不断监测和反馈准确的电网电压信息的情况下,并网逆变器才能正常工作。传统的锁相环结构比较简单,实时性强,无需复杂的数学坐标运算,然而在电网电压不平衡或电压严重畸变时,锁相产生了振荡,不能有效地完成锁相。文献[1-2] 提出基于对称分量法的锁相环技术,可以减弱负序分量在正序分量上的二倍频扰动影响,但对电网电压频率要求高,适合频率固定的场合。文献[3-4]通过双同步坐标系解耦的锁相环技术消除负序分量在正序分量上的二次谐波影响,将得到的正序分量作为锁相环的参考基准。文献[5-7]提出基于二阶广义积分型的锁相技术，可以滤除电网电压中谐波影响和实现三相电压正负序的分离,但是电网频率突变时系统动态响应速度慢、检测精度不足。目前,SPLL通常采用低通滤波器LPF[8-10]来提高锁相精确度,但是LPF不能使负序基波分量得到完全分离,且其滤波性能和动态性能往往是矛盾的。以上锁相技术在电网电压不平衡和严重畸变时不能快速精确地检测电压相位。基于此,本文提出采用一种正反dq坐标变换和平均值环节的锁相方法,通过正反dq变换和平均值环节来消除谐波,以有效地消除负序分量和谐波分量的影响,精确得到基波正序分量;通过构造频率反馈环,保证了系统能够快速准确地跟踪电网电压的频率和相位,进而实现频率的自动跟踪。仿真表明,该方法能快速、准确地实现基波的正序分离,并具有自适应性和抗谐波干扰能力的优点。

1 基于dq 坐标变换的锁相环分析

1.1 三相电压平衡没有畸变

三相电网电压向量usa、usb、usc可以表示为

式中:UP为电压的幅值,θp为电网输入相位角。

对usa、usb、usc信号进行Clark变换得

经过同步旋转坐标θ的Park变换得

由此可知,将Uq作为控制对象,在相位锁定时为Uq=0,通过闭环控制使θ与θp同步变换来完成锁相。

1.2 三相电压不平衡且有畸变

在实际电力系统中偶次谐波分量很小,对锁相输出影响很小,所以系统电压畸变时,主要考虑奇次谐波。当系统电压不平衡且存在畸变时,电压表达式为

式中:右侧各项依次为三相系统电压的正序基波分量、正序谐波分量、负序基波分量和负序谐波分量;UP、Upk、Un、Unk和θp,θpk,θn,θnk分别为上述各项的幅值和初相位;k为谐波次数,取k=3,5,7，…。

系统电压经过dq坐标变化后得到

当三相电压不平衡且有畸变时,经dq变换后,传统的RSF-PLL不能消除负序分量和谐波的影响,Usq,Usd中存在交流量,不能很好地跟踪相角和频率。

2 电网同步技术原理与结构

2.1 平均值环节消除谐波原理

由于Usq,Usd中的交流量的频率均为工频的整数倍,故可通过积分区间为工频周期的平均值环节将之全部滤除,只余下直流量Upd,Upq(对应Usa,Usb,Usc的正序基波分量)。电压平均值环节如图1所示,工作原理为:利用电压在区间[0,T]的积分值除以积分区间T;通过积分模块的输出减去延迟模块的输出(电压积分延迟T的值)得到区间[0,T]的积分值。

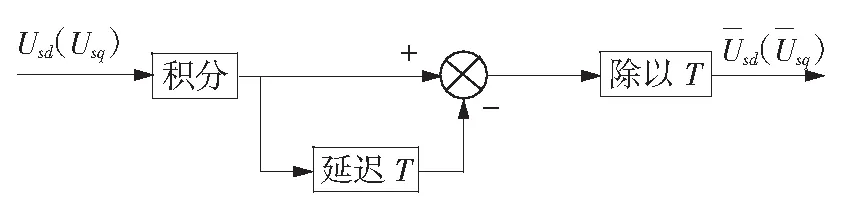
图1 电压平均值环节

根据图1得到的Upd,Upq为

2.2 同步检测系统的结构

首先通过基于任意工频旋转角的正反两次dq变换和平均值环节将系统电压的正序基波分量提取出来,然后经过dq变换锁相。另外考虑到实际电网频率可能会在工频附近出现扰动,影响到平均值环节模块消除dq轴上正弦交流分量的效果,故构造频率反馈环,将检测到的基波频率经低通滤波器LFP滤除高频噪音,再换算成周期值并反馈给平均值环节模块,保证了系统能自适应地跟踪实际电网频率的变化。PLL的具体框图如图2所示。

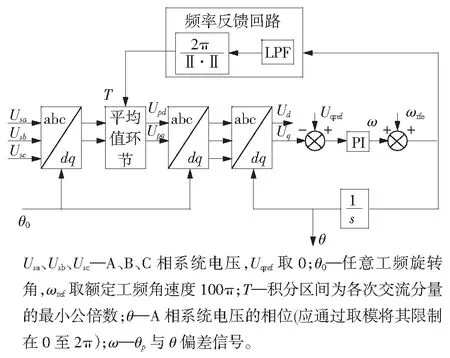
图2 PLL的具体框图

3 仿真研究

根据系统框图,采用MATLAB/simulink搭建系统仿真模型如图3所示。

仿真系统中,PLL的参数如下:kp=10,ki=500,ωref=314 rad/s,电网电压幅值取标幺值;传统的SRF-PLL的参数为kp=4.5,ki=347.8。分别在电网电压不平衡频率突变和谐波畸变等情况下对传统的SRF-PLL和基于平均值环节的锁相环进行了仿真。

3.1 电网电压不平衡和频率突变的仿真

当输入电压信号在0.15 s时注入幅值为0.1 p.u.的负序基波电压和0.1 p.u.零序电压,频率突升为55 Hz,两种电压同步技术的响应如图4所示。

图4 电压不平衡和频率突变的仿真

由图4可知,传统的SRF-PLL在0.03 s后可以完成锁相且相位有波动,基于平均值环节的PLL在突变时刻的抖动很小并且经过0.01 s后角频率和相位准确锁定。

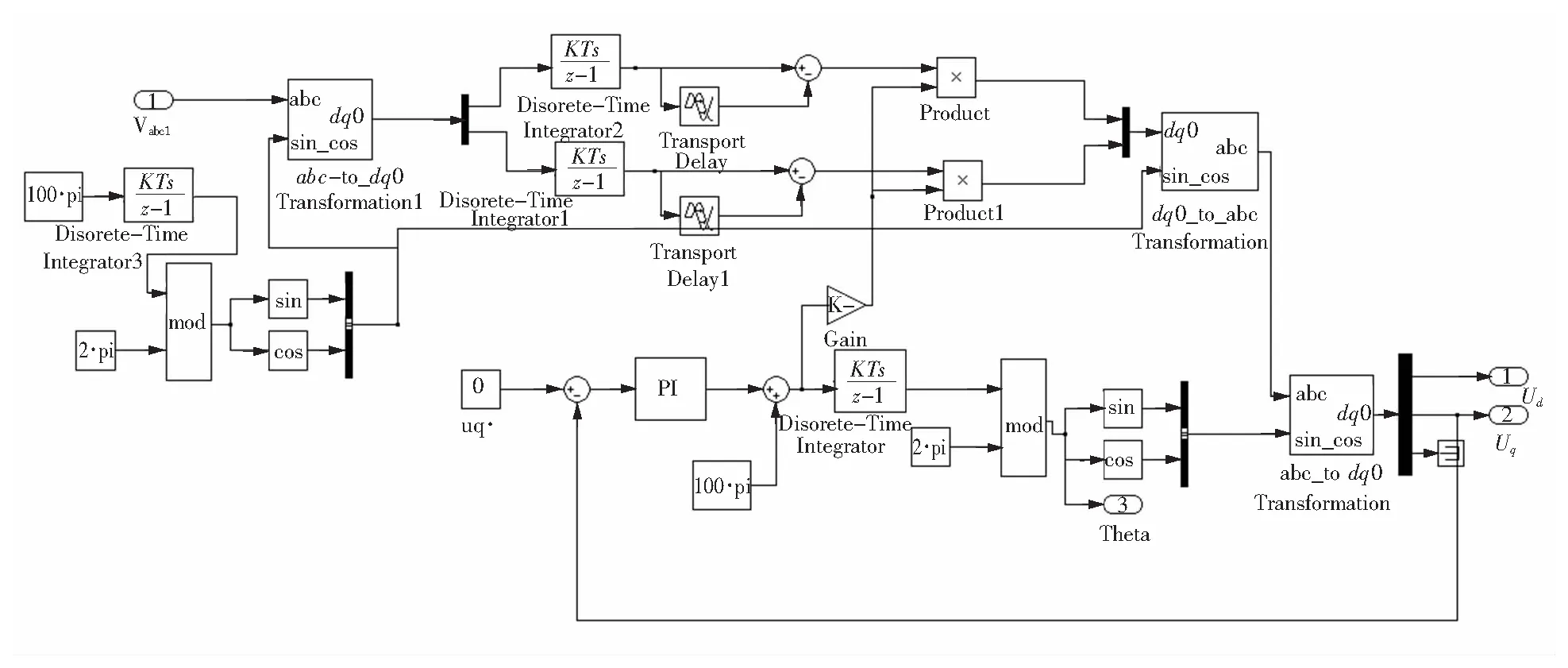
图3 改进锁相环的仿真结构

3.2 电网电压谐波畸变时的仿真

当输入电压信号在t=0.15 s时注入幅值分别为0.1 p.u.,0.1 p.u.的3次和5次谐波，两种电压同步技术的响应如图5所示。

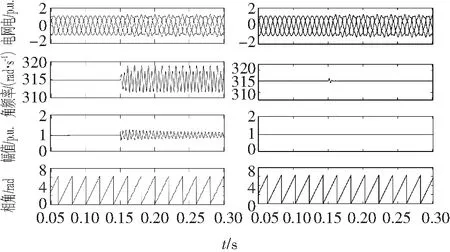
图5 谐波畸变的仿真

由图5知,传统的SRF-PLL锁相信号中也含有谐波,不能准确锁相,基于平均值环节的PLL经过0.01 s后角频率和相位准确锁定。

通过对比图4和图5可以看出,基于平均值环节的锁相环在电网电压不平衡、谐波畸变和频率突变等情况下都能够准确快速锁定电压相位和频率,说明引入平均值环节能滤除输入信号中的负序分量和谐波分量,可以准确获得基波电压信号。与传统的SRF-PLL相比,所提的锁相环通过引入频率反馈环极大地缩短了到达稳态的时间和减小频率的振荡幅度,可以快速准确跟踪电网频率从而实现频率自适应。

4 结 语

针对SRF-PLL在电网电压不平衡时不能消除负序分量和谐波分量的问题,提出了正反dq变换和平均值环节来消除谐波的锁相技术。通过基于任意工频旋转角的正反两次dq变换和平均值环节将系统电压的正序基波分量提取出来,然后再经过dq变换可以准确快速锁定基波正序电压相位。仿真验证了在电网电压畸变和频率突变时,PLL能快速准确地跟踪电网电压频率和相位且频率估计的振荡幅度较小,并具有自适应和抗谐波干扰能力的优点。

[1] 吉正华, 韦芬卿, 杨海英. 基于dq变换的三相软件锁相环设计[J].电力自动化设备, 2011, 31(4): 104-106. JI Zhenghua, WEI Fenqing, YANG Haiying. Three-phase software phase-locked loop based ondqreference frame [J]. Electric Power Automation Equipment, 2011, 31(4): 104-106.

[2] 党克,刘旭阳,吴艳超,等.含多微源的微电网频率综合控制策略研究[J].黑龙江电力,2015,37(1):38-41. DANG Ke, LIU Xuyang, WU Yanchao, et al. Consolidated frequency control strategy of micro-grid containing multiple micro-source [J]. Heilongjiang Electric Power, 2015,37(1):38-41.

[3] 辛业春,李国庆,王尧,等.基于双dq坐标变换的三相电压锁相环的研究[J].电力系统保护与控制,2014,42(10):114-118. XIN Yechun, LI Guoqing, WANG Yao, et al.Research on three phase voltage phase locked loop based on doubledqcoordinate transformation [J]. power system protection and control, 2014,42 (10): 114-118.

[4] 王颢雄,马伟明,肖飞,等. 双dq变换软件锁相环的数学模型研究[J].电工技术学报, 2011, 26(7): 238-242. WANG Haoxiong, MA Weiming, XIAO Fei, et al. Study of model of software phase locked-loop based on dual-dqsynchronous transform [J]. Transactions of China Electrotechnical Society, 2011, 26(7): 238-242.

[5] 邵振华, 陈 冲, 林瑞全. 基于复合二阶广义积分的频率自适应谐波电流检测[J]. 电力自动化设备, 2012, 32(6): 51-55. SHAO Zhenhua, CHEN Chong, LIN Ruiquan. Harmonic current detection with adaptive frequency tracking based on multiple second-order generalized integrators [J]. Electric Power Automation Equipment, 2012, 32(6): 51-55.

[6] 马成斌,杨滔,李春,等.基于二阶广义积分器的正负序锁相环谐波消除方法[J].上海电气技术,2014,7(2):12-17. MA Chengbin, YANG Tao, LI Chun, et al. A harmonic elimination method of positive and negative sequence PLL based on SOGI [J]. Shanghai Electric Tehcnology, 2014,7(2):12-17.

[7] 孔飞飞,袁铁江,晁勤,等.基于二阶广义积分的变流器电网同步法[J].电力系统保护与控制,2012,40(12):116-120. KONG Feifei, YUAN Tiejiang, ZHAO Qin, et al. A method of converter power grid synchronization based on second-order generalized integral [J]. Power System Protection and Control, 2012,40(12):116-120.

[8] 李东,韦统振,霍群海,等.电压畸变条件下软件锁相环精度提高[J].电力电子技术,2011,45(7):95-97. LI Dong, WEI Tongzhen, HUO Qunhai, et al. The improving of soft phase locked loop precision under voltage distortion [J]. Power Electronics, 2011,45(7):95-97.

[9] 范武智,任妍,辛鹤,等.风力发电机组低电压穿越的控制策略[J].黑龙江电力,2014,36(2):107-112. FAN Wuzhi, REN Yan, XIN He, et al. Control strategy for wind turbine low voltage ride through [J]. Heilongjiang Electric Power, 2014,36(2):107-112.

[10] 沈量,尹洪全,李振清,等.一种单相并网逆变器的控制策略的研究[J].东北电力大学学报,2013,33(1):76-79. SHEN Liang, YIN Hongquan, LI Zhenqing, et al. Research on a control strategy for single-phase gird-connected inverter [J]. Journal of Northeast Dianli University, 2013,33(1):76-79.

(责任编辑 郭金光)

Research on phase locked loop based on mean value links under unbalanced and distorted voltage

YAN Binbin1, JIA Jiaoxin2

(1.School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China; 2.School of Electrical and Control Engineering, North China University of Technology, Beijing 100144, China)

The traditional synchronous reference coordinate three phase locked loop(SRF-PLL) failed to accurately track the phase of the grid voltage under the condition of non-ideal grid voltage. To solve this problem, this paper proposed the PLL based on positive and negative dq synchronous reference frame transformation combined with mean value links. It is a method which extracted the positive sequence fundamental voltage through mean value links and used the frequency feedback loop to provide the period of mean value links so as to realize frequency adaptive.The simulation results show that the method is able to realize the positve sequence extraction of fundamental voltage so as to accurately track the phase and frequency of the grid voltage under the condition of unbalanced and seriously distorted three-phase voltage, which verify its validity.

voltage distortion; positive and negativedqsynchronous reference frame transformation; mean value links; phase locked loop

2015-05-11。

闫斌斌(1990—),男,硕士研究生,研究方向为光伏发电技术。

TM761

A

2095-6843(2015)06-0483-04