应用多GPU的可压缩湍流并行计算*

曹文斌，李 桦，谢文佳，张 冉

(国防科技大学航天科学与工程学院，湖南长沙410073)

随着硬件性能的提高及编程技术的改进，图形处理器(Graphical Processing Unit，GPU)加速器在高性能计算领域逐渐得到广泛的应用。在最新公布的超级计算机Top500名单中共有62套系统采用了加速器/协处理器，其中采用GPU加速器有46套，而在最新的Green500名单中前10位的超级计算机均采用了GPU加速器，由此可见GPU加速器在高性能计算中的优势。在通用计算中NVIDA GPU具有低成本、低功耗、高性能及易编程等优点，非常适合计算密集型应用。发布的CUDA并行编程架构［1］使开发人员能够在不了解图形学知识的条件下进行高级语言环境下的GPU编程以高效快速地解决许多复杂计算问题。目前在流体力学领域，已有大量的数值模拟方法针对GPU进行了改造，这其中有计算流体力学(Computational Fluid Dynamics，CFD)、格子玻尔兹曼、直接模拟蒙特卡洛、分子模拟等方法。

湍流一直是CFD领域的难点与热点，近年来，国内外已有许多学者将GPU计算应用到湍流的数值模拟当中，取得了良好的加速效果。Aaron［2］针对不可压缩湍流问题，基于Tesla C1060 GPU发展了大涡模拟求解器并给出了实现多GPU并行计算的方法。Cao与Xu等［3］应用高精度求解器在天河－1A系统上实现了多GPU与多CPU的协同并行计算，讨论了提高异构系统并行效率的方法。Lin等［4］基于GeForce 560Ti GPU发展了多块结构网格湍流求解器，利用MPI加OpenMP实现了多GPU的并行计算。Ali等［5］在Tesla S1070多GPU集群上实现了湍流的直接数值模拟，分析了利用零拷贝技术与固定内存技术对提高系统效率的影响。可以发现，在现有的计算流体力学应用中，大多数研究针对的是计算能力较低的设备。而最新的设备(计算能力3.5)更新了硬件架构，例如引入了Hyper－Q，提升了显存带宽，增加了可用的寄存器个数等，这就需要研究人员根据最新架构的功能与特点对算法做出相应的调整与改进，以发挥设备的最佳性能，实现更加复杂更大计算规模任务的模拟。研究发展了基于CUDA Fortran的三维定常可压缩湍流求解器。

1 控制方程

当不考虑外部加热和彻体力的影响时，三维曲线坐标系下守恒形式的Navier-Stokes方程如下:

此处Q为守恒变量;J代表曲线坐标系(ξ，η，ζ)与笛卡尔坐标系(x，y，z)之间的雅克比转换行列式;F，G，H为曲线坐标系三个方向的无黏通量;Fv，Gv，Hv代表黏性通量。考虑k－ωSST湍流模型时，除了添加两个包含源项的湍流方程之外，方程(1)的形式不变，此时黏性系数μ由层流黏性系数μL及涡黏性系数μT两部分组成，相应的μ/pr关系式如下:

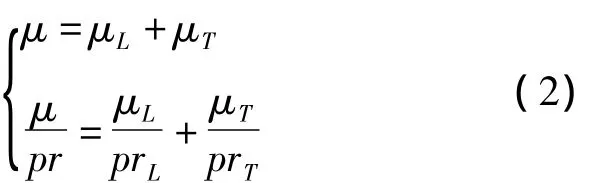
式中，μL通过Sutherland公式得到，μT由湍流模型给出，prL为层流普朗特数，对于空气可取0.72，prT为湍流普朗特数，一般取0.9。当不考虑湍流模型时，涡黏性系数为0。湍流模型的具体公式及参数设置见文献［6］。

对控制方程(1)运用基于单元中心型的有限体积法求解，无黏通量采用AUSMPW+格式［7］，通过MUSCL方法选用Vanleer平均限制器对原始变量进行空间重构达到二阶精度，黏性通量采用高斯积分公式进行求解，时间推进为单步显式方法。

2 GPU算法优化方法

由于GPU程序优化与硬件的体系结构及软件环境密切相关，因此本节首先给出计算平台配置情况。计算软件环境如下:CPU代码用Fortran语言编写，GPU代码为CUDA Fortran语言;两个版本的代码均由PGI Fortran 13.10编译器［8］加OpenMPI库编译，优化参数设置使两种设备的性能达到最佳;GPU计算使用单精度。硬件配置如下:每个节点配置一块CPU与一块GPU及64G内存，节点间通信采用链路汇聚的千兆以太网络;运行的CPU为Intel Xeon E5－2670@2.6 GHz，超线程关闭;测试使用的GPU为6G显存的NVIDA GTX TITAN Black。

2.1 单GPU算法优化

CFD迭代求解过程主要包括边界条件更新、通量计算、时间步长与源项计算及流场更新四个步骤。其中通量计算是决定求解器整体运行速度的主要因素，通常是优化的重点。不管是无黏通量还是黏性通量，在GPU上它们的计算都是首先从全局内存中输入网格单元的几何量和原始变量;其次通过空间格式得到单元界面通量;最后将通量或通量差结果输出至全局内存中。因此从优化方面考虑，可以将通量计算方法分为两类算法:输入优化(算法1)与输出优化(算法2)。为了分析对比，将不进行优化的算法定义为全局内存方法。

算法1的具体流程如下所示。为了节省全局内存开销，界面通量数组f被多次重复使用。

算法1输入优化Alg.1 Input optimization

算法1中每个内核在读取数据阶段，均使用了下面介绍的优化方法。由于每个线程都需要用到相邻线程的信息，例如在计算ξ方向无黏通量Fi－1/2时涉及i－2，i－1，i，i+1共4个网格单元的原始变量值，若应用全局内存方法(将数据从全局内存直接读入寄存器)读取这些信息，将会产生大量的重复访问。为了提高带宽利用率降低访问延迟，常用的办法就是使用共享内存来缓解对全局内存的重复访问，具体使用方法见文献［9］。文献［10］给出了无黏通量计算的一种更高效的方法，即使用寄存器移位技术达到减少重复访问的目的，同时还给出了黏性通量的优化方法。本文求解器在算法1中采用文献［10］的方法进行优化。图1给了大小为1923的网格在不同GPU架构下的通量计算时间对比，与全局内存方法相比，算法1在计算能力2.0的Tesla C2050上获得了25.1%的性能提升，而在计算能力3.5的GTX TITAN Black上仅有8.3%的提升。可以看出，对于重复数据的读取，在显存带宽有了显著提升并引入了L2缓存的计算能力3.5的设备上，使用优化加速技术并不能取得明显的加速效果。

算法2对结果输出做优化，具体的流程如下

算法2输出优化Alg.2 Output optimization

可以看出，算法2在输出阶段利用共享内存消除了中间变量f的使用，这样既节省了全局内存消耗又避免了对全局变量的额外读写操作，同时所有内核不存在数据依赖性可并发执行。因为存储于网格中心的右端项RHS是通过两个界面通量做差值得到，所以每个线程块中计算得到的RHS个数少于线程块中的线程数，这样在每个线程块中除了需要引入新的分支语句，还需要在相邻线程块的边界处进行冗余计算。分支语句的增多与冗余计算的存在使得算法1中的输入优化技术在算法2中不但不能发挥应有的加速效果而且会引起性能的下降。因此算法2在读入数据阶段不进行优化，即应用全局内存方法读取数据。由图1可以看出，算法2非常适合计算能力3.5的GTX TITAN Black，与全局内存方法相比，获得了18%的速度提升。

除了上述优化方法外，一些常规的优化方法在本文中均有应用，如全局变量按数组结构体方式储存，尽量避免束内分支，尽可能减少中间变量以降低寄存器使用量，减少PCIe数据传输，采用树形规约算法执行残值加和操作。所有计算配置的线程块大小为32×8×1。

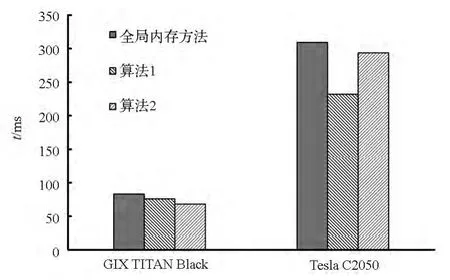
图1 不同算法计算时间对比Fig.1 Computing time of different algorithms

2.2 多GPU并行算法

在求解器进行基于区域分解的并行计算过程中，相邻网格区域在边界处需要对原始变量进行数据交换。当多区网格位于同一块GPU中，此时为内部边界，可以在GPU中实现直接数据交换(求解器支持一个MPI进程处理多区结构网格);当相邻网格区域位于不同GPU时，需要先将一块GPU的边界数据通过PCIe总线传输至主机端，然后调用MPI进行交换，最后再通过PCIe传输至另一块GPU。虽然已有GPUDirect技术实现GPU间的直接通信，但是现有系统的通信设备并不具有该功能，而升级设备成本又很高，因此提高现有系统的并行计算效率具有很大的实用价值。计算能力3.5的GPU引入了一个名为Hyper－Q的重要功能，它允许32个独立的CUDA流队列同时工作。利用该功能，可以实现GPU计算与边界数据交换的高度重叠。具体实现过程如图2所示。

首先，创建N个CUDA流(N≤32)。流1与流2分别用于所有区域的ζ方向内点无黏通量计算与内部边界更新等内核的启动。流3至流N负责所有需要进行数据交换的边界处理，这其中包括GPU上数据整理(将边界数据整理至预先分配好的连续储存空间中)，设备端至主机端的异步传输(Device to Host，D2H)，主机端至设备端的异步传输(Host to Device，H2D)及GPU边界数据更新。其次，所有流启动相应的内核执行，流3至流N的每个流在启动MPI非阻塞发送之前应用CUDA流查询函数确保D2H传输已完成，在启动H2D传输之前需等待MPI非阻塞接受完成。由于Hyper-Q特性允许流与流之间的操作互不阻塞，所以流1与流2对应的多个内核从一开始就与数据整理内核同时启动，内核的执行与PCIe传输及MPI数据交换同步进行，多个D2H或H2D传输可以同时存在，MPI非阻塞通信与D2H传输在不同流之间重叠。最后调用流同步完成所有流的内核执行。图中流1虽然只包含了ζ方向的内点无黏通量计算，若它的计算时间小于数据交换所需要的时间，可以将η方向的相应计算加入流队列中，以实现GPU计算与边界数据交换的高度重叠。

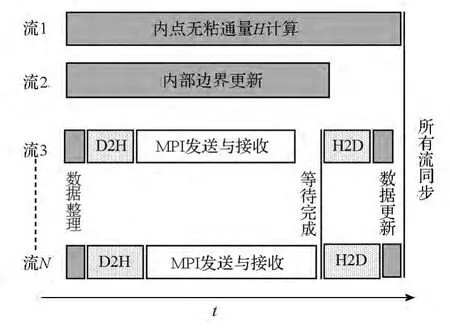
图2 多GPU并行算法Fig.2 Multi-GPU parallel algorithm

3 算例分析

3.1 超声速进气道

Reinartz等［11］对混合压缩进气道进行了大量的数值与实验研究，获得了清晰的流场结构与进气道壁面压力分布。图3所示为扩张段以前的进气道构型，上压缩面的压缩角δ2为21.5°，下楔面的倾斜角δ3为9.5°，扩张段的扩张角δ4为5°，隔离段的长度l为79.3mm，高度h为15mm，进气道总长为400mm，宽为52mm。

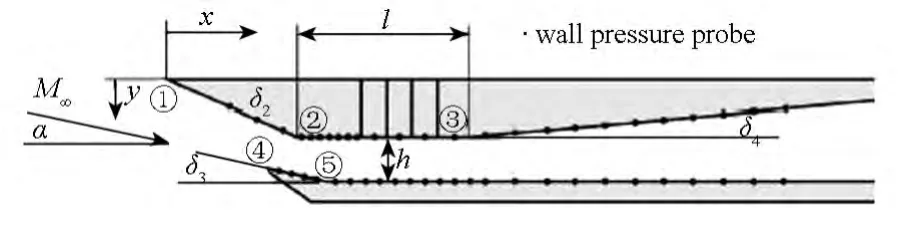
图3 进气道模型示意图Fig.3 Schematic of the inlet model

进气道流动计算条件为:攻角α为－10°，马赫数M∞为2.41，总压540kPa，总温305K。由于实验时间较长，可认为壁面已达到热传导平衡状态，因此计算时壁面采用绝热条件假设。采用单区结构网格对进气道流场区域进行离散。为了测定GPU在不同网格量下的性能表现，设置了多套网格，其中最粗的网格由256×48×64(流向×法向×展向)个网格点组成，在此基础上将前两个方向的网格点数量分别加密得到其余的网格，最密的网格其网格点个数达5033万(2048×384×64)。各套网格均在壁面处进行了加密。

图4 计算得到的密度梯度图Fig.4 Density gradient magnitude of the computation

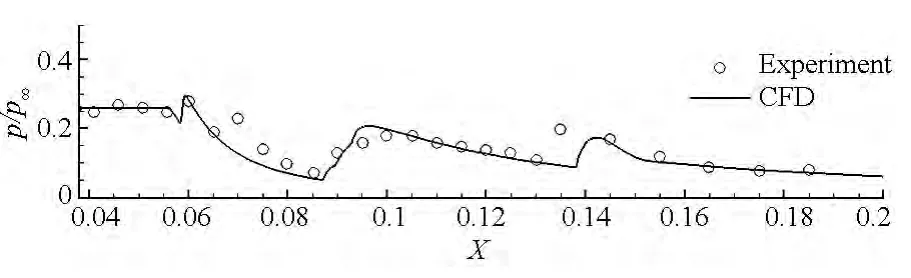
图5 下表面压力分布Fig.5 Lower surface pressure distribution

图4给出了最密网格下湍流模型计算所得到的流场对称面密度梯度云图，可以发现数值计算结果清晰地捕获了进气道内复杂的波系结构。图5给出了进气道下壁面无量纲压力分布计算与实验结果的对比。从图中结果可以看出湍流模型的计算值与实验值在整体分布规律上都比较符合，这表明本文所发展的GPU求解器对可压缩湍流定常问题的模拟是可行的。

图6给出了不同网格下单块GPU与单个CPU核心的计算时间对比及相应的加速比。图中所示的时间为每迭代步所消耗的平均时间，可以看出GPU计算具有明显的速度优势，相对于单个CPU核心而言，随着网格量的增加，GPU的加速比由最初的107倍逐渐增大至125倍。由加速比曲线可发现，小网格量下的加速比明显低于大网格量的情况，即GPU非常适合处理大网格量的计算任务。同时，随着网格量的增加，加速比趋于平缓，这是由于GPU中用于并行计算的CUDA核心数及可并发执行的线程块数是有限的，当CUDA核心的利用率达到饱和时一些线程将会采用串行方式执行，此时加速比将不再增加而趋于稳定。对于不同架构的设备，这个饱和值是不同的，可以看出，当前使用的GPU负载饱和值为500万以上的网格量。

图6 不同网格的计算时间与加速比Fig.6 Computing time and speedup for different grid sizes

并行效率是并行计算必须关注的性能指标。受显存容量的限制，单块GPU所能处理的最大网格量是有限的(对于定常湍流问题，6GB显存至多可处理5000万网格)，考虑到网格规模大小对GPU的性能发挥影响较大，为了真实反映同步与通信开销对并行效率的影响，本文定义并行效率如下:对于某个计算任务，假设它在多块GPU上并行处理的时间为tp，而对每个GPU来说都负载一定数量的网格(单个或多个分区)，设所有GPU单独处理相应的负载所需时间的平均值为ts，则并行效率为ts与tp之比。上述的GPU单独处理既不考虑节点间通信又不考虑节点内通信。对于本算例，每块GPU的负载网格量都相等，且网格拓扑结构简单无节点内通信。表1给出了4块GPU在不同网格量下的计算时间与并行效率，可以看出，较小网格量下GPU的并行效率不高，随着网格量的增加GPU的并行效率逐渐提高。这是因为随着网格量的增加，节点间的通信时间在总的时间中所占比重逐渐减小所以并行效率得到提高。由表中数据可知，应用本文所发展的计算与通信的重叠算法，可使并行效率得到较大提高，相对于无重叠的并行计算，四套网格下内点通量计算与数据传输及通信的重叠可使并行效率提高10%以上。

表1 计算时间与并行效率Tab.1 Computing time and parallel efficiency

3.2 超声速进气道

针对文献［12］所述的空天飞机模型，本文计算了马赫数为4.94，攻角为－5°的实验状态，对应的雷诺数为5.26×107m。空天飞机的长度为0.29m，文献提供了高精度的实验结果。计算方法如前所述，按定常湍流状态考虑，壁面采用绝热条件假设。

图7所示为空天飞机的表面及对称面网格分布，网格总量为1.34亿，共有26个分区，壁面第一层网格高度为1×10－6m。采用4块GPU并行计算，每块GPU负载网格量为3350万左右。图8给出空天飞机的压力及流线分布，因外形复杂，流场中不可避免地会出现激波与激波干扰及流动分离等现象。

图7 空天飞机计算网格Fig.7 Computational grid for the space shuttle

图9给出了机身对称面中心线上表面的压力分布，可以看出，计算结果与实验结果吻合较好，能够反映压力的变化趋势，这说明了求解器对复杂外形模拟具有很好的适应性。

4块GPU并行计算时，每迭代步所消耗的时间为0.667秒，每块GPU单独处理的平均时间为0.611秒，计算得到的并行效率为91.6%，与超声速进气道算例的最高并行效率相比有所降低。这主要是因为单块GPU负载的网格分区过多(尾流场包含18个分区，分配在两个GPU上)引起同步时间消耗增多。此外，负载不平衡也造成了一定的影响，虽然4个GPU所负载的网格量基本相等，但是内部边界及物理边界条件(如壁面条件、远场条件等)更新个数并不相等，分区过多导致了节点内的边界更新操作过多从而影响了整体并行效率。

图8 空天飞机压力云图及空间流线分布Fig.8 Pressure contours and stream lines distribution of the space shuttle

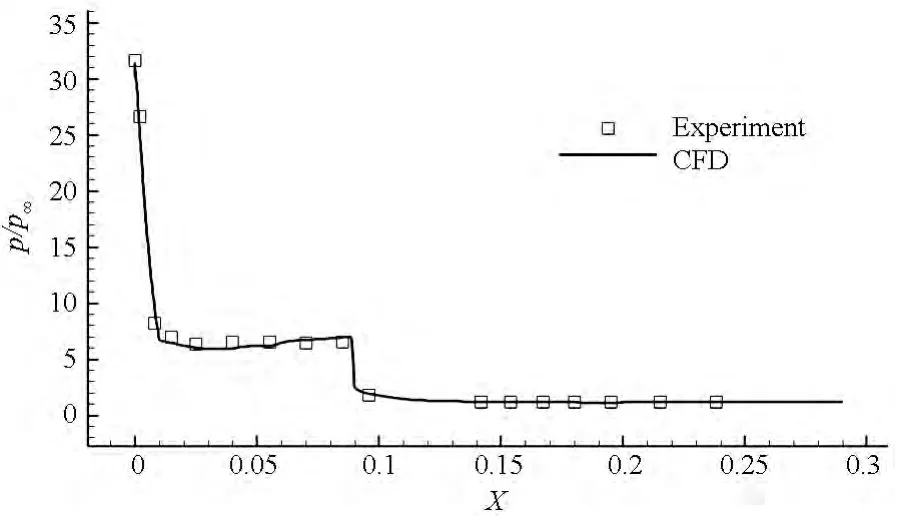
图9 空天飞机对称面上表面的壁面压力分布Fig.9 Pressure coefficient distribution along the upper surface in the symmetry plane

4 结论

本文建立的基于GPU的可压缩湍流求解器，可以快速准确地对超声速流动中的湍流问题进行求解。为了达到良好的加速效果，根据最新的GPU架构特点对GPU程序的算法结构进行了调整与优化，采用两个超声速流动算例验证了GPU求解器的准确性与适应性，实现了多GPU上复杂外形上亿量级网格的快速计算，在最新的GTX TITAN Black GPU上取得了可观的加速比与并行效率。根据研究结果，得出以下结论:

1)不同架构的GPU对应不同的优化算法，对于重复数据的读取，在计算能力3.5的设备上，使用共享内存或寄存器移位等优化加速技术并不能取得明显的加速效果。

2)利用Hyper－Q特性，可以实现GPU计算与PCIe数据传输、MPI通信的高度重叠，能有效掩盖边界交换所带来的时间延迟。

3)从GPU的性能发挥及并行效率方面考虑，GPU负载的网格量应越大越好。对于本文使用的GTX TITAN Black GPU，最佳的负载网格量应在500万以上。

References)

［1］NVIDIA Corporation.NVIDIA CUDA C Programming Guide Version6.5［EB/OL］.［2014－08－01］.http://docs.nvidia.com/cuda/pdf/CUDA-C-Programming-Guide.pdf.

［2］Shinn A F.Large eddy simulations of turbulent flows on graphics processing units:application to film cooling flows［D］.USA:University of Illinois at Urbana Champaign，2011.

［3］Cao W，Xu C F，Wang Z H，et al.CPU/GPU computing for a multi-block structured grid based high-order flow solver on a large heterogeneous system［J］.CLUSTER COMPUT，2014，17(2):255－270.

［4］Fu L，Gao Z H，Xu K，et al.A multi-block viscous flow solver based on GPU parallel methodology［J］.Computers＆Fluids，2014，95:19－39.

［5］Khajeh-Saeed A，Perot J B.Direct numerical simulation of turbulence using GPU accelerated supercomputers［J］.Journal of Computational Physics，2013，235:241－257.

［6］Menter F R.Influence of freestream values on k－ω turbulence model prediction［J］.AIAA Journal，1993，30(6):1657－1659.

［7］Kim K H，Kim C，Rho O H.Methods for the accurate computations of hypersonic flows I.AUSMPW+scheme［J］.Journal of Computational Physics，2001，174(1):38－80.

［8］The Portland Group.CUDA Fortran Programming Guide and Reference Release 2013，version 13.10［EB/OL］.［2013］.http://www.pgroup.com/resources/docs.htm.

［9］Ruetsch G，Fatica M.CUDA fortran for scientists and engineers:best practices for efficient CUDA fortran programming［M］.Holland:Elsevier，2013.

［10］Salvadore F，Bernardini M，Botti M.GPU accelerated flow solver for direct numerical simulation of turbulent flows［J］.Journal of Computational Physics，2013，235:129－142.

［11］Reinartz B U，Herrmann C D，Ballmann J，et al.Aerodynamic performance analysis of a hypersonic inlet isolator using computation and experiment［J］.Journal of Propulsion and Power，2003，19(5):868－875.

［12］李素循.典型外形高超声速流动特性［M］.北京:国防工业出版社，2007.LI Suxun.Hypersonic flow characteristics around typical con Figuration［M］.Beijing:National Defense Industry Press，2007.(in Chinese)