方形截面超高层建筑全风向气动阻尼的试验研究*

李寿英，肖春云，范永钢，陈政清

(湖南大学 风工程试验研究中心，湖南 长沙 410082)

方形截面超高层建筑全风向气动阻尼的试验研究*

李寿英†，肖春云，范永钢，陈政清

(湖南大学 风工程试验研究中心，湖南 长沙 410082)

超高层建筑质量小、阻尼低，极易在设计风速下产生明显的气动弹性效应，出现明显的气动阻尼.考虑一阶线性弯曲模态，制作了方形截面超高层建筑的单自由度气动弹性模型，高宽比8∶1，模型比例1∶600，进行风洞试验测量了各风速下建筑顶部的加速度响应，采用随机减量方法对全风向下方形截面超高层建筑的气动阻尼进行识别.其中，顺风向和横风向的气动阻尼结果与文献结果趋势吻合良好.研究结果表明：当风向角在84°～90°范围内时(90°为横风向)，气动阻尼特性与横风向结果趋势一致；当风向角在0°～12°范围内时(0°为顺风向)，气动阻尼特性与顺风向结果趋势一致；在某些特定的风向角下(例如16.5°)，临界风速降低，气动负阻尼的起始风速也降低.

超高层建筑；气动阻尼；风洞试验；全风向；方形截面

超高层建筑频率低、阻尼小，在风荷载作用下会发生大幅振动，并引起较为明显的气动弹性效应.气动弹性效应可体现为气动质量、气动刚度和气动阻尼.其中，气动刚度和气动质量与高层建筑的刚度和质量相比很小，影响可忽略不计，而气动阻尼的影响则较大.超高层建筑顺风向气动阻尼表现为正阻尼[1-3]，对结构抗风有利，人们常忽略其影响.

很多研究者致力于超高层建筑横风向气动阻尼的研究，通过理论分析[1, 4]和风洞试验[5-7]的手段，研究了结构动力特性(包括结构质量、刚度和阻尼比)[2, 8-9]、湍流度[10]、高宽比和宽厚比[9]、气动措施(如凹角、削角等)[11-12]等对超高层建筑横风向气动阻尼的影响.研究结果表明：方形或矩形截面超高层建筑横风向气动阻尼在折减风速为10左右出现较大的负值[6-7].这与建筑结构的旋涡脱落有密切的关系，因为方形和矩形截面的Strouhal数约为0.1.实际上，不同风向下方形和矩形截面超高层建筑的旋涡脱落特性会有较大的差异，这也将影响超高层建筑的气动阻尼特性，已有文献对全风向下超高层建筑的气动阻尼特性研究较少.本文以方形截面超高层建筑为研究对象，采用风洞试验的研究手段，研究了全风向下方形截面超高层建筑的气动阻尼特性.

1 试验概况

风洞试验在湖南大学HD-2风洞实验室的高速试验段进行，该试验段尺寸为17 m长、3 m宽、2.5 m高，最大风速58 m/s.

1.1 模型参数的确定

选取方形截面高层建筑为研究对象，仅模拟两个弯曲方向的一阶模态.实际建筑高度480 m，截面边长60 m，高宽比为8∶1.实际建筑的密度取为180 kg/m3，结构阻尼比取为1.8%.基频f1可按建筑高度H估算[13]：

f1=1/(0.015H～0.02H)

(1)

这里取f1=0.11 Hz.

模型几何缩尺比Cl为1∶600，密度比Cρ为1∶1.模型高度0.8 m，截面边长0.1 m，最大阻塞率为1.5%，远小于5%，满足风洞测试精度要求.Reynolds数难以在大缩尺比风洞试验中模拟，本试验主要模拟无量纲的Strouhal数，因为结构上的气流分离引起的特征紊流对高层建筑的气动阻尼有很大的影响.Froude数、Cauchy数也不模拟，由于高层建筑主要响应为水平方向，且单自由度气弹模型仅考虑一阶线性弯曲模态，刚度主要通过模型底部的弹簧提供，不模拟Froude数和Cauchy数，影响较小.

在不模拟Froude数的情况下，风速比Cu可直接根据Strouhal数来确定.对于方形截面而言，其涡激共振风速Ust可由下式确定：

(2)式中B为方形截面的边长，B=60 m；St为Strouhal数，对于方形截面，风向与对称轴平行时，可取St=0.10.由此可以得到涡激共振风速为66 m/s，为充分考虑涡激共振对气动阻尼的影响，考虑最大风速为85 m/s.选取风速比Cu为9.5，最大试验风速为9 m/s.由几何缩尺比和风速比，可得频率比Cf为63.16；时间比Ct为1/63.16.

1.2 模型制作

单自由度模型系统的弹性底座包括底部支承支架、万向架、刚度系统、连接件等组成(如图1).万向架(如图1(b))需要满足弹性底座系统沿两个对称轴方向的自由转动，万向架安装在底部支承支架(如图1(a))上，底部支承支架则与风洞转盘中心下的立柱固定.弹性底座系统的刚度由竖向弹簧(如图1(d))提供，弹簧两端分别连接底部支承支架和刚度元件(如图1(c))，刚度元件则与万向架刚性连接.在刚度元件上安装连接件(如图1(e))，以连接弹性底座与高层建筑模型.组装完成的弹性底座系统如图1(f)所示.

高层建筑模型的构造如图2所示，其刚度由直径10 mm、长度600 mm的铝合金芯棒提供，模型底部设置5 mm厚铝合金端板，与铝合金芯棒刚性固定，铝合金端板通过螺丝与弹性底座系统的连接件(如图1(e))连接.模型表面由0.5 mm厚合成材料封闭，内填轻质泡沫.在模型角部预留小孔，以便于加速度传感器引线的布置. 模型安装在风洞实验室中的照片如图3所示.模型结构阻尼比为1.8%，由于本文主要研究风向角的影响，模型装置中没有设置结构阻尼调节装置.

图1 单自由度系统弹性底座示意图

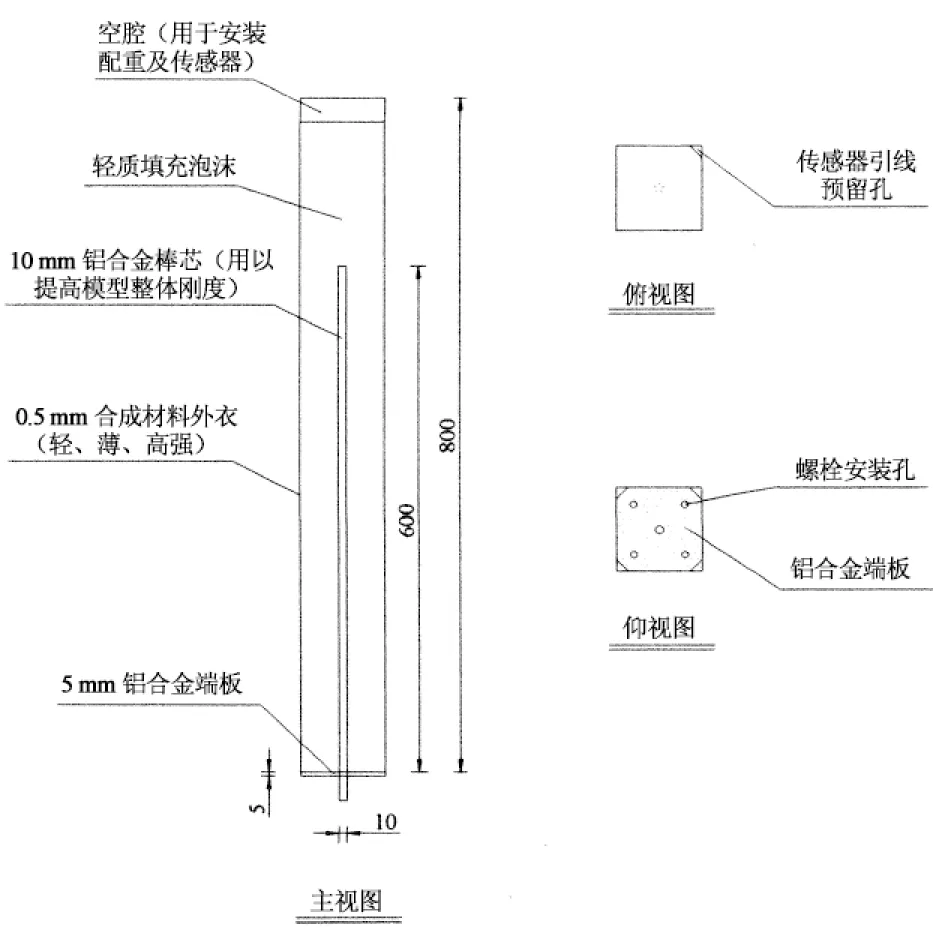
图2 高层建筑模型构造示意图

在线性振型假定的基础上，利用1.1小节的相关参数，可以得到模型的广义质量和广义刚度目标值：

(3)

Km=4π2fm2Mm=915.3 kg/s2

(4)

式中Mm为广义质量；H为模型高度；A为模型横截面面积；Km为广义刚度；fm为模型的频率.需要说明的是，fm通过模型比例、风速比和建筑实际频率f1得到.

图3 模型照片

1.3 风场模拟

试验在B类风场中进行，地面粗糙度指数为0.15，模拟得到的转盘中心处的平均风速剖面、紊流度剖面、顺风向脉动风功率谱如图4所示.

u/u600(a)平均风速剖面和紊流度剖面

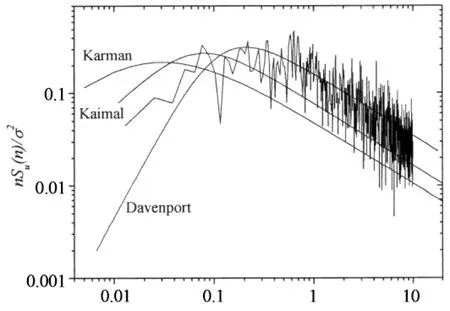
nz/u600(b)顺风向脉动风功率谱

1.4 试验工况

风向角和坐标系定义如图5所示，定义0°方向平行于X轴.由于方形截面具有双轴对称性，进行风洞试验时，仅进行0～45°风向角的气动阻尼测试，即可得到360°风向角下的气动阻尼特性.在建筑顶部设置两个加速度计，具体位置如图5所示，分别测量X轴和Y轴方向的线加速度响应.

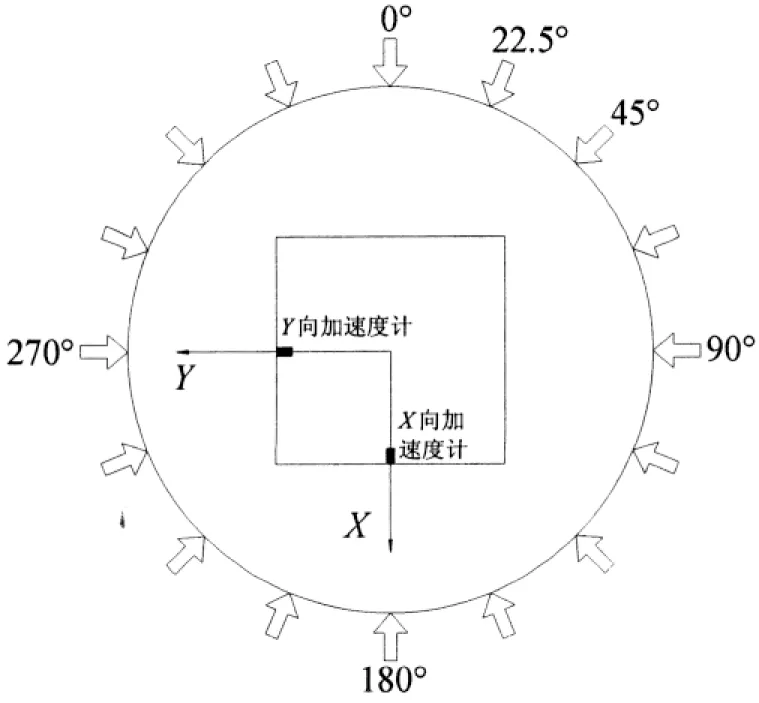
图5 风向角和坐标系定义

选取了α=0°,4.5°,6°,10.5°,12°,16.5°,18°,22.5°,24°,28.5°,30°,34.5°,36°,40.5°,42°和45°共16个风向角进行风洞试验；选取了3,4,5,6,7,8,8.5和9 m/s共8个试验风速，分别对应实际风速的28.5,38,47.5,57,66.5,76,80.8和85.5 m/s共128个工况.对于每个工况，采样时长12 min，对应与实际长度758 min.

2 气动阻尼识别方法

采用随机减量方法识别气动阻尼.随机减量方法的基本思想为：对于在零平均随机过程激励下的系统响应进行多次采样，使采集到的每一样本具有某种共同的初始条件，对采集到的大量样本进行集合平均，可以使响应中的零平均随机量及其造成的影响减小为零，得到初始条件作用下的自由振动响应序列，并从此序列中识别出系统阻尼.

一个单自由度时不变的线性系统在随机外荷载f(t)的激励下的运动微分方程为：

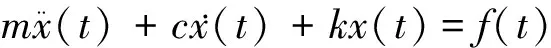
(5)

式中m为系统质量；c为系统阻尼系数；k为系统刚度；x(t)为系统的位移响应.x(t)可以表示为初始位移条件、初始速度条件和外荷载3种因素引起的位移响应的线性叠加：

(6)

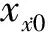
(7)

xx0=th是以xth为初始振幅的自由衰减运动，从中可以方便地识别出阻尼比.在信号长度一定的情况下，截取初始位移值xth越大，有效信号的段数越少，影响平均效果；相反，截取初始位移值xth越小，有效信号段数越多，但激振位移量较小，效果也不理想.本文采用正负阈值同时选取的办法[14]，可适当提高平均效果.图6给出了随机减量方法具体流程图，采用Matlab软件平台，编制了随机减量方法实现程序.以0°风向角、3m/s风速、Y轴方向的原始数据为例(如图7(a)所示)，经过5 000次平均，得到的衰减时程如图7(b)所示.

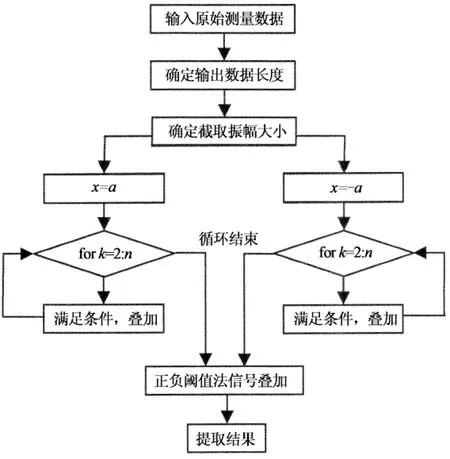
图6 随机减量方法流程图

3 试验结果

图8给出了0°风向角下Y轴(横风向)的气动阻尼比随折减风速的变化规律，同时图8也给出了全涌[7]、Marukawa和Kato等[9]、Watanabe和Isyumov等[10]的结果，以及《建筑结构荷载规范》[15]的规定值.从图8中可以看出，高层建筑横风向气动阻尼在折减风速为10附近出现负值，这主要是因为方形截面的Strouhal数约为0.1，当旋涡脱落的频率与结构频率接近时，结构发生大幅振动，气动弹性效应较为明显，从而产生较大的气动负阻尼.由此可见，高层建筑横风向气动阻尼主要是由涡激共振引起的.比较图8中的4个试验结果，总体变化趋势是一致的，但本文得到的最大正气动阻尼比接近4%，比文献结果大很多，这主要是因为模型结构阻尼比1.8%是在小振幅下测得的，一般来说，结构阻尼比应该与振幅成正比，振幅越大，结构阻尼比越大，因此，大振幅时仍采用小振幅时的结构阻尼比1.8%，低估了结构阻尼比，高估了气动阻尼比.另外，出现气动负阻尼的无量纲风速稍有区别，这主要是由于试验模型(包括高宽比、模型比例)、试验风场、结构阻尼等参数的不一致造成的.总体上来说，本文结果与上述文献结果的总体趋势吻合较好.

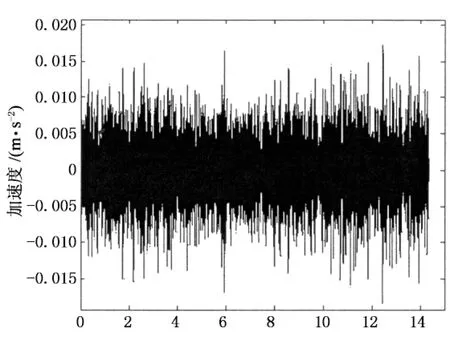
时间/s(a) 原始数据

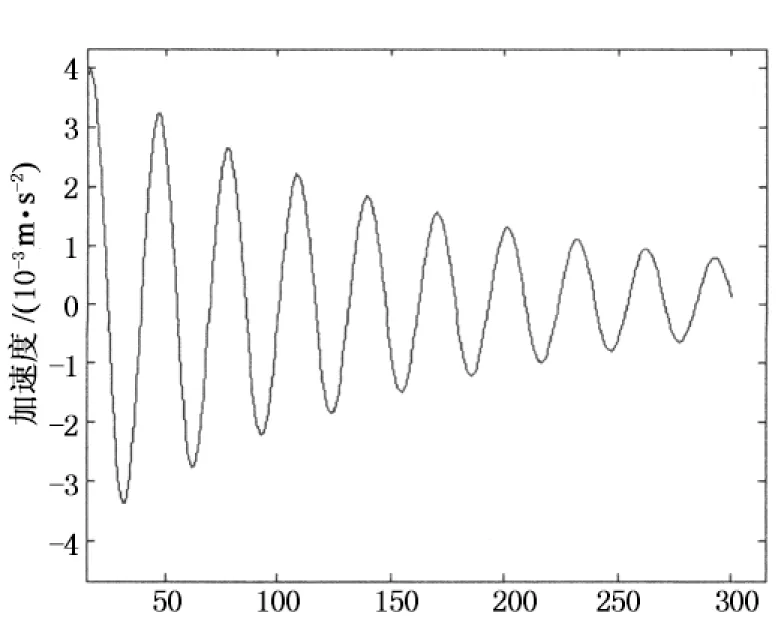
时间/s(b)平均后衰减时程

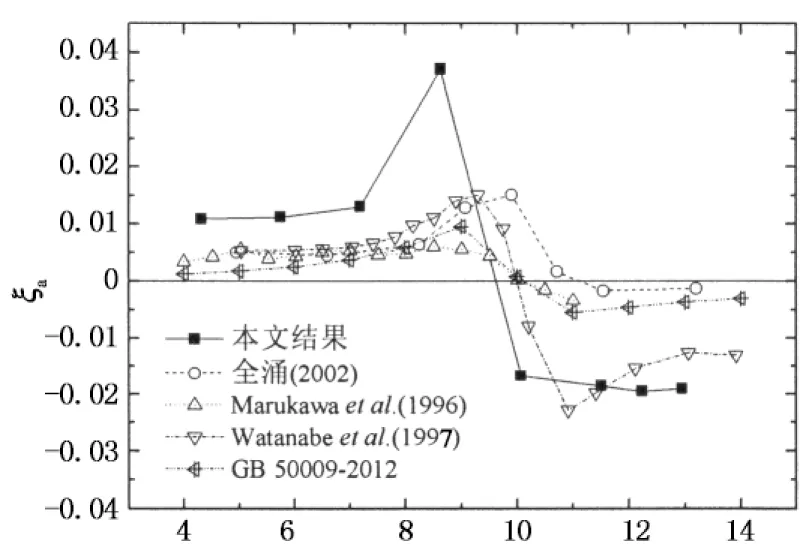
U/(f1B)

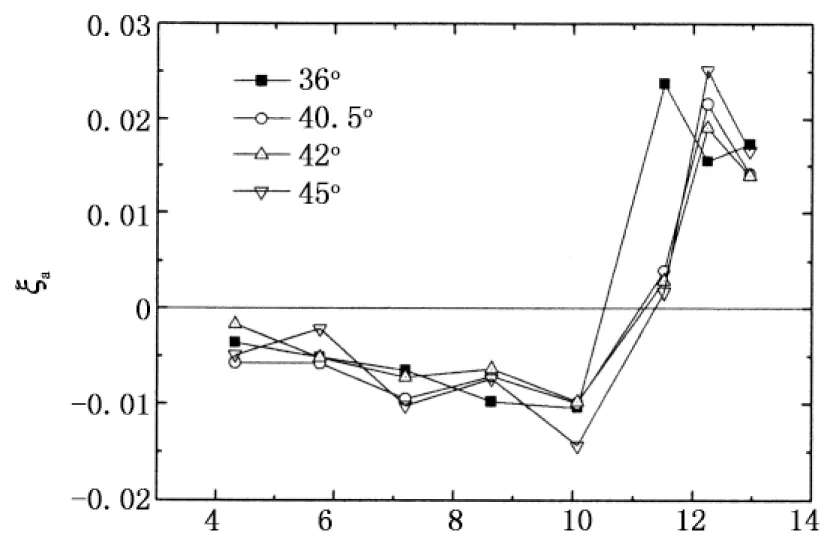
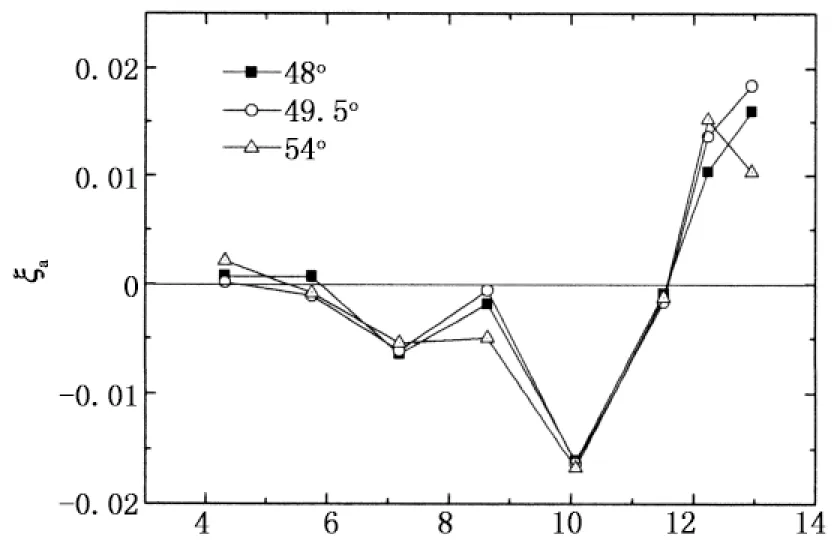
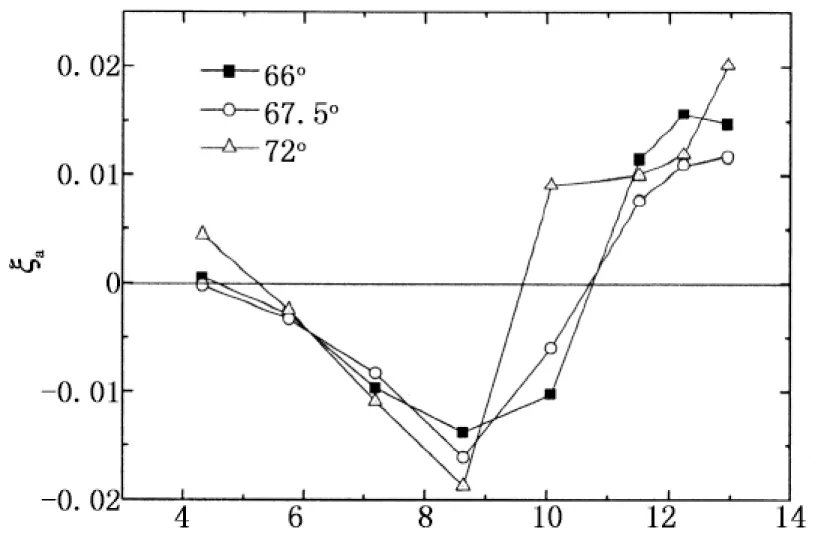
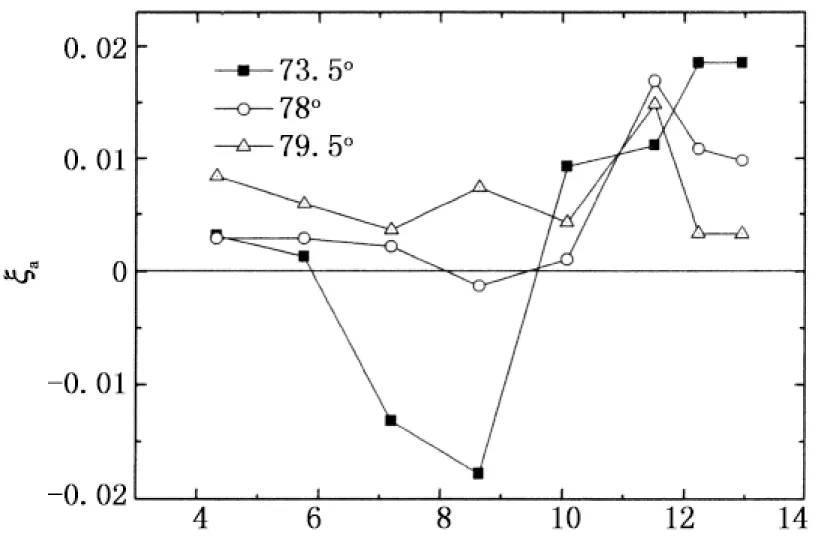
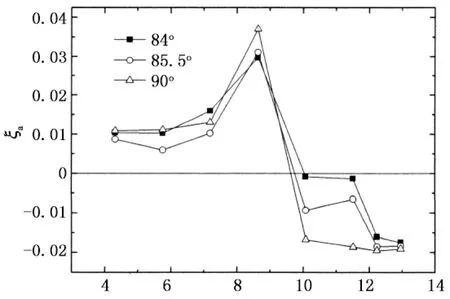
当风向角α=0°～45°，来流与X轴的夹角为α，与Y轴的夹角为90°-α，在后文表述各风向角的气动阻尼结果时，将X轴和Y轴方向的结果合并为X轴，而风向角从0°～45°扩充至0°～90°，也即是说：Y轴风向角α的结果采用X轴风向角90°-α来表示.图9给出了风向角为0°～90°范围内X轴方向的气动阻尼随折减风速的变化规律.从图9中可以看出，风向角为0°～12°范围内时，气动阻尼总体上随风向角的增加而增加，这与高层建筑顺风向气动阻尼的特性基本一致.当风向角达到16.5°时，在折减风速约为7.2附近出现较大的气动负阻尼，临界风速出现减小的趋势.当风向角在18°～45°范围内时，也有较为明显的气动负阻尼，但随着风向角的增加，气动负阻尼减小，临界风速也有所增加.当风向角为48°～61.5°范围内时，气动负阻尼在无量纲风速10左右达到最大.当风向角为66°～73.5°时，气动负阻尼在折减风速8.6时达到最大，而当风向角为78°和79.5°时，气动阻尼基本上呈现正值，与顺风向气动阻尼特性类似.当风向角为84°～90°时，气动阻尼特性与横风向类似，临界风速约为10.

从以上的分析可知，高层建筑的气动阻尼特性与来流风向角有密切关系，这主要是因为不同风向角下的气流分离方式不同引起的.值得注意的是，在某些风向角下，临界风速出现减小的趋势，例如风向角为16.5°、66°～73.5°时，临界风速分别为7.2 m/s和8.6 m/s.另外，出现气动负阻尼的起始风速很低，风向角66°～73.5°范围内最为明显，从折减风速5.7开始气动负阻尼就开始随着风速的增加而增加.气动负阻尼临界风速和起始风速的降低，将导致高层建筑出现气动弹性效应的风速降低，仅根据横风向气动阻尼研究结果可能会导致偏于不安全的判断.

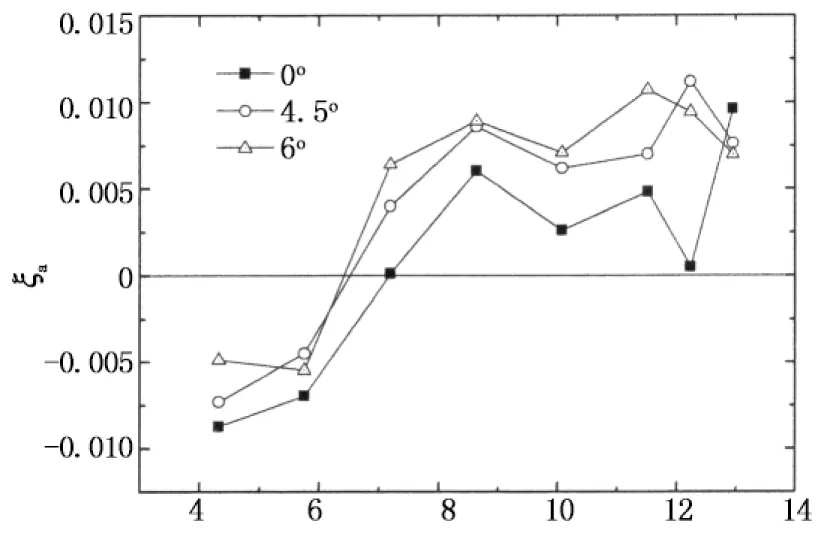
U/(f1B)

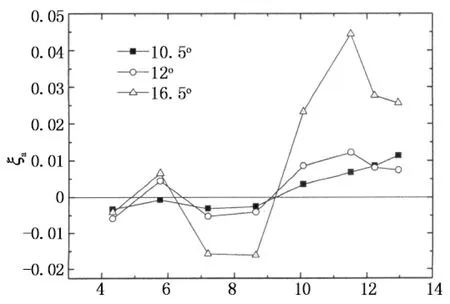
U/(f1B)

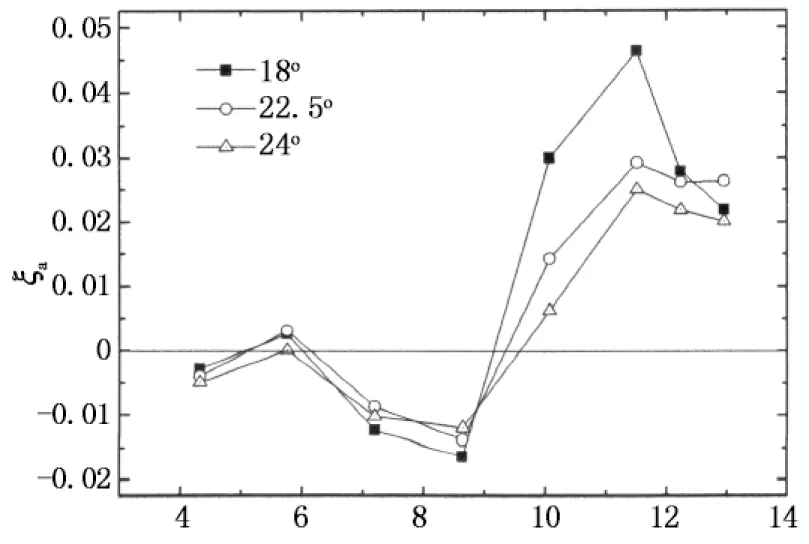
U/(f1B)

U/(f1B)

U/(f1B)

U/(f1B)

U/(f1B)

U/(f1B)

U/(f1B)

U/(f1B)

4 结 论

制作了方形截面超高层建筑单自由度气动弹性模型，并进行了全风向下的气动阻尼的识别，得到如下结论：

1)当风向角在84°～90°范围内时(90°为横风向)，气动阻尼特性与横风向气动阻尼趋势一致；当风向角在0°～12°范围内时(0°为顺风向)，气动阻尼特性与顺风向气动阻尼趋势一致.

2)风向角为16.5°,66°～73.5°范围内时，临界风速分别为7.2 m/s和8.6 m/s，小于横风向气动阻尼的临界风速(约为10.0 m/s)，在研究超高层建筑气动弹性效应时，应考虑这一因素的影响.

3)在风向角为66°～73.5°时，气动负阻尼的起始风速很低，从折减风速5.7 m/s开始，随着风速的增加，气动负阻尼增大.

[1] BOGGS D W.Wind loading and response of tall structures using aerodynamic models[D].Fort Collins:Colorado State University,1991:188-250.

[2] QUAN Y,GU M.Experimental evaluation of aerodynamic damping of square super high-rise buildings[J].Wind and Structures,2005,8(5):309-324.

[3] GABBAI R D,SIMIU E.Aerodynamic damping in the along wind response of tall buildings[J].Journal of Structural Engineering,2010,136(1):117-119.

[4] DAVENPORT A G,TSCHANZ T.The response of tall buildings to wind:effects of wind direction and the direct measurement of dynamic force[C]// Proceedings of the Fourth US National Conference on Wind Engineering Research. Seattle,1981:205-223.

[5] KAREEMA.Wind excited motion of buildings[D].Fort Collin:Colorado State University,1978:23-54.

[6] 曹会兰.基于单自由度气动弹性模型风洞试验的超高层建筑气动阻尼研究[D].上海:同济大学土木工程学院,2012:99-111.

CAO Hui-lan.Aeroelastic experimental study on aerodynamic damping of one degree of freedom super-high-rise buildings[D].Shanghai:College of Civil Engineering,Tongji University,2012:99-111.(In Chinese)

[7] 全涌.超高层建筑横风向风荷载及响应研究[D].上海:同济大学土木工程学院,2002:76-109.

QUAN Yong.Study on across-wind resposnses and static equivalent wind loads of super-high-rise buildings [D].Shanghai:College of Civil Engineering,Tongji University,2002:76-109.(In Chinese)

[8] GU M,QUAN Y.Across-wind loads of typical tall buildings[J].Journal of Wind Engineering and Industrial Aerodynamics,2004,92(13):1147-1165.

[9] MARUKAWA H,KATO N,FUJII K,etal.Experimental evaluation of aerodynamic damping of tall buildings[J].Journal of Wind Engineering and Industrial Aerodynamics,1996,59(2): 177-190.

[10]WATANABE Y,ISYUMOV N,DAVENPORT A G.Empirical aerodynamic damping function for tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72(97):313-321.

[11]DAVENPORT A G.The response of super tall buildings to wind[C]// Second Century of the Skyscraper. 1998:705-725.

[12]KIM Y M,YOU K P,KO N H.Across-wind responses of an aeroelastic tapered tall building[J].Journal of Wind Engineering and Indu-strial Aerodynamics,2008,96(8): 1307-1319.

[13]TAMURA Y,SUDA K,SASAKI A.Damping in buildings for wind resistant design[C]// Proceedings of the International Sym Posium on Wind and Structures for the 21st Century.Chenju,1999:115-129.

[14]张西宁,屈梁生.一种改进的随机减量信号提取方法[J].西安交通大学学报,2000,34(1):106-110.

ZHANG Xi-ning,QU Liang-sheng,Improved method for extracting of random decrement signal[J].Journal of Xi'an Jiaotong University,2000,34(1):106-110.(In Chinese)

[15]GB50009-2012 建筑结构荷载规范[S].北京:中国建筑工业出版社,2012:51-54.

GB50009-2012 Load code for the design of building structures [S].Beijing: China Building Industry Press,2012:51-54.(In Chinese)

Experimental Investigation of Aerodynamic Damping on Super-high-rise Buildings with Square Cross Section under the Action of Full-direction Wind

LI Shou-ying†, XIAO Chun-yun,FAN Yong-gang, CHEN Zheng-qing

(Wind Engineering Research Center, Hunan Univ, Changsha, Hunan 410082,China)

Super-high-rise buildings experience aeroelastic effects under the action of design wind velocity for its low mass and structural damping, and significant aerodynamic damping arises. Considering the first order linear sway mode, a single degree-of-freedom aeroelastic model of super-high-rise buildings with square cross section was made with a geometrical scale of 1∶600, and a series of wind tunnel tests were carried out to measure the accelerations on the top of the building model. Random Decrement Technique (RDT) was adopted to identify the aerodynamic damping of the building model. The aerodynamic damping in along-wind and across-wind directions obtained agrees well with that from literatures. The results show that the aerodynamic damping within the wind direction of 84°～90° is similar to that in the across-wind direction (90°), and the aerodynamic damping within the wind direction of 0°～12° is similar to that in the along-wind direction (0°). It should be noted that critical wind velocity decreases under some special wind directions, such as a reduced wind velocity of 7.2 in wind direction of 16.5°. Moreover, negative aerodynamic damping is found at low wind velocities.

super-high-rise buildings; aerodynamic damping; wind tunnel tests; full-direction wind; square cross section

1674-2974(2015)07-0009-07

2014-10-29

湖南省高校创新平台开放基金资助项目(湘教通(2012)595)；国家重点基础研究发展计划项目(2015CB057701,2015CB057702)

李寿英(1977-)，男，江西萍乡人，湖南大学副教授，博士，博士生导师

†通讯联系人，E-mail:shyli@hnu.edu.cn

TU973.3

A