考虑流固耦合的近海风机动力响应数值计算*
邓 露,肖志颖,黄民希,宋晓萍,吴海涛
(1.湖南大学 土木工程学院,湖南 长沙 410082; 2. 湘电风能有限公司,湖南 湘潭 411102)
考虑流固耦合的近海风机动力响应数值计算*
邓 露1†,肖志颖1,黄民希1,宋晓萍2,吴海涛2
(1.湖南大学 土木工程学院,湖南 长沙 410082; 2. 湘电风能有限公司,湖南 湘潭 411102)
研究了固定式海上风机的流固耦合问题.选取美国可再生能源实验室(NREL)建立的5 MW海上单桩式风机模型,采用Kaimal谱和风剪切指数理论模型,通过NREL编写的程序—TurbSim,生成脉动风场,进而使用气弹程序FAST计算风力机的气动荷载,输出包括剪力和弯矩在内的塔顶荷载时程.选取Pierson-Moskowits波浪谱,并利用谐波叠加法模拟随机波浪.采用Morison公式计算波浪力,分别建立了海上风机塔架考虑与不考虑流固耦合效应时的动力方程及数值模拟方法,并对比分析了这两种情况下的波浪力和结构响应的差异.结果表明,两种情况下计算得到的波浪力和风机响应有明显差异,并且这种差别跟风浪大小等因素有关.
海上风机;随机风浪;流固耦合;Morison方程
在海洋工程中,小尺度(直径相对于波长较小)圆柱结构应用相当广泛,且波浪荷载是其设计的控制荷载.因此,研究波浪荷载对此类结构物的作用具有重要的工程意义.1950年Morison[1]等提出了一个计算小尺度结构所受波浪力的经验公式,该公式形式简单,能够满足一般工程需要,至今仍广泛使用.但当结构本身的振动较大时,结构的运动会改变波浪力的大小,结构与波浪之间的流固耦合效应不能忽略.Sarpkaya[2]等人针对这一问题将Morison方程进行了修改,提出了考虑相对运动的修正Morison方程.Fish[3]等人针对修正Morison方程中的流固耦合问题进行了试验和理论研究,提出了相应的简化计算方法.国内方面,王元战[4]等研究了离岸深水码头桩基所受波浪力的流固耦合问题;徐亚洲[5]等提出了一阶预估校正法来研究结构流固耦合波浪动力响应.
对于深海结构物,结构的柔度较大,其自身运动对波浪的影响较大.因此,计算波浪力时应该考虑结构自身的运动,即流固耦合问题.比如Chandrasekaran[6]等应用修正Morison方程进行深海结构的波浪力计算,采用Monte-Carlo方法模拟随机波浪荷载,研究了张拉腿平台结构在随机波浪作用下的结构响应.而对于近海结构物,结构刚度较大,计算波浪力时一般不考虑流固耦合.
然而,修正前和修正后的Morison公式两者的应用范围并没有明确的界限.对于固定式海上风机结构,计算其所受的波浪力时可按DNV[7]规范的规定不考虑流固耦合.Shirzadeh[8]等对比研究了评估海上风机阻尼的实验和数值方法,计算波浪力时没有考虑流固耦合.但是也有学者考虑了流固耦合:Agarwal[9]等研究海上风机aero-servo-hydro-elastic(空气动力-水动力-伺服)耦合模型时,考虑了流固耦合问题计算不规则波浪力;李德源[10]等研究了固定式海上风力机塔架在随机风、浪载荷作用下的动力响应,考虑了流固耦合问题计算不规则波浪力.张学志[11]等人对海洋平台的流固耦合问题进行了相关研究,发现是否考虑流固耦合对结构的位移和加速度等响应有较大影响,但其研究对象没有涉及海上风机.
海上风机结构在振动控制方面有较高要求,振动过大会对风机造成损害,导致运行故障.GL[12]风机认证规范专门规定了振动限值.因此准确计算风机结构的动力响应不仅能够指导工程设计,亦能对风机工作性能进行准确评估.由于风机自身结构高耸,且受到风浪流等多种复杂荷载作用,其结构的力学特性与海洋平台、浮式风机有较大差异,是否需要考虑流固耦合问题,以及流固耦合问题对计算波浪荷载和结构的动力响应的影响程度,都值得深入研究.
针对上述问题,本文对比分析了固定式海上风机结构考虑与不考虑流固耦合问题的波浪力计算方法,并分别建立了两种情况下的海上风机塔架动力方程及有限元数值模拟方法,以此探究海上风机波浪力计算中的流固耦合问题.并以NREL-5 MW(5兆瓦)风机模型为算例,对比分析了计算结果的差异,获得了一些对工程实践有意义的结论.
1 理论介绍
1.1 风机模型
固定式海上风机主要由基础、塔架、发电机组构成.本文采用Ansys软件建立有限元模型,将机舱和叶片等效成为塔顶的质点;用梁单元模拟塔架以及基础结构;为简化计算,将基底边界条件假设为固接.风机结构受到的随机风荷载和随机波浪荷载作用在相应的质点.风机模型图如图1所示.
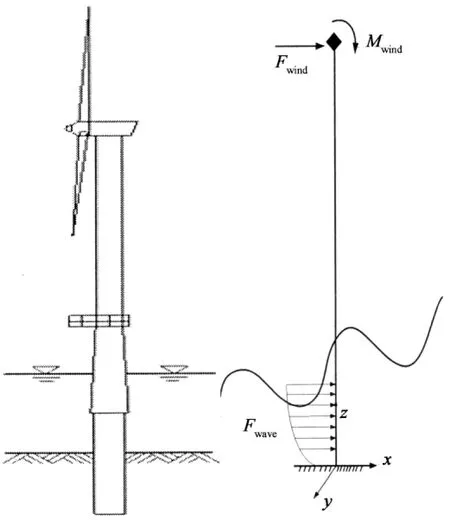
图1 风机模型图
1.2 风机结构动力学方程
本文计算风机x方向的动力响应,其动力学方程如下:

[Fwave]+[Fwind]
(1)
式中[M],[C]和[K]分别为风机结构的质量矩阵、阻尼矩阵和刚度矩阵;[Fwave],[Fwind]分别为波浪荷载和风荷载.[C]采用Rayleigh阻尼,计算公式如(2)~(4)所示.动力学方程求解采用Newmark-β法求解,利用自编Matlab程序计算.
(2)
(3)
(4)
式中α1,β1为比例系数;ω1,ω2分别为第一、第二阶自振频率(rad);ζ1,ζ2为对应的阻尼比.
1.3 波浪荷载模拟
1.3.1 随机波浪模型
海上风机结构承受多种复杂荷载,其中波浪荷载是风机塔架的主要设计荷载[13].工程上有多种方法描述波浪,比如Stokes波理论、流函数理论等.由于海浪具有随机性, 设计过程中必须考虑结构响应的随机性.因此,本文采用随机波浪理论描述波浪.工程上一般采用Jonswap,Neumann或Pierson-Moskowits[14]等谱来模拟随机波浪.首先,根据近海风电场的风况和波候等条件得到海浪的统计参数,如有效波高、跨零周期等,以产生波浪的功率谱密度信号,然后利用谐波叠加法得出波高的时域信号,最后选取合适的波浪理论得到水质点的速度、加速度等运动参数.本文采用Pierson-Moskowits谱(简称P-M谱)进行计算,具体表达式如下:
(5)
式中Sη(ω)为波浪谱密度函数;ω为波浪频率(rad);α2,β2为常数,α2=0.008 1,β2=0.74;U为海面以上19.5 m的风速(m/s);g为重力加速度(m/s2).
此波浪谱公式含有风速项,说明其蕴含了风浪之间的关系,即确定风速后就可以确定波浪谱信息.根据设计资料,可以确定式(5)中的具体参数,代入公式后,即可以得到能量谱分布,典型P-M谱函数曲线如图2所示.
随机波浪理论[15]将波浪视为由无限多个振幅不等、频率不等、初相位随机的余弦波叠加而成,利用谐波叠加法得到波高,理论计算公式如下:
(6)
式中η(t)为波高函数;t为时间;εn为0~2π之间均匀分布的初相位.

ω/rad
为进行数值计算,将自变量波浪频率平均分成N个区间,每个区间长度为Δωn,用区间边界的平均值作为该区间的代表值ωn,即可用数值计算公式(7)得到波高.
(7)
计算得到的典型波高时程曲线如图3所示.
t/s
假设流体为无粘性不可压缩的均匀流体,采用airy线性波浪理论来求解波浪.目前工程上随机波的模拟都是基于线性波来模拟的,即Longuet-Higgins随机波浪模型,这样可得到波浪的速度、加速度等运动特性.airy波浪理论的计算公式表述如下.
波浪弥散关系:
ωn2=gkntanhknd
(8)
波浪速度场:


(9)
加速度场:


(10)
式中Hn为波高;Tn为波浪周期;d为水深;kn为波数;z为质点z方向坐标.通过式(9),(10),可以得到相关质点波浪运动参数.
1.3.2 随机波浪荷载
在得到波浪速度、加速度之后,即可计算海上风机的波浪荷载.采用Morison公式,将水平波浪荷载分为水平惯性力和水平拖拽力,当结构振动比较小时,风机任意质点波浪力计算公式如下:
(11)
式中fD为拖拽力;fI为惯性力;CD为拖拽力系数;CM为惯性力系数;ρ为海水密度;V0为单位柱体高度的排水体积.
当考虑流固耦合时,结构质点波浪力计算为:
(12)
将式(12)代入式(1),得到质点动力学方程:
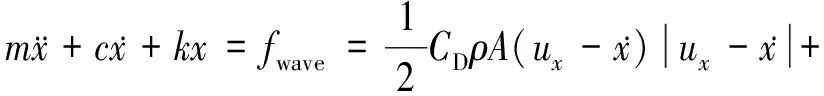

(13)

(14)
不难发现方程(14)等号右边的波浪力项与方程(11)是一致的.考虑耦合的时候,只需要将质量矩阵相应的自由度加上一个附加质量系数即可,相对于张学志[11]等人的方法,计算相对简单.最后将计算出风机塔架的速度,加速度代入式(12)就可以得到考虑流固耦合情况时的波浪力.
1.4 风荷载模拟
1.4.1 随机风模型
风场中任一点的风速可分为两部分:平均风速和脉动风速.前者需考虑在大气边界层范围内的风剪切效应来模拟平均风速随高度的变化;后者可视为零均值、平稳各态历经的随机过程,根据功率谱函数进行数值模拟.
风剪切模型有对数和指数模型,分别假定风速随高度呈对数和指数变化.常用的脉动风功率谱有Kaimal谱、Von Karman谱等.在模拟空间网格上每点的脉动风速时间历程时,必须考虑到这些时间历程是相干的,且这种相关性随着距离的增大而减小,在高频时比低频小,用相干函数来描述这种关系.
通过NREL开发的前处理程序——TurbSim生成风速场.该程序能够根据不同的参数生成三维、随机的湍流风速场.选用指数模型考虑风剪切效应:
(15)

在TurbSim中选用IEC61400-1中的Kaimal谱[16],计算公式如下:
(16)
根据IEC61400-1标准,模拟正常湍流风况;选用该标准的相干方程考虑纵向风速u的相关性:
(17)
但该标准没有定义横向风速v和垂向风速w的相干模型,故在选用了IEC标准的前提下,TurbSim不考虑横向和垂向风速的相干性.
1.4.2 随机风荷载计算
基于随机三维全域风场计算轴向和切向诱导因子在叶片上的分布,从而得到诱导速度,进而求解叶片所经历的风速及攻角.图4为风轮平面内的速度.
常用计算诱导速度的理论有叶素动量理论(BEM)和动态尾流理论(GDW).动态尾流理论是基于拉普拉斯方程的势流解,相比于叶素动量理论,能够考虑转子平面上的更广义的压力分布,且能模拟流经叶片的风速变化时叶片受到的气动载荷变化的时间滞后效应.在此基础上,利用由风洞实验或者CFD计算获得的翼型空气动力学参数,包括升、阻力系数与攻角的关系和动态失速参数,最终计算作用在叶轮上的气动荷载.局部的升力和阻力按如下公式计算:
(18)
(19)
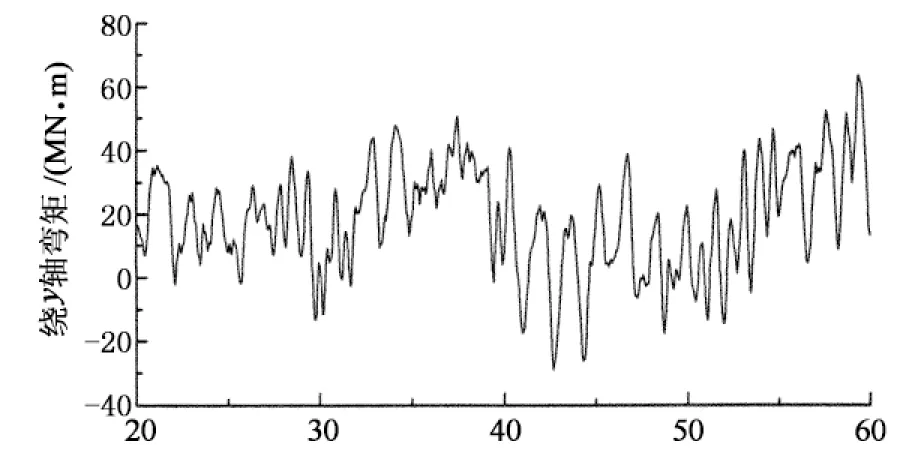
采用NREL开发的程序——FAST计算叶轮上的气动荷载,在该程序的气动荷载计算子模块AeroDyn对应的输入参数中,选用Peters与He[17]提出的动态尾流模型来计算诱导速度.在FAST的输入文件中,需要配置好所用到的翼型数据文件,每个翼型数据文件中包含了在±180°范围内的攻角所对应的升力系数 、阻力系数和变桨系数.表1为DU系列和NACA系列翼型族的叶素参数.由于风剪切、偏航和湍流等因素,叶片将不可避免地出现动态失速效应,故在AeroDyn中采用Leishman和Beddoes[18]提出的半经验模型动态失速模型,并在翼型数据文件中配置好动态失速参数.最后输出3个方向的剪力和弯矩时程,将风荷载作用在风机塔顶节点.图5和图6分别为较大风浪时塔顶x方向剪力和绕y轴弯矩的时程图.

图4 风轮平面内的速度
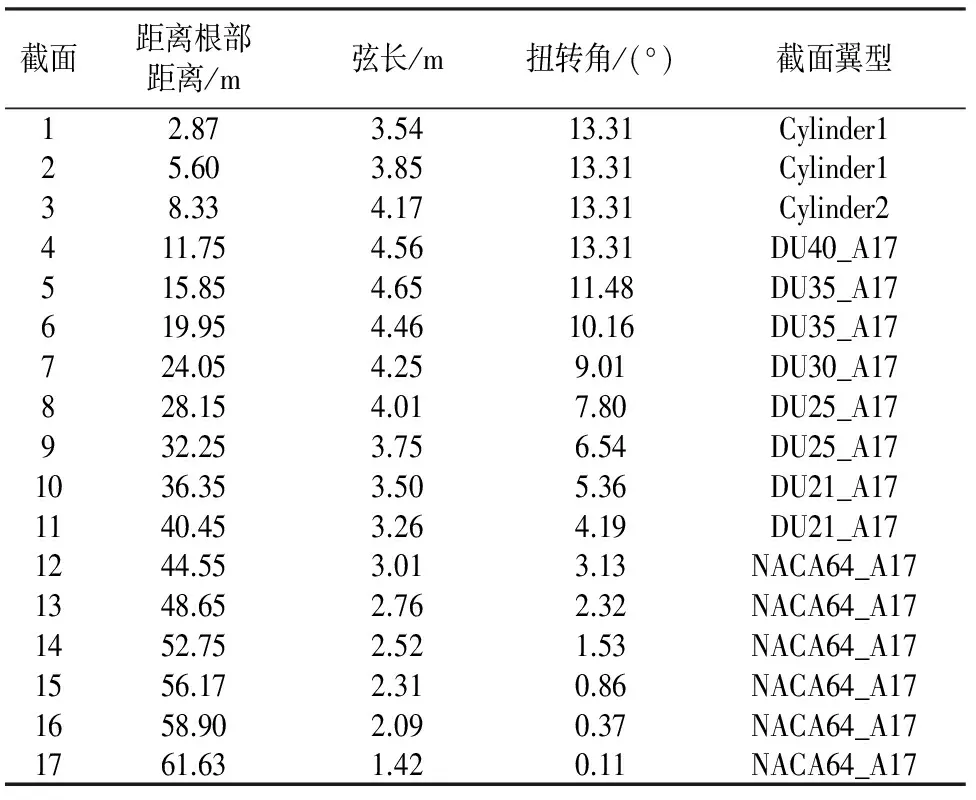
表1 叶素参数

时间/s
时间/s
2 算 例
2.1 单桩式基础海上风机
本文使用美国可再生能源实验室(NREL)建立的5 MW海上单桩风机模型进行分析,该模型整体参数见表2[19].桩顶高出海底30 m,塔架安装在桩顶.塔架呈锥形,顶部直径3.87 m,壁厚0.019 m,底部直径6 m,壁厚0.027 m.单桩呈圆柱形,直径6 m,壁厚0.06 m.
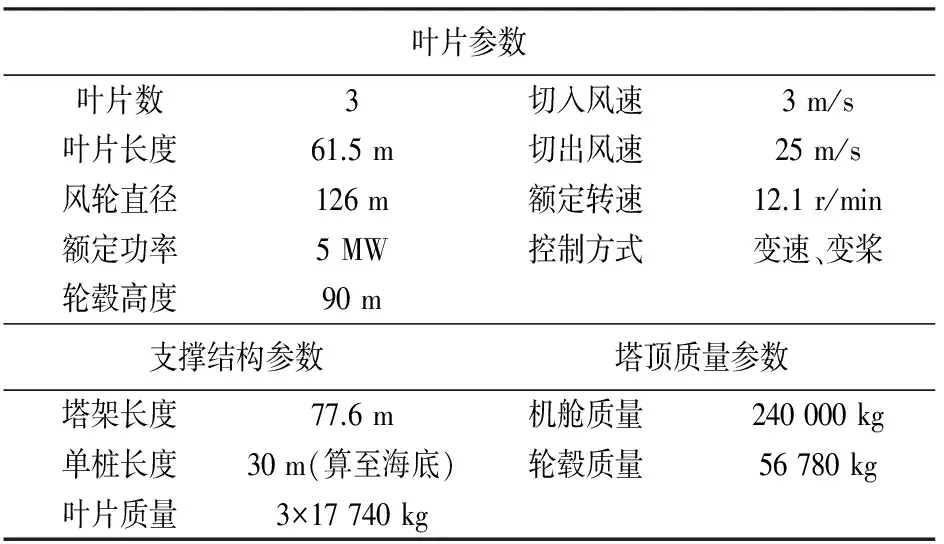
表2 风机总体参数
2.2 计算工况
本文选取5 WM风机模型,以水深、风浪大小、波高影响为变量,计算了24种组合工况.如表3所示.

表3 计算工况
其中“风浪大小”可以用轮毂风速控制,选取不同的轮毂风速,然后可以根据式(16)得到海上19.5 m处的风速,继而代入P-M谱公式(5)就可以得到波浪参数.3个取值分别代表了“较小风浪”、“中等风浪”和“较大风浪”.
为了计算方便,工程上通常将波浪力从海底计算到静水面.但是对于浅水区非线性波浪, 这种取法可能产生较大的误差,因此也有学者将其从海底计算到自由波面.为了考虑波面变化对流固耦合问题的影响,将其作为一个自变量,不考虑其影响时,将任意时刻波浪力从海底计算到静水面,考虑其影响时,将任意时刻波浪力从海底计算到自由波面.本文是按照线性外延法考虑自由液面的影响,即把线性波理论延伸到自由液面.波浪质点速度的修正采用Chakrabarti[20]提出的等效水深方法,具体计算公式如下:
(20)
式中H为波高;T为波浪周期;d为水深;k为波数;z为质点z方向的坐标;η为波高.
2.3 计算结果
为进行分析,定义相对误差δ的计算公式:
(21)
式中Max可为波浪力、结构位移或加速度最大值.
对于波浪力,在所有工况的计算结果中,考虑耦合与不考虑耦合计算结果的差别较大.图7为工况“d=35 m,较大风浪,考虑波面影响”时,结构上z=30 m处的质点所受波浪力时程图.当发生最大值时,计算两种情况的相对误差值,所有工况中的最大相对误差达到41.7%.将图7所示波浪力进行频谱分析发现考虑流固耦合时,波浪力出现了高频的成分,而不考虑耦合时波浪力没有高频成分,如图8所示.
为研究高频成分出现的原因,对结构进行模态分析.考虑到结构的截面是xy平面的圆形截面,其在x和y方向振动的模态相同.本文研究的是结构x方向运动,只需要研究第1,4阶模态,第2,3阶是与1,4阶对应的y方向振动,如图9所示.可以发现波浪力中的高频成分与结构自振频率基本吻合.

t/s

频率/Hz

图9 第1,4阶振型图
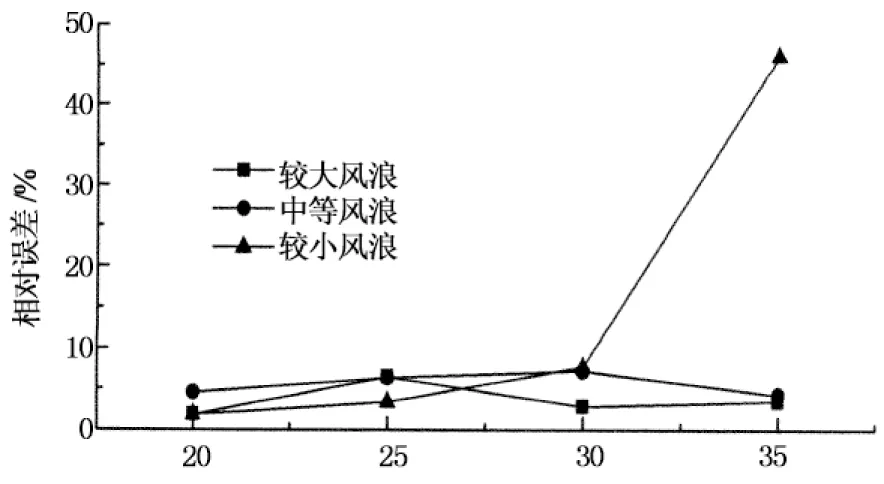
为了研究波浪力的差别与波面因素的关系,计算所有质点的总波浪力,在结果中发现波面因素对波浪力的影响较大.比如在工况“水深20 m,中等风浪”中,考虑波面影响时的波浪力峰值较不考虑时大47.1%,所以计算波浪力时,建议考虑波面因素的影响,并且波浪力峰值的差别随水深加大而变大.图10为考虑波面影响时,水面以下5 m处质点波浪力峰值相对误差与水深的关系图,图11为波浪合力的峰值相对误差与水深的关系图.从图10和图11能看出,在“风浪较小”时的波浪力相对误差较大,这是由于考虑了风机变浆的缘故.在一定范围内,随着风速的增大,虽然波浪荷载变大但风荷载反而变小,导致“风浪较小”的情况下波浪力的相对误差较大,由此推断风浪大小对波浪力有一定的影响.

水深/m
水深/m
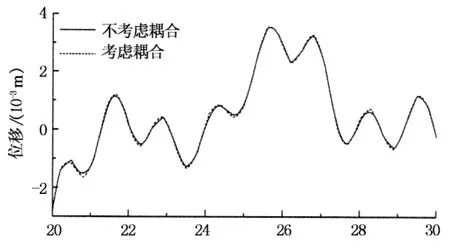
对于动力响应的差别,在所有工况的计算结果中,考虑耦合与不考虑耦合计算的位移、速度的差别较小,而加速度差别较大.所有工况中,塔顶位移最大相对误差为7.6%,塔顶速度最大相对误差为4.6%,而塔顶加速度最大相对误差为35.5%.图12~14为工况“d=35 m,较大风浪,考虑波面影响”时,塔顶处的动力响应时程图.并且最大加速度相对误差值跟风浪和水深也有一定的关系.图15为考虑波面影响时,最大加速度相对误差与风浪、水深的关系图.
时间/s

时间/s

时间/m

水深/m
3 结 论
本文研究了固定式海上风机的流固耦合问题,分别建立了海上风机塔架考虑与不考虑流固耦合效应时的动力方程及数值模拟方法.计算结果表明:
1)考虑流固耦合问题时比不考虑流固耦合时计算的风机波浪力峰值较大,并且从频谱分析可以发现:考虑流固耦合时波浪力会出现高频的成分,波浪力高频的成分可能引起结构高频振动.并且,波浪力峰值差别的大小随水深加大而变大,且与风浪大小有一定关系.此外,计算波浪力时应该考虑波面的影响,并需要综合考虑风浪大小.
2)对比考虑和不考虑流固耦合对风机塔架动力响应的影响时发现,两者情况下获得的位移和速度的差别较小,加速度差别较大,并且加速度的差别与水深和风浪大小有一定关系.
加速度是描述风机结构振动的重要指标,振动过大会对风机正常运行造成严重影响.基于本研究结果,对于固定式海上风机,建议在水深和风浪较大的情况下分析风机塔架的动力响应时应考虑流固耦合问题,且同时考虑自由波面的影响,从而减小计算结果的误差.这对风机的设计及工作性能评估均具有现实意义.
[1] MORISON J, JOHNSON J, SCHAAF S. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950,2(5): 149-154.
[2] SARPKAYA T, ISAACSON M. Mechanics of wave forces on offshore structures[M]. New York: Van Nostrand Reinhold Company,1981:25-32.
[3] FISH P, DEAN R, HEAF N. Fluid-structure interaction in Morison's equation for the design of offshore structures[J]. Engineering Structures, 1980,2(1):15-26.
[4] 王元战, 龙俞辰, 王朝阳. 考虑流固耦合影响的桩基波浪力简化计算方法[J]. 水道港口, 2014,35(2):93-98.
WANG Yuan-zhan, LONG Yu-chen, WANG Zhao-yang. Simplified calculation method for wave force of piles under effect of fluid-structure interaction[J]. Journal of Waterway and Harbor, 2014,35(2):93-98.(In Chinese)
[5] 徐亚洲, 李杰. 结构流固耦合波浪动力响应的一阶预估校正法[J]. 船舶力学, 2012,16(7):781-786.
XU Ya-zhou, LI Jie. First order prediction correction method for dynamic wave responses considering fluid-structure-interaction[J]. Journal of Ship Mechanics, 2012,16(7):781-786. (In Chinese)
[6] CHANDRASEKARAN S, JAIN A. Triangular configuration tension leg platform behaviour under random sea wave loads[J]. Ocean Engineering, 2002,29(15):1895-1928.
[7] DNV-OS-J101 Design of offshore wind turbine structures[S]. Oslo,Norway:Det Norske Veritas,2010:48-50.
[8] SHIRZADEH R, DEVRIENDT C, BIDAKHVIDI MA,etal. Experimental and computational damping estimation of an offshore wind turbine on a monopile foundation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013,120:96-106.
[9] AGARWAL P, MANUEL L. Incorporating irregular nonlinear waves in coupled simulation and reliability studies of offshore wind turbines[J]. Applied Ocean Research, 2011,33(3):215-227.
[10]李德源, 刘胜祥, 张湘伟. 海上风力机塔架在风波联合作用下的动力响应数值分析[J]. 机械工程学报, 2009,45(12):46-52.
LI De-yuan, LIU Sheng-xiang, ZHANG Xiang-wei. Dynamical response numerical analysis of the offshore wind turbine tower under combined action of wind and wave[J]. Journal of Mechanical Engineering, 2009,45(12):46-52. (In Chinese)
[11]张学志, 黄维平, 李华军. 考虑流固耦合时的海洋平台结构非线性动力分析[J]. 中国海洋大学学报 :自然科学版, 2005,35(5):823-826.
ZHANG Xue-zhi, HUANG Wei-ping, LI Hua-jun. Nonlinear dynamic analysis of offshore platform considering fluid-structure interaction[J]. Periodical of Ocean University of China, 2005,35(5):823-826. (In Chinese)
[12]GL2010 Guideline for the certification of offshore wind turbines[S]. Uetersen,Germany: Germanischer Lloyd Wind Energie GmbH,2010: 51-58.
[13]徐亚洲, 李杰. 近海风力发电高塔波浪随机动力响应分析[J]. 振动工程学报, 2011,24(3):315-322.
XU Ya-zhou, LI Jie. Dynamic responses of offshore wind turbines subjected to random waves[J]. Journal of Vibration Engineering, 2011,24(3):315-322. (In Chinese)
[14]PIERSON W, MOSKOWITZ L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii[J]. Journal of Geophysical Research, 1964,69(24):5181-5190.
[15]余聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版, 2003:132-136.
YU Yu-xiu. Random wave and its applications to engineering[M]. Dalian:Dalian University of Technology Press, 2003:132-136. (In Chinese)
[16]IEC 61400-1 Wind turbines-Part 1: Design requirements[S]. Geneva,Switzerland: International Electrotechnical Commission, 2005:70-71.
[17]PETERS D, HE C. Correlation of measured induced velocities with a finite-state wake model[J]. Journal of the American Helicopter Society, 1991,36(3):59-70.
[18]LEISHMAN J, BEDDOES T. A semi-empirical model for dynamic stall[J]. Journal of the American Helicopter Society, 1989,34(3):3-17.
[19]JONKMAN J, BUTTERFIELD S, MUSIAL W,etal. Definition of a 5-MW reference wind turbine for offshore system development[R]. Colorado,US:National Renewable Energy Laboratory,2009:2-16.
[20]CHAKRABARTI S K. Hydrodynamic of offshore structures[M]. Berlin: Springer, 1987:45-50.
Numerical Simulation of Dynamic Response for Offshore Wind Turbines including Fluid-Structure Interaction
DENG Lu1†, XIAO Zhi-ying1, HUANG Ming-xi1, SONG Xiao-ping2, WU Hai-tao2
(1.College of Civil Engineering, Hunan Univ, Changsha, Hunan 410082, China;2.XEMC Windpower Co Ltd, Xiangtan,Hunan 411102, China)
This paper investigated the issue of fluid-structure interaction (FSI) for fixed offshore wind turbines. The model for a 5 MW monopile wind turbine built by the National Renewable Energy Laboratory (NREL) was selected as an example. The stochastic inflow turbulence code written by NREL-TurbSim, the Kaimal spectrum and exponential wind profile were used to generate stochastic and full field turbulent wind. The aeroelastic code FAST developed by NREL was then used to calculate the aerodynamic load on the wind turbine. The time histories of shear force and bending moment at the top of the tower were obtained. The random wave was simulated using the Pierson-Moskowits spectrum through the harmony superposition method. Two cases were considered in this study, namely, the case that considered the effect of FSI and the case in which the effect of FSI was neglected. Kinematic equations and numerical models under the two cases were developed respectively, and the comparison between the two cases was made to investigate the effect of FSI. The results indicate that distinct deviations affected by the intensity of the wind and wave exists in both wave force and dynamic responses in the two situations.
offshore wind turbine; random wind and wave; Fluid-Structure interaction; Morison equation
1674-2974(2015)07-0001-08
2014-10-12
国家863计划资助项目(2013AA050603);湖湘青年创新创业平台
邓 露(1984-),男,湖南娄底人,湖南大学教授,博士
†通讯联系人,E-mail:denglu@hnu.edu.cn
TV139.2
A

