城市交通状态的空间依赖性和异质性分析
邹海翔,乐 阳,李清泉
(1.深圳市规划国土发展研究中心,广东深圳518040;2.深圳大学,广东深圳518060)
0 引言
交通数据分析可以为交通规划和决策提供有用信息,因此一直是交通领域的研究热点。交通领域中传统的分析方法是将交通数据看作时间序列数据,以研究单一路段交通数据的时序特征和模式为主要研究目的[1]。这种方法在高速公路、城市快速路等相对封闭道路的研究中取得较好成果。但是交通流在城市路网中具有较大自由度,道路之间存在相互影响。因此城市管理者在决策过程中更为关心路网的整体运行情况,例如交通拥堵发生的地点和扩散范围、交通事故的影响范围等。由于传统方法的研究对象很少涉及路网,因此无法很好地回答道路之间的关联性和交通状态影响范围等反映路网整体运行的问题。
近年来,国内外学者从道路关联性的角度对交通数据分析方法进行研究,主要关注微观和宏观两个层面。微观层面从时间序列的相似性或者先验知识量化多条在拓扑上邻近路段之间的相关程度,并将其作为一种约束条件加入微观交通控制中,以达到数据降维[2]、插补[3]以及提高准确性[4]的目的;这些方法本质上还是基于时序分析的思路,并没有真正描述交通数据的空间特征。而宏观层面主要是基于交通流理论来构建交通仿真模型[5],用数学模型来描述交通系统的运行规律;这类方法计算量大,建模复杂,而且城市交通系统是一个复杂的系统,这些模型很难顾及所有影响因素,因此缺乏可移植性。
随着交通地理信息系统(GIS-T)的发展,有学者提出GIS中的空间分析理论可以直接用于解决交通领域的实际问题[6-8]。从经验出发不难发现,城市交通拥堵现象具有一定的周期性和区域性:通勤时间的拥堵现象比平时更为严重,而且重要路段和交叉口附近是拥堵现象发生的热点区域。这和地理学第一定律[9]中关于地理现象空间相关特征的描述是相符的。因此,可以把城市交通系统看作是一种复杂的空间过程,并且从空间角度来分析城市交通数据,这样就可以从本质上描述交通数据的整体特征,从而反映城市交通系统的整体运行情况。本文的研究目的是从空间分析理论最核心的空间依赖性和空间异质性[10]对城市交通数据进行分析,研究城市交通状态和路网空间形态之间的关系,从宏观上描述交通运行的空间特征。
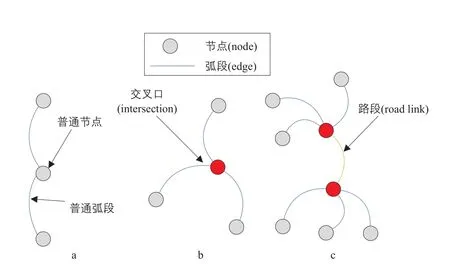
图1 交叉口和路段示意Fig.1 Illustration of intersections and roadway segments
1 基于路网结构的交通数据分析模型
在进行空间分析前首先要对研究对象进行抽象,得到具有均匀属性的空间对象。基于空间分析理论对空间对象的分布特征进行分析时主要关注点状和面状的对象,而交通路网在几何形态上由很多线状的路段组成,故无法直接使用空间分析理论进行分析。因此,本文针对城市路网的空间结构提出一种城市路网的抽象方法,并建立适合于城市交通数据空间分析的模型。
首先给出交叉口和路段的定义。
定义1:路网中的交叉口采用节点-弧段模型中的节点来表示,是由两条以上具有拓扑邻接路段构成的交点。
定义2:路段是两个连续交叉口之间的弧段。
图1展示了三种由节点-弧段模型形成的路网结构,其中,图1a中间的节点由于只有两条邻接路段,因此只是普通节点而不是交叉口,而下方的弧段只和两个普通节点邻接,因此只是普通弧段而不是路段;图1b是标准的交叉口结构,图1c是标准的路段结构。
假设路段交通状态在短时段Δt(例如5 min)内是均匀的,可以将路段按照Δt的粒度抽象为点状空间实体,而Δt内的各种交通数据(例如行程速度、流量等)可作为“点状”路段的属性值。
定义3:在短时段Δt内,城市交通路网是所有路段的中点所构成的空间离散点,每个Δt内的交通数据是一组截面数据,因此长时期内的交通数据可以看作是许多截面数据的集合(见图2)。
距离是空间统计学中衡量空间实体之间相关性的参数,其中自由空间中两点之间的距离一般采用欧式距离。但是在交通路网中,路段之间的可达性受到路网结构的约束,因此描述两条路段之间的距离不能采用欧式距离。由于路段的交通状态在短时间内不受路段长度的影响,并且交叉口的空间位置是固定的,所以本文采用从一条路段到另一条路段经过的交叉口数量表示二者之间的距离。
定义4:两条路段之间的距离是从起始路段到终止路段所经过的最少交叉口数量N,即交叉口距离。
2 实验数据
浮动车因其覆盖广的特点已经成为目前最常用的一种采集大规模路网交通数据的手段。本研究为尽可能多的采集路段交通数据,采用浮动车数据作为实验的原始数据。
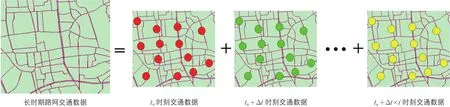
图2 将长时期交通数据按照某个短时段Δt划分为截面数据的集合Fig.2 Long-term traffic data divided into several cross-section data at certain short time intervalΔt
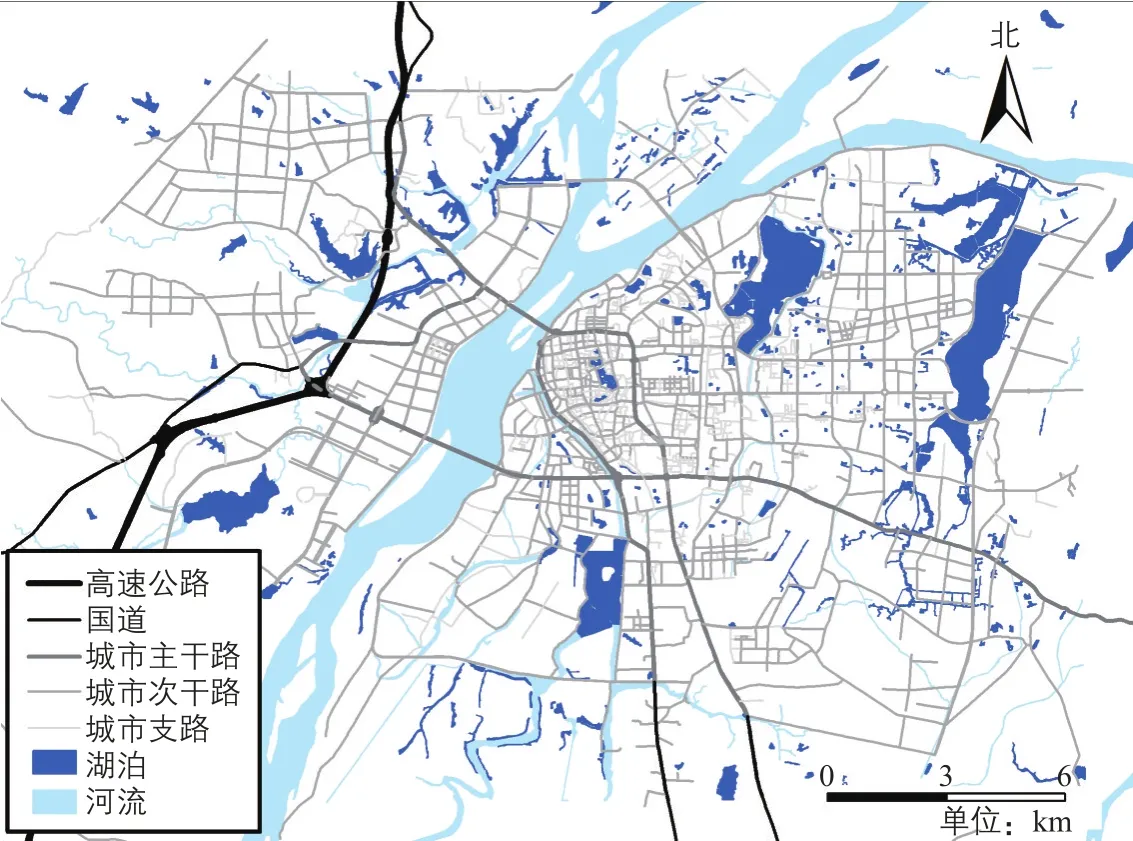
图3 南昌市区路网结构Fig.3 Roadway network structure in Nanchang City
2.1 城市路网行程速度数据
为保证分析的准确度,需要采用长期且大量的原始数据,而且要满足覆盖率的要求[11]。选取南昌市浮动车系统采集的浮动车数据作为原始数据,采集时间为2008年7月14—20日和2009年1月1—14日,共计3个星期,其中包括7个节假日。南昌市浮动车系统采用的频率按照每隔100 m和400 m两种模式发送信号,平均发送时间间隔为40 s,覆盖市区90%以上的路段。
行程速度作为一种典型的交通数据,可以反映道路的交通运行状态[12]。以往的研究曾提出基于车辆轨迹的路段行程速度提取方法[13],这种方法可以从浮动车数据中提取出路段在固定时段内的行程速度值,因此本研究采用交通领域常用的反映路段实时运行状态的5 min作为时间粒度,以5 min的路段平均行程速度作为交通数据样本。另外,由于0:00—6:00的浮动车覆盖率很低,且该时段车流量极少,对城市整体交通而言研究价值不大,因此剔除该时段的数据。这样,一条路段一日中理论上可以采集到216个样本
2.2 城市路网数据
本文选择南昌市区路网作为实验的路网数据,其中包括4 359条路段,按照道路功能可以分为高速公路、主干路、次干路和支路(见图3)。其中,部分路段由于覆盖率的问题导致行程速度值缺失严重,影响分析精度,因此在实验过程中剔除行程速度缺失率高于25%的路段。
2.3 城市交通的典型时段划分
以日为单位的交通数据在时序上存在多种模式,相同模式的交通数据具有相似性,而不同模式的交通数据具有显著的差异性,为分析城市交通在不同模式的空间特征,有必要对其进行时段划分。
首先计算2008年7月14日(星期一)至20日(星期日)所有路段5 min行程速度的平均值,以此作为路网5 min的整体速度,然后对7:00—23:00的路网整体速度两两计算Pearson相关系数(见图4)。
实验结果显示,工作日和非工作日(节假日)的路网整体交通状态具有显著差异,但是工作日之间和非工作日之间又存在相似性。另外,实验选择每日8:00—9:00作为早高峰时段,15:00—16:00作为平峰时段,18:00—19:00作为晚高峰时段,对路段每日不同时段的速度分布情况进行分析(见图5)。工作日具有明显的“三峰”特征,而非工作日不明显。因此,将城市路网行程速度划分为工作日早高峰、平峰、晚高峰和非工作日4个典型时段。
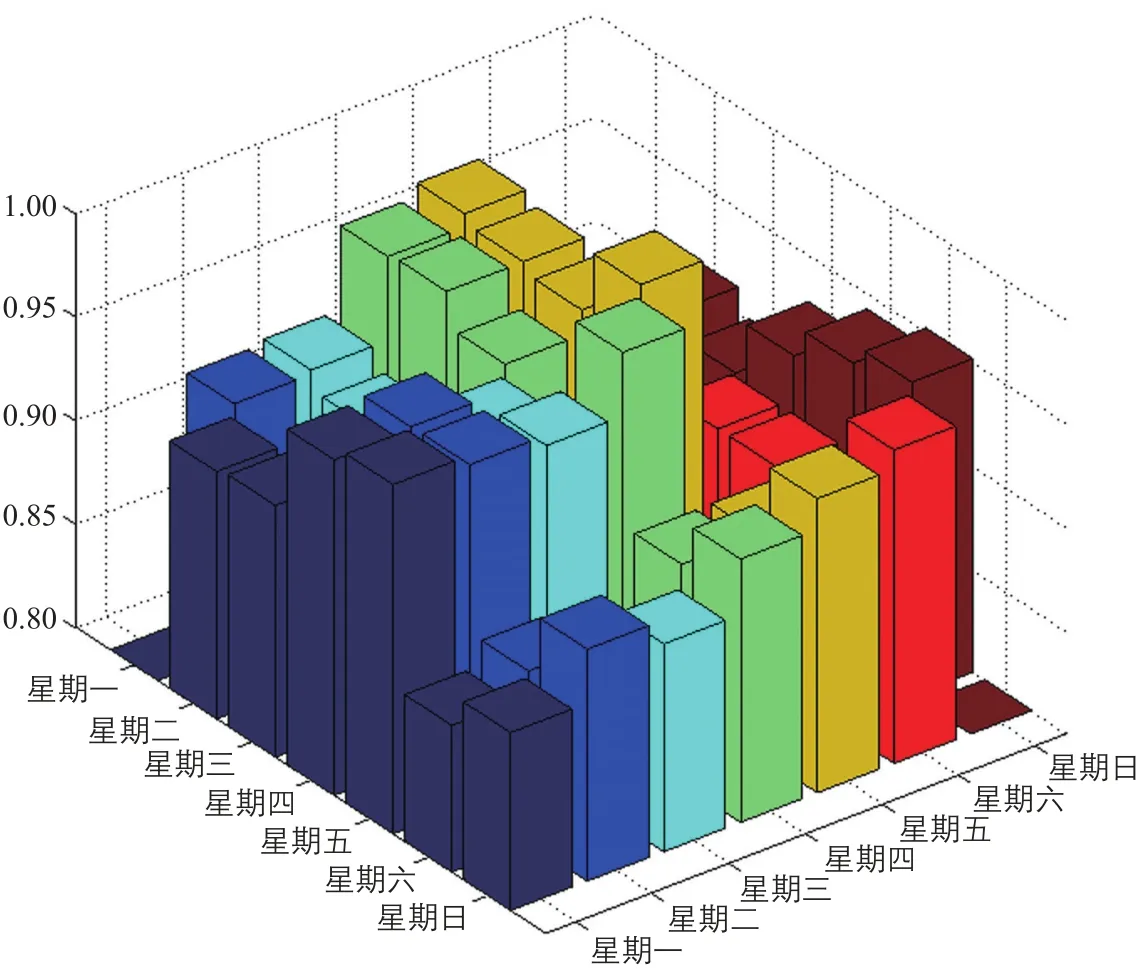
图4 路网行程速度的Pearson相关系数比较Fig.4 Comparison of Pearson correlation coefficients of travel speeds on roadway networks
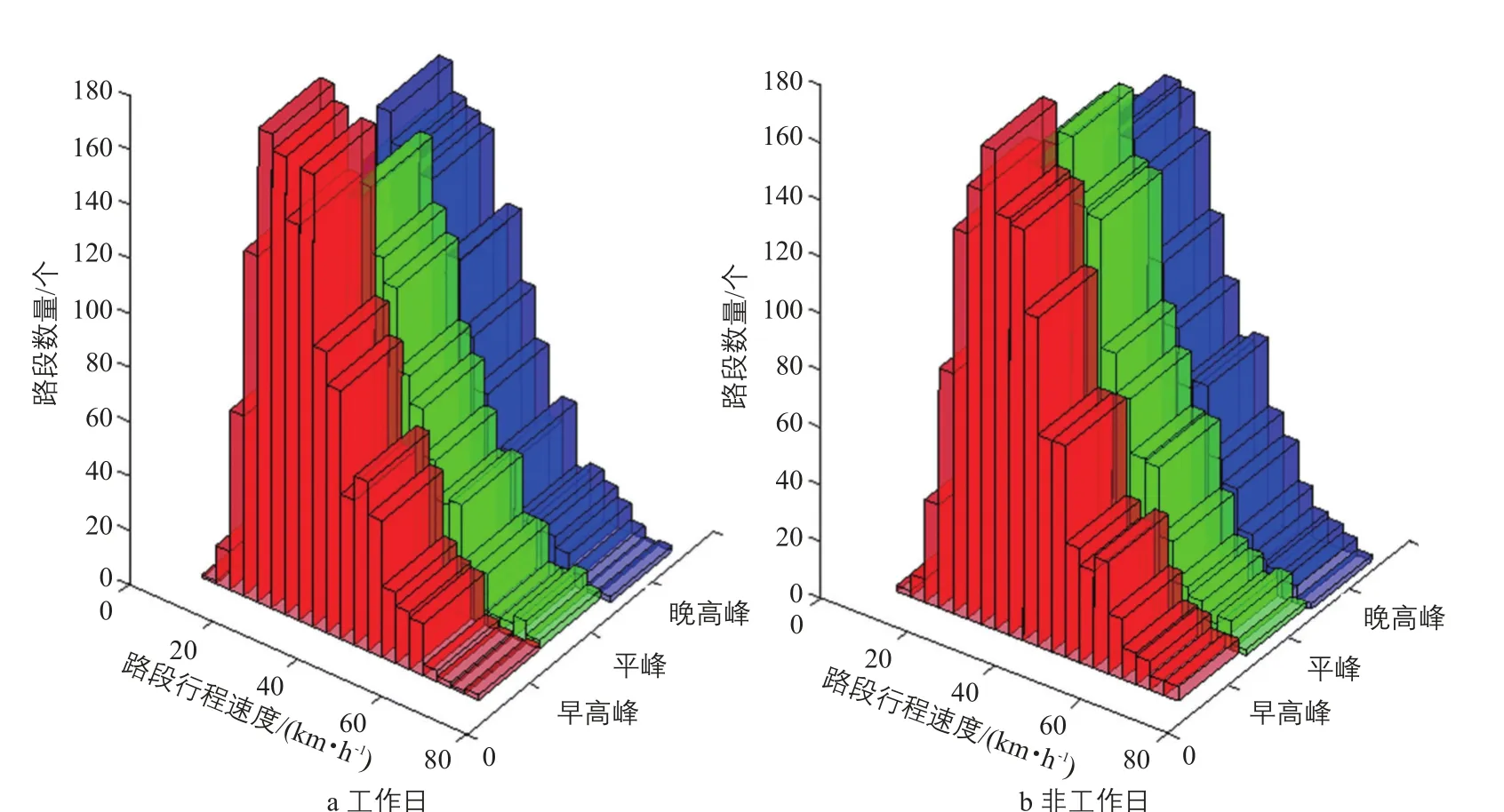
图5 路段行程速度分布Fig.5 Distribution of travel speeds on roadway segments
3 城市路网行程速度的空间分析
3.1 空间依赖性
在空间分析理论中,空间依赖性用来反映空间对象某种属性的空间模式[10]。空间自相关分析(Spatial Autocorrelation Analysis)是度量空间依赖性的手段,常用的方式是通过全局或局部空间统计来量化空间自相关,从而反映空间对象的空间依赖程度。其中,全局统计量用来判断空间对象整体的空间自相关程度,而局部统计量反映空间对象在空间中的集聚程度。
通过分析整体路网的空间依赖性可以发现城市交通运行中路段之间的空间关联程度,这有利于描述路段交通状态对整体路网交通状态的空间影响力。本文采用经典的全局Moran I统计量作为指标。全局Moran I的定义如下[14]:
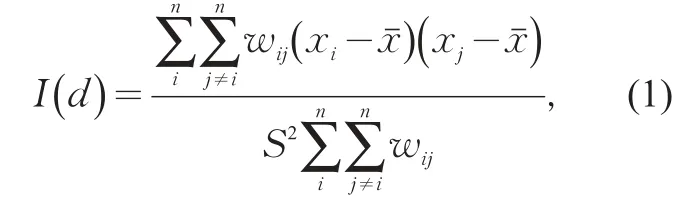
式中:wij是空间权重矩阵(Spatial Weight Matrix,SWM),以数值来量化空间实体之间的邻近程度,根据不同的应用有许多不同的空间权重矩阵定义方法,其中比较常用的是二进制SWM和基于距离的SWM;xi和xj分别为属性X(此处指路段速度)位置i和位置j上的观测值;S2为属性X的方差;是{xi}的均值。Moran I值通常为-1~1,正值表示属性具有正空间自相关性,负值表示负空间自相关性,其绝对值越大表示空间自相关程度越强。
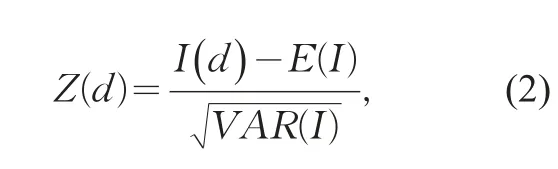
另外,一些学者提出Z-score统计量对Moran I进行显著性检验,在零假设为Moran I服从正态分布的情况下,Z-score的形式为[9]式中:E(I)为Moran I的期望;VAR(I)为Moran I的方差。当|Z|>1.96时拒绝零假设,表示空间对象之间存在空间自相关性,否则不存在。
本实验为计算城市交通数据的全局Moran I,以路段行程速度作为属性X。首先采用Anselin提出的方法[15]构建高阶SWM:
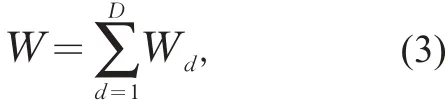
式中:d为阶数,D为阶数上限,Wd为阶数取值为d时的SWM值。按照定义4分别构建7个不同阶数的SWM,其中阶数也可以称为连接层次,表示两路段邻近的标准,越低阶的SWM表示邻近标准越苛刻,其邻近路段也越少;其在空间上表现为从某路段出发,按照拓扑层次关系搜索到的所有路段的集合。图6和表1分别显示在典型时段交通数据全局Moran I和其Z-score的计算结果。
由表1可见,4个时段内的Z-score都远远大于1.96,表明城市交通数据存在显著的空间自相关性。但是图6显示,Moran I值随着阶数的增长不断衰减,并且从5阶开始趋向于0(<0.1),说明路段之间的相关性随着距离的增长不断减弱,并且增长至一定距离之后将会逐渐消失(例如本文的实验结果为5阶,说明单一路段的影响范围一般不超过5个交叉口)。上述分析结果与先验知识相符合:邻近路段的交通状态存在相似性,但是当超过一定范围之后路段间交通状态的差异也会随之增大。通过分析可以量化城市路网交通状态的相关程度,这对于交通事件影响范围和变化规律的研究具有重要意义。
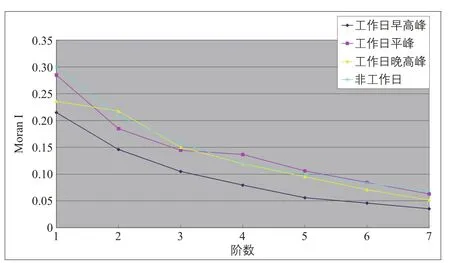
图6 城市路网行程速度在典型时段的全局Moran IFig.6 Network-wide Moran I for travel speeds at typical time intervals
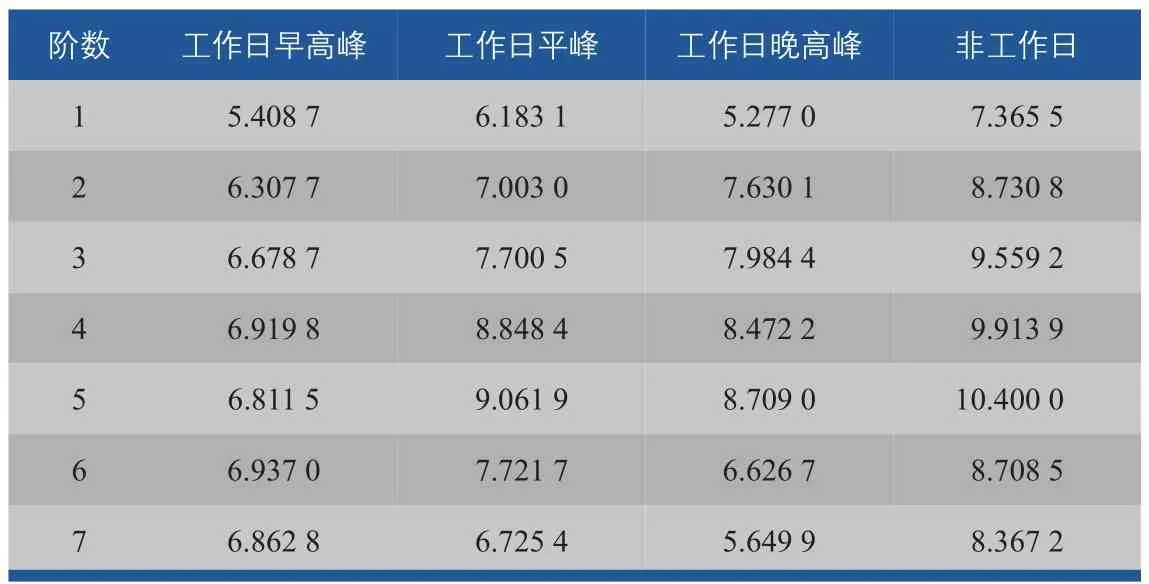
表1 城市路网行程速度全局Moran I的Z-score检验结果Tab.1 Z-score test results of network-wide Moran I for travel speeds
3.2 空间异质性
空间异质性在空间分析理论中用以反映空间对象分布的不稳定程度。对空间对象来说,空间异质性和空间依赖性同时存在,表现为存在整体上的关联性和不均匀的局部集聚现象[6]。
通过对城市交通空间异质性的分析可以从宏观上发现城市交通状态在空间中的影响程度和范围,结合交通状态的时变特征还可以用于描述城市交通在一定时期内的演变规律。本实验引入核密度估计(Kernel Density Estimation,KDE)方法分析城市交通的异质性,这是一种在空间分析领域常用的趋势面分析(Trend Surface Analysis)方法,其优点是能够用连续函数来描述空间对象的分布特征,具有较好的可视化效果,比较适合宏观分析。KDE方法的核心公式如下[16]:
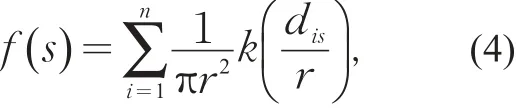
式中:f(s)为位置s处的密度值;r为搜索半径(带宽),只有在r范围内的空间对象才能用于计算f(s);k为到s距离为dis的点i的权重值,通常用自变量为dis和r比值的函数来表示(核函数)。目前常用的核函数包括Gaussian,Quartic和Minimum Variance方程,但是以往的研究发现带宽的选择比核函数的选择更重要[16]。为尽可能细化分析结果,本实验选择500 m带宽(在市中心区500 m范围内至少会出现5条路段,可以充分保证分析的精度)。
图7显示基于KDE方法构建的工作日早高峰行程速度的密度趋势面,不同颜色表示不同密度,其中越趋向于红色表示行程速度越低,越趋向于绿色表示行程速度越高。结果显示:1)行程速度在空间中的密度分布具有明显的不均匀性,这说明行程速度的分布存在局部集聚现象;2)从密度值的空间分布可以判断不同交通状态的空间分布情况,有利于从宏观上直观地发现各种交通状态的影响范围。更进一步,对南昌市商业区较集中的区域A和居民区较集中的区域B的行程速度分布情况进行比较发现,同一时段内交通状态的空间分布受到区域功能的影响:商业区A在早高峰时段路段行程速度在20~30 km·h-1分布比较集中,而居民区B在30~40 km·h-1分布比较集中,这说明商业区在早高峰时段的交通状况比居民区差,这主要受城市居民出行的影响,但同时也与商业区密集的路网结构有关(见图8)。
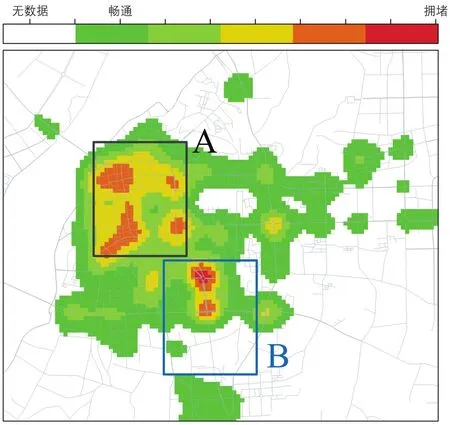
图7 南昌市工作日早高峰时段行程速度分布Fig.7 Distribution of travel speeds during weekday morning peak hours in Nanchang City
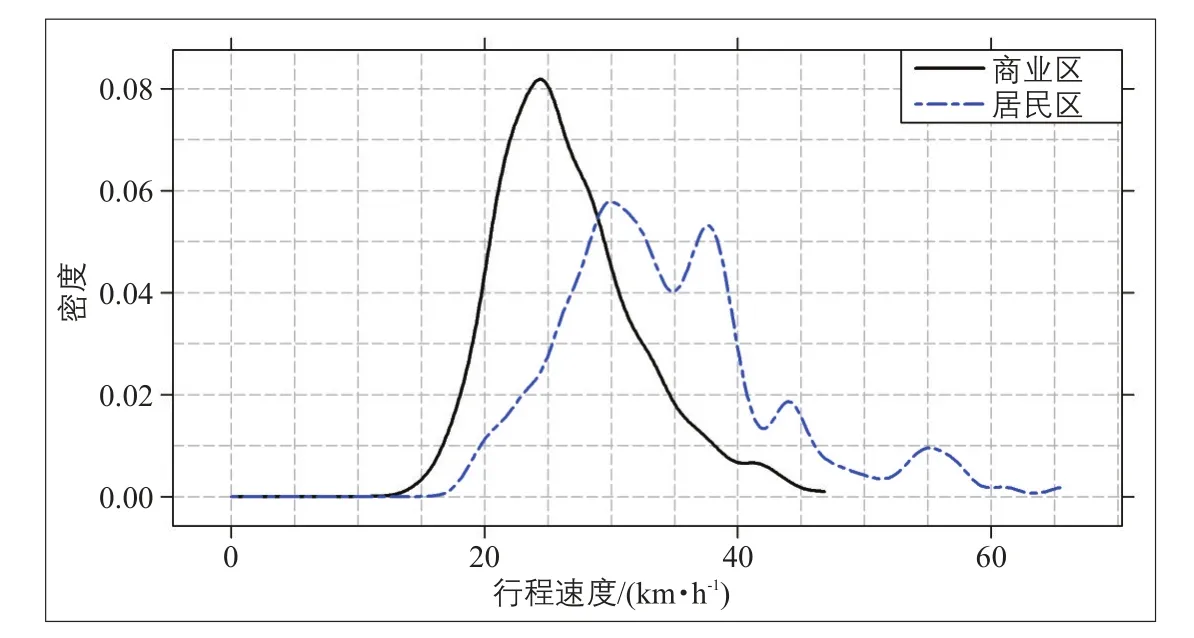
图8 商业区和居民区工作日早高峰时段行程速度分布Fig.8 Distribution of travel speeds during weekday morning peak hours in commercial and residential areas
3.3 空间分布特征
基于路段位置和路网空间形态,详细分析路网行程速度的空间分布特征,并通过量化的结果对交通运行中的空间模式进行分析。首先,选取城市路网的几何中心作为空间基准:根据定义3获得所有路段位置的经纬度,并用其平均值作为城市路网的几何中心位置然后,将每个时段与中心位置的距离和行程速度视为一组样本,其中D是按照定义4计算出的路段距中心位置的距离(单位为交叉口数量),V表示路段的行程速度。
如图9所示:1)所有时段90%以上的样本都集中在一个扇面区域内,说明路段行程速度和位置之间不存在线性关系,呈现空间上的不稳定性;2)扇面区域的张角在不同时段具有不同特征,说明交通数据的空间分布随时间变化,呈现时间上的不稳定性,其中工作日早高峰时段的夹角最小,这反映工作日早高峰时段路网行程速度的空间分布较其他时段更为均匀。城市交通数据受到路段空间位置的影响而存在差异,因此本文的研究过程在路网形态相异的城市可能会得到不同的结果。
上述实验粗略分析了交通数据和路段几何位置的关系,为得到更加精细的结果,将每个时段所有路段行程速度的样本按照从小到大的顺序排列并三等分,分别按值的大小命名为低速样本、中速样本和高速样本,样本分布情况如图10所示。
忽略不同时段空间分布特征的局部差异,可以从整体上得到如下结论:1)低速样本主要分布在离中心位置较近的区域;2)中速样本比高速样本在距中心位置较近的区域分布得更多,但是在距中心位置较远的区域两者的分布相近;3)所有样本的分布曲线都具有多个波峰和波谷,利用这些波峰和波谷可以发现城市交通中的热点和冷点区域。例如,工作日早高峰时段低速样本分布频数最高值约为15,说明距离城市中心15个交叉口附近的路段交通状态最差;同样,从高速样本曲线可以发现工作日早高峰时段距离市中心25,35和40个交叉口附近的路段交通运行比较理想。
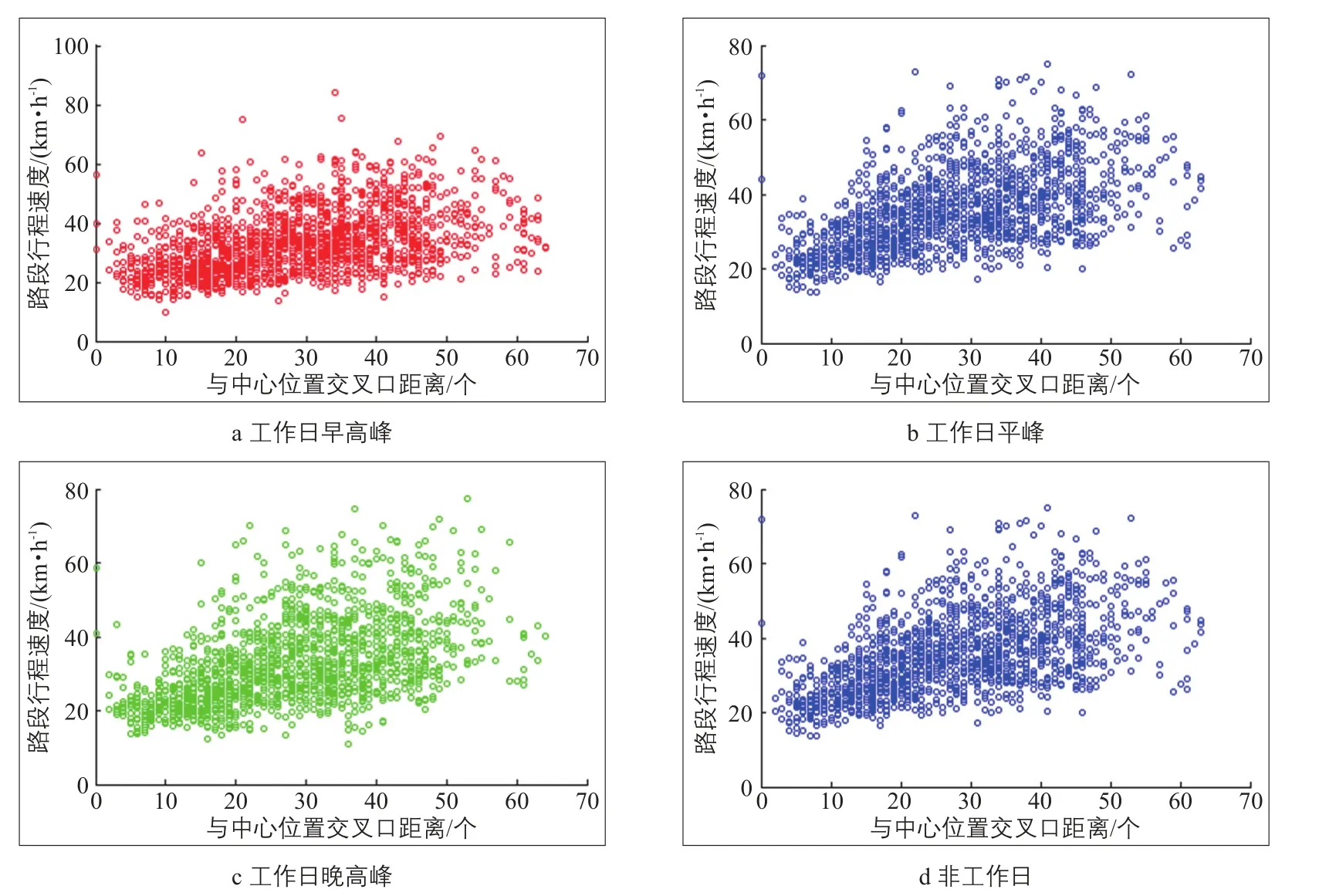
图9 典型时段路段到中心位置的距离与行程速度的关系Fig.9 Relationship between the distance from road segments to the central location and travel speeds at typical time intervals
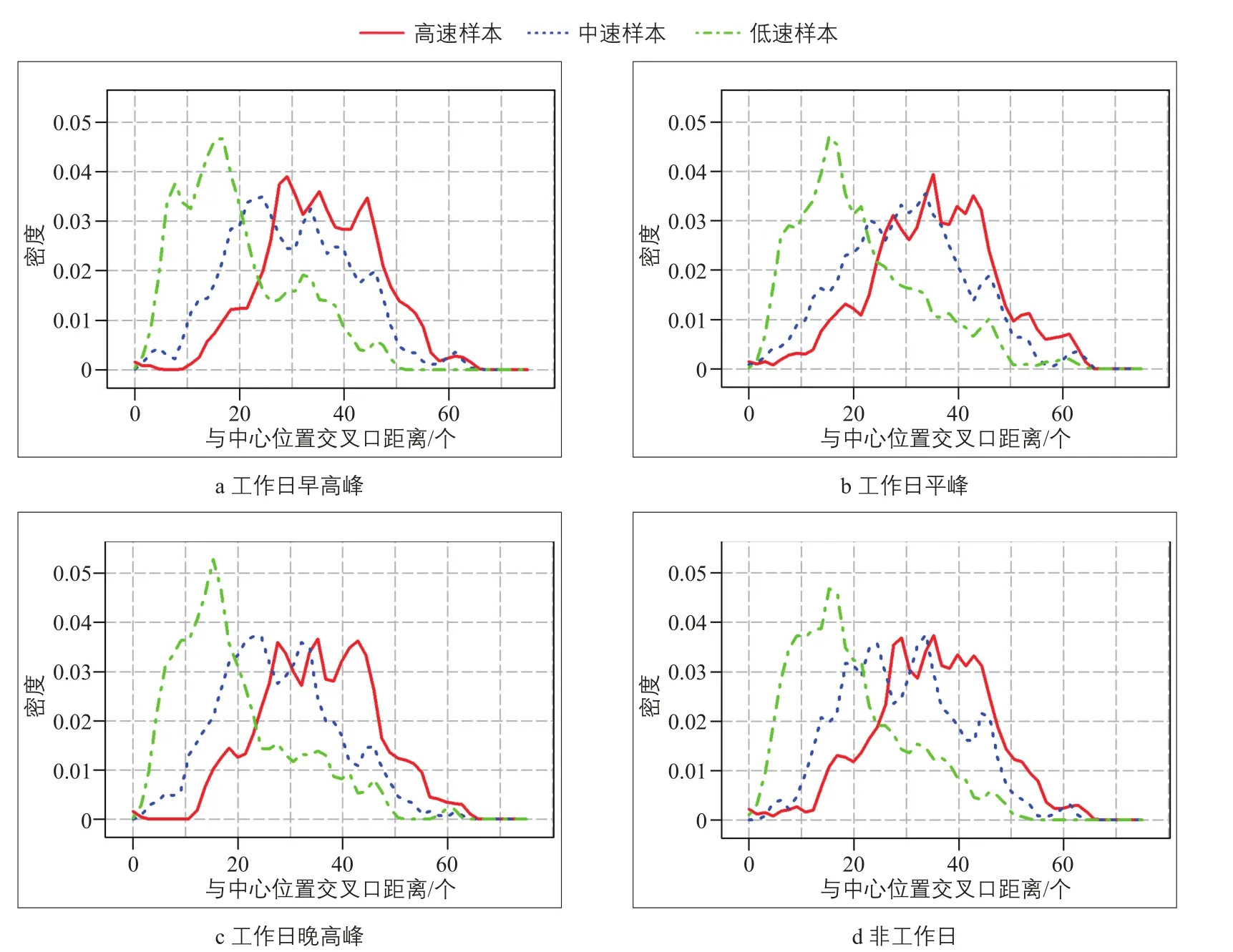
图10 典型时段不同速度等级路段到中心位置的距离分布Fig.10 Distribution of distance from road segments with different travel speeds to central location at typical time intervals
4 结论
本文将城市交通系统视为一种复杂的空间过程,将空间分析方法引入交通数据分析,并且针对城市路网几何结构和交通状态的关系提出适合城市交通数据分析的空间模型,为交通领域研究提供新的思路,同时也为空间分析理论提供新的应用领域。通过对从大量浮动车数据中提取的真实交通数据进行分析,论证城市路网交通数据中存在空间依赖性和空间异质性,这反映出城市交通状态存在局部相似性,同时又在时空上呈现不稳定性。
根据文中的分析结论,一方面可以从宏观上发现城市交通运行的实时空间特征以及长期演变规律,有效地发现城市交通系统的整体运行特点,为城市管理者提供决策支持,为解决城市交通问题提供新途径;另一方面还可以分析路段交通状态的影响力和影响范围,为交通疏导、交通控制等微观层面的应用提供有效的信息支持。本研究证实空间模型在交通系统中应用的可行性,因此将这些具有空间特征的模型具体用于解决各种实际交通问题将是今后的工作重点。
[1]Willinger W,Taqqu M,Erramilli A.Stochastic Networks:Theory and Applications[M].Oxford:Oxford Science Publications,1996:339-340.
[2]宫晓燕,陈伟雄.基于关联规则挖掘的路段流量关系的分析[J].公路交通科技,2003,20(4):63-66.Gong Xiaoyan,Chen Weixiong.Study on Relationship among Adjacent Road Segments Traffic Based on Association Rules Mining[J].Journal of Highway and Transportation Research and Development,2003,20(4):63-66.
[3]Kumagai M,Fushiki T,Kimita K,Yokota T.Spatial Interpolation of Real-time Floating Car Data Based on Multiple Link Correlation in Feature Space[C/OL]//13th World Congress of ITS,CD-ROM,London,October 8-12,2006.[2015-03-01].http://www.researchgate.net/publication/267410128_SPATIAL_INTERP OLATION_OF_REAL-TIME_FLOATING_CAR_DATA_BASED_ON_MULTIPLE_LINK_CORRELATION_IN_FEATURE_SPACE.
[4]韩卫国,王劲峰,高一鸽,胡建军.区域交通流的时空预测与分析[J].公路交通科技,2007,24(6):92-96.Han Weiguo,Wang Jinfeng,Gao Yige,Hu Jianjun.Forecasting and Analysis of Regional Traffic Flow in Space and Time[J].Journal of Highway and Transportation Research and Development,2007,24(6):92-96.
[5]Salvini P A,Miller E J.ILUTE:an Operational Prototype of a Comprehensive Microsimulation Model of Urban Systems[J].Networks and Spatial Economics.2005,5:217-234
[6]Miller H J.Potential Contributions of Spatial Analysis to Geographic Information Systems for Transportation(GIS-T)[J].Geographical Analysis,1999,31(4):373-399.
[7]Miller H J,Shaw S L.Geographic Information Systems for Transportation:Principles and Applications[M].Oxford: Oxford University Press,2001.
[8]方志祥,李清泉,萧世伦.利用时间地理进行位置相关的时空可达性表达[J].武汉大学学报·信息科学版.2010,35(9):1091-1095.Fang Zhixiang,Li Qingquan,Shaw Shihlung.Representation of Location-Specific Space-Time Accessibility Based on Time Geography Framework[J].Geomaticsand Information Scienceof Wuhan Univers,2010,35(9):1091-1095.
[9]Tobler W R.A Computer Movie Simulating Urban Growth in the Detroit Region[J].Economic Geography,1970,46:234-240.
[10]王劲峰,等.空间分析[M].北京:科学出版社,2006.Wang Jinfeng,etc.Spatial Analysis[M].Beijing:Science Press,2006.
[11]李清泉,尹建忠,贺奋琴.面向道路网的GPS浮动车覆盖率模型研究[J].武汉大学学报·信息科学版.2009,34(6):715-718.Li Qingquan,Yin Jianzhong,He Fenqin.A Coverage Rate Model of Gps Floating Car for Road Networks[J].Geomatics and Information Science of Wuhan Univers,2009,34(6):715-718.
[12]姜桂艳.道路交通状态判别技术与应用[M].人民交通出版社,2004:49-52.
[13]Yue Yang,Zou Haixiang,Li Qingquan.Urban Road Travel Speed Estimation Based on Low Sampling Floating Car Data[C]//Wang Yinhai,Yi Ping,An Shi,Wang Hua.Critical Issues in Transportation System Planning,Development,and Management.Harbin:American Society of Civil Engineers,2009:1719-1725.
[14]Cliff A D,Ord J K.Spatial Process:Models andApplications[M].London:Pion,1981.
[15]Anselin L,Smirnov O.Efficient Algorithms for Constructing Proper Higher Order Spatial Lag Operators[J].Journal of Regional Science,1996,36(1):67-89.
[16]Xie Z,Yan J.Kernel Density Estimation of Traffic Accidents in a Network Space[J].Computers,Environment and Urban Systems,2008,32(5):396-406.

