基于MIDAS/GTS的尾矿库三维渗流分析

王少军 丁东彦

(兰州有色冶金设计研究院有限公司)

基于MIDAS/GTS的尾矿库三维渗流分析

王少军 丁东彦

(兰州有色冶金设计研究院有限公司)

为了较为真实地模拟实际地形条件对尾矿坝渗流场的影响，采用MIDAS/GTS软件自带的地形生成器导入实际地形，建立了二维、三维有限元模型，对实际工程渗流场进行了数值模拟，并计算出了浸润线的位置。结果表明，由于地形条件的限制，导致简化的二维模型的计算结果与实际监测值相差较大，而三维模型的计算结果与实际监测值基本吻合。

MIDAS/GTS 渗流分析 有限元模型

尾矿库是一种具有高势能的人造泥石流危险源，随着矿山工业的发展，我国尾矿库的数量越来越多，坝体的堆积也越来越高，随之而来的是危库、险库、病库也逐渐增加。通过对已有的尾矿库事故进行调查分析可知，大多数溃坝事故与坝体浸润线过高密切相关。尾矿库大多依山而建，地形比较复杂，导致尾矿库的渗流是一个比较复杂的三维空间问题，但目前工程设计中均将其简化为平面问题进行二维分析处理。由于复杂多变的地形条件对尾矿库渗流场的影响很大，导致简化的二维数值模型无法有效模拟尾矿库的真实渗流场，因此，为了更真实地反映尾矿库的渗流特性，采用大型有限元软件MIDAS/GTS对尾矿库进行三维渗流数值分析。

1 尾矿库三维渗流有限元分析方法

1.1 基本方程

(1)

式中，H为水头函数；kx、ky、kz分别为x、y、z方向的渗透系数。

1.2 边界条件

根据渗流区域几何边界上的水力性质，边界条件可分为水头边界条件和流量边界条件2种[2]，分别定义如下

(2)

式中，H(x,y,z)为待求解的水头函数；f(x,y,z)为边界Γ1上的已知水头函数；Γ1、Γ2分别为已知水头值和流量值的边界曲面；q为边界Γ2上的已知单位流量，L/s；n为边界Γ2的外法线方向。

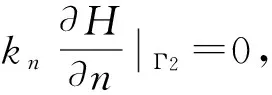
1.3 有限元分析方法

将式(1)、式(2)转变为一个泛函I(H)求极值的问题，根据变分原理，在稳定渗流区域Ω中构造的泛函为

虽然两者存在一定的区别，但在容错纠错机制的讨论中，笔者倾向于将两者进行结合讨论，原因在于容错纠错机制对程度较为严重的错误都进行容忍，那么对于更轻者瑕疵理应持更加宽容的态度。进而言之，瑕疵本意为玉的斑痕，引申为不足和过失。工作中的瑕疵当然属于可以原谅和容忍的范畴，属于容错的范畴。

(3)

将三维空间渗流场采用四面体单元进行剖分，剖分后每个单元有4个节点[3-4]。假定水头函数在四面体单元4个顶点上的值在四面体单元内近似按线性函数分布，且单元内渗透系数为常数。得到剖分后每个单元的泛函及导数，对渗流场所有单元的泛函进行微分后再进行叠加。为了满足整个渗流场I(H)为极小的条件[5]，则有

(4)

式中，m′为以i为公共节点的单元数。

n个未知水头节点的线性代数方程为

F=KH，

(5)

式中，F为由已知水头节点的水头形成的常数列向量；K为总渗透矩阵；H为未知水头节点的水头列向量。

采用有限元法求解渗流场的问题可转换为求解关于未知水头的线性方程组，结合边界条件求解式(5)便可直接得到以结点水头值表示的近似稳定渗流场。

2 工程实例

2.1 工程概况

某尾矿库为山谷型尾矿库，采用水力充填法上游式尾砂筑坝，库内设排渗井设施，初期坝高为8.0 m，高程为568.2～570.0 m，初期坝为当地材料不透水坝。尾矿堆积坝坝顶高程为626～626.5 m，尾矿坝高为67 m，坝顶长153.3 m，坝顶至库内3#排水井的距离约200 m，其中水面长约100 m，干滩长为180 m，左岸有简易路可通至600 m高程，坝体位于589.0 m高程处，尾砂坝体向上游方向水平推进45 m，形成水平大平台，平台下部不规则坝体平均坡度为1∶4.2，平台上部尾矿不规则坝体平均坡度为1∶3.0，大平台上部坝高35 m。

2.2 三维有限元分析

2.2.1 模型建立及参数选取

采用MIDAS/GTS软件自带的地形生成器生成实际地形导入，模型坐标原点位于初期坝下游坡脚最低点处，选取自下游向上游方向为Z轴正方向，自下向上为Y轴方向，自左向右为X轴方向，模型材料参数见表1。

表1 模型材料参数

单元尺寸设为10 m，自动映射划分网格，二维模型共划分单元数1 130个，节点数1 229个，三维模型共划分单元数14 244个，节点数7 907个，见图1。

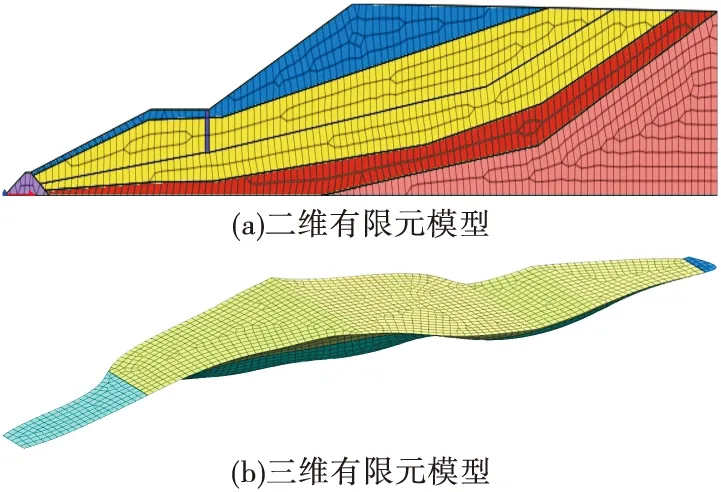
图1 尾矿坝二维、三维有限元模型

2.2.2 计算结果

通过计算得到该尾矿库正常工况下设计水位为222 m时的浸润(线)面分布情况见图2。由图2(a)可知浸润线位置整体较低，在初期坝上游水跌现象不太明显；由图2(b)可知浸润线整体位置比较高，在初期坝上游出现了明显的水跌现象。

该尾矿库二维数值模拟结果、三维数值模拟结果与实际监测结果对比见图3。由图3可知，由于二维数值模型无法充分反映尾矿库复杂多变的地形特征，使得计算结果与实测值相差较大，二维计算所得的浸润线低于三维和实测结果，则偏于危险；而三

图2 二维、三维浸润线云图

维计算结果与实测值相吻合，且浸润线位置高于二维和实测值，偏于安全。因此，简化的二维渗流计算结果存在严重缺陷，对后期尾矿库的设计不利。

3 结 语

将MIDAS/GTS软件运用到尾矿库的三维渗流分析中，通过模拟实际地形条件对尾矿库渗流场的影响，建立了二维、三维有限元模型，并计算确定出了浸润线的位置。通过对计算结

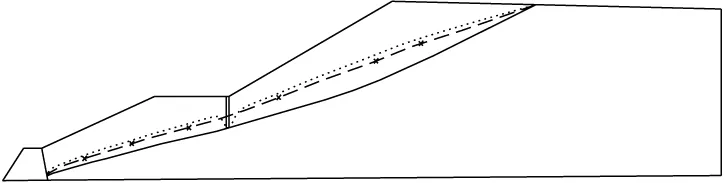
图3 二维、三维计算结果对比

果与实际监测值进行对比分析可知，相对于二维简化模型，三维模型计算结果较为准确，与实际监测值基本吻合，有利于为尾矿库的后续设计。

[1] 杜延龄，许国安.渗流分析的有限元和电网络法[M].北京：水利电力出版社，1992.

[2] 魏泽光，黄 俊，许国安，等.三维稳定渗流的有限元计算[J].水利学报，1982(1)：39-47.

[3] 田莉梅.尾矿库坝体渗流特征分析及其稳定性研究[D].北京：北京科技大学，2009.

[4] 柳厚祥，宋 军，陈克军.尾矿坝二维固结稳定渗流分析[J].矿冶工程，2002，12(22)：8-14.

[5] 赵 坚，纪 伟.尾矿坝地质剖面概化及其对渗流场计算的影响[J].金属矿山，2003(12)：29-31.

2015-01-22)

王少军(1965—)，男，高级工程师,730000 甘肃省兰州市天水南路168号。