基于人工神经网络的中深孔爆破参数优选
谢经鹏 明世祥 梁新民
(北京科技大学土木与环境工程学院)
基于人工神经网络的中深孔爆破参数优选
谢经鹏 明世祥 梁新民
(北京科技大学土木与环境工程学院)
为了得到合理的中深孔爆破参数,以矿岩的弹性模量、容重、抗拉强度、抗压强度、摩擦角以及黏结力作为输入因子,以炮孔的崩矿步距、孔底距以及炸药单耗为输出因子,以国内爆破工艺相类似矿山的相关数据为训练样本,建立BP神经网络模型进行爆破参数优选。以港里铁矿为工程背景,通过优选和影响因素分析,得到崩矿步距1.67 m,孔底距1.8 m,炸药单耗0.43 kg/t的爆破参数。使用后证明,比原炸药单耗(0.52 kg/t)降低了17.3%。
中深孔爆破 BP神经网络 参数优选
港里铁矿以无底柱分段崩落法开采,以扇形中深孔挤压爆破崩矿矿岩,在生产过程中存在炸药单耗大、大块率高的问题。孔底距、崩矿步距以及炸药单耗是最主要的爆破参数[1],分析影响爆破参数的主要因素,包括容重、弹性模量、抗拉强度、抗压强度、摩擦角及黏结力。爆破参数与影响因素之间关系比较复杂,很难确定其相关性,因而合理爆破参数的选择是一个多层次、多因素、多目标的复杂过程[2]。
在生产实践中,国内矿山大都采用工程类比法和现场爆破实验来确定爆破参数,前者因地质条件等因素的影响,具有很大的不确定性;后者既耗时又耗力,难以达到理想的效果[3]。
本文使用BP人工神经网络建立爆破参数与主要影响因素间的非线性模型,通过查阅相关文献资料,选取国内相似的爆破数据作为网络的训练样本,然后对爆破参数优选。通过BP神经网络的优选,可以克服耗时、耗力等缺点,具有很大的便捷性。
1 人工神经网络模型的建立
1.1 BP神经网络原理
BP神经网络是一种单向传播的多层前向神经网络,简称BP算法,是利用输出后的误差来估计输出层的直接前导层的误差,再利用这一误差估计更前一层的误差,如此一层一层的反传下去,获得了所有各层的误差估计[4]。通过这种方式,程序逐层把输出层显现的误差传到与输入传送相反方向的输入层。
典型的BP神经网络包括三层网络结构,即输入层、隐含层和输出层。如图1 所示。

图1 BP神经网络结构
在网络结构中,输入层的向量用X=(x1,x2,…,xn)T表示;隐含层的输出向量用Y=(y1,y2,…,ym)T表示;输出层向量用O=(o1,…,ok,…,ol)T表示;期望输出向量用d=(d1,d2,…,dk,…,dl)T表示。输入层和隐含层之间用权值矩阵V表示,V=(V1,V2,…,Vj,…,Vm),其中列向量Vj代表隐含层的第j个神经元对应的权向量;隐含层到输出层之间用权值矩阵W表示,W=(W1,W2,…,Wk,…Wl),其中Wk为输出层第k个神经元对应的权向量[5]。
对于输出层,
ok=f(netk) ,k=1,2,…,l,
(1)
(2)
对于隐含层有
yj=f(netj) ,j=1,2,…,m,
(3)
(4)
式(3)、式(4)中,转移函数f(x)均为单极性连续可导的Sigmoid函数:

(5)
形成了典型的三层BP神经网络模型。
1.2 人工神经网络的参数以及训练样本的确定
通过参考类似的爆破工艺、且爆破效果良好的矿山爆破资料以及相关文献,以抗压强度、弹性模量、抗拉强度、矿石容重、黏结力以及摩擦角作为BP神经网络的输入因子,以孔底距、炸药单耗、崩矿步距作为输出因子,得到神经网络的训练样本,如表1。
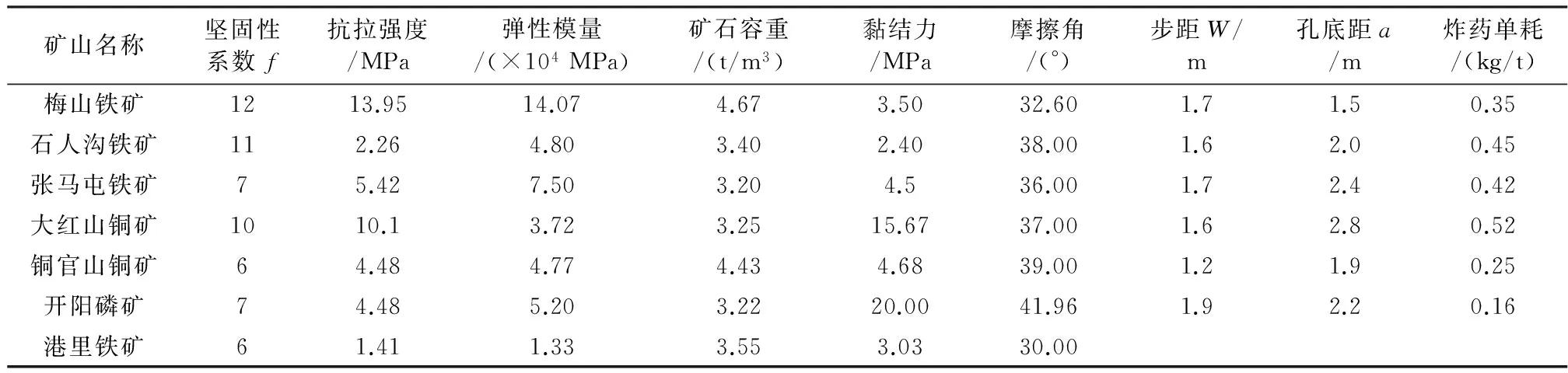
表1 BP神经网络训练样本
1.3 隐含层单元数的确定
本网络设计的输入因子有6个,输出因子3个,计算出隐含层单元个数[6]:
(6)
式中,n为隐含层单元数;m为输入单元数;t为输出单元数;a为1 ~10的数。
通过式(6)计算,得到隐含层单元数为4~13。
建立BP网络模型时,对多种隐含层单元的预测误差进行比对,选出适合的隐含层单元进行优选[7]。为了降低误差提高精度,完全可以通过增加隐含层的神经元个数实现,并且训练效果也比增加隐含层数更容易观察和调整。为了更高效的进行网络训练,选取隐含层单元数为7、9、12,得到以下网络训练误差精度曲线,见图2。

图2 不同单元数的BP神经网络训练精度曲线
通过训练结果可以看出,当神经元个数为9时训练结果最理想,因此初步选定神经元数为9。对根据神经元数为8和10的精度误差曲线进行比较,得到单元数为8和10的训练精度误差曲线图,见图3。

图3 单元数为8、10的BP神经网络训练精度曲线
根据以上不同单元数训练精度曲线图的训练结果,得到以下误差数据,见表2。

表2 不同单元数的训练误差数据
由以上图表可知,当神经元的单元数为9时,误差比较小,精度比较高,因此选择隐含层的神经单元数为9。
1.4 其他参数的确定
由于样本数据各个参数的差异性比较大,为了达到更高的学习效率,需要对样本数据进行归一化处理,归一化后,数据都处在[-1 1]间。BP神经网络隐含层、输出层的神经单元传递函数使用正切函数,得到输出结果后,为了更直观地分析数据,对结果进行反归一化处理。
学习效率的设定在训练过程中发挥着重要的作用,决定每一次循环中权值变化量[8]。较大的学习效率会导致训练的不稳定,较小的学习效率可能会导致网络训练的过程比较长。在现实中,训练往往使学习效率比较小,本文选取的学习效率为0.01。为了使结果更精确,选取样本误差为0.000 1。
当BP神经网络的相关数据以及参数均完成后就可对其进行优选,流程如图4所示。
2 中深孔挤压爆破参数优选影响因素
以BP神经网络模型对港里铁矿的爆破参数进行优选,输入参数6, 1.41,1.33,3.55,3.03,30,对得出的结果数据进行反归一化,得1.723 6,1.827 4,0.49,即港里铁矿中深孔挤压爆破参数的BP神经网络优选参数:炮孔排距W=1.723 6 m,孔底距a=1.827 4 m,炸药单耗q=0.45 kg/t。
(1)对于网络训练样本数据选择的限制性。本文选择的是爆破工艺相类似的、并且爆破效果较为理想的矿山爆破参数为样本,选择的矿山个数以及样本的数据都有一定的局限性。

图4 BP神经网络算法流程
(2)输入层和输出层的数据选取对于训练结果的影响。输入层的数据大多取自矿山的某一水平,而爆破的炮孔步距、孔底距以及炸药单耗可能取自同一矿山的其他开采水平,而实际上不同水平矿岩的性质参数都可能有所变化,从而对优选结果造成影响。输出层的数据并没有包括炮孔直径。
(3)BP人工神经网络模型对训练结果的影响。隐含层是BP神经网络的重要结构之一,过多的隐含层单元数会导致学习时间过长,误差却不一定最小;合理的隐含层神经元数是保证BP网络高效运行的必备条件;而输入层以及输出层函数也对训练结果有一定的影响。
(4)港里铁矿裂隙比较发育,矿岩的稳定性比较差,不经支护无法进行开采,而支护水平的强度大小会影响爆破参数的选取。该矿大多巷道都采用一级或二级支护的“锚网喷”支护形式,支护强度比较高,而选择的部分样本矿山是没有支护的。
综合以上因素对爆破参数进行调整,选取崩矿步距为1.67 m,孔底距为1.8 m,炸药单耗为0.43 kg/t,并在生产过程中根据实际效果作适当的调整。最终所确定的炸药单耗为0.43 kg/t,相对于原来的炸药单耗(0.52 kg/t)降低了17.3%。
3 结 语
采用爆破工艺相似矿山的弹性模量、抗拉强度、抗压强度、摩擦角及黏结力为输入因子,炮孔崩矿步距、孔底距及炸药单耗为输出因子,构成训练样本,得出爆破参数,对于矿山,既节约了爆破实验的成本又提高了效率,有非常大的借鉴意义。
通过BP神经网络的训练,确立了优选爆破参数与影响爆破因子之间的非线性关系;优选的过程中不需要建立数学方程,具有很强的适用性,学习能力比较强;通过此方法,解决一些数据、信息比较少以及很难确定相关关系的问题;避免了传统的爆破参数确定过程中的缺点,具有广阔的应用空间。
[1] 林大泽.降低地下矿深孔爆破落矿大块率的技术措施[J].中国安全科报,2007,17(1):86-90.
[2] 王新民,赵 彬,王贤来,等.基于BP神经网络的凿岩爆破参数优选[J].中南大学学报:自然科学版,2009,40(5):1411-1416.
[3] 夏红兵,徐 颖,宗 琦,等.深部软岩巷道爆破卸压技术及工程应用研究[J].安徽理工大学学报:自然科学版,2007,27(1):13-16.
[4] 张良均,曹 晶,蒋世忠.神经网络实用教程[M].北京:机械工业出版社,2007.
[5] 施 彦,韩力群,廉小群,等.神经网络设计方法与实例分析[M].北京:北京邮电大学出版社,2009.
[6] 葛哲学,孙志强.神经网络理论与MATLABR7实现[M].北京:电子工业出版社,2007.
[7] Homik K, Stinchcombe M, White H. Multilayer feed-forward networks are universal approximator[J].Neural Networks,1989,2(5):359-366.
[8] 王永奇,戴 兵.爆破参数的BP神经网络优选及验证[J].矿业工程研究,2012,27(1):1-3.
Optimization Selection of Medium-deep Hole Blasting Parameters Based on Artificial Neural Network
Xie Jingpeng Ming Shixiang Liang Xinmin
(School of Civil and Environmental Engineering, University of Science and Technology Beijing)
In order to obtain the reasonable medium-deep blasting parameters, taking the ore-bearing rock elastic modulus, bulk density, tensile strength, compressive strength, friction angle and cohesive force as the input factors, taking the hole collapse interval, depth of holes, and consumption of dynamite as the output factors, taking the relative datas of the mines that the blasting technology are similar with each other as the training samples so as to establish the BP neural network model to conduct blasting parameters optimization. Taking the Gangli iron mine as the engineering background, through optimization and analysis of the influence factors to obtain the caving step distance is 1.67 m, the hole bottom distance is 1.8 m, explosive consumption is 0.43 kg/t. The application results show that, the optimized explosive consumption is reduced by 17.3% relative to the original unit explosive consumption(0.52 kg/t).
Medium-deep hole blasting, BP artificial neural network, Optimization selection
2014-11-08)
谢经鹏(1989—),男,硕士,100083 北京市海淀区学院路30号。

