预裂缝充水对减震效果的影响分析

巫雨田 房泽法

(1.紫金矿业集团股份有限公司紫金矿冶设计研究院；2.武汉理工大学资源与环境工程学院)

预裂缝充水对减震效果的影响分析

巫雨田1房泽法2

(1.紫金矿业集团股份有限公司紫金矿冶设计研究院；2.武汉理工大学资源与环境工程学院)

运用ANSYS/LS-DYNA软件对预裂缝中不同充水高度时的台阶爆破进行数值模拟，获得平均减震率，通过对平均减震率随预裂缝中充水高度变化规律的分析，得出：预裂缝充水高度小于0.4倍预裂缝深度时，预裂缝充水对减震效果的影响不大；预裂缝充水高度大于0.4倍预裂缝深度时，随着充水高度的增加，减震效果下降迅速。结论对预裂爆破工程减震效果具有科学的指导意义。

台阶爆破 数值模拟 充水预裂缝 减震效果

台阶爆破中，常采用预裂爆破控制主爆炮孔爆破对保护岩体及周围建构筑物的破坏。由于主爆炮孔是在预裂孔起爆后才起爆，当爆区水文地质条件复杂或遇到雨水天气时，预裂缝中可能充水。预裂缝充水后，地震波中的纵波会直接透射过水层进入到预裂缝后方的保留岩体，使得预裂缝的减震效果变差。目前，有些学者主要从理论分析的角度对充水预裂缝作用机理及其对减震的影响进行研究[1-2]。然而，由于岩体是一种非均匀非连续的介质，这种结构造成了应力波动性质变化多端，很难用理论方法精确地描述裂隙岩体的应力波动[3]。有些学者采用数值模拟的方法对预裂缝(减震沟)的减震效果进行了研究，并用数值模拟的结果指导工程实践，取得了一定的成果[4-6]。本文以小型采石场台阶爆破为基础，采用有限元动力分析软件ANSYS/LS-DYNA建立预裂缝中不同充水高度时的数值模型，探究预裂缝不同充水高度对减震效果的影响。

1 充水预裂缝数值模型建立及计算

1.1 数值计算模型及材料参数

以小型采石场台阶爆破为例，建立数值计算模型，见图1。模型总体高18 m，长65 m，宽28 m。采场台阶高7 m，炮孔直径为90 mm，孔深8 m，装药长度为5 m，填塞长度为3 m，最小抵抗线为3 m。预裂缝距炮孔10 m，预裂缝深10 m，长20 m，宽10 cm，预裂缝中充填水高度取0(即缝中无水)，2，4，6，8和10 m(即缝中充满水)，共建立6个数值计算模型。地表面、边坡面及预裂缝处为自由边界，不施加任何约束；模型的4个侧面和底面为无反射边界。由于炮孔形状仅对炮孔附近局部范围内岩石的力学参数有影响，对于研究离炮孔较远处测点的爆破震动情况没有影响，因此，为方便网格划分，提高计算精度，用方形炮孔代替圆形炮孔进行模拟。

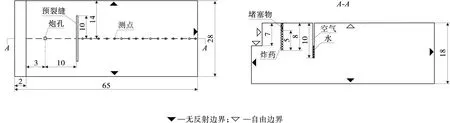
图1 充水预裂缝数值计算模型示意(单位：m)

由于炮孔位于台阶宽度的中心线上，为提高网格划分精度，节省计算资源，只需建立与炮孔轴线相对称的1/2模型，并在对称面上施加对称约束。炸药网格划分尺寸为0.02 m×0.2 m，预裂缝(即缝中的空气和水)网格划分尺寸为0.02 m×0.4 m，岩石网格划分尺寸为0.4 m×0.4 m。三维模型网格划分见图2。

图2 三维实体建模(1/2模型)网格划分

1.2 材料参数及数值计算算法

为模拟爆破产生的地震波，使用LS-DYNA中的爆轰模拟功能。爆炸对围岩产生的压力作用采用爆轰过程的JWL状态方程来模拟，其表达式为

(1)

式中,P为爆炸产生的压力，GPa；V为爆轰产物的相对体积；A、B、R1、R2和ω为炸药材料常数；E0为初始比内能,GPa。炸药的主要材料参数见表1。

表1 炸药材料参数

岩石采用各向同性的随动硬化塑性材料。这种材料非常有效，且适合实体单元。岩石材料参数见表2。

表2 岩石材料参数

水的状态方程：

(2)

式中，P为水受到的压力，MPa；ρ0为水的密度，kg/m3；γ0为Grunesien系数；α为对系数γ0的一阶体积修正；E为初始内能，GPa；C为VS-VP曲线截距；S1、S2、S3为VS-VP曲线斜率的系数；μ为材料系数，ρ/ρ0-1，ρ为水的当前密度，kg/m3。

水的材料参数见表3。

表3 水材料参数

空气的状态方程：

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E，

(3)

式中，P为空气所受压力，MPa；C0、C1、C2、C3、C4、C5、C6为常数；E为单位介质体积内能，GPa；μ为材料系数，ρ/ρ0-1，ρ为空气当前密度，kg/m3，ρ0为空气初始密度，kg/m3。

为方便计算，一般将空气看作理想气体，则空气的材料参数见表4。

表4 空气材料参数

炸药采用Euler算法，岩石、空气、水均采用Lagrange算法。采用流固耦合方式处理炸药与岩石间的相互作用，采用共节点方式处理岩石、空气、水间的相互作用。

1.3 测点布置

如图1，测点布置于预裂缝的右侧A-A剖面与地表的交线上，第一个测点离预裂缝的距离为2 m，第二个测点离缝距离为6 m，依次类推，每隔4 m取一个测点，最后一个测点离预裂缝的距离为50 m。

2 数值模拟结果及分析

2.1 缝后质点振速衰减规律分析

根据模拟得到的质点振速时程曲线，获得各测点质点峰值振动速度。如图2，定义X轴方向为水平径向，Z轴方向为垂直方向，Y轴方向为水平横向。数值模拟结果显示，与水平径向和垂直方向相比，水平横向的质点峰值振速非常小，因此，本文只对质点水平径向及垂直方向的峰值振速变化进行分析。不同工况下各测点水平径向及垂直方向质点峰值振速见表5和表6。

表5 预裂缝不同充水高度时不同测距的质点水平径向峰值振速

注：有、无预裂缝测点的选取是一一对应的，即相对应测点到爆源的距离是相同的。

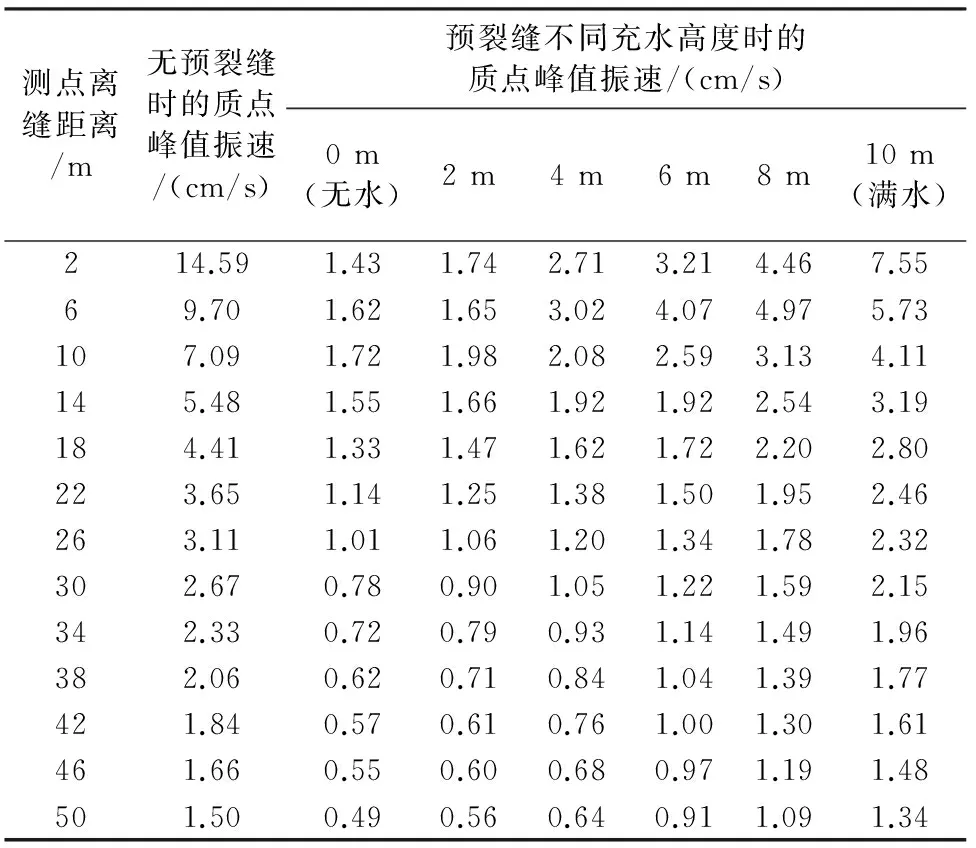
表6 预裂缝不同充水高度时不同测距的质点垂直方向峰值振速

注：有、无预裂缝测点的选取是一一对应的，即相对应测点到爆源的距离是相同的。

根据表5、表6拟合出无预裂缝、无水预裂缝及预裂缝充水10 m时质点峰值振速的衰减规律曲线，见图3。

图3 质点峰值振速衰减规律拟合曲线

引入比例距离，即

(4)

式中，Q为最大单响起爆药量，kg；R为测点到爆源的距离，m。

对无预裂缝时水平径向及垂直方向的质点峰值振速按萨道夫斯基公式拟合如下：

水平径向为

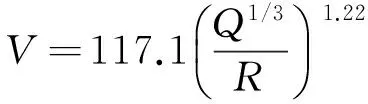
(5)

垂直方向为

(6)

式(5)和式(6)拟合的相关系数均大于99%。无预裂缝时质点峰值振速的衰减规律完全符合萨道夫斯基公式(比例距离在3.33～16.63 m/kg1/3)。

对预裂缝(10 m深)无水情况下的质点峰值振速衰减规律按萨道夫斯基式公式进行拟合，结果如下：

水平径向为

(7)

垂直方向为

(8)

式(7)拟合的相关系数为0.81，式(7)拟合的相关系数为0.83，均低于85%，因此，无水预裂缝的存在使得缝后质点峰值振速的衰减规律不再符合萨道夫斯基公式。

对充水10 m预裂缝的质点峰值振速衰减规律按萨道夫斯基公式进行拟合，结果如下：

水平径向为

(9)

垂直方向为

(10)

式(9)、式(10)拟合的相关系数均大于99%。因此，当预裂缝充满水后，缝后质点峰值振速的衰减规律依旧符合萨道夫斯基公式。

比较无预裂缝、有预裂缝和预裂缝中充满水时的拟合公式，发现充满水的预裂缝缝后质点峰值振动速度的衰减系数和衰减指数均小于无预裂缝时的值，但大于预裂缝中无水时的值，与无水预裂缝相比，充满水的预裂缝降震效果明显降低。

2.2 预裂缝充水高度对减震效果的影响分析

为了研究预裂缝内不同充水高度对降震效果的影响，定义减振率η为

(11)

式中，vw为无预裂缝时质点振速，m/s；vy为有预裂缝(或裂缝充水)时质点振速，m/s。

由表5、表6、式(11)计算出预裂缝充水高度与减震率的关系，结果见表7和表8。

表7 预裂缝不同充水高度时不同测距的质点水平径向减震率

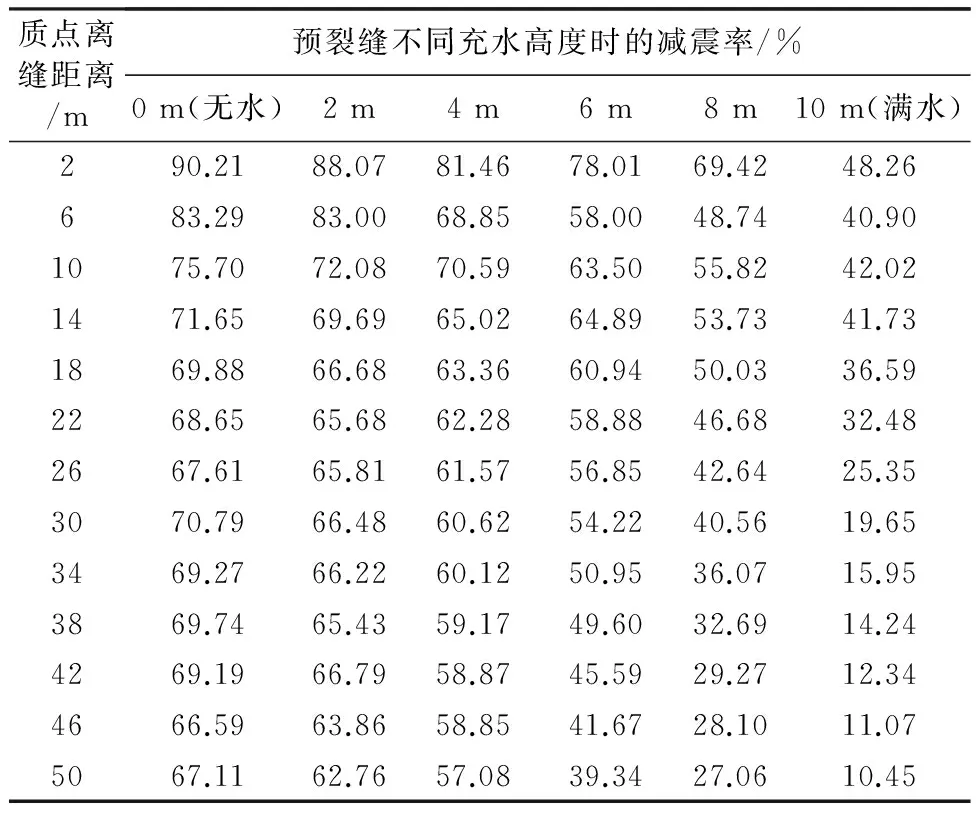
表8 预裂缝不同充水高度时不同测距的质点垂直方向减震率

从表7和表8可以看出，离预裂缝较近范围内质点的振速变化较为紊乱，为寻找预裂缝内充水高度与降震率的规律，只取离缝10 m之外的测点。将这些测点的减震率求平均值，其结果见表9。

表9 预裂缝充水不同高度时平均减震率

从表9可以看出，与无充填水预裂缝相比，当预裂缝中充填2 m深的水时，水平径向减震率降低约4%，垂直方向减震率降低约3%；当预裂缝中充填10 m深的水(即缝中充满水)时，水平径向减震率降低约50%，垂直方向减震率降低约46%。

根据表9，作出平均减震率随预裂缝充水高度增加的变化曲线，对变量预裂缝充水高度进行无量纲化，以充水高度H与预裂缝深度L1的比值作为曲线图的横坐标，见图4。

从图4可以看出，当H/L1<0.4时，随着充水高度的增加，减震率由80.71%降至71.42%，下降缓慢，在该范围内预裂缝充水对减震效果的影响不大；当H/L1>0.4时，随着充水高度的增加，减震率下降迅速。因此，工程实际中应避免预裂缝充水的高度大于0.4倍预裂缝深度。

运用Matlab软件对图4中的曲线进行拟合，令x=H/L1，得出水平径向和垂直方向平均减震率η与H/L1的关系，如下式：

图4 平均减震率随预裂缝充水高度的变化规律

水平径向为

η=-11.06e1.71x+92.26 .

(12)

垂直方向为

η=-7.52e1.97x+77.57 .

(13)

上式拟合的相关系数均大于0.95，因此采用式(12)和式(13)表示平均减震率η与H/L1的关系是可取的。

3 结 论

(1)预裂缝充满水后，缝后质点峰值振速的衰减规律依旧符合萨道夫斯基公式，但衰减系数和衰减指数均小于无缝时的值，与无水预裂缝相比,充满水的预裂缝降震效果明显降低。

(2)预裂缝充水高度小于0.4倍预裂缝深度时，随着充水高度的增加，减震率下降缓慢，在该范围内预裂缝充水对减震效果的影响不大；当预裂缝充水高度大于0.4倍预裂缝深度时，随着充水高度的增加，减震效果下降迅速。因此，工程实际中应避免预裂缝充水高度大于0.4倍预裂缝深度。

[1] 卢文波，赖世骧，董振华．岩石钻爆开挖中预裂缝的隔震效果分析[J]．爆炸与冲击，1997，17(3)：193-198．

[2] 张志呈，肖正学，张渝疆，等．工程爆破地震波的裂隙效应[J]．西南科技大学学报：自然科学版，2004，19(3)：57-60．

[3] 鞠 杨，环小丰，宋振铎，等．损伤围岩中爆炸应力波动的数值模拟[J]．爆炸与冲击，2007，27(2)：136-142．

[4] 余德运，杨 军，赵明生．减震沟对台阶爆破地震波减震机理探讨[J]．煤炭学报，2011，36(2)：244-247．

[5] 王幸荣．预裂缝减振效果研究[D]．武汉：武汉理工大学，2006．

[6] 方 向，高振儒，龙 源，等．减震沟对爆破震动减震效果的实验研究[J]．工程爆破，2002，8(4)：20-24．

Analysis of the Influence of Pre-splitting Fissure Water Filling to Damping Effects

Wu Yutian1Fang Zefa2

(1.Zijin Design and Research Institute of Mining and Metallurgy, Zijin Mining Group Co., Ltd.;2.School of Resources and Environmental Engineering, Wuhan University of Technology)

The bench blasting process of the different water filling height in pre-splitting fissure is simulated by ANSYS/LS-DYNA software, the average damping rate is obtained. The change rule of the average damping rate with the water filling height in pre-splitting fissure is analyzed in depth, the results show that the water filling height is lower than the depth of pre-splitting fissure of 0.4 times, the influence of water filling in pre-splitting fissure is little; otherwise, with the increase of water filling height, the damping effects decreased rapidly. The above conclusion has the guidance significance of the damping effect of pre-splitting engineering.

Bench blasting, Numerical simulation, Water filling pre-splitting, Damping effect

2015-03-07)

巫雨田(1990—)，男，助理工程师，硕士研究生，364200 福建省龙岩市上杭县北二环紫金矿业学院C栋320。