瓶颈通行权交易制度的研究进展

王鹏飞，徐秋实，唐克双

(1.河北科技师范学院城市建设学院，河北秦皇岛066004；2.日本国立东北大学研究生院信息科学研究科，宫城仙台9808579；3.燕山大学建筑工程与力学学院，河北秦皇岛066004；4.同济大学交通运输工程学院，上海201804)

0 引言

伴随城镇化进程的不断加快，机动车的急速增长使得交通供需矛盾进一步加剧。近年来，国内外交通学者主要从“价格控制”和“数量控制”两个方面对解决交通拥堵问题的策略进行研究[1-2]。前者的代表性研究主要为拥挤收费政策[3]，其存在的问题是道路管理者一旦根据错误的交通需求函数来制定价格，就会发生社会福利损失，而在现实生活中，道路管理者对出行者交通需求函数的正确把握是几乎不可能的。后者的代表性研究主要为交通流入量控制[4]，此类研究虽然不需要把握出行者的交通需求函数，但由于它限制了出行者的自由选择权利(例如希望到达目的地时间、出行路径等)，所以也会产生相应的社会福利损失。因此，如何构建既不需要把握出行者需求函数，又可以保障出行者自由选择权利的交通治堵方案成为交通学者研究的重点。

瓶颈通行权交易制度(Tradable Bottleneck Permit，TBP)就是在这一背景下由Akamatsu等人提出[5]。本文从TBP的基本概念着手，对近几年的相关研究成果进行总结，并对后续待研究问题进行展望。

1 制度的提出

经过长期研究，Akamatsu等人提出了既能够保障出行者自由选择权，又不需要把握出行者需求函数的新型交通政策“瓶颈通行权交易制度”。此制度是指在指定的交通瓶颈，在指定的时段内才能通过的权利。根据Akamatsu等人在研究中所设定的理想状态，制度导入之后的均衡状态与社会最优状态(即帕累托最优)是一致的。出行者可以通过以下两种绝对公平的方式获得通行权：一种是道路管理者按照一定的周期对所有出行者进行免费的轮回发放；另一种是通过某种方式建立具有完全竞争性质的通行权交易市场，出行者可以通过与道路管理者的交易获得通行权。最后，经Akamatsu等人[5]的论证，得出无论哪种方式均可使得制度导入后的均衡状态与社会最优状态相一致的结论[5]。

研究对象的交通网络构成如图1所示，在居住区与目的地之间，存在唯一的交通瓶颈，其通行能力为μ，所有出行者在通勤的过程中都要经过此交通瓶颈。若利用累积图对瓶颈上游的车辆到达与瓶颈下游的车辆流出进行分析，则会得出如下结论：1)制度导入前，每个出行者的总时间损失为排队等待时间(Traffic Queue Delay)与日程损失时间(Schedule Delay)之和(见图 2a)；2)制度导入后，可看出等待排队时间由于TBP的导入消失了，每位出行者只剩下日程损失时间(见图2b)。达到均衡状态后，每位出行者均没有改变自己出行时间的动机。此外，对于通行权交易制度与静态、动态的交通拥挤收费政策在经济学原理上的区别已经由文献[6]进行了比较及论证。

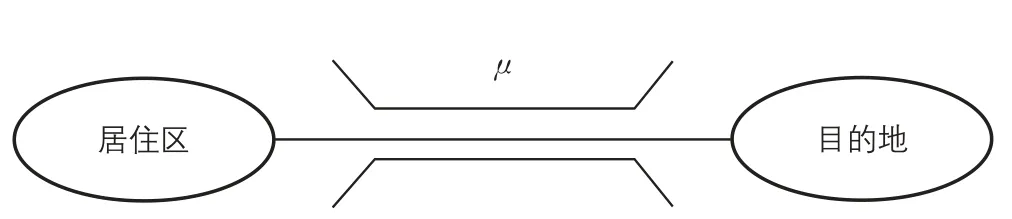
图1 交通网络的设定Fig.1 Schematic diagram of transportation network

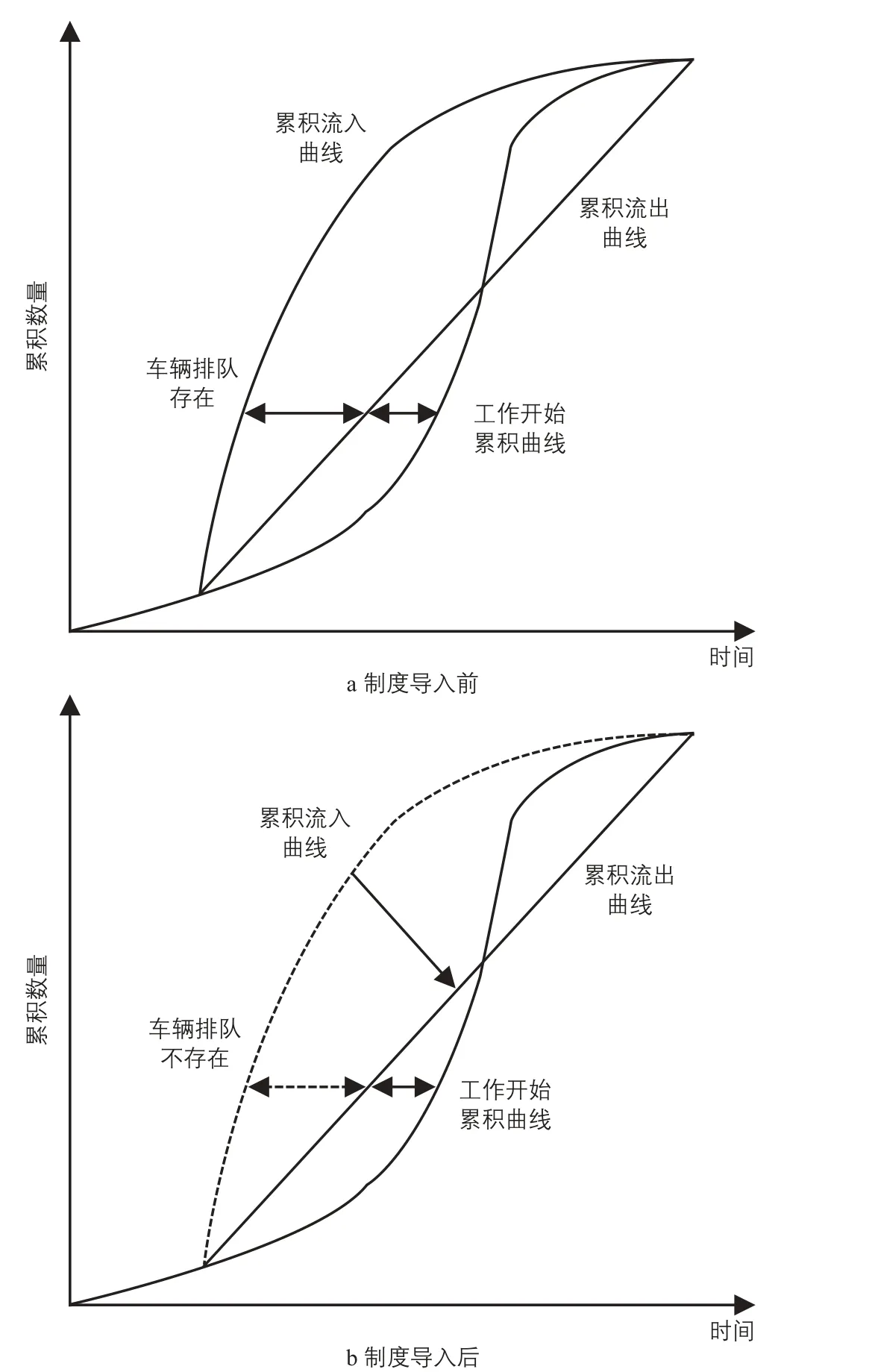
图2 瓶颈通行权交易制度导入前后的车辆累积数量Fig.2 Number of vehicles accumulated before and after TBP system is introduced

2 相关研究的扩展

2.1 出行者随机到达条件下的最优通行权发行方式

在基础研究中，Akamatsu等人假设所有出行者均完全按照通行权指定的时间到达交通瓶颈[5]。在这种状态下，制度导入之后的均衡状态与社会最优状态是完全一致的。而在现实生活中，这种假设往往很难实现，出行者极容易出现比指定时间“早到”或“迟到”的现象。而道路管理者若依然按照“瓶颈通行能力等于通行权发放数量”这一原则进行操作，则在同一时段内到达瓶颈的出行者数量就有可能超过瓶颈的通行能力从而形成等待队列。

对此，文献[7]与文献[8]认为每位出行者都会竭尽全力地按照通行权指定的时间到达交通瓶颈。研究者认为每位出行者实际到达交通瓶颈的时间符合以通行权指定到达时间为均值的正态分布。基于此，研究中可利用Fokker-Planck方程式对车辆排队长度的实时变化进行描述[9]，在给定外生的通行权发行函数的情况下，通过计算验证最优通行权发行方式的存在性。即存在一种通行权发行方式，它可以使得所有出行者的等待队列时间损失加上日程时间损失之和最小。

文献[8]又通过数值计算寻找到不同出行者特性组合(时间价值、风险回避率等)之下的最优通行权发行方式。即在外生线性函数的基础上扩展到幂函数(幂指数分为大于1与小于1两种情况考虑)、Logistic函数。

2.2 网络通行权交易制度

在将研究对象由单一的交通瓶颈推广到整个交通网络之前，文献[10]先以串联的两个瓶颈为研究对象，研究了制度导入后是否可以实现交通网络费用的最小化以及是否可以实现帕累托最优的两个问题。最后，得出制度导入后一定可以实现交通网络费用的最小化以及道路管理者若不将通行权费用用于投资瓶颈的通行能力改善，则不一定达到帕累托最优的结论。

在此基础之上，文献[11]以一般交通网络为研究对象提出了网络通行权交易制度(Tradable Network Permit,TNP)，即在特定时段通过特定路段的权利。如此，则在任一时段内，路段上的车流量都不会超过路段通行能力，即不会发生交通堵塞现象。进而，推导出制度导入之后的均衡状态与交通网络费用最小状态相一致的结论。最后，证明在弹性OD需求、出行者工作开始时间按照一定概率分布的一般状况设定下上述结论的适应性。

2.3 基于进化博弈理论的TNP自律分散实施方法

在网络通行权交易制度研究中，关于TNP实施方法的两个问题尚未被提及：一个是任一初始状态将通过怎样的过程才能够达到文献[11]所提及的均衡状态；另一个是TNP(既要确定时间，又要确定路径，与TBP不同)烦琐的手续可能会使得出行者望而生畏，使得制度的可实施性降低。

为解决上述两个问题，文献[12]在智能交通系统(Intelligent Transportation Systems,ITS)与信息通信技术(Information and Communication Technology,ICT)硬件发展的基础之上，提出在每辆车上都安装Agent软件，通过Multi-agent系统代理出行者完成TNP交易复杂手续的设想以增加制度的可实施性。其中，每条路段、每个时段的交通流与通行权的价格也是由所有Agent的微观行动聚集在一起所决定的(道路管理者和任一Agent都没有决定通行权价格的能力)，通过动态的进化过程，最终收敛于均衡状态(所有Agent都没有更改自己当前选择动机的状态)。即任一初始状态都将通过一定的动态过程达到均衡状态，并且所达到的均衡状态与社会最优状态一致。

2.4 TBP与TNP的交易市场原理设计

在TBP的基础研究中，Akamatsu等人对出行者获得通行权的方式设定了免费发放与市场交易两种。但在应对出行者数量较多、出行时间较为固定且居住较为分散的状态时前者就显得力不从心了，因此，出行者主要还是通过市场交易来实现通行权的购入。根据Akamatsu等人[5]最初提出的设想，通行权交易市场应为没有垄断现象出现的完全竞争市场，而具备这种性质的交易市场在现实生活中是不常见的。

对此，文献[13]与文献[14]创造性地提出利用拍卖理论(Auction Theory)来构建通行权交易市场的设想，即利用文献[15]提出的VCG拍卖机制实现：若某时段的通行权价格不为零，则此时段内交通需求必大于等于瓶颈通行能力；若价格为零，则此时段内的交通需求必小于瓶颈通行能力。每个出行者可以根据自身的意愿支付能力、时间价值来选择不同时段的通行权，即出行者个人效用最大化，最终达到所有出行者都没有改变自己选择动机的均衡状态。但VCG拍卖机制的劣势在于很容易出现出行者所申报的意愿支付能力与大众不符，脱离实际的奇怪现象。对此，文献[13]提出利用文献[16]多物品升值拍卖理论即可解决上述问题的设想。出行者根据自身的意愿支付能力、时间价值，以及不断变动的通行权价格去寻找对于自身效用最大的通行权时段。

同时，文献[17]又对交通需求不确定下的通行权交易市场进行分析，认为在道路管理者已知通行权购买者“退票率”的情况下，通过对交易市场中各时段的通行权数量进行管理，也可使得实现的均衡状态与社会最优状态相一致。此外，还提出一种“试错(Trial and Error)”方式来寻找出行者“退票率”，即道路管理者在初始时不知道出行者“退票率”的状态下，通过上述的试错方式最终实现社会最优状态的方法，并通过理论及数值试验证明了此方式的可行性。

按照TNP市场交易原理进行设计时的难点为：由于存在出行者的路径选择，因此道路管理者很难同时对路径(Path)容量与路段(Link)容量进行把握。对此，文献[18]提出如下设想：在第j天，道路管理者首先将每条路径的通行权数量固定，然后再让出行者根据自身特性进行出行时段的选择；在第

j+1天，道路管理者根据第j天所获得的各路径交通量与各时段的通行权价格对每条路径的通行权数量进行调整(见图3)，之后再让出行者根据自身特性进行出行时段的选择。如此往复数次，在有限的天数内，就可以使得路网的交通量分配达到社会最优状态。此设想与Benders分解算法[19]求解混合整数规划问题的流程是一致的，即将文献[18]中建立的社会最优化问题的数学模型定义为路径容量是连续变量，而出行者是否拥有此路径的通行权是0-1整数变量的混合整数规划问题。

通过拍卖理论建立起来的通行权交易市场有两点特性：所有出行者在报价时都不存在虚假报价的动机(即所报价格都反映出行者的真实意愿支付能力)；通过提出的“逐日(Day-to-Day)”调整战略方式，道路管理者可以在有限的时间内使得实现的均衡状态与社会最优状态相一致。此特性已经通过文献[13]，[14]以及[18]得到严格证明。

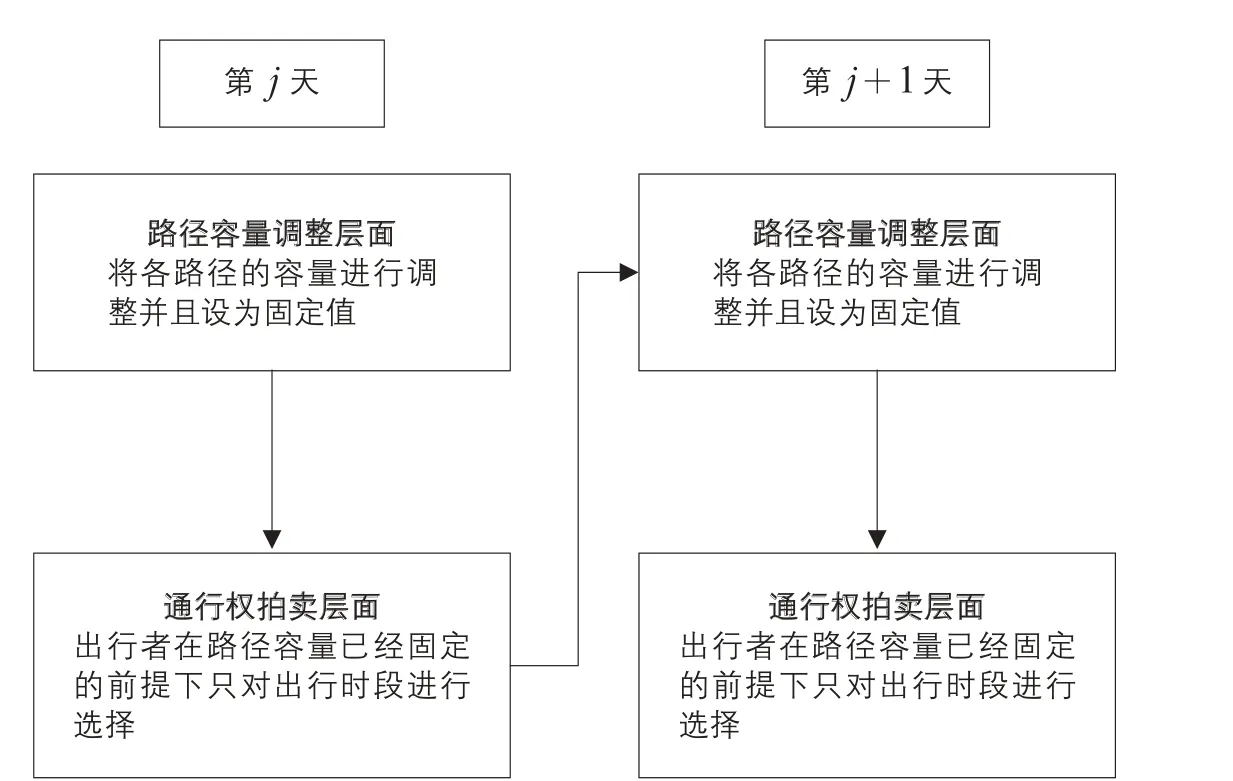
图3 “Day-to-Day”的进化型调整方式Fig.3 Day-to-Day evolutionary adjustment mode

2.5 多个交易时间点的TBP市场原理设计

现实中，出行者在统一规定的时间点内集合到通行权交易市场来购买通行权的情况几乎不太可能，一定会有部分出行者在不同的交易时间点购买同一时段通行权。特别是节假日的观光旅游，提前预订通行权以避免交通拥堵是出行者的心理之一。

针对这一问题，文献[20]提出设定多个通行权交易时间点，并通过调整各个交易时间点的通行权销售总量来实现社会最优状态的设想。但由于出行者在各个交易时间点的意愿支付能力具有变动性，且道路管理者对此无法把握，因此，也必须通过借鉴前述提及的“Day-to-Day”动态进化战略调整方式来不断地对各个交易时间点的通行权数量进行调整以实现社会最优状态。文献[20]根据其所设定的状况，将此方式命名为“逐周(Week-to-Week)”战略调整方式(见图4)，其中各个时间点的通行权销售数量调整层面与2.4节所述路径容量调整层面相对应。

2.6 基于TNP的自律分散信号控制

对于某一特定的交通瓶颈，道路管理者利用不停车电子收费系统(Electronic Toll Collection,ETC)可以方便地实现对通行权持有者的识别、控制。但对于相对复杂的城市道路网络以及ETC尚未普及的城市中心区域而言，若再利用ETC系统会在很大程度上限制TNP的可操作性。因此，在城市道路网络中，利用现有的交通管控设施以实现对通行权持有者的识别、控制是研究的重点。

对此，文献[21]提出以平面交叉口的交通信号灯作为TNP具体实施载体的设想。道路管理者以一个固定信号周期的交叉口实际通行能力为通行权发行数量的最大值，对不同进口道与出口道组合(即车辆不同行驶方向)的通行权分别设定交易市场，而这些交易市场对于同一时段的通行权数量之和不得超过上述的最大容量(实际中采用的饱和度不应超过0.9)。道路管理者通过调整各相位的绿信比来控制通行权的发行量，而通过通行权的销售量与价格来对信号控制方案进行调整。如此，道理管理者就可以通过交通信号灯实现对通行权持有者的识别与控制(见图5)。

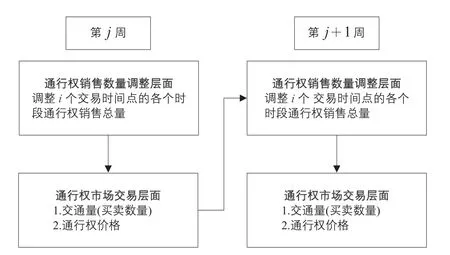
图4 “Week-to-Week”的进化型调整方式Fig.4 Week-to-Week evolutionary adjustment mode

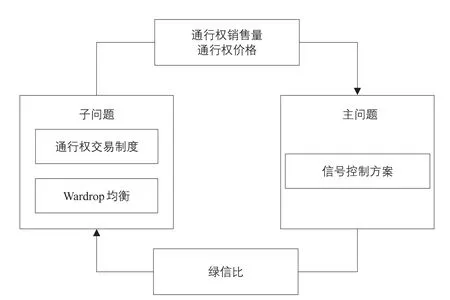
图5 基于TNP的自律分散信号控制Fig.5 TNP-based autonomous decentralized signal control

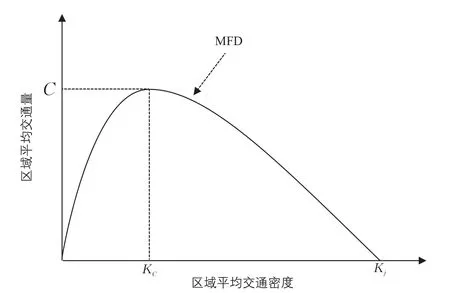
图6 宏观基本图Fig.6 Macroscopic fundamental diagram

2.7 基于MFD与TBP的区域流入控制

在上述研究中，文献[11]假设研究对象交通网络中的每条路段均被导入通行权制度。若对于比较简单的高速公路网络，此假设尚有可能成立，而对于相对复杂的城市道路网络则显得不尽实际。因此，只考虑在部分路段导入TBP的措施十分可行。

随着对交通拥堵问题的研究对象从孤立的点向把小区作为基本单位转变，并最后转移至整个交通网络上来，人们发现大城市中存在着宏观基本图(Macroscopic Fundamental Diagram,MFD)[22]。文献[23]在 2007 年最早提出MFD概念，并在随后的研究中给出MFD一种描述性定义，认为它可以描述网络中移动的车辆数和网络运行水平之间的关系，也可以用于描述平均交通量与平均交通密度的普遍关系(见图6)，同时在著名的日本横滨试验中，通过固定检测器和浮动车两种方法采集到的数据均验证了大城市中MFD的存在[24]。

在MFD理论的基础上，文献[25]提出通过TBP的部分导入实现重点区域的流入控制，例如CBD及城市中心易拥堵区域(见图7)。具体做法为：首先，将易拥堵区域画出，在区域所有的出入口处设置通行权检测器(在区域内部与外部均不设置，即实现部分导入)。其次，在区域内部各路段的适当位置设置检测器，以便对区域内的平均交通密度进行实时监控。最后，道路管理者通过通行权销售数量来控制区域流入量，使得区域内的平均交通密度维持在一个最理想的范围之内。这对于防止区域内部交通量出现超饱和现象具有十分重要的意义。

3 结语

自从Akamatsu等人提出TBP理论之后，众多交通学者针对TBP展开多角度的研究并取得不少成就，但以下5方面问题尚值得进一步探究。

1）虽然有学者利用Fokker-Planck方程式对队列等待长度进行模拟，通过数值计算推导出最优瓶颈通行权发行方式的存在性，但研究自始至终都是应用理论分析与数值试验的手法，而在政策具体实施之前，还需要有交通微观仿真实验结果的支持。

2）对于一般交通网络，在考虑出行者随机到达的条件下，通过模型进行理论分析来推导出最优通行权发行方式是十分困难的。因此，还需要采用交通微观仿真的手法对TNP实施后的网络运行状态进行全面分析，以寻找出最优通行权发行方式，这也是现阶段唯一的可行方法。

3）在基于TNP的自律分散信号控制理论中，文献[21]对到达交叉口车辆的时间间隔进行限制，假定在交叉口处等待的车辆只有固定时间延误，而没有随机时间延误，这一假设与TBP基础研究中的理想状态一致。因此，在考虑车辆随机到达(即考虑车辆随机延误)的条件下，既往研究中提出的信号控制方案是否还能保持原有的特性需要进一步讨论。

4）在基于MFD与TBP的区域流入控制理论中，文献[25]假设区域内产生的车辆对MFD没有影响。但在实际生活中，这种假设不一定成立。通行权发行数量需要根据区域中现有机动车数量与区域内部交通观测数据进行实时调整，因此，在考虑区域内部交通发生量的基础上如何进行通行权发行量的调整将是未来研究的重点。

5）TBP作为交通量控制的一种方式，其应用不应仅仅局限于对动态交通的控制。例如，文献[26]就将此思想应用于停车控制领域并取得了成就。因此，未来若能够将瓶颈通行权交易理论应用于有关流量控制的其他领域将会获得更多收获。

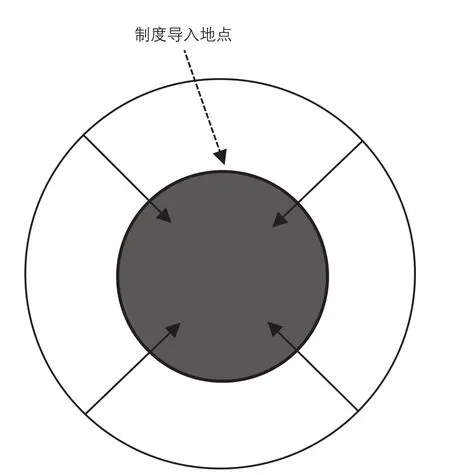
图7 目标区域与TBP实施位置Fig.7 Target area and the location of TBP implementation

[1]Laffont J J.More on Price vs.Quantities[J].The Review of Economic Studies,1977,44:177-182.

[2]Weitzman M L.Price vs.Quantities[J].The Review of Economic Studies,1974,41:477-491.

[3]YangH,HuangHJ.MathematicalandEconomic Theory of Road Pricing[M].Holland:Elsevier,2005.

[4]Akahane H,Kuwahara M,Sato T.A Basic Study on Trip Reservation Systems for Recreational Trips on Motorways[J].Journal of JSCE,2000,49:79-87.

[5]Akamatsu T,Sato S,Nguyen X L.Tradable Time-of-Day Bottleneck Permits for Morning Commuters[J].Journal of JSCE-D,2006,62(4):605-620.

[6]FangY,Wang PF,Huang J F,Meng D G,Wang Z S.A Comparative Study of the Tradable Bottleneck Permits Scheme and Congestion Pricing Policy[C]//International Conference on Communication Technology and Application.Piscataway,N.J.:IEEE,2011:949-953.

[7]Kasahara Y,Akamatsu T.Optimal Time-Dependent Patterns of Bottleneck Permits with Stochastic Queues[C]//Proceedings of Infrastructure Planning(CDROM).Tokyo:JSCE,2006:130.

[8]Wang P F,Akamatsu T,Wada K.Optimal Time-Dependent Patterns of Bottleneck Permits under Stochastic User Arrival[C]//Proceedings of Infrastructure Planning(CDROM).Tokyo:JSCE,2014:232.

[9]Newell,G F.Application of Queuing Theory[M].London:Chapman and Hall,1971.

[10]Yodoshi M,Akamatsu T.Pareto Improvement Properties of Tradable Permits Systems for Tandem Bottleneck Networks[J].Journal of Infrastructure Planning Review,2008,25(4):897-907.

[11]Akamatsu T.A System of Tradable Bottleneck Permits for General Networks[J].Journal of JSCE-D,2007,63(3):287-301.

[12]Kikuchi S,Akamatsu T.Dynamics of Decentralized Multi-AgentSystemsforImplementing Tradable Network Permits[J].Journal of Infrastructure Planning Review,2008,25(3):589-596.

[13]Wada K,Akamatsu T.An E-market Mechanism for Implementing Tradable Bottleneck Permits[J].Journal of JSCE-D,2010,66(2):160-170.

[14]Wada K,Akamatsu T,Nagae T.Stochastic Convergence ofRoad User'sLearning Process under a Hybrid Scheme of Tradable Bottleneck Permits and Congestion Pricing[C]//Proceedings of Infrastructure Planning(CD-ROM).Tokyo:JSCE,2010:84.

[15]Vickrey W.Counter Speculation,Auction,and Competitive Sealed Tenders[J].The Journal of Finance,1961,16:8-37.

[16]Demange G,Gale D,Sotomayor M.Multi-Item Auctions[J].Journal of Political Economy,1986,94:863-872.

[17]Nagae T,Gai N.Tradable Bottleneck Permits under Demand Uncertainty[C]//14thHong Kong Society for Transportation Studies.Hong Kong:HKSTS,2009:771-776.

[18]Wada K,Akamatsu T.Auction Mechanisms for Implementing Tradable Network Permit Markets[J].Journal of JSCE-D3,2011,67(3):376-389.

[19]Tone K.Mathematical Programming[M].Tokyo:Asakura Publication,2007.

[20]Wang P F,Wada K,Akamatsu T.Trading Mechanisms for Bottleneck Permits with Multiple Time Purchase Opportunities[C]//Proceedings of Infrastructure Planning(CDROM).Tokyo:JSCE,2010:167.

[21]Wada K,Akamatsu T.Distributed Signal Control based on Tradable Network Permits:Designand Evolutionary Implementation[C]//Proceedings of Infrastructure Planning(CD-ROM).Tokyo:JSCE,2011:116.

[22]Liao D B,Ma W J.Reviews of the Macroscopic Fundamental Diagram[C]//7thChina Intelligent Transportation Conference Excellent Proceedings.Beijing:CITSA,2012:3-8.

[23]Daganzo C F.Urban Gridlock:Macroscopic Modeling and Mitigation Approaches[J].Transportation Research Part B,2007,41(1):49-62.

[24]Geroliminis N,Daganzo C F.Existence of urban Scale Macroscopic Fundamental Diagrams:Some Experimental Findings[J].Transportation Research Part B,2008,42(9):759-770.

[25]Wada K,Akamatsu T.An Area Metering Control based on Tradable Bottleneck Permits[C]//Proceedings of Infrastructure Planning(CD-ROM).Tokyo:JSCE,2012:113.

[26]Zhang X N,Yang H,Huang H J.Improving Travel Efficiency by Parking Permits Distribution and Trading[J].Transportation Research Part B:Methodological,2011,45(7):1018-1034.