行波效应对大跨度斜拉桥的随机地震响应分析

罗泽辉

(中铁二院工程集团有限责任公司，成都　610031)

工学硕士。

行波效应对大跨度斜拉桥的随机地震响应分析

罗泽辉

(中铁二院工程集团有限责任公司，成都610031)

摘要：大跨度斜拉桥各支承之间距离较大，地震波的传播速度有限，地震波到达各支承的时间存在差异，因此采用一致激励分析方法与实际情况不符。以某大跨度斜拉桥为算例，其主跨为680 m，建立数值有限元模型。主要分析主梁与主塔在单维及多维随机地震动激励下，同时考虑行波效应的地震响应规律，并作了对比分析。结果表明：与一致激励相比，当视波速为200 m/s与300 m/s时，纵向地震动激励下，主梁跨中纵向位移分别减小了42.3%和44.8%，横向地震动激励下，1号塔和2号塔柱底部的竖向弯矩分别减小了25.9%、19.9%和0.4%、1.2%。多维地震动激励下较单维地震动激励下结构响应大，因此，大跨度斜拉桥抗震研究应充分考虑地震动的多维性与行波效应的影响。

关键词：大跨度斜拉桥；随机响应；行波效应；多维输入；功率谱密度

大跨度斜拉桥得益于设计理论完善、新材料与新工艺的开发、施工技术的创新，跨度、承载能力和净空等方面有了更大的提升。桥梁作为一项生命线工程，发生较大地震时，局部薄弱结构易发生破坏甚至整体倒塌，短时间内修复难度极大，交通陷于瘫痪，严重影响了灾后的救援工作，灾区人民的生命和财产可能发生巨大的损失。为降低地震灾害及次生灾害损失，根本性在于提高桥梁结构安全可靠性，而可靠性源于合理的抗震设计方法。

地震动空间变化客观存在[1，2]，国内外桥梁学者及工程界一致认为[3-6]，对大跨度结构的地震响应有重大影响。随机振动分析方法[7，8]也称为功率谱法，它是建立在地面运动统计性基础上，将具有统计性激励作用于结构，计算响应的均值，且随机振动方法输入是功率谱，从能量的角度来分析问题。因此，进行随机振动分析是更具有普遍性和统计性。

本文从非一致地震动输入的基本理论出发，采用随机振动方法，对某大跨度斜拉桥进行随机地震响应分析，分析单维及多维地震动激励下考虑地震动的行波效应对主梁及主塔的响应规律，并将单维及多维的计算结果进行了对比，为大跨度及超大跨度斜拉桥提供参考价值。

1多点地震动场输入的基本方程

对于离散线性结构系统，多个地面支撑与自由度，需要考虑将平动方向的地震动进行分解，其多点地震激励运动基本方程可写为如下简单形式[9]

(1)

(2)

由式(2)可得

(3)

忽略阻尼力，将式(3)和式(1)联合求解，可得

(4)

当集中质量矩阵，Msb=0，式(4)简化为

(5)

式(5)为多点地震动激励下输入的基本运动方程。

2多点随机地震动场的模拟及多维扩展

通过对强震记录数据的提取与分析，地震动是呈现空间变化特性，发生概率也是随机的，已有不少学者对多点随机地震动模型进行了研究，包括互功率谱密度函数与自功率谱密度函数[10]，考虑多维地震动分量，地面各点加速度互功率谱密度函数表示为

(6)

式(6)中，Smm(iω)表示支承处自功率谱密度函数，表征局部场地效应；Skl(iω)表示支承处互功率谱密度函数，用来描述地震动空间变化特性

(7)

式(7)中，ρkl(iω)为相干函数，可表示为

(8)

式(6)为单维多点功率谱密度函数，则多维多点功率谱密度函数可将式(6)中各点均按下式进行三维扩展

(9)

本文采用较成熟的加速度功率谱模型Clough和Penzien模型[12]，即

(10)

式(10)中，ωg，ξg为土层的特征频率和阻尼比，ωf，ξf为低通滤波器频率和阻尼比参数，其目的是为控制模型中低频成分，该功率谱密度函数模型不仅适用于低频结构、中高频结构的随机地震响应分析，适用范围更广。选取支承处同为硬场地进行分析，参数的取值如表1所示。

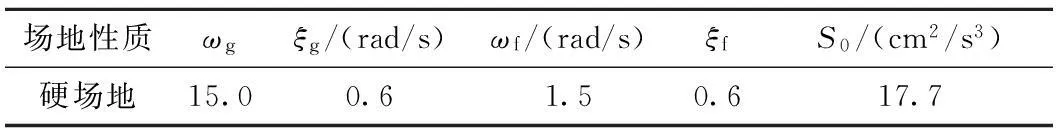
表1　Clough和Penzien模型相关参数取值

3数据仿真分析

3.1有限元计算模型

采用的结构模型为某大跨度斜拉桥，该公路桥总长为1280 m，跨径对称分布，中间跨度为680 m，主梁截面形式采用流线形扁平钢箱梁，宽度28.7 m，高度3.5 m，设2.0%双向坡，采用半漂浮体系。双索面，每面由21×2根索组成，采用扇形布置，索塔的结构为花瓶形式，C50混凝土，自承台顶以上塔高223.0 m，主塔由两塔柱及3道横梁组成，各构件均采用单箱单室截面，下横梁为等高梁，梁高7.0 m，宽10.0 m，中横梁梁高5.0 m，宽8.0 m，上横梁梁高3.0 m，宽6 m。采用有限元方法对该桥进行离散模拟，利用ANSYS中的beam44梁单元来模拟主塔结构，link8杆单元来模拟斜拉索，共6种截面形式，截面积范围0.004 899～0.009 980 m2，通过输入常数初始应变考虑斜拉索初应力，采用多段直杆法即多个杆单元节点来模拟斜拉索中间段的运动，从而模拟斜拉索的非线性性质，beam4梁单元来模拟钢箱梁和辅助墩。未考虑桩土共同作用，计算模型见图1，忽略二期恒载质量作用，纵桥向用X表示，竖桥向用Y表示，横桥向用Z表示。

图1　三维有限元计算模型

3.2动力特性分析

采用兰索斯块形划分法对大跨度斜拉桥进行了模态分析，前5阶的动力特性如表3所示。

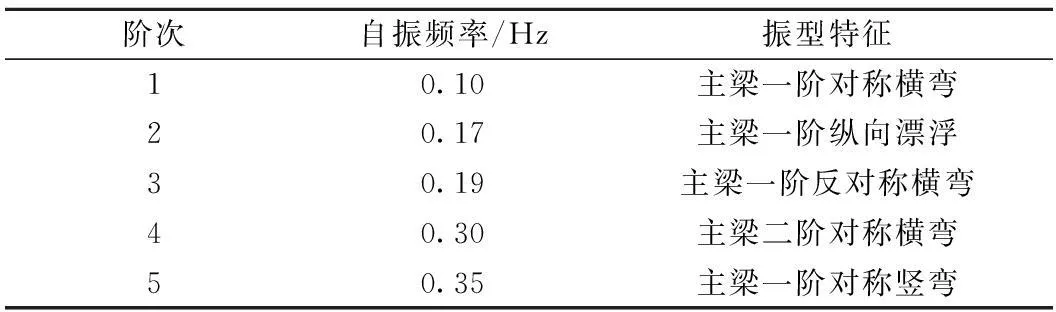
表2　大桥的动力特性

3.3行波效应对结构响应的影响

为研究大跨度斜拉桥在地震动行波效应下的响应规律，借助通用软件ANSYS，后处理分析中，先输入功率谱密度函数曲线，通过对谱值曲线中视波速参数值的改变来考虑行波效应的影响，并将其施加于基础分别进行单维和三维功率谱激励，本文假定地震波沿纵桥向自#1塔柱底部支承处至#2塔柱底部支承处传播，采用常量vapp视波速，对应计算工况如表2所示。

表3　行波效应下计算工况

注：考虑地震动的行波效应时，假定#1塔和#2塔柱底部支承处的场地类别同为硬场地。

3.3.1单维地震作用下主塔与主梁的响应分析

图2、图3响应曲线为在纵向地震动激励时，主塔纵向弯矩与主梁纵向位移在考虑地震动的行波效应下的响应规律。考虑地震动的行波效应后，位移和内力响应较一致激励有所降低，主塔的纵向弯矩响应曲线沿塔高平缓，#1塔、#2塔柱底部的纵向弯矩分别从101.9 MN·m降至67.1、98.0 MN·m降至63.3 MN·m；主梁纵向位移在全跨度范围内的响应值变化很小，呈一条直线，从一致激励工况A的45.3 mm降至工况D的25.1 mm，降幅较大。

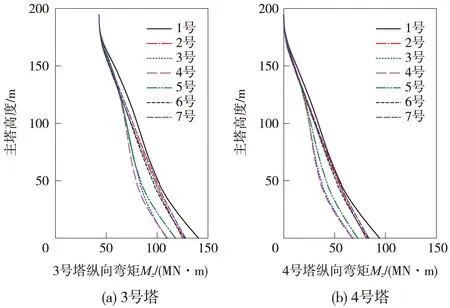
图2　两塔纵向弯矩

图3　主梁纵向位移

图4、图5响应曲线为在横向地震动激励时，主塔竖向弯矩与主梁横向位移在考虑地震动的行波效应下的响应规律。考虑地震动的行波效应对除#2塔竖向弯矩响应影响很小外，对#1塔竖向弯矩与主梁的横向位移响应影响较大。具体地，主塔的竖向弯矩响应的峰值出现在横梁部位，#1塔柱底部的竖向弯矩从一致激励工况A的216.6 MN·m降至工况E的190.9 MN·m；主梁的横向位移响应较大值出现在梁端部和跨中部，跨中的响应值从一致激励工况A的68.6 mm降至工况E的48.9 mm，降幅较大。

图4　两塔竖向弯矩

图5　主梁横向位移

3.3.2多维地震作用下主塔与主梁的响应分析

图6～图9响应曲线为在多维地震动激励时，主塔纵向弯矩、竖向弯矩与主梁纵向位移、横向位移在考虑地震动的行波效应下的响应规律。总体来看，多维地震动计算结果为地震动分量联合作用，结构响应在多维地震动作用下较单维地震动作用下明显增大，不同工况下对结构的响应程度是不一样的。表4列出了在多维与单维地震动作用下同时考虑地震动的行波效应主塔与主梁特殊部位的响应对比，可以得出，考虑地震动的行波效应时，除主梁跨中纵向弯矩外，结构响应均有所减小。

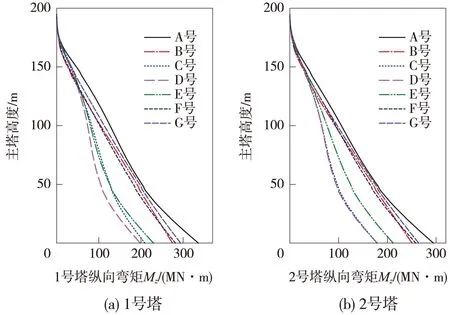
图6　两塔纵向弯矩

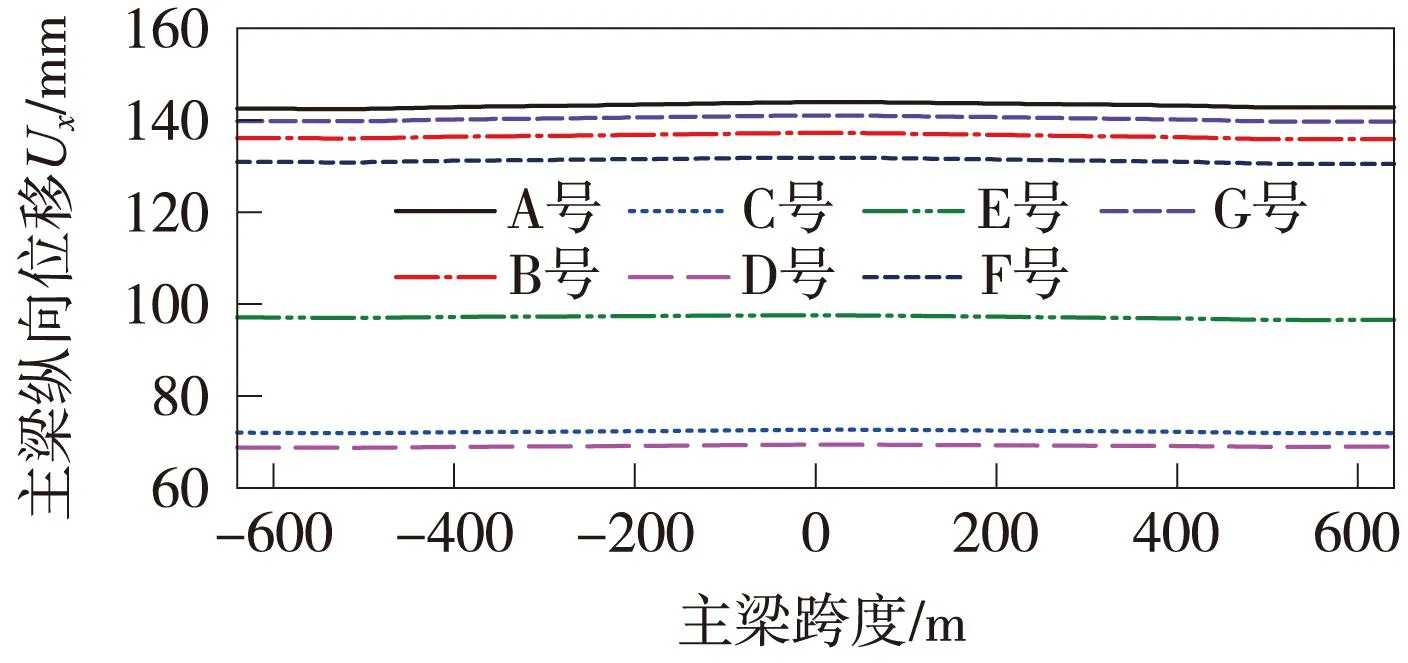
图7　主梁纵向位移

4结论

(1)地震动的行波效应是影响大跨度斜拉桥结构响应的重要因素。结构响应随着视波速的变大呈现振荡变化，最后趋近于一致激励。

(2)地震动的行波效应对大跨度斜拉桥响应的影响趋有所不同，随着视波速的增大，有减小的结构响应，也有增大的结构响应。与一致激励工况A相比，在工况D条件下，纵向激励时，主梁跨中纵向位移减小了44.5%；横向激励时，主梁跨中横向位移减小了30.3%；多维激励时，主梁跨中纵向位移和横向位移分别减小了51.8%和31.6%，而主梁跨中纵向弯矩在纵向激励及多维激励下分别增大了20%和3.9%。

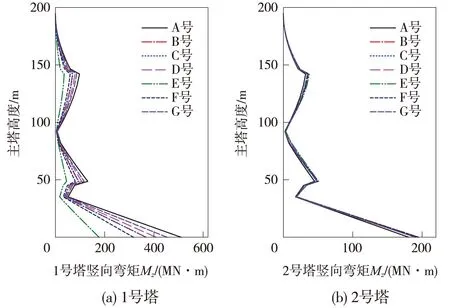
图8　两塔竖向弯矩

图9　主梁横向位移

(3)考虑地震动的行波效应时，不同的地震视波速对大跨度斜拉桥响应的影响程度不同，纵向激励时，视波速为300 m/s时位移和内力响应值最小，而横向激励时，视波速为500 m/s时位移和内力响应值最小。因此，分析结构响应需要充分考虑地震波的传播速度与传播方向。

(4)与单维纵向激励下结构响应对比，不论是否考虑地震动的行波效应的影响，大跨度斜拉桥在多维激励下结构响应成倍增大，#1塔和#2塔柱顶的纵向位移在不考虑地震动的行波效应下分别增大了2.3倍和2.1倍，在考虑地震动的行波效应下分别增大了2.0倍和1.8倍。所以，大跨度斜拉桥进行结构抗震设计时，必须充分考虑地震动的多维性与行波效应的影响。

表4　数据对比分析

注：选择计算工况D作为考虑地震动的行波效应下的响应值来进行比较

参考文献：

[1]Kiureghian A D， Neuenhofer A. Response Spectrum Method for Multi-Support Seismic Excitations[J]. Earthquake Engineering and Structural Dynamics， 1992，21(8):713-740.

[2]潘旦光，楼梦麟，范立础.多点输入下大跨度结构地震反应分析研究现状[J].同济大学学报，2001，29(10)：1213-1219.

[3]A. S. NazmyA.M. Abdel-Ghaffar. Effects of Ground Motion Spatial Variability on the Response of the Cable-stayed Bridges[J]. Earthquake Eng. Struct. Dyn. 1992，21(1):1-20.

[4]R. S. Harichandran， A. Hawwari and B. N. Sweidan. Response of Long-span Bridges to Spatially Varying Ground Motion[J]. Struct. Eng, 1996，122(5):476-484.

[5]苗家武，胡世德，范立础.大型桥梁多点激励效应的研究现状与发展[J].同济大学学报，1999，27(2)：189-193.

[6]钟万勰，林家浩，吴志刚，等.大跨度桥梁分析方法的一些进展[J].大连理工大学学报，2000，40(2)：127-135.

[7]Perotti F. Structural Response to Non-Stationary Multi-Support Random Excitation[J]. Earthquake Engineering and Structural Dynamics， 1990，19:513-527.

[8]Harichandran R.S. An Efficient Adaptive Algorithm for Large Scale Random Vibration Analysis[J]. Earthquake Engineering and Structural Dynamics，1993，22:151-165.

[9]Clough R W and Penzien J. Dynamics of Structures. McGraw-Hill， Inc.， 1975.

[10]胡聿贤.地震工程学[M].北京：地震出版社，1988.

[11]Olivera C S， Hao H， Penzien J. Ground Motion Modeling for Multiple-input Structural Analysis[J]. Structural Safety， 1991，10:79-93.

[12]Clough R W， Penzien J. Dynamics of Structures[M]. New York: McGram-Hill，Inc.，1993.

Analysis of Stochastic Seismic Response to Traveling Wave Effect on Long-span Cable-stayed Bridge

LUO Ze-hui

(China Railway Eryuan Engineering Group Co.， Ltd.， Chengdu 610031， China)

Abstract：Because of the large distance between supports of the long-span cable-stayed bridge (LSCSB) and the limited propagation speed of the seismic wave， there exists some time difference when the seismic wave reaches the supports. As a result， the analysis method of uniform excitation cannot meet the actual situation. Thus， a long-span cable-strayed bridge with 680 m main span is taken for calculation and a finite element model is established to analyze the seismic response of the main girder and the towers with traveling wave effects under one-dimensional and multi-dimensional random seismic excitations. And a comparative analysis between uniform earthquake excitations and non-uniform earthquake excitations is conducted. The results show that compared to uniform excitations， longitudinal displacements of the middle span decrease 42.3% and 44.8% and the vertical bottom moments of No.1 tower and No.2 tower decrease 25.9%， 19.9%， and 0.4%， 1.2% respectively under longitudinal earthquake excitations when wave velocity is 200 m/s and 300 m/s. Structural response under multi-dimensional earthquake excitations is larger than that under one-dimensional earthquake excitations. Therefore， effects of dimensionality of earthquake motions and traveling wave should be fully considered in the seismic analysis for LSCSB.

Key words：Long-span cable-stayed bridge; Stochastic response; Traveling wave effect; Multi-dimensional excitation; Power spectral density

中图分类号：U448.27

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2015.06.020

文章编号：1004-2954(2015)06-0088-05

作者简介：罗泽辉(1982—)，男，工程师，2009年毕业于西南交通大学，

收稿日期：2014-10-29； 修回日期：2014-11-05