梯形轨道-普通整体道床过渡段布置方式研究
江万红,任娟娟,解 鹏,刘 欢,欧阳明
(1.中铁二院工程集团有限责任公司,成都 610031;
2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031;
3.广州铁路(集团)公司广州大型养路机械运用检修段,广州 511487)
梯形轨道-普通整体道床过渡段布置方式研究
江万红1,任娟娟2,解鹏2,刘欢2,欧阳明3
(1.中铁二院工程集团有限责任公司,成都610031;
2.西南交通大学高速铁路线路工程教育部重点实验室,成都610031;
3.广州铁路(集团)公司广州大型养路机械运用检修段,广州511487)
摘要:梯形轨道与普通整体道床的过渡部分,由于两种轨道结构形式的轨下基础刚度存在差异,从而影响行车平稳性和钢轨使用寿命。采用线性增加梯形轨道纵向轨枕下减振胶垫个数,作为梯形轨道-普通整体道床过渡段设置方式,建立车辆与过渡段轨道耦合动力学模型,分析不同过渡段设置方式钢轨垂向位移和车体垂向加速度的变化。计算表明,在两种轨道形式连接处梯形轨道的纵向轨枕下,采9个减振胶垫,以等间距0.625 m布置的过渡段设置方式较为合理。
关键词:梯形轨道;过渡段;轨道刚度;动力计算
梯形轨道由钢轨、梯形轨枕、支承块构成,具有减振降噪、少维修等特点[1-2],近年来在我国北京、上海等地的地铁中有所应用[3]。对于梯形轨道与普通整体道床的过渡部分,在列车驶经两种轨道结构连接处时,由于轨下基础刚度相差较大,钢轨垂向位移和车体垂向加速度将发生急剧变化,严重影响行车的平稳性和钢轨的使用寿命,因此须在两种轨道间设置过渡段[4-5]。为此,采用车辆-轨道耦合动力学分析方法,对梯形轨道-普通整体道床合理过渡段设置方式进行研究。
1梯形轨道-普通整体道床过渡段布置方式
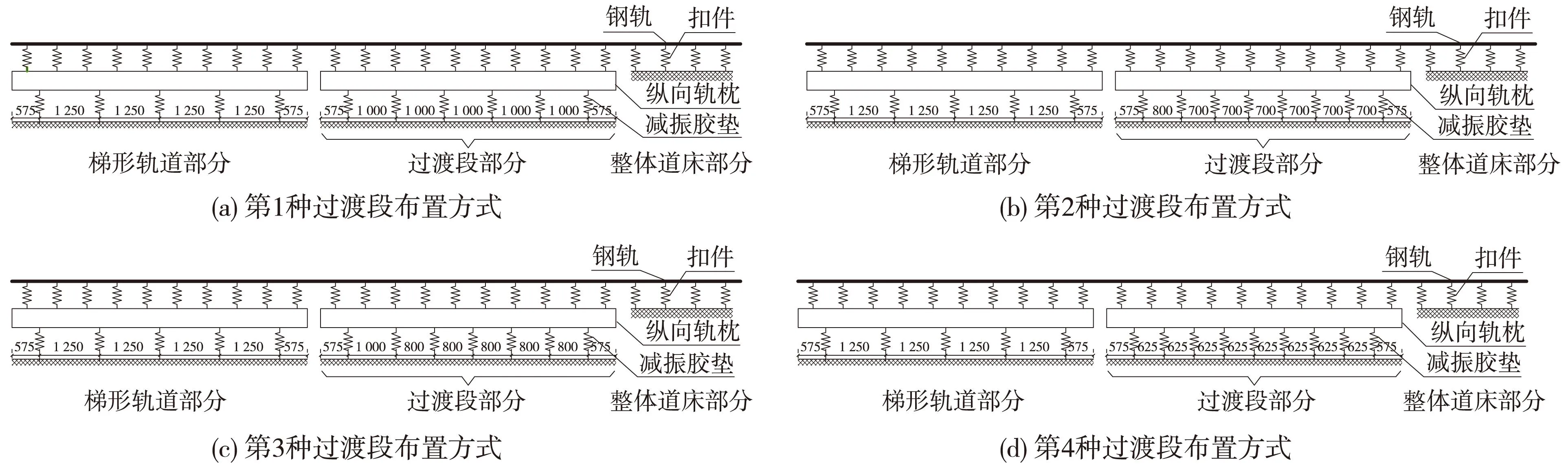
图1 梯形轨道-普通整体道床过渡段不同设置方式(单位:mm)
参考贵阳城市轨道交通1号线相关设计研究资料,梯形轨道-普通整体道床过渡段布置方式共分4种,采用线性改变2种轨道连接处一块纵向轨枕下减振胶垫数量,改变减振胶垫间距,以调整梯形轨道刚度,从而实现梯形轨道与普通整体道床的合理过渡。第一种过渡段布置方式,过渡段部分采用6个减振胶垫等间距布置(1.0 m);第二种过渡段布置方式,过渡段部分采用7个减振胶垫,第一和第二个减振胶垫间距为1.0 m,其余减振胶垫采用等间距布置(0.8 m);第三种过渡段布置方式,过渡段部分采用8个减振胶垫,第一和第二个减振胶垫间距为0.8 m,其余减振胶垫采用等间距布置(0.7 m);第四种过渡段布置方式,过渡段部分采用9个减振胶垫等间距布置(0.625 m)。不同的过渡段布置方式如图1所示。
2模型及计算参数
2.1车辆与过渡段轨道耦合动力学模型
本文运用大型通用有限元软件Ansys进行计算,模型总长度取100 m,其中梯形轨道长度取50 m,整体道床轨道长度取50 m。当车辆走行经过过渡段部分时,计算研究钢轨和车体垂向的变化。考虑到与扣件弹性相比,将普通整体道床简化为刚性基础是合理的,故过渡段模型不考虑基底刚度影响,将其视为固端约束[6]。
其中,钢轨采用3D梁单元模拟,纵向轨枕采用2D平面板单元模拟,扣件、减振垫层和缓冲垫层采用非线性弹簧单元模拟;车辆采用地铁B型车,以一节列车作为研究对象,简化为具有一、二系悬挂的由车体、构架及轮对组成的多刚体系统;出于安全余量等因素考虑,行车速度设计为160 km/h。动力学模型[7-8]见图2。

图2 车辆与过渡段轨道耦合动力学模型示意
2.2有限元模型计算参数
梯形轨道-普通整体道床过渡段轨道结构的主要参数见表1。
地铁B型车的计算参数见表2。

表1 梯形轨道-整体道床过渡段轨道结构主要参数

表2 地铁B型车基本参数
3梯形轨道-普通整体道床过渡段动力学计算
通过模拟车辆在钢轨上的走行,研究过渡段部分垂向响应[9-10]。运用大型通用有限元计算软件Ansys,考虑到边界条件的影响,故模型两边各预留12.5 m不作为研究范围,所成图形中,横坐标原点表示不同轨道结构交界处,横坐标负半轴表示梯形轨道部分距离坐标原点的距离,横坐标正半轴表示普通整体道床部分距离坐标原点的距离。
3.1相同过渡长度情况下的不同过渡段布置方式对比分析
(1)钢轨垂向位移及位移变化率
以2种轨道结构形式连接处一个纵向轨枕长度作为过渡部分,划分5种工况计算,即:不设置过渡段、第一种过渡方式、第二种过渡方式、第三种过渡方式和第四种过渡方式。钢轨垂向位移曲线和钢轨垂向位移变化率曲线如图3、图4所示。

图3 钢轨垂向位移曲线
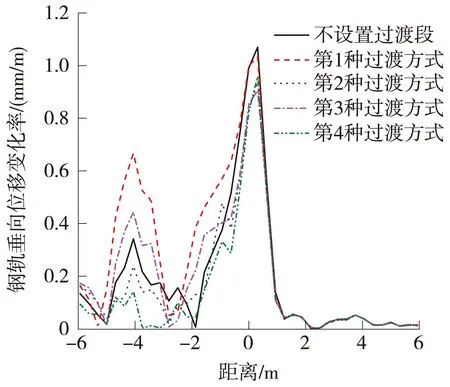
图4 钢轨垂向位移变化率
从图3中可得,当过渡长度相同时,不同的过渡段设置方式对钢轨的最大垂向位移值影响较大。不设置过渡段钢轨最大垂向位移为2.119 mm,第一种过渡方式比不设置过渡段的最大钢轨垂向位移值增加0.433 mm;第三种过渡方式和不设置过渡段的最大钢轨垂向位移值相差不大;第二种过渡方式比不设置过渡段的最大钢轨垂向位移值减小0.2 mm,减小幅度10%左右;第四种过渡方式比不设置过渡段的最大钢轨垂向位移值减小0.31 mm,减小幅度15%左右。
由图4可知,当车辆由梯形轨枕轨道一侧驶入过渡段时,由于轨道刚度的改变,引起钢轨垂向位移变化率值的增加,但增加幅度不大;当车辆由过渡段部分驶入整体道床一侧时,钢轨垂向位移变化率因轨道刚度剧烈改变而明显增加。在梯形轨道与普通整体道床过渡的临界位置,钢轨垂向位移变化率值达到最大。不设置过渡段最大钢轨垂向位移变化率为1.07 mm/m,设置过渡段以后,最大钢轨垂向位移变化率值比不设置过渡段时有所减小,其中第二种、第三种和第四种设置方式最大钢轨垂向位移变化率值相差不大,相应的最大钢轨垂向位移值分别为0.94、0.90 mm/m和0.95 mm/m。综上所述,相同过渡长度下第四种过渡段设置方式的钢轨垂向位移值和钢轨垂向位移变化率值最小。
(2)车体垂向加速度
评价车辆的舒适性最直接的标准就是车体振动加速度,我国车体垂向振动加速度的舒适度标准可取为0.13g[11]。车辆走行时,相同过渡长度不同过渡段布置方式所引起的车体垂向振动加速度随时间变化曲线如图5所示。

图5 车体垂向加速度曲线
由此可得,不布置过渡段、第一种过渡布置方式和第三种布置过渡方式车体最大垂向加速度值相对较大,其数值分别为0.152、0.199 m/s2和0.143 m/s2;第二种过渡布置方式和第四种过渡布置方式车体最大垂向加速度值相对较小且相差不大,对应数值为0.102 m/s2和0.090 m/s2。可以看出,第四种过渡布置方式的车体最大垂向加速度值为最优,对比不设置过渡段车体最大垂向加速度值减小0.062 m/s2,减小幅度约为41%。
(3)轮轨力及减载率
我国《铁道车辆动力学性能评定和试验鉴定规范》(GB 5599—85)规定车辆的轮重减载率应符合以下条件:≤0.65(第一限度,合格标准),≤0.6(第二限度,增大安全余量的标准)[12]。按照增大安全余量的标准,本文取第二限度。经计算5种工况下的最大轮重减载率均符合规范要求,具体数值见表3。

表3 不同过渡设置方式的最小轮轨力和最大轮重减载率
3.2相同过渡段布置方式情况下的不同过渡长度对比分析

图6 钢轨垂向位移

图8 车体垂向加速度
以第四种过渡段设置方式作为研究对象,针对不同的过渡段长度进行有限元结构动力学计算分析。分别取1个梯形轨枕、2个梯形轨枕和3个梯形轨枕长度作为梯形轨道和整体道床的过渡部分,计算得出钢轨垂向位移值、钢轨垂向位移变化率值和车体垂向加速度值的变化情况,如图6~图8所示。计算表明,分别以1个梯形轨枕、2个梯形轨枕和3个梯形轨枕长度作为梯形轨道与整体道床的过渡部分,相应的钢轨最大垂向位移值为1.806、1.806 mm和1.807 mm,钢轨最大垂向位移值变化不大;相应的钢轨最大垂向位移变化率分别为0.959、0.954 mm/m和0.950 mm/m,钢轨最大垂向位移变化率值改变不明显;相应的车体最大垂向加速度分别为0.090 5、0.089 1 m/s2和0.095 2 m/s2,车体最大垂向加速度值变化幅度很小。综上所述,过渡段长度的改变对钢轨垂向位移值、钢轨垂向位移变化率值和车体垂向加速度值无明显影响。从施工方便和经济节约方面考虑,结合贵阳城市轨道交通1号线实际设计资料,取1个梯形轨枕长度作为梯形轨道-普通整体道床的过渡部分较为合适。
4结论
(1)普通整体道床与梯形轨道的轨下基础刚度差异较大,应当设置过渡段,设置过渡段可以改善轨道结构各项指标。
(2)当过渡段长度相同时,对比不同过渡段布置方式的钢轨垂向位移图、钢轨垂向位移变化率图和车体垂向加速度图可得。考虑到施工便利性,第四种过渡方式是较为合理的梯形轨道与普通整体道床过渡形式。
(3)以第四种过渡方式为例,过渡段长度变化对钢轨最大垂向位移值、钢轨最大垂向位移变化率值和车体最大垂向加速度值影响很小。所以,从经济性角度考虑,当采用同种过渡段设置方式时,梯形轨道-普通整体道床过渡段长度取1个梯形轨枕范围即可。
参考文献:
[1]周宇,许玉德,李海峰.梯子式轨道结构系统[J].城市轨道交通研究,2002(1):21-23.
[2]苏宇,刘维宁,孙晓静,等.梯形轨道减振性能研究[J].铁道标准设计,2007(10):71-74.
[3]张珍珍.梯形轨枕轨道力学性能分析[J].铁道勘测与设计,2010(6):34-37.
[4]孔祥仲,刘伟平,王其昌,等.板式轨道过渡段刚度设计计算方法[J].铁道标准设计,2000(9):7-9.
[5]蔡成标,刘增杰,赵汝康.浮置板轨道过渡段的动力学设计[J].铁道建筑,2003(12):41-44.
[6]于建平.钢弹簧浮置板轨道过渡段动力性能分析与设计[D].成都:西南交通大学,2013:15-16.
[7]杨新文,和振兴.梯形轨枕轨道振动特性研究[J].振动工程学报,2012(4):389-393.
[8]寸东东,曾京,齐琳.纵向轨枕轨道振动特性数值分析[J].铁道标准设计,2012(8):8-12.
[9]李朝锋.高速客运专线铁路铺设无砟轨道过渡段结构设计[J].铁道标准设计,2009(7):1-4.
[10]陈伯靖,周建,李成辉.浮置式梯形轨枕轨道减振器刚度对轨道动力特性影响分析[J].铁道标准设计,2013(1):5-7.
[11]翟婉明.车辆-轨道耦合动力学[M].北京:中国铁道出版社,2001.
[12]国家标准局.GB5599—1985铁道车辆动力学性能评定和试验鉴定规范[S].北京:中国标准出版社,1986.
Study on Setting-up of Transition Section between Ladder Track and Monolithic roadbedJIANG Wan-hong1, REN Juan-juan2, XIE Peng2, LIU Huan2, OU Yang-ming3
(1.China Railway Eyuan Group Co., Ltd., Chengdu 610031; 2.MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031; 3.Heavy Machinery Road Maintenance Division, Guangzhou Railway Group Corporation, Guangzhou 511487)
Abstract:Owing to the stiffness differences of foundations under ladder track and monolithic roadbed, the train running smoothness and service life of rail are deeply affected. The paper establishes the coupling dynamics model of“vehicle-rail”, sets up the transition section by linear increase of the number of the damping rubber pad under the ladder track, and investigates the change pattern of the vertical displacement of rail and acceleration of vehicle in different settings of transition section. The result shows that it is more reasonable to install nine damping rubber pads with equal spacing of 0.625m under longitudinal sleepers of ladder track at the joint of the two track structures.
Key words:Ladder track; Transition section; Track stiffness; Dynamic calculation
中图分类号:U213.2+41
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2015.05.016
文章编号:1004-2954(2015)05-0074-04
作者简介:江万红(1982—),男,工程师,工学硕士,E-mail:214035258@qq.com。
收稿日期:2014-08-22; 修回日期:2014-08-30

