基于Three Factor+C模型改进的地形辐射校正方法

张伟阁， 杨辽， 曹良中， 贾洋

(1.中国科学院新疆生态与地理研究所荒漠与绿洲生态国家重点实验室，乌鲁木齐 830011；2.中国科学院大学，北京 100049)

基于Three Factor+C模型改进的地形辐射校正方法

张伟阁1,2， 杨辽1， 曹良中1,2， 贾洋1,2

(1.中国科学院新疆生态与地理研究所荒漠与绿洲生态国家重点实验室，乌鲁木齐 830011；2.中国科学院大学，北京 100049)

地形辐射校正(简称“地形校正”)是复杂地形遥感定量化研究的关键环节之一。针对传统的经验地形校正模型存在的不同坡度采用同一校正系数的缺陷，基于简化的Three Factor+C模型，借鉴改进型Minnaert模型中坡度分级的思想，提出了基于Three Factor+C+坡度的地形校正方法。结果表明，使用Three Factor+C+坡度模型进行地形校正后的遥感图像，其均值、标准差、像元值与光照系数的相关性、阴阳坡光谱辐亮度值、离散指数和同质系数等6个指标均优于参与比较的C模型、SCS模型、Three Factor模型和Three Factor+C模型的对应指标。Three Factor +C+坡度模型有比较完善的物理机制，并较好地消除地形对光谱辐亮度的影响，值得推广。

地形校正；Three Factor +C模型；坡度分级；离散系数；同质系数

0 引言

传感器、大气和地形是影响遥感数据质量的3大因素，为了消除其影响，需分别进行辐射定标、大气校正和地形辐射校正(以下简称“地形校正”)。地形校正作为辐射校正的最后一个环节，其目的就是消除或减缓地形因素对地物真实光谱值的影响。

30多a来，国内外学者先后建立并发展了一系列的地形校正模型。常用的模型包括经验模型(变经验系数法[1]和Civco模型[2])、物理模型(余弦模型[3]、SCS模型[4]和Three Factor模型[5])、半经验模型(Minnaert模型[6,7]、C模型[3]、SCS+C模型[8]和Three Factor +C模型[5])等。然而到目前为止，山区(特别是复杂山区)的地形影响仍然是中、高分辨率遥感数据定量化应用与研究的主要制约因素。基于朗伯体假设和太阳-地表-传感器三者之间的几何关系而构建的余弦校正模型，因其忽视了散射辐射和邻近辐射的影响而存在过度校正问题；C校正模型将C经验参数引入到余弦模型中，用于调节余弦模型的过度校正现象，在小尺度区域取得较为理想的结果，但在整体上仍存在过度校正问题；Minnaert模型将Minnaert函数引入余弦模型中，已考虑地表的非朗伯体特性，在落叶林和混交林山区效果较好，但在针叶林山区却不尽人意[9]。基于太阳-冠层-传感器三者几何关系而构建的SCS模型改进了向阳坡面的校正精度，但在背光区域仍存在过度校正问题；Soenen等[9]将SCS模型和C模型结合，建立了SCS+C模型，大大提升了地形校正精度。Zhang等[5]考虑太阳直接辐射、天空散射辐射和邻近地表辐射的影响建立了具有完善机理的物理校正模型(Three Factor模型)，并引入C经验系数对其进行了改进，建立了Three Factor +C模型；针对Three Factor +C模型复杂的计算，高永年等[10]对其进行了简化，使得该模型计算简单、易操作。

尽管引入各种参数的校正模型已经得到广泛应用，但是针对不同坡度像元采用同一个校正系数，无法反映同一太阳方位角下不同坡度的[9]差异。为此，陆灯盛等[11]提出的改进型Minnaert模型对图像样本进行了坡度分级，并用拟合的各波段不同坡度下的Minnaert系数取代单一的校正系数，该方法既有效去除了遥感图像的地形效应，又保持了图像的纹理和光谱特性，是山区图像地形校正的有效方法之一。本文引入该方法，并将其与Three Factor+C模型相结合，提出Three Factor+C+坡度的校正方法，旨在进一步提高该模型的校正精度。

1 模型与方法

1.1 Three Factor模型

Three Factor模型(本文简称TF模型)是一种纯物理机制的地形校正模型，它比较全面地考虑了太阳直射、天空散射和邻近地表对像元光谱辐射值的影响，该模型可表示为

(1)

式中：LH为校正后像元的辐亮度；LT为校正前像元的辐亮度；θ为太阳天顶角；i为太阳入射角；cosi为光照系数；r为水平地表接收到的天空散射辐射与天文太阳辐照度的比值；Vt为地形观测因子；Vd为天空观测因子；ø为遮蔽因子，当cosi>0时，ø=1，否则ø=0；T(λ,θ)为直射光下行辐射透过率；ρmean为邻近地表平均发射率。其中，cosi可表达为

cosi=cosθcose+sinθsinecos(φm-φs) ,

(2)

式中：e为坡度；φm为太阳方位角；φs为坡向。

1.2 Three Factor +C模型

参照高永年等[10]对Three Factor +C模型(本文简称“TF+C模型”)的简化，该模型可以表示为

(3)

式中:C为引入“TF+C校正模型”的经验系数，并且C=a/b;a，b系数可通过式(4)进行线性回归求得，即

LT=a+bcosi

(4)

1.3 模型改进思路

地形复杂区域的坡度往往变化很大，即使属于同一类地物的像元，所对应的太阳入射角和天空散射辐射也会因坡度变化而不同，其像元光谱辐亮度值也会有明显差异。因此，针对不同的坡度，ThreeFactor+C模型的系数C(经验系数)具有其对应的值。基于这种思路，本文针对Three Factor+C模型中系数C的取值，采用坡度分级的方法(本文简称“TF+C+坡度模型”)，使其在不同的坡度具有不同的C值，以提高地形校正的精度。

1.4 模型评价方法

1.4.1 传统方法

用于地形校正精度评价的传统方法主要有地形校正前、后图像的目视比较，均值比较，标准差比较和像元光谱辐亮度与光照系数(cosi)的相关程度比较。其中，目视比较法是最简单和最直接的地形校正效果评价方法，可以定性判断出地形校正是否合理；均值比较和标准差比较用于定量评价地形校正的结果，地形校正后图像的均值增加而标准差减少，则表明校正精度高。像元光谱辐亮度与cosi的相关程度也是评价地形校正效果的一个重要指标，其值越低，校正效果越好。

1.4.2 离散指数法

离散指数(discrete index，DI)可表达为

DI=(SD/M)×100%

(5)

式中：SD为标准差；M为均值。DI越小，表明地形校正效果越好。

1.4.3 同质系数法

同质系数(homogeneity coefficient，HOM)是一种基于纹理运算的校正评价方法，通过移动窗口计算窗口内像元值之间的同质性。由于地形校正减少了地形对像元值的影响，因此地形校正后窗口内各像元之间的光谱差异将减少，而同质系数将增加。同质系数可表达为

(6)

式中：HOM(i,j)为像元(i,j)的同质系数；n为移动窗口大小；vi,j为移动窗口内像元(i,j)的辐亮度值。则校正前、后整景图像的同质系数可表达为

(7)

式中：Ms为整景图像的同质系数；N为图像的像元个数。Ms越大，说明像元之间的异质性越小，校正效果越好。

2 校正实验

2.1 实验区与数据源

实验区位于天山北坡三工河流域的阜康市境内，海拔在1 400～4 000 m之间，平均高程为2 577 m。低山带[1 400～1 700 m)植被类型为半干旱草原，中山带[1 700～2 600 m)植被类型为云杉针叶林，亚高山带[2 600～3 500 m)植被类型为草甸，高山带[3 500 m以上)植被稀少，主要为冰雪和石砾。由于地形起伏巨大，地形效应很明显，并且区内主要被针叶林所覆盖，因而适合用于地形辐射校正研究。

研究采用的遥感数据为2010年8月13日获取的Landsat 5 TM数据，轨道号/行号为142/30，太阳天顶角为34.55°，方位角为138.53°。该数据来源于美国USGS网站(http: //glovis.usgs.gov/)，数据记录格式为GEOTIFF，产品级别为L1T。DEM数据由研究区1∶5万比例尺地形图数字化生成，像元精度为30 m(图1(左))。

图1 研究区DEM(左)，cosi(中)及TM4 系数C图像(右)

Fig.1 Images of DEM(left),cosi(middle) andCcoefficient of TM4(right)

2.2 数据处理步骤

1)辐射定标。采用光谱辐亮度计算公式[12]将TM图像的DN值转换为辐亮度值，并采用Chavez[13-14]的方法消除程辐射。将DEM与TM图像进行几何配准，配准精度控制在0.5个像元以内。计算cosi，得到cosi图像(图1(中))。将坡度分为10级，因45°以上的坡度较少，为确保样本数量，将45°以上的坡度分为一级，各级样本统计值见表1。

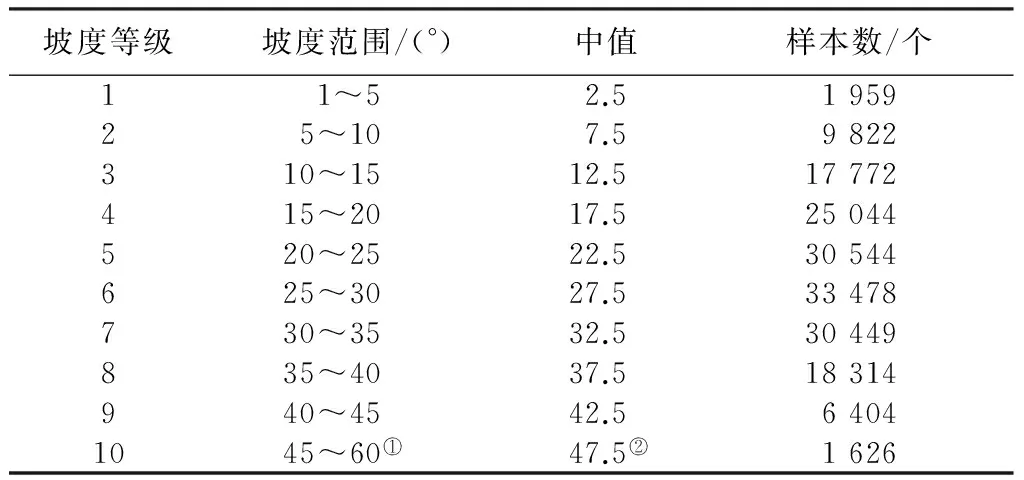
表1 各级坡度样本值统计Tab.1 Summary of selected samples from each slope group

①研究区内无坡度大于60°的像元；②坡度大于45°的像元样本数较少，故中值采用47.5。

2)坡度分级。用不同坡度级别对应的TM图像像元值，根据式(4)进行回归可获得10个对应坡度范围的系数C(图2)。

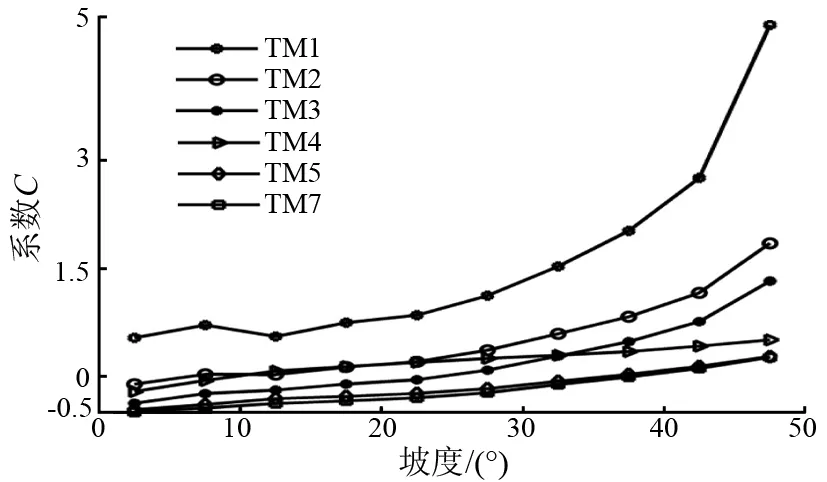
图2 系数C与各级坡度中值散点图Fig.2 Scatter plot of C coefficients and

利用不同坡度范围的系数C与10个坡度级别的中值进行模型拟合，并用决定系数R2和标准误差RMSE评判模型，最后发现五次多项式模型的R2已经大于0.99，完全符合要求(图3)。

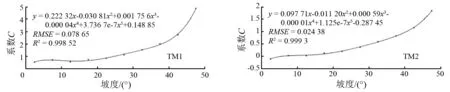
图3-1 各波段系数C与坡度的多项式回归模型拟合

Fig.3-1 Polynomial regression models simulating trend ofCvalues and slops for each band

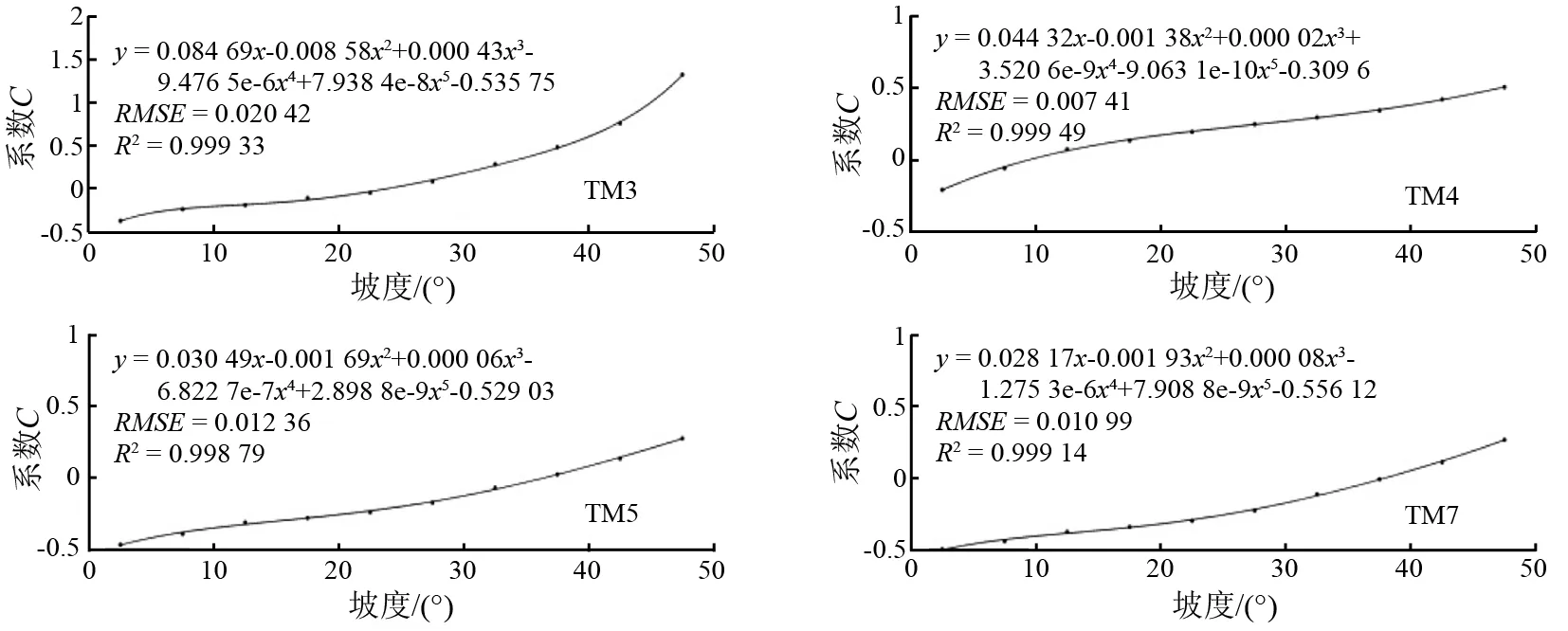
图3-2 各波段系数C与坡度的多项式回归模型拟合Fig.3-2 Polynomial regression models simulating trend of C values and slops for each band

3)系数C的计算。利用坡度图像和模拟得到的多项式方程，计算TM4图像各个像元的系数C，得到系数C图像(图1(右))。将系数C图像应用到式(3)中，进行Three Factor +C+坡度校正。校正过程中T(λ,θ)和ρmean参照高永年等[10]采用的方法进行取值。

3 校正结果评价

3.1 目视评价

本文引入C模型和SCS模型进行校正效果的目视比较，如图4所示。

(a) 原始图像 (b) C校正 (c) SCS校正

(d) TF校正 (e) TF+C校正 (f) TF+C+坡度校正

图4 原始图像及各模型校正后假彩色合成图像(TM5(R)4(G)3(B))效果比较

Fig.4 Comparison of false color composite images(TM5(R)4(G)3(B)) before and after

topographic correction with different models

从图4可以看出，各模型校正后图像的空间纹理信息量均有所提高，影像层次感增强，阴影区域变亮，光谱辐亮度得到了很大程度的改善。其中SCS校正和TF校正后图像中的阴影区域表现为亮度增强最为剧烈，存在过度校正现象；而C校正、TF+C较正和TF+C+坡度校正后图像中的阴影区域较为柔和，但无法从视觉上判断哪个效果更好；但TF+C+坡度模型校正后图像中的阴坡明显变亮，同种地物在阳坡和阴坡上的光谱值更加接近。

3.2 均值和标准差检验

均值和标准差的变化情况可以定量反映校正的效果，因此对原图像及各个模型校正后图像的子区域均值和标准差进行了统计(表2，表3)。

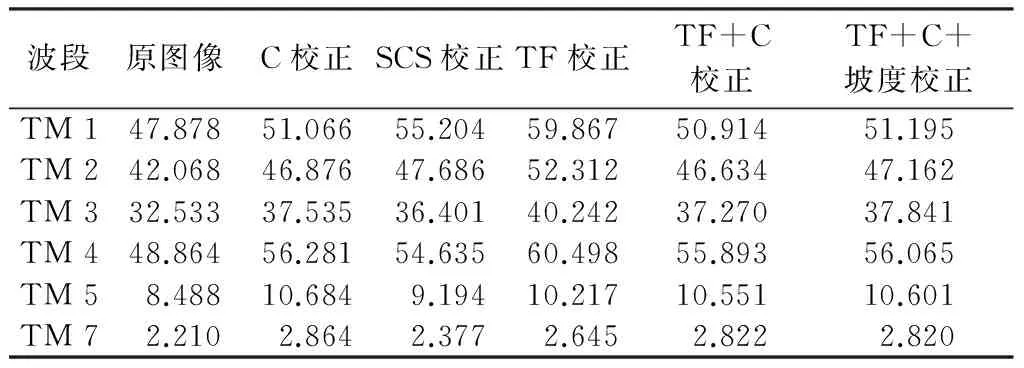
表2 地形辐射校正前后图像均值统计Tab.2 Statistics of mean values of images before and after topographic correction

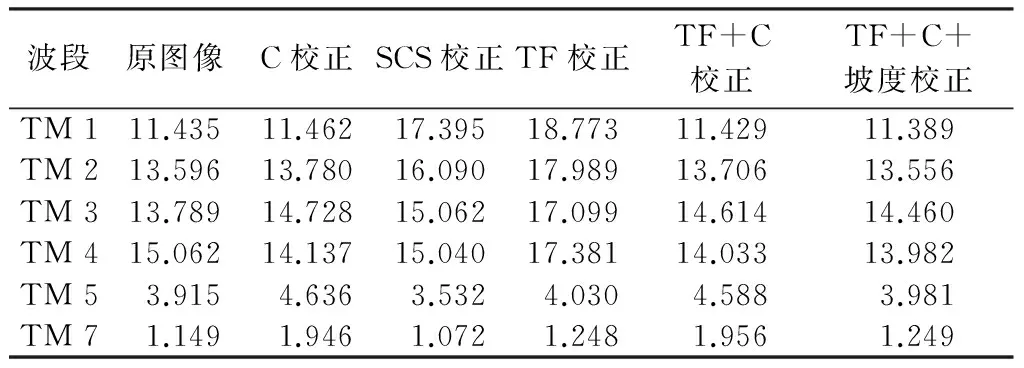
表3 地形辐射校正前后图像标准差统计Tab.3 Statistics of standard deviation values of images before and after topographic correction

从上述统计结果可以看出，各模型地形校正后图像的均值都有所增加，表明各校正模型都不同程度地削减了地形对阴影区域的影响；其中TF校正增加的最多，表明其校正过度。而从地形校正后图像的标准差来看，只有TF+C+坡度校正后图像的大部分波段的标准差比原始图像的标准差小，表明TF+C+坡度校正模型效果最好；C校正和TF+C校正前、后图像标准差变化不大，但TF+C校正后图像的大部分波段的标准差都比C校正的小，表明TF+C校正效果优于C校正；TF校正后图像的标准差最大，SCS校正后图像的次之，这2个模型校正后图像的大部分波段的标准差都比原始图像的大，表明TF校正和SCS校正精度并不理想。

3.3 光谱辐亮度与光照系数相关性检验

为了定量评价各模型的校正效果，本文对TM4原始图像及各模型校正后的图像进行了光谱辐亮度与光照系数(cosi)的相关分析(图5)。

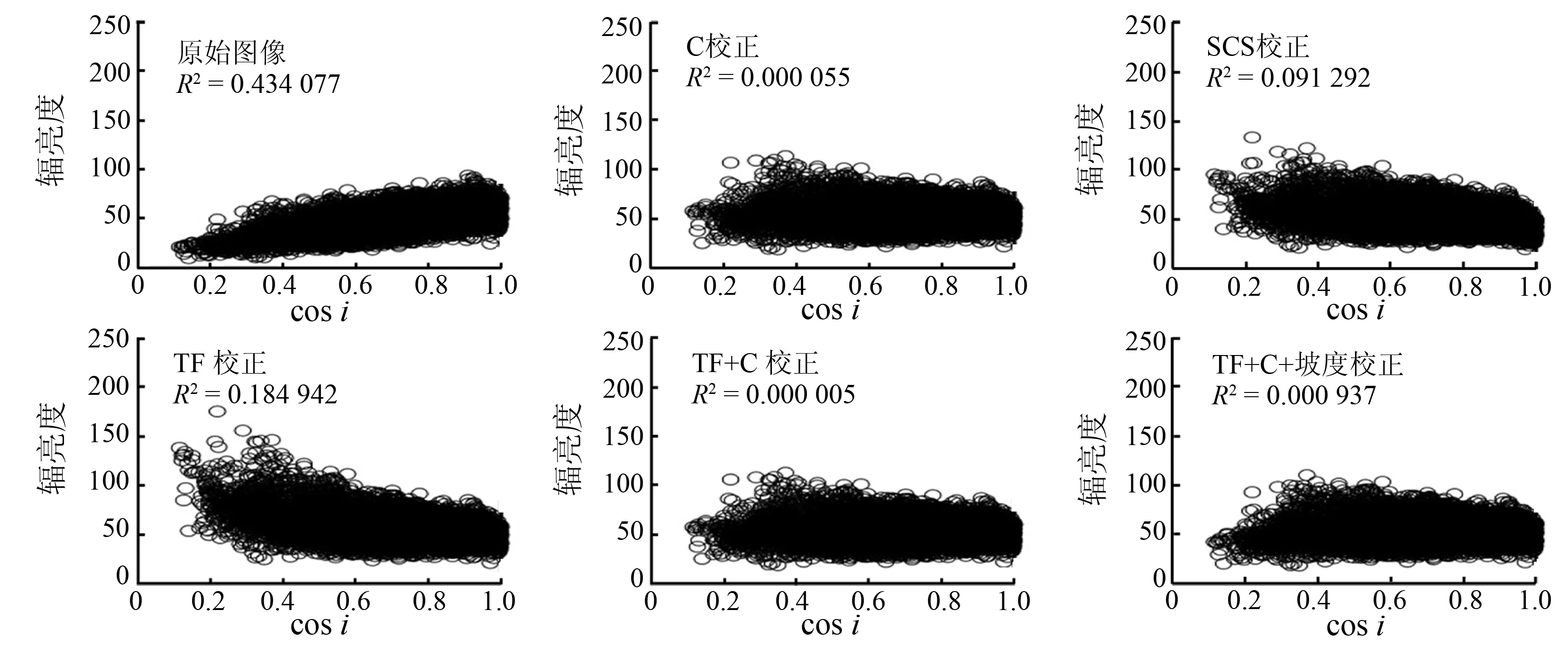
图5 TM4原始图像及各模型校正后图像光谱辐亮度与光照系数(cos i)相关性比较Fig. 5 Comparison of correlation between TM4 image radiance and cos i before and after topographic correction

从图5可以看出，原始图像的光谱辐亮度与光照系数(cosi)的相关性较高，R2=0.434；而各模型校正后TM4图像的光谱辐亮度与光照系数的相关性均降低，表明各模型都在不同程度上减弱了地形对图像的影响，其中C校正、TF+C校正和TF+C+坡度校正后的R2<0.001，说明图像的光谱辐亮度与光照系数的相关程度已经非常低，可见这3个模型的校正效果更优。

3.4 校正前后阴阳坡像元光谱曲线分析

本文分别随机选取10个位于阴坡和阳坡的同一森林地物类型点，取其光谱平均值，观察各校正模型校正前、后图像中阴坡和阳坡地物的光谱变化，其结果如图6所示。可以看出，由于地形的影响，同类地物在原始图像上阴坡的光谱辐亮度值要低于阳坡的，而经地形校正后，同类地物在阴坡和阳坡的辐亮度值趋于一致。图6所示结果表明，相比于其他模型，TF+C+坡度模型校正后图像中阴坡和阳坡的光谱曲线更加接近，并且TF+C+坡度模型校正后图像中阴坡光谱曲线与原始影像阳坡光谱曲线比较趋于一致。

图6 原始图像及各模型校正后图像中阴坡和

3.5 离散指数和同质系数检验

对各模型校正前、后的TM图像计算其各波段的离散指数(DI)，并基于5像元×5像元窗口计算的同质系数(Ms)进行对比(图7)。

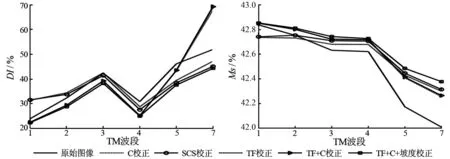
(a) 离散指数 (b) 同质系数

图7 原始图像及各模型校正后图像离散指数和同质系数比较

Fig.7 Comparison of dispersion indexes and homogeneity coefficients of images before and after topographic correction.

从图7(a)可以看出，各模型中只有TF+C+坡度模型校正后图像各波段的离散指数比原始图像的小，表明该模型校正效果最优。SCS模型在TM1和TM2图像的离散指数比原始图像的大，在TM3—TM5和TM7图像的离散指数比原始图像的小，表明该模型对原始图像TM3—TM5和TM7校正效果较好。TF模型在TM1—TM3图像的像元离散程度比原始图像的大，在TM4，TM5和TM7图像的像元离散程度比原始图像的小，表明该模型对TM4，TM5和TM7图像有较好的校正效果。C模型和TF+C除了在TM7图像的离散指数比原始图像的大外，其余波段图像的离散指数均小于原始图像的离散指数，说明这2个模型对除TM7外的所有波段的图像有较好的校正效果。

从图7(b)可以看出，除了SCS模型和TF模型外，其他各模型在所有波段图像的同质系数均比原始图像的大，并且TF+C+坡度模型>C模型>TF+C模型，表明在校正后的图像中，TF+C+坡度模型最大程度地减少了像元之间的光谱异质性，校正效果最佳；C模型和TF+C模型的校正效果次之。而SCS模型和TF模型在TM1图像的同质系数要小于原始图像，并且这2个模型在所有波段的同质系数均小于另外3个模型的，表明这2个模型校正效果最差。

4 问题与讨论

4.1 系数C随波段和坡度的变化

从图2可以看出，对于同一波段的图像，系数C随着坡度的增加而增加。从式(3)可以看出，C对整个公式的计算结果起着调节的作用，系数C越大，对LH值的影响就越大；换言之，坡度越大，C的调节作用就越强。另外，对于TM1—TM4图像，当坡度越小时，系数C越接近0，表明对于这4个波段，坡度趋于平缓时，C的作用彻底消失或作用微弱；而对于TM5和TM7图像，系数C在主要坡度范围内较小，且均为负值，这主要是因为TM5和TM7图像的像元值较小，并且负的C值可以使LH值比没有引入C值时的LH更大，以增加阴影区域的光谱辐亮度。从图2还可以看出，对于同一坡度，系数C随着波段号的增加而减小。其原因是当波段号增加时，像元光谱辐射亮度值随之减小，较小的系数C及其范围可以避免C的调节作用过大而出现过度校正的现象。

4.2 检验结果的综合评价

在检验地形校正效果时，除利用校正后图像的均值、标准差以及像元值与光照系数的相关性等传统方法外，还引入了离散指数和同质系数的概念。离散指数可以反映像元值的离散程度，离散指数越小，校正效果就越好。从式(5)可以看出，当离散程度变小时，就要求均值增大的同时标准差要减小，所以离散指数变化涵盖了均值和标准差2个指标变化的涵义。因此，结合离散指数和均值、标准差能够更好地检验地形校正效果。同质系数则可反映像元之间的相似程度，良好的地形校正效果最大程度地减少了地形对像元的影响，使得同类地物像元的同质性提高，从而使图像整体同质系数增大。

在应用各模型校正后的图像中，TF+C+坡度模型校正后图像的均值增大而标准差减小，像元值与光照系数的相关性大大降低，离散指数减小而同质系数增加，并且各检验指标的值均比其余4种模型的更好。因此，综合所有的检验指标，TF+C+坡度模型的地形校正效果最好。

4.3 误差来源分析

DEM的质量及其与TM图像的几何配准精度是本文地形校正误差的最主要来源。国内已有学者进行过不同精度DEM对地形校正影响的分析，认为DEM的水平分辨率(像元大小)和垂直分辨率(高程间隔)的尺度效应往往构成地形校正误差的主要来源[15]。DEM与TM配准的精度决定了地形校正结果的可信度，DEM反映的是高程信息，而TM反映的是光谱信息，两者之间没有直接联系，很难找到同名地物点(特别是复杂地形区域)，因而导致在视觉上无法很精确地对两者进行几何配准。传统的配准方法通常采用基于地形图与TM图像的几何纠正来实现，但是用地形图数字化生成的DEM本身与源数据存在各种误差(人为误差、插值误差等)，因此，发展和建立一种DEM与遥感图像高精度配准的方法将是地形校正研究中亟待解决的问题。

5 结论

1)本文提出的基于Three Factor+C+坡度的地形校正模型在校正后图像的均值、标准差、像元值与光照系数的相关性、阴阳坡光谱辐亮度值、离散指数和同质系数等6个校正检验指标上均优于参与比较的SCS模型、SCS模型、Three Factor模型和Three Factor+C模型。

2)从总体上看，Three Factor+C+坡度模型的物理机制较为完善，加之引入了坡度分级和系数C的计算，使得其地形校正效果更好。实验证明，该模型可行且值得推广。

3)离散指数和同质系数作为较好的地形校正效果评价指标，也值得推广和采用。

4)DEM的质量及其与遥感图像的几何配准精度是地形校正误差的最主要来源。因此，发展和建立一种DEM与遥感图像高精度配准的方法将是地形校正研究中亟待解决的问题。

[1] Gao Y N,Zhang W C.Variable empirical coefficient algorithm for removal of topographic effects on remotely sensed data from rugged terrain[C]//IEEE International Geoscience and Remote Sensing Symposium,IGARSS 2007.Barcelona:IEEE,2007:4733-4736.

[2] Civco D L.Topographic normalization of Landsat Thematic Mapper digital imagery[J].Photogrammetric Engineering and Remote Sensing,1989,55(9):1303-1309.

[3] Teillet P M,Guindon B,Goodenough D G.On the slope-aspect correction of multispectral scanner data[J].Canadian Journal of Remote Sensing,1982,8(2):84-106.

[4] Gu D G,Gillespie A.Topographic normalization of Landsat TM images of forest based on subpixel sun-canopy-sensor geometry[J].Remote Sensing of Environment,1998,64(2):166-175.

[5] Zhang W C,Gao Y N.Topographic correction algorithm for remotely sensed data accounting for indirect irradiance[J].International Journal of Remote Sensing,2011,32(7):1807-1824.

[6] Smith J A,Lin T L,Ranson K L.The Lambertian assumption and Landsat data[J].Photogrammetric Engineering and Remote Sensing,1980,46(9):1183-1189.

[7] Tokola T,Sarkeala J,Van Der Linden M.Use of topographic correction in Landsat TM-based forest interpretation in Nepal[J].International Journal of Remote Sensing,2001,22(4):551-563.

[8] Soenen S A,Peddle D R,Coburn C A.SCS+C:A modified sun-canopy-sensor topographic correction in forested terrain[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(9):2148-2159.

[9] 亓雪勇,田庆久.山地TM遥感影像大气辐射校正模型改进及地表反射率反演[J].遥感信息,2007(4):3-8. Qi X Y,Tian Q J.Modification of atmospheric correction model and surface reflectance retrieval from TM imagery in rugged terrain[J].Remote Sensing Information,2007(4):3-8.

[10]高永年,张万昌.遥感影像地形校正物理模型的简化与改进[J].测绘学报,2008,37(1):89-94,120. Gao Y N,Zhang W C.Simplification and modification of a physical topographic correction algorithm for remotely sensed date[J].Acta Geodaetica et Cartographica Sinica,2008,37(1):89-94,120.

[11]Lu D L,Ge H S,He S Z,et al.Pixel-based minnaert correction method for reducing topographic effects on a Landsat 7 ETM+image[J].Photogrammetric Engineering and Remote Sensing,2008,74(11):1343-1350.

[12]Chander G,Markham B L,Helder D L.Summary of current radiometric calibration coefficients for Landsat MSS,TM,ETM+,and EO-1 ALI sensors[J].Remote Sensing of Environment,2009,113(5):893-903.

[13]Chavez P S.An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data[J].Remote Sensing of Environment,1988,24(3):459-479.

[14]Chavez P S.Image-based atmospheric corrections:Revisited and improved[J].Photogrammetric Engineering and Remote Sensing,1996,62(9):1025-1036.

[15]刘学军,卢华兴,仁政,等.论DEM地形分析中的尺度问题[J].地理研究,2007,26(3):433-442. Liu X J,Lu H X,Ren Z,et al.Scale issues in digital terrain analysis and terrain modeling[J].Geographic Research,2007,26(3):433-442.

(责任编辑：刁淑娟)

An improved topographic correction based on the Three Factor + C model

ZHANG Weige1,2,YANG Liao1,CAO Liangzhong1,2， JIA Yang1,2

(1.XinjiangInstituteofEcologyandGeography,ChineseAcademyofScience,Urumqi830011,China；2.UniversityofChineseAcademyofSciences,Beijing100049,China)

The topographic correction is the most critical component part of the remote sensing quantitative study of rugged terrain areas. According to the idea of slope grading in combination with the simplified Three Factor + C model,a Three Factor +C +Slope model was established to eliminate the defect of traditional and empirical topographic correction using the same coefficient as the slope changing. The results show that the Three Factor+C+Slope model is better than the C model,the SCS model,the Three Factor model and the Three Factor + C model in six calibration test indicators comprising the mean value,the standard deviation,the correlation between pixel value and illumination coefficient,the radiance discrepancy before and after correction,the dispersion index and the homogeneity coefficient. Due to its advantages such as excellent physical mechanism and considerable removal of the terrain effects on radiance,the Three Factor + C + Slope model is feasible and worthy of promotion.

topographic correction；Three Factor +C model；slope grading；dispersion index；homogeneity coefficient

2014-01-17；

2014-04-02

国家863项目“城市复杂时空数据集成分析与空间决策模拟”(编号：2013AA122302)和“国家科技基础平台-地球系统科学数据共享平台-新疆与中亚科学数据共享平台”共同资助。

10.6046/gtzyyg.2015.02.06

张伟阁，杨辽，曹良中，等.基于Three Factor+C模型改进的地形辐射校正方法[J].国土资源遥感，2015，27(2)：36-43.(Zhang W G,Yang L,Cao L Z，et al.An improved topographic correction based on the Three Factor + C model[J].Remote Sensing for Land and Resources，2015，27(2)：36-43.)

TP 751.1

A

1001-070X(2015)02-0036-08

张伟阁(1987-)，男，硕士研究生，主要研究方向为航空摄影测量与遥感应用。Email：zwg030369@163.com。