长沙市甲型H1N1流感流行干预措施效果的数学模拟*

陈田木刘如春张锡兴黄渊秀杨 洋胡国清△

长沙市甲型H1N1流感流行干预措施效果的数学模拟*

陈田木1刘如春1张锡兴1黄渊秀2杨 洋3胡国清2△

目的采用基于流行病学调查数据的动力学模型，模拟常用干预措施对控制长沙市甲型H1N1流感流行的效果。方法根据甲型H1N1流感疾病特征，建立易感者-潜伏期-显性／隐性感染者-移出者（susceptible-exposed-infectious／asymptomatic-removed，SEIAR）模型。在SEIAR模型基础上，依次构建包括隔离、治疗患者、疫苗接种等措施单独使用和联合使用的数学模型。采用长沙市实际疫情数据、暴发疫情数据、血清学调查数据、以及相关文献估算相关参数。采用软件Matlab7.1和Berkeley Madonna8.3.18实施模拟，采用累计罹患率（total attack rate，TAR）和累计感染率（total infection rate，TIR）指标评估干预效果。结果甲型H1N1流感的平均潜伏期为2.1天，平均病程为5.3天，隐性感染比例为41.54%，重症病例比例为3.11%，病死率为0.33%。长沙市甲型H1N1流感流行的基本再生数为1.81，无干预情况下流行导致的全人口TIR为73.98%、TAR为43.25%。每日隔离0.66%的患者和每日疫苗接种0.1%易感者能将TAR分别降低至29.70%和23.82%。隔离力度和疫苗接种力度越大，TAR越小。针对所有患者的治疗措施能将TAR降低至29.77%。综合干预措施效果的优劣顺序依次为：“隔离＋治疗患者＋疫苗接种”、“疫苗接种＋治疗患者”、“隔离＋疫苗接种”、“隔离＋治疗患者”。结论SEIAR模型可以较好地模拟流感流行的特点，流感流行时“隔离＋治疗患者＋疫苗接种”的综合干预措施效果最佳。

动力学模型 甲型H1N1流感 流行 隔离 抗病毒药物 疫苗接种

流感病毒由于频繁发生基因突变或RNA片段的重组［1］，极易引起流行或大流行［2－3］，对人类健康构成巨大威胁。国际上流感流行防控策略主要包括药物干预和非药物干预，前者主要指抗病毒药物和疫苗干预，后者主要指病例隔离、检疫、改善个人卫生行为、增加社交距离（如关闭学校、取消集体活动、不到人群聚集场所等）、旅游限制等［4］。然而由于缺乏无干预情况下的疫情数据，这些防控策略的效果很难通过传统的流行病学设计得以评价。因此，数学建模成为了制定和评估流感流行应对策略的重要手段［5－8］。

然而，绝大多数模拟研究未考虑流感潜伏期、隐性感染，所模拟干预措施的分类比较粗糙，对实际防控工作缺乏指导性［9－14］。本研究考虑流感潜伏期、隐性感染的特点，以长沙市甲型H1N1流感流行为例，建立无干预情况下城市流感流行的动力学模型。通过收集长沙市相关数据，估计模型参数。并在无干预的动力学模型的基础上，建立带干预措施的城市流感流行动力学模型，评估主要防控措施单独实施和联合实施的效果。

对象与方法

1.无干预的流感SEIAR模型

个体在流感发病过程中需一个易感、潜伏、染病、恢复／死亡的过程，且存在一定比例的隐性感染［15］。因此，适合使用易感者-潜伏期-显性／隐性感染者-移出者（susceptible-exposed-infectious／asymptomatic-removed，SEIAR）模型对甲型H1N1流感流行进行模拟。关于带隐性感染的流感动力学模型已有相关研究，Arino［16］等建立了封闭系统的SEIAR动力学模型，该模型未考虑人口出生和自然死亡以及因病死亡等。本研究以Arino等建立的SEIAR模型为框架，参照Longini等［17］的研究结果，结合长沙市人口出生和自然死亡、因病死亡等特点，建立长沙市流感SEIAR模型。模型用微分方程组表示为：

其中N、S、E、I、A、R分别表示总人口数、易感者、潜伏期者、显性感染者、隐性感染者、移出者，N（t）＝S（t）＋E（t）＋I（t）＋A（t）＋R（t）。dS／dt、dE／dt、dI／dt、dA／dt、dR／dt分别表示t时刻S、E、I、A、R各类人群的变化速率。μ、m、β、ω、γ、κ、p、c分别表示人口出生率、自然死亡率、传染率系数、潜伏期系数、移出率系数、与显性感染者相比隐性感染者传染力的大小系数、隐性感染比例、病死率。

2.带隔离的SEIAQR模型

本研究参照相关研究［18－19］，并结合无干预的SEIAR模型，建立SEIAQR模型。由于隐性感染者在疫情防控中难以被发现，故隔离措施只针对显性感染者I，隔离比例为φ，隔离后的人群为Q（isolation，Q）。在隔离期间，患者的病情发展过程与未隔离者相同。隔离者人群也会出现自然死亡现象，自然死亡率为m，因病死亡率为c。其余人群变化情况与无干预情况下的SEIAR模型相同。隔离患者的SEIAQR模型微分方程为：

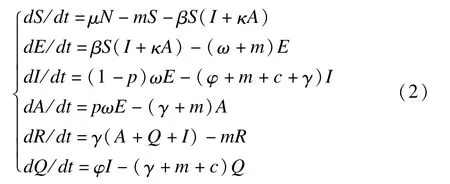
3.疫苗接种措施的SEIARV模型

假设只对易感者接种疫苗，接种比例为δ。易感者接种疫苗后变为疫苗接种人群。由于甲型H1N1流感疫苗接种单剂次10天后能产生保护性抗体［20］，因此接种疫苗后仍可能被感染。易感者S接种疫苗后，其易感性降低至原来的θ倍，设VES＝1-θ；其发病概率降低至原来的ψ倍，设VEP＝1-ψ，并且传染性将降低至原来的λ倍，设VEI＝1-λ。参考国外研究结果［21－22］，假设抗体水平维持时间大于流行的时间，由V人群变为易感者的比例对疫苗接种模拟结果影响较小，故在模拟疫苗接种效果时假定V人群不会向S人群转变。疫苗接种的SEIARV模型微分方程为：

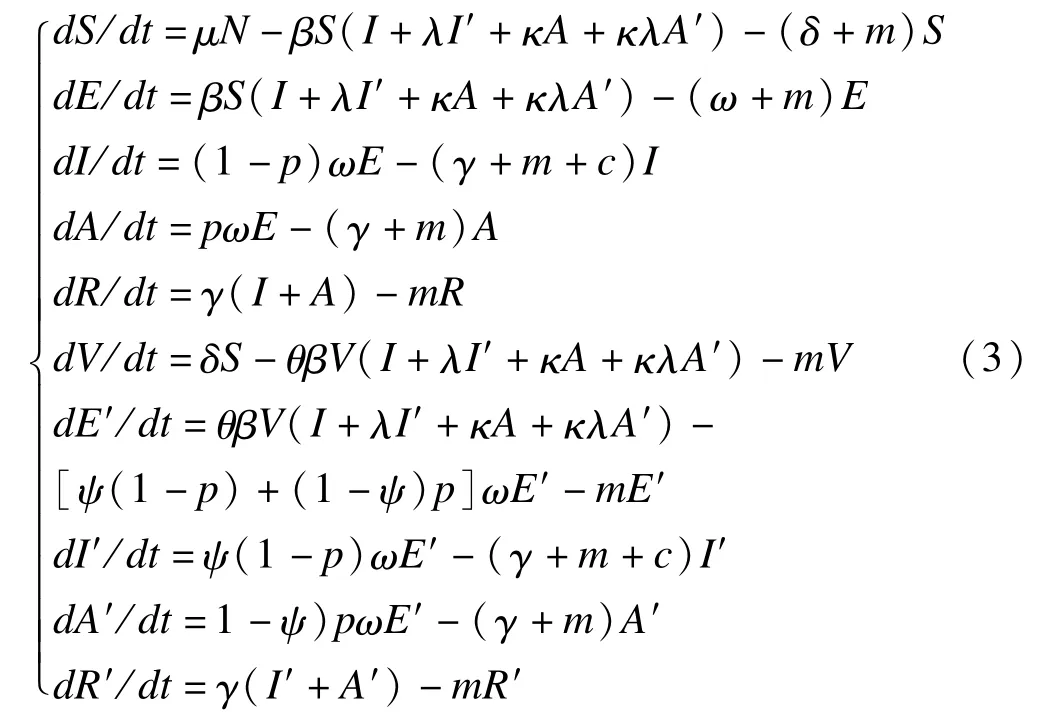
其中，E′、I′、A′、R′分别表示接种疫苗后被感染的潜伏期者、显性感染、隐性感染、移出者。根据Yang等［21］的研究，VES＝0.4，VEP＝0.67，VEI＝0.4。

4.抗病毒药物干预

在我国，实际应用的抗甲型H1N1流感病毒药物为奥司他韦（oseltamivir），故本研究仅评估服用奥司他韦的效果。2009年甲型H1N1流感流行期间，由于奥司他韦生产能力有限、价格昂贵，而且副作用比较大，故在实际应用中主要用于病例的治疗，几乎不用于预防。本研究将参照Longini等［17］的做法，假定如对某感染者给予规范抗病毒药物治疗，奥司他韦治疗时限为5天［17］，则该个体病程将缩短为未给药者的η倍，η的取值范围为0～1。在实际工作中，治疗措施仅被用于治疗患者，模型的微分方程组为：

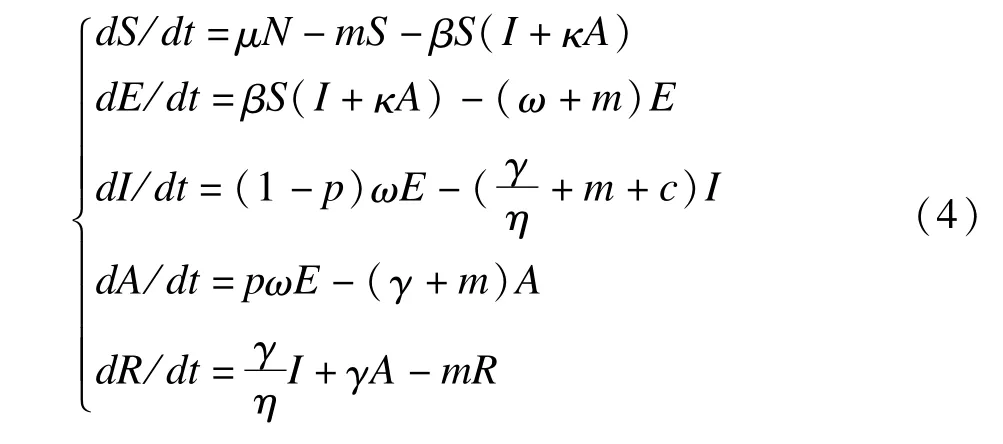
5.综合干预模拟

对于综合干预措施的效果而言，本研究模拟以上3类干预的4种组合。这些组合分别为：“隔离＋治疗患者”、“隔离＋疫苗接种”、“治疗患者＋疫苗接种”、“隔离＋治疗患者＋疫苗接种”。

6.资料收集内容与方法

（1）建立长沙市甲型H1N1流感流行疫情数据库

建立长沙市甲型H1N1流感流行疫情数据库，收集长沙市2009年流感流行的首例病例至末例病例的资料，时间范围为2009年5月22日至2010年3月13日，资料来自中国疾病预防控制信息系统。病例的诊断标准为《甲型H1N1流感诊疗方案（2009年第一至三版）》［23］。病例包括轻症病例、重症病例、死亡病例。另外，本研究还收集流行早期的所有输入性病例资料，计算基本再生数R0和传染率系数β。

（2）建立长沙市甲型H1N1流感暴发疫情数据库

收集2009年5月至2013年3月30日，长沙市辖区内所有甲型H1N1流感暴发疫情资料，建立“长沙市甲型H1N1流感暴发疫情数据库”。用于计算甲型H1N1流感病程和估计潜伏期，求解参数γ和ω。暴发疫情处置按照《中国流感监测方案（2010年版）》［24］和卫生部《流感样病例暴发疫情处置指南（2012版）》［25］，并采集病例的咽拭子标本进行甲型H1N1流感病毒核酸PCR检测。病例诊断标准为卫生部《流行性感冒诊断与治疗指南（2011年版）》［26］。

（3）建立长沙市甲型H1N1流感血清学调查数据库

建立长沙市甲型H1N1流感血清学调查数据库，收集人群流感血清学调查资料，调查对象为长沙市城区内的常住人群。采用从“市、县／区、居委会、户、个体”多阶段随机抽样的方法抽取研究对象，按照“0～5岁”，“6～15岁”，“16～24岁”，“25～59岁”，“60岁及以上”5个年龄组抽取1500名对象，各年龄组约300人。对于≥18岁成人，要获得本人的知情同意；对于＜18岁的未成年人，获得本人及其父母或法定监护人的知情同意。按照统一调查问卷，对每个确定的调查对象进行个案调查。采集每名调查对象静脉血5m l，对不足6周岁的儿童采集静脉血2～3m l，离心获得每名调查对象的血清标本。利用血凝抑制（HI）方法对标本进行检测，血清HI抗体效价≥1∶40为抗体阳性。

7.参数估计与初始值设定

查阅2011年《长沙市统计年鉴》［27］，收集2009年长沙市人口数、出生率、自然死亡率等数据，获得μ、m。参照相关研究［8，17，20，26］，获得流感隐性感染者的传播能力、接种疫苗后个体产生抗体的时间等资料，即κ、f的值。资料显示隐性感染者也具有传染性［8，17，26］，且隐性感染者的传染力为显性感染者的一半［8，17］，因此κ＝0.5。研究显示，甲型H1N1流感疫苗接种单剂次，10天后能产生保护性抗体［20］，因此f＝0.1。通过分析“长沙市甲型H1N1流感流行疫情数据库”资料可获得病死率c。

利用2009年长沙市流感流行早期所有输入性病例资料，根据“方程（5）”可以计算每一例病例的基本再生数［28-31］（basic reproduction number，R0），然后计算所有输入性病例的基本再生数的平均值，进而估算输入性甲型H1N1流感在长沙市的传播力度大小。根据定义，基本再生数基本R0公式表达如下：

根据“方程（6）”计算传染率系数β。可以根据其自身定义、同时参照Chen等［32］和Arino等［16］的做法，“模型（1）”中基本再生数基本R0公式表达如下：

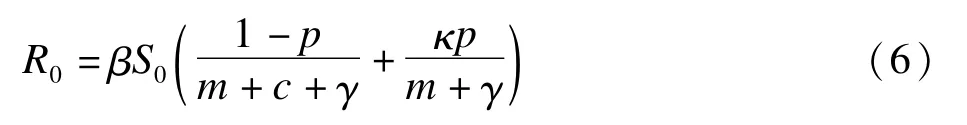
其中h为每日由某病例传染导致的新发病例数，l为传染源的自然病程。

利用流感病例的病程资料进行参数γ求解；选择达到突发公共卫生事件级别的疫情数据进行甲型H1N1流感拟合，求解参数ω。本研究以数据库中17起疫情为基础数据，分别收集其未采取干预措施时的每日新增病例数资料，利用“模型（7）”进行曲线拟合，估计参数ω。

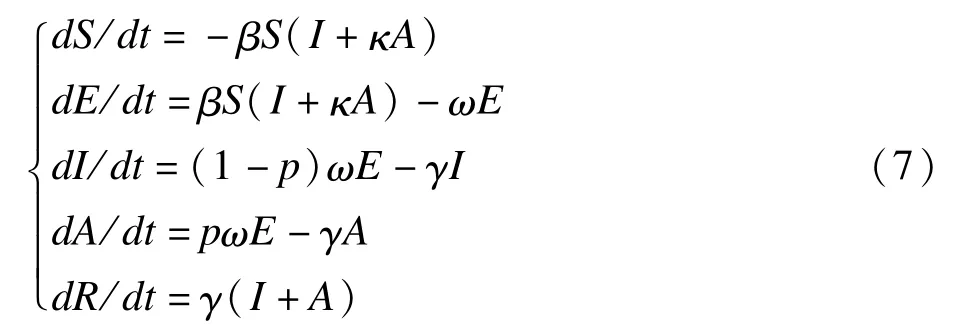
本研究利用血清学调查数据库资料估算人群甲型H1N1流感隐性感染率p。参照相关研究［17，33］，对某感染者给予规范抗病毒药物治疗，奥司他韦治疗时限为5天，则该个体病程比未给药者缩短约1天，因此，η＝1-γ＝0.8113。

实际隔离力度φ具体数值通过疫情数据库和血清学调查数据库计算获得。实际疫苗接种力度δ具体数值通过血清学调查数据库获得。另外，为了更全面了解不同隔离力度、疫苗接种力度对疫情防控效果影响，设定不同φ、δ取值进行模拟。

8.数据处理与模型模拟方法

相关数据的录入和管理、以及相关制图均采用excel 2003。有、无干预措施下的疫情模拟采用的软件为Matlab7.1和Berkeley Madonna8.3.18。

结 果

1.长沙市甲型H1N1流感流行过程

2009年5月26日，长沙市报告首例甲型H1N1流感确诊病例，该例的发病时间为5月22日（图1横坐标的第0天），之后陆续有输入性病例出现。7月底开始出现本地感染病例，9月4日开始出现本地小规模传播，并在9月4日－16日出现一个小高峰，9月7日出现首起暴发疫情。自10月9日起长沙市开始出现大范围流行，11月中旬出现明显的发病高峰，之后疫情开始下降，2010年1月份恢复到较低水平，1月21日长沙市甲型H1N1流感流行结束，之后仅有个别病例报告。整个流行过程历时244天，累计报告发病6908例，累计报告发病率为112.33／10万，其中重症病例215例，占总病例数的3.11%，死亡23例，病死率为0.33%。

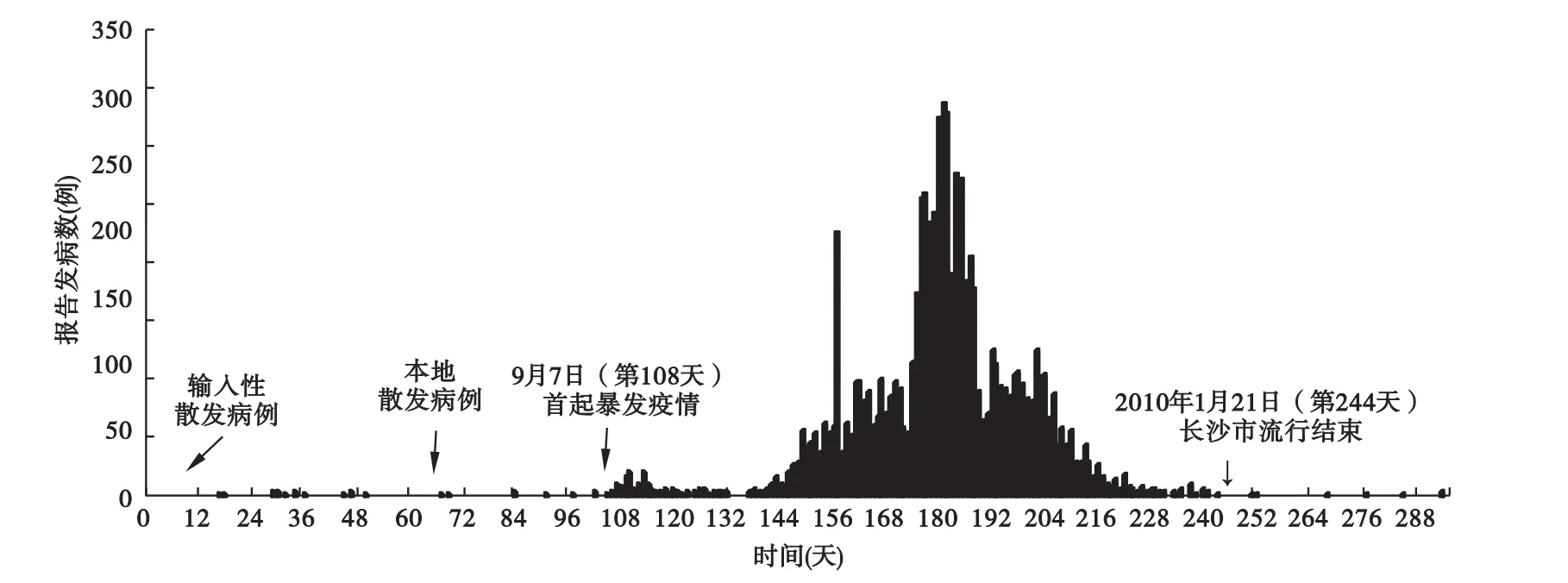
图1 长沙市2009年甲型H1N1流感流行过程

2.甲型H1N1流感自然史

从疫情数据库中选出的2起暴发疫情共有病例89例，病程最长10天，最短2天，平均病程为5.3（5.3± 1.96）天，移出率系数γ＝0.1887。根据疫情数据库中17起疫情的无干预时期（疾控未介入之前）的疫情数据，采用“模型（7）”进行曲线拟合可知，甲型H1N1流感病例平均潜伏期为2.1天，ω＝0.4766。

现场调查结果显示，1500名调查者中接种过甲型H1N1流感疫苗者288人，接种比例为19.20%。未接种过甲型H1N1流感疫苗人群中抗体阳性的有337人，抗体阳性率27.81%。未接种疫苗的337名甲型H1N1流感抗体阳性者，140名抗体阳性者在2009年5月至2010年1月期间未出现流感相关症状，属于隐性感染者，故隐性感染比例为41.54%，即p＝0.4154。

3.甲型H1N1流感的传播能力

根据疫情数据库资料，2009年长沙市甲型H1N1流感输入期共有甲型H1N1流感病例20例。在疾控部门未介入调查期间之前（无干预期间），与20例患者密切接触的有305人，造成续发病例7例。根据基本再生数的定义［28－31］，基本再生数＝无干预期间的续发病例数÷无干预天数×自然病程，算得20例病例的基本再生数均值为1.81。

4.无干预情况下的甲型H1N1流感SEIAR模型模拟

模拟结果显示，在无干预情况下，输入性病例会造成长沙市甲型H1N1流感流行，疫情的高峰日为第150天（2009年10月19日），疫情持续301天，累计发病2775587例，罹患率高达43.25%，累计隐性感染者1972253人，占总人口的30.73%，累计感染者4747840，感染率高达73.98%。

5.各类干预措施的效果模拟

（1）隔离的效果

根据血清学调查数据及实际报告的病例数计算可知，实际隔离力度仅为0.66%。本研究模拟实际隔离力度，以及隔离力度分别为0.5%、1%、1.5%、2%时隔离措施的效果。模拟结果显示，当每日隔离比例为病例总数的0.5%（φ＝0.005）时，疫情高峰日为第155天（2009年10月25日），与无干预相比推后5天，累计罹患率为29.89%。隔离力度越大，累计发病人数越少，疫情高峰越低，高峰日越推后，流行周期越长。当每日隔离比例为病例总数的2.0%（φ＝0.020）时，与无干预相比疫情高峰日推后15天，疫情持续时间为361天，累计罹患率降低至28.28%。

（2）药物干预的效果

研究结果显示，若对每一例病例均实施奥司他韦规范治疗，则长沙市甲型H1N1流感流行疫情将会有所缓解，累计罹患率将低至29.77%，疫情高峰下降并推后，流行周期延长。

（3）疫苗接种的效果

根据血清学调查结果可知，至流行结束累计约有19.20%人群接种了流感疫苗，即δ＝0.00099032，该接种力度非常接近0.001。本研究模拟疫苗接种力度分别为0.05%、0.10%、0.15%、0.20%时隔离措施的效果。结果显示，当每日接种比例为易感者总数的0.05%（δ＝0.0005）时，与无干预相比疫情高峰推后9天，累计罹患率为27.45%。接种力度越大，累计发病人数越少，疫情高峰越低，高峰日越推后，流行周期越长。

（4）综合干预的效果

由图2和表1可知，“隔离＋治疗患者”和“隔离＋疫苗接种”这两类综合干预措施的疫情高峰时间、高峰值、疫情持续时间均相当，但前者的效果会更好。而“疫苗接种＋治疗患者”和“隔离＋治疗患者＋疫苗接种”这两类综合干预措施的疫情高峰时间、高峰值、疫情持续时间均相当，且优于其他两类综合干预措施，但“隔离＋治疗患者＋疫苗接种”的峰值更低。

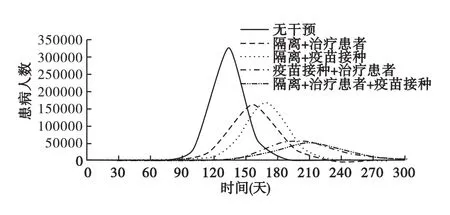
图2 各类综合干预措施的效果模拟

6.敏感性分析

本研究模拟了基本再生数取值为1.3～2.5时，累计罹患率的变化情况。模拟结果显示，当R0为1.3时，累计罹患率为24.5%，随着R0的增大，累计罹患率也增加，当R0为2.5时，累计罹患率为52.0%。说明基本再生数对累计罹患率存在较大影响。

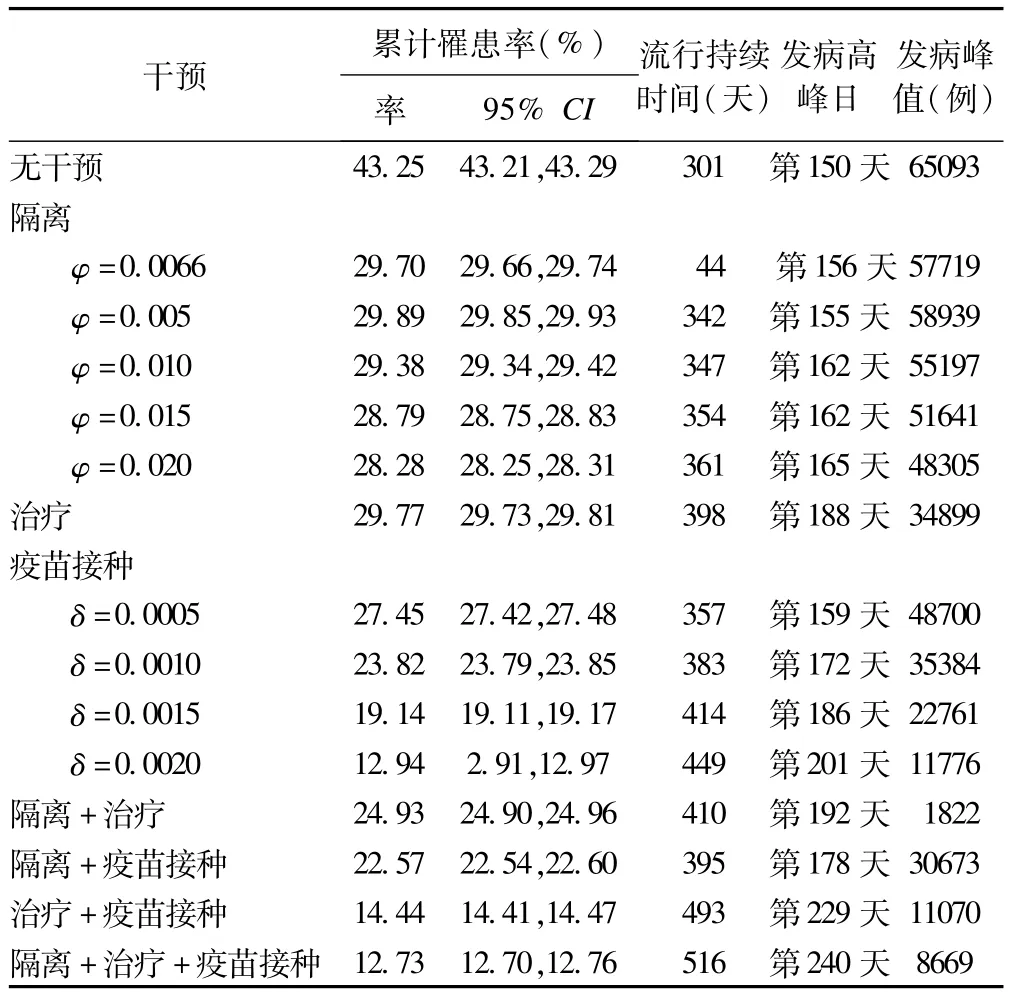
表1 各类干预措施和综合干预措施的效果模拟

讨 论

1.流行强度与模型合理性

本研究计算获得甲型H1N1流感的平均潜伏期为2.1天，平均病程为5.3天，隐性感染比例为41.54%，基本再生数为1.81，与国际公认取值略有差异［8，14，15，17，21，34，35］，但这些参数是通过实际数据计算获得的，用于长沙市的流感数学建模更加合适。

模拟结果显示，在输入性甲型H1N1流感的基本再生数R0为1.81时，流感流行导致的长沙市全人口的累计罹患率为43.25%。敏感性分析结果显示，本研究模拟的流感基本再生数取值在1.3～2.5之间变化时，引起的累计罹患率为24.5%～52.0%，这与已发表的大部分研究结果较为接近［21，36，37］，与个别结果存在一定的差异［38］，如Milne等研究结果显示当基本再生数对累计罹患率影响的敏感性分析R0为2.5时，累计罹患率高达64.8%，这种差异可能是采用的隐性感染比例不同导致的，具体原因尚待进一步研究。

2.干预措施的效果

本研究结果显示，隔离、疫苗接种力度越大，累计发病人数越少，疫情高峰越低，高峰日越推后，流行周期越长，这与国际上相关研究结果类似［39－40］。研究结果还显示，若对每例病例进行奥司他韦规范治疗，疫情会有所缓解。然而，在实际工作中，受医疗机构数量、诊疗条件、实验室诊断能力、以及个体行为等多种因素的影响，被发现病例往往只占实际总发病数的很小一部分。在这种情况下，隔离措施将难以被卫生部门实施。因此，在实际防控工作中，需要患者的主动参与。如个体出现发热、咳嗽或咽痛等流感样症状时，应自行做好居家隔离。在实际工作中很难做到疫苗接种的最大化。疫苗接种受疫苗生产和储备能力、个体的参与度、疫苗接种门诊数量和最大负荷量等多种因素限制。因此，在日常工作中，政府部门应考虑提高疫苗生产和储备能力、发动市民积极参与疫苗接种、提高接种门诊的工作负荷量等，最大程度地对易感者接种疫苗。

不同干预措施效果的比较显示，“隔离＋治疗患者＋疫苗接种”、“疫苗接种＋治疗患者”、“隔离＋治疗患者”、“隔离＋疫苗接种”的效果依次降低。在这些措施中，治疗患者和疫苗接种均为药物干预措施，而隔离属于非药物干预。三类措施同时采取的效果最好，若只采取两种干预措施，则药物干预措施的组合效果优于药物干预和非药物干预的组合效果。

从长沙市实际疫情控制效果看（累计感染率27.81%），实际防控措施取得了较好的效果，这主要依赖于疫情早期的严格检疫和中后期的疫苗接种和暴发疫情处置。但从模拟结果看，若能每日为0.1%的人口接种疫苗并治疗所有患者，可将人群累计罹患率降至14.44%；若在此基础上每日隔离0.66%患者，可以将人群累计罹患率进一步降至12.73%。由此可见，长沙市流感防控工作尚有改进余地。未来应对类似疫情，可考虑将数学模拟结果作为参考，以提高防控工作的效率。本研究存在以下局限性。首先，本研究仅从全人群角度模拟防控策略效果，未考虑年龄的影响。其次，本研究未考虑气候和人群社会流动等因素的影响，这可能在一定程度上影响建模的效果。

1.Russell CJ，Webster RG.The genesis of a pandemic influenza virus. Cell，2005，123（3）：368-371.

2.Belser JA，Bridges CB，Katz JM.Past，Present，and Possible Future Human Infection with Influenza Virus A Subtype H7.Emerg Infect Dis，2009，15（6）：859-865.

3.World Health Organization.Pandemic（H1N1）2009-update 112.http：／／www.who.int／csr／don／2010_08_06／en／index.html.

4.Lee VJ，Lye DC，Wilder-Smith A.Combination strategies for pandemic influenza response-a systematic review of mathematical modeling studies.BMC Medicine，2009，7：76.

5.Wu JT，Cow ling BJ.The use of mathematical models to inform influenza pandemic preparedness and response.Exp Biol Med（May wood），2011，236（8）：955-61.

6.刘东辉，汪兴太，庄辉.2009年猪源性甲型流感大流行的公共卫生介入管理.中国预防医学杂志，2010，11（2）：109-112.

7.Cruz-Pacheco G，Duran L，Esteva L，et al.Modelling of the influenza A（H1N1）v outbreak in Mexico city，April-May 2009，with control sanitary measures.EUROSURVEILLANCE，2009，14（26）：1-3.

8.Germann TC，Kadau K，Longini IM Jr，et al.Mitigation strategies for pandemic influenza in the United States.Proc Natl Acad Sci USA.，2006，103（15）：5935-40.

9.刘俊先，石秀文.流行性感冒的微分方程模型及数据分析.数学实践与认识，2009，39（14）：234-237.

10.苏蕊.具有年龄结构的传染病SIR流行病模型的研究.数学的实践与认识，2011，41（6）：140-143.

11.赵爱娟.甲流病毒传播的年龄结构模型的稳定性.数学的实践与认识，2011，41（20）：112-118.

12.倪莉红，Wu J.流感大流行期间疫苗免疫方案的传染病模型.热带医学杂志，2010，10（11）：1340-1343.

13.肖洪，张锡兴，朱佩娟，等.《学校甲型H1N1流感防控工作方案》应用实例与定量评价.实用预防医学，2011，18（7）：1184-1186.

14.Tracht SM，Valle SYD，Hyman JM.Mathematical Modeling of the Effectiveness of Facemasks in Reducing the Spread of Novel Influenza A（H1N1）.PLoSone，2010，5（2）：1-12.

15.Longini IM Jr，Halloran ME，Nizam A，Yang Y.Containing pandemic influenza with antiviral agents.Am J Epidemiol，2004，159（7）：623-33.

16.Arino J，Brauer F，Driessche P van den，et al.Simple models for containment of a pandemic.J.R.Soc.Interface，2006，3：453-457.

17.Longini IM Jr，Nizam A，Xu S，et al.Containing pandemic influenza at the source.Science，2005，309（5737）：1083-1087.

18.Feng Z，Thieme HR.Recurrent outbreaks of childhood diseases revisited：the impact of isolation.Math.Biosci，1995，128：93-130.

19.Hethcote H，Ma Z，Liao S.Effects of quarantine in six endemic models for infectious diseases.Math.Biosci，2002，180：141-160.

20.Sun Y，Bian C，Xu K，et al.Immune Protection Induced on Day 10 Following Administration of the 2009 A／H1N1 Pandemic Influenza Vaccine.PLoSONE，2010，5（12）：e14270.

21.Yang Y，Sugimoto JD，Halloran ME，et al.The Transmissibility and Control of Pandemic Influenza A（H1N1）virus.Science，2009，326：729.

22.Ferguson NM，Cummings DAT，Fraser C，et al.Strategies for mitigating an influenza pandemic.Nature，2006，442（27）：448-452.

23.中华人民共和国卫生部.甲型H1N1流感诊疗方案（2009年第一至第三版、2010年版）.2009，2010.

24.中华人民共和国卫生部.中国流感监测方案（2010年版），2010.

25.中华人民共和国卫生部.流感样病例暴发疫情处置指南（2012版），2012.

26.中华人民共和国卫生部.流行性感冒诊断与治疗指南（2011年版），2011.

27.长沙市统计局.《长沙统计年鉴》.长沙，2011.

28.Coburn BJ，Wagner BG，Blower S.Modeling influenza epidemics and pandemics：insights into the future of swine flu（H1N1）.BMC Medicine，2009，7：30.

29.Mikolajczyk R，Krumkamp R，Bornemann R，et al.Influenza-Insights from Mathematical Modelling.Dtsch Arztebl Int，2009，106（47）：777-82.

30.徐文雄，张仲华.年龄结构SIR流行病传播数学模型渐进分析.西安交通大学学报，2003，37（10）：1086-1089.

31.陈田木，刘如春，王琦琦，等.SIR模型在一起校园急性出血性结膜炎暴发疫情处理中的应用.中华流行病学杂志，2011，32（8）：723-726.

32.Chen SC，Liao CM.Modelling control measures to reduce the impact of pandemic influenza among schoolchildren.Epidemiol.Infect，2008，136：1035-1045.

33.王孟昭，孙武装，王亚梅，等.磷酸奥司他韦治疗流行性感冒的临床疗效和安全性.中华传染病杂志，2003，21（2）：114-117.

34.陈雄飞，董晓梅，肖新才，等.新型甲型H1N1流感症状持续时间及其影响因素分析.中国卫生统计，2012，29（6）：812-815.

35.陈雄飞，李铁钢，柳洋，等.新型甲型H1N1流感潜伏期及其影响因素分析.中国卫生统计，2011，28（4）：357-360.

36.Ferguson N，Cummings D，Cauchemez S，et al.Strategies for containing an emerging influenza pandemic in Southeast Asia.Nature，2005，437：209-214.

37.Glass R，Glass L，Beyeler W，et al.Targeted social distancing design for pandemic influenza.Emerg Infect Dis，2007，12：1671-1681.

38.Milne GJ，Kelso JK，Kelly HA，et al.A small community model for the transmission of infectious diseases：comparison of school closure as an intervention in individual-based models of an influenza pandemic.PLoS One，2008，3（12）：e4005.

39.Kelso JK，Milne GJ，Kelly H.Simulation suggests that rapid activation of social distancing can arrest epidemic development due to a novel strain of influenza.BMC Public Health，2009，9：117.

40.Lee BY，Brown ST，Cooley PC，et al.A Computer Simulation of Employee Vaccination to Mitigate an Influenza Epidemic.Am J Prev Med，2010，38（3）：247-257.

（责任编辑：丁海龙）

Simulating the Effects of Intervention Strategies on the Epidemic of Influenza A（H1N1）Using Dynamic Model in Changsha City

Chen Tianmu，Liu Ruchun，Zhang Xixing，et al.（Changsha Center for Diseases Control and Prevention（410001），Changsha）

ObjectiveTo simulate the effects of interventions of isolation，antivirus and vaccination on the epidemic of influenza A（H1N1）in Changsha city using dynamical model.MethodsBased on the history of influenza A（H1N1），we built a susceptible-exposed-infectious／asymptomatic-removed（SEIAR）model.Then，intervention-specific models were developed，including isolation，antivirus drug，vaccination and combined interventions.Key parameters of models were estimated based on epidemiological data，outbreak data，and serological survey data and related literature.We did the simulation using Matlab 7.1 and Berkeley Madonna 8.3.18.Total attack rate（TAR）and total infection rate（TIR）were used to assess the effects of interventions.ResultsThe average incubation period and the average infectious period of influenza A（H1N1）was2.1 days and 5.3 days，respectively.41.54%of infected persons were asymptomatic.3.11%of symptomatic patients had severe symptoms and the case fatality rate was0.33%.The basic reproduction number（R0）of influenza A（H1N1）pandemic was1.81 in Changsha city.without interventions，the TIR and TAR would be 73.98%and 43.25%，respectively.The TAR would decrease to 29.70%and 23.82%if0.66%of the infected were isolated and 0.1%of the susceptible were vaccinated each day separately.Strong quarantine and vaccination would lead to small TAR.The TAR would fall to 29.77%if all patients received antivirus drug treatment. The effects of combined interventions decreased as follow：‘isolation＋antivirus drug＋vaccination’，‘antivirus drug＋vaccination’，‘isolation＋vaccination’and‘isolation＋antivirus drug’.ConclusionSEIAR model can well simulate the transmission of influenza A（H1N1）epidemic.The combination of isolation，antivirus drug and vaccination can maximally control the transmission of influenza A（H1N1）.

Dynamic model；Influenza A（H1N1）；Pandemic；Isolation；Antivirus；Vaccination

湖南省卫生厅科研项目（B2012-138）；长沙市科技局科研项目（K1205028-31）资助

1.长沙市疾病预防控制中心（410001）

2.中南大学公共卫生学院流行病与卫生统计学系

3.佛罗里达大学公共卫生学院生物统计学系

△通信作者：胡国清，E-mail：huguoqing009＠gmail.com