基于干扰观测器的高超飞行器反演多滑模控制*



基于干扰观测器的高超飞行器反演多滑模控制*

唐意东，李小兵，雷虎民

(空军工程大学 防空反导学院，陕西 西安710051)

摘要：针对高超声速飞行器匹配/非匹配不确定性控制问题，建立了高超声速飞行器纵向运动三角标准型模型。引入非线性干扰观测器，结合反演控制解决非匹配不确定性控制问题的优势，设计了一种基于反演控制的飞行器多滑模控制器。该方法首先利用非线性干扰观测器的逼近特性对系统受到的干扰进行观测，在每一步反演设计中引入滑模控制设计反演多滑模控制器，从而实现系统对控制指令的输出跟踪。仿真结果表明该方法能够较准确地进行干扰观测，保证了系统的稳定性和鲁棒性，具有良好的控制性能。

关键词：高超声速；非线性干扰观测器；不确定性；反演控制；滑模控制

0引言

近年来，在核武器裁减背景下，高超声速飞行器作为未来新的非核战略威慑力量迅速成为研究热点。但是，由于高超声速飞行器飞行环境变化范围大，机身的弹性变形、气动参数变化和外界干扰都不可避免，致使所建立的飞行器数学模型存在高度非线性、强耦合及不确定性且表现为非匹配不确定性[1]。因此，研究如何在系统存在匹配/非匹配不确定性和外界干扰的情况下，实现系统的稳定跟踪控制具有重要的现实意义。

非线性控制方法的发展为解决高超声速飞行器控制问题提供了有效的途径。滑模控制因其独特的鲁棒性、对匹配不确定性和外界干扰的完全自适应性等特点[2-3]，被广泛应用于各个领域以解决不确定非线性系统的控制问题。文献[4]采用自适应方法估计模型中的不确定参数，基于动态逆方法设计内环控制器，采用滑模控制方法设计外环控制器，得到了一种双环滑模控制方法。Yuri Shtessel和McDuffie Y等[5]利用欧拉方程描述X-33再入大气层时的动力学模型，分别设计内/外环滑模控制器，实现对角度和角速度指令的跟踪。文献[6]设计鲁棒滑模观测器对系统的不确定性及未知干扰进行在线估计，并设计滑模变结构控制器对不确定性进行抑制，最终实现对参考指令的鲁棒输出跟踪。然而，采用常规滑模控制解决不确定性控制问题时，要求不确定性满足匹配条件[7]。而反演设计方法采用递归设计方法，在解决系统非匹配不确定性控制问题方面具有明显的优势。文献[8]基于气动与推进参数向量的有界自适应估计律，设计了反演鲁棒控制律，保证了闭环系统的稳定性。文献[9-10]使用神经网络对飞行参数误差等不确定因素进行补偿，在此基础上设计了飞行器自适应反演控制器。同时，滑模控制往往需要较大的切换增益来消除外加干扰和不确定性的影响，这必然会增大控制中的抖振，利用干扰观测器对外界干扰进行估计，并加以补偿成为解决抖振问题的重要研究方向[11]。文献[12]在设计反演控制器的过程中，设计了超扭曲滑模干扰观测器，实现了对系统不确定性的估计和补偿，提高了系统的性能。文献[13]利用非线性干扰观测器削弱系统不确定性和外界干扰的影响，并运用到导弹的控制器设计中，增强了系统的鲁棒性。

本文首先建立高超声速飞行器纵向运动三角标准型模型，再次基础上利用反馈线性化方法对模型进行线性化处理，结合滑模变结构控制和反演设计思想，并基于趋近律和非线性干扰观测器设计了一种反演多滑模控制器。最后通过干扰作用下参考指令跟踪控制的对比仿真验证研究，验证该方法的有效性和优越性。

1高超声速飞行器纵向平面三角标准型模型建立

1.1纵向运动模型描述

在巡航条件下，只考虑高超声速飞行器的纵向运动。系统的控制输入为升降舵偏角δe和油门开度βc。状态量为飞行速度v、飞行高度h、航迹角γ、攻角α和俯仰角速率q。将弹性振动的影响计入气动参数拟合误差当作不确定性处理，建立高超声速飞行器的纵向动力学模型为

式中：μ为重力常数；M为地球质量；m，Iy分别为飞行器的质量和俯仰转动惯量；L，T，D，My分别为升力、推力、阻力和俯仰力矩；r为飞行器距离地球中心的距离。其表达式分别为

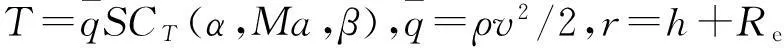
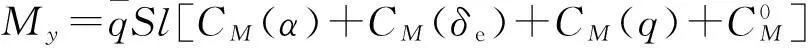
式中：Re为地球半径；S，l为飞行器参考气动面积和气动弦长，；ρ为空气密度；CL，CD，CT分别为升力系数、阻力系数和推力系数；CM(α)，CM(δe)和CM(q)分别为由攻角、升降舵偏角和俯仰角速率引起的俯仰力矩系数。

在给定马赫数情况下，忽略舵面偏转对升力和阻力的影响，假设在飞行高度和攻角变化范围不大时，力和力矩系数关于状态量之间的关系式可由一次线性函数逼近，即

(6)

式中：β为发动机油门开度调定，与发动机燃流率WF相关。式中关于控制量和状态量多项式的具体形式见文献[14]。

参照文献[15]对发动机模型的简化，将高超声速飞行器发动机模型等效为一个二阶系统模型：

(7)

式中：ξ和ωn分为二阶系统模型的阻尼和频率；βc为发动机油门开度。

1.2模型三角标准型表示

控制系统的任务是使得系统输出v和h在控制输入的作用下跟踪速度和高度参考指令vd和hd。通过对式(3)的逆变换，将理想高度指令hd转化为理想的航迹角指令θd，可以通过对航迹角参考指令的跟踪来实现高度控制。此时，在短周期巡航控制中，航迹角跟踪误差累计造成的高度误差不会太大，控制效果是可靠的。通过这种逆运算，可以实现模型的降阶，尽管只降阶一次，但是却能够大大简化在控制器设计过程中的连续求导运算。对降阶处理后的高超声速飞行器动力学模型，选取自变量XT=(v,γ,α，q，β，βT)， 令

最终得到高超声速飞行器的纵向运动模型为

(8)

式中：βT为临时定义的发动机状态量。

高度25 km时，速度指令变化30 m/s，高度变化300 m对声速的影响为0.6‰，对空气密度的影响为4‰，对动压的影响为0.52%。因此，在巡航条件下声速和动压可以视作常值，可通过标准大气表[16]查得。另外，高速变化对于距离r的影响也可以忽略，即r=Re+h为常值。将高超声速飞行器不

确定性转化为参数的不确定性问题：

l=24.384(1+Δl)m,S=334.73(1+ΔS)m2，

ρ=0.028 3(1+Δρ)kg/m3,m=95 340(1+Δm)kg，

Iy=1.17×107(1+ΔIy)kg·m2.

控制器的目标是在考虑上述模型参数不确定性和外界干扰的情况下，实现飞行器的飞行航迹角和速度对给定参考期望指令的跟踪。

2反演滑模控制律设计

2.1高超声速飞行器模型反馈线性化

选取自变量zT=(v,γ，α，β)，采用反馈线性化方法对速度v和航迹角γ进行输入-输出线性化处理，即分别连续求导3次，可以得到

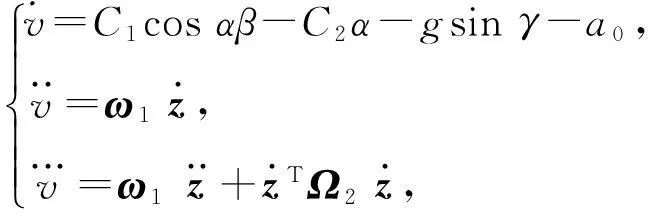
(9)

(10)

α和β的二阶导数由两部分组成，即控制相关部分和控制不相关部分：

(11)

(12)

(13)

(14)

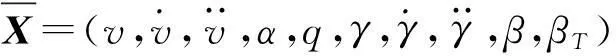
(15)

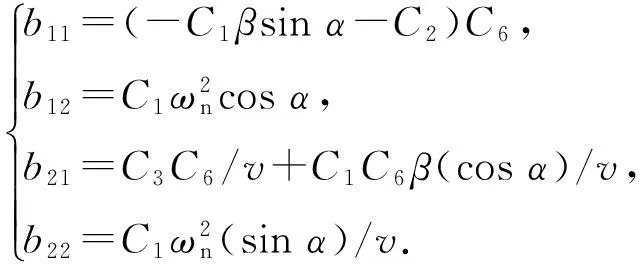
(16)

2.2非线性干扰观测器设计

基于非线性干扰观测器的反演滑模控制原理框图如图1所示[17]。

图1　基于非线性干扰观测器的反演滑模控制原理框图Fig.1　Structure diagram of backstepping SMC　　　 based on NDO

考虑速度跟踪控制非线性子模型，定义干扰观测器状态

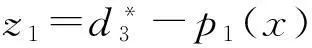
(17)

设计速度跟踪通道的非线性干扰观测器为

(18)

为简化问题，通常将L1(x)取为常数L0，即p1(x)=L0x3。

同理，可以得到航迹角跟踪通道的非线性干扰观测器为

(19)

2.3反演滑模控制律设计

考虑式(14)所示的具有不确定性的系统，做如下假设：

假设1参考指令及其三阶导数存在且有界；

(20)

在反演滑模控制律设计时，增加定义系统误差：

(21)

式中：x2d，x3d，x7d，x8d为反演设计过程中引入的虚拟控制量。

(22)

(23)

(24)

2.4稳定性分析

定义Lyapunov函数

V=V1+V2，

(25)

(26)

(27)

对式(26)求导得：

(28)

将式(22)，(23)代入式(28)得到

(29)

将式参数自适应律代入式(29)得

3仿真验证

为验证干扰观测器和控制器的性能，将传统滑模控制律和反演滑模控制进行对比仿真。在系统中加入5%的参数摄动，在[10,15] s，[15,20] s分别在速度跟踪控制通道、航迹角跟踪控制通道加入非匹配干扰d1=1，d2=3sint，d6=0.01，d7=0.05sin(5πt)；t>25 s，t∈[30,40] s时分别在速度跟踪通道、航迹角跟踪通道加入匹配干扰d3=4.5，d8=0.5。仿真结果如图2~12所示。

仿真结果表明，不确定性和干扰对系统影响显著，传统滑模控制对匹配不确定性具有一定的抑制作用，但是控制输入量存在幅值较大的激变。在反演滑模控制器的作用下，系统能够更好地克服系统中的不确定性和外界干扰，实现对参考指令的准确跟踪。由图8~9可以看到，虚拟控制量能实现对速度变化率和航迹角速率的良好跟踪，便于将中间变量用于相关的设计过程。由图10~11可以看到，设

图2　速度指令跟踪响应曲线Fig.2　Response of speed command tracking

图3　航迹角指令跟踪响应曲线Fig.3　Response of track angle command tracking

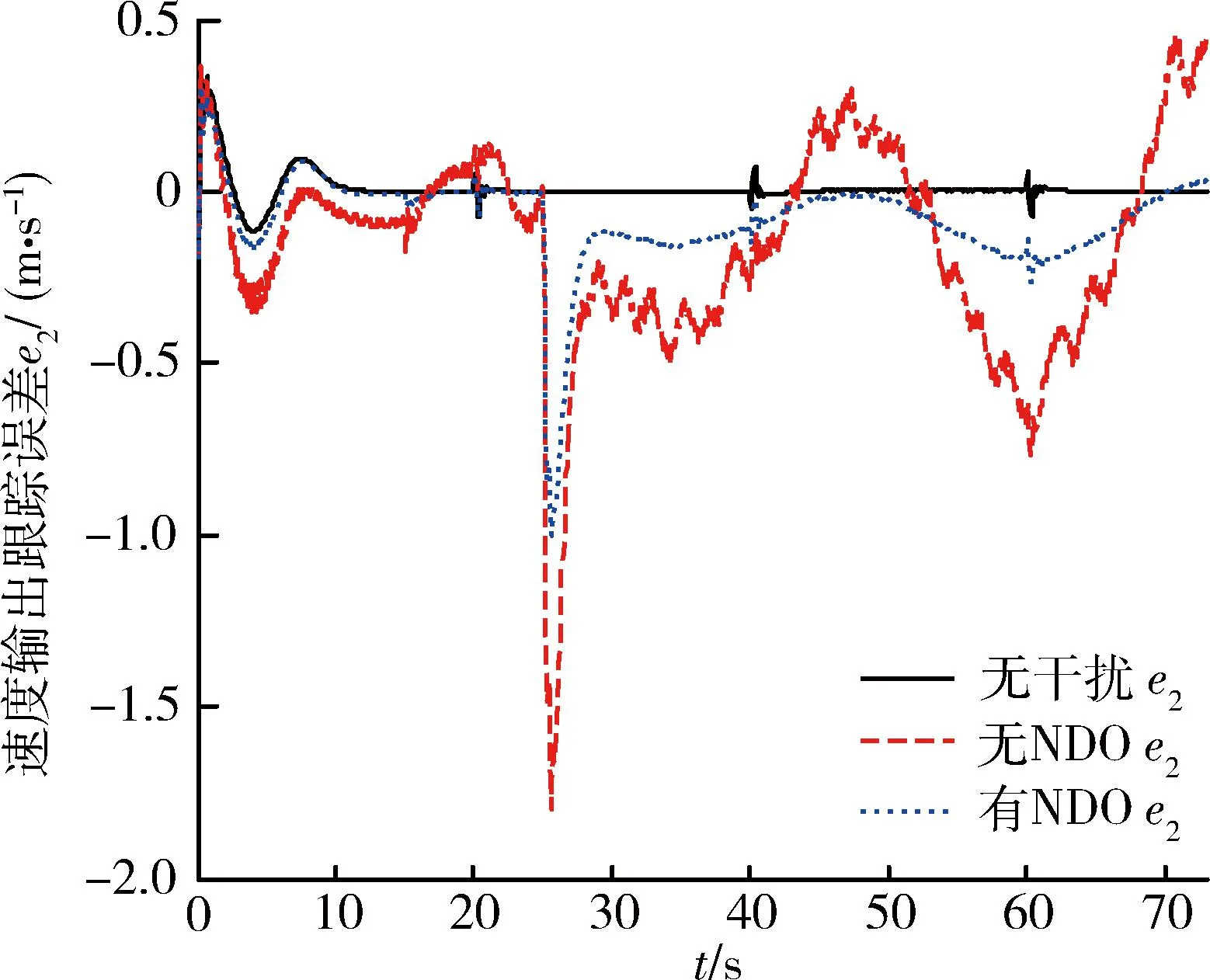
图4　输入舵偏角变化曲线Fig.4　Response of rudder deflection angle

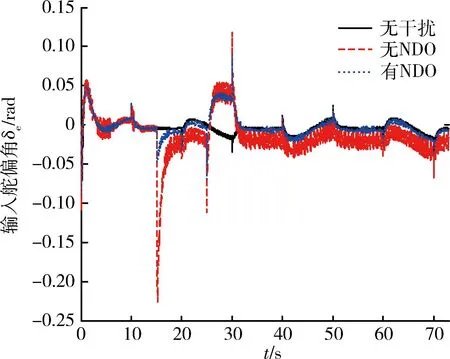
图5　油门开度变化曲线Fig.5　Response of accelerator opening

图6　攻角变化曲线Fig.6　Response of attack angle

图7　俯仰角速率变化曲线Fig.7　Response of pitch angle rate

图8　虚拟控制量变化曲线Fig.8　Response of virtual control volume

图9　虚拟控制量变化曲线Fig.9　Response of virtual control volume

图10　外界干扰d3观测值及其实际值Fig.10　Observing and real value of disturbance d3

计的非线性滑模观测器能够快速准确地观测出外加干扰。

图11　外界干扰d8观测值及其实际值Fig.11　Observing and real value of disturbance d8

4结束语

本文在对高超声速飞行器纵向运动模型分析的基础上，设计了非线性干扰观测器对系统干扰进行观测。然后，基于反馈线性化和反演控制设计方法设计了反演多滑模控制器，实现对参考指令的跟踪控制。仿真结果表明，设计的非线性干扰观测器能够准确观测系统干扰，有效削弱控制输入引起的抖振。该控制器对系统中的匹配和非匹配不确定性均具有较好的鲁棒性，具有良好的跟踪控制性能。

参考文献：

[1]宋超，赵国荣，盖俊峰.基于非线性干扰观测器的高超声速飞行器反演滑模控制[J].系统工程与电子技术，2012，34(6)：1231-1234.

SONG Chao, ZHAO Guo-rong, GAI Jun-feng. Sliding Mode Backstepping Control for Hypersonic Aircraft Based on Nonlinear Disturbance Observer [J].Systems Engineering and Electronic，2012，34(6)： 1231-1234．

[2]张元涛，石为人，邱明伯.一类不确定非线性系统的参数化自适应滑模控制[J].华中科技大学学报：自然科学版，2011，39(5)：79-82.

ZHANG Yuan-tao, SHI Wei-ren, QIU Ming-bo. Parameter Adaptive Sliding Mode Control for a Class of Uncertain Nonlinear Systems [J].J.Huazhong Univ. of Sci. & Tech:Natural Science ed.，2011, 39(5):79-82.

[3]王坚浩，胡剑波.一类非匹配不确定非线性系统的鲁棒跟踪控制[J].控制与决策，2011，26(5)：727-731.

WANG Jian-hao, HU Jian-bo. Robust Racking Control for a Class of Nonlinear Systems with Unmatched Uncertainties [J].Control and Decision, 2011, 26(5):727-731.

[4]XU H J，MIRMIRANI M D，LOANNOU P A. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J].Journal of Guidance，Control and Dynamics，2004，27(5)：829-837.

[5]MCDUFFIE Y，Yuri Shtessel.Sliding Mode Control of the X-33 Vehicle in Launch and Reentry modes[C]∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Denver：AIAA，2000-4158.

[6]宋超，赵国荣，陈洁.基于鲁棒滑模观测器的高超声速飞行器双环滑模控制[J].固体火箭技术，2012，35(4)：438-441.

SONG Chao,ZHAO Guo-rong,CHEN Jie. Dual-Loop Sliding Mode Control for Hypersonic Aircraft with Robust Sliding Mode Observer [J].Journal of Solid Rocket Technology, 2012, 35(4):438-441.

[7]高为炳.变结构控制理论及设计方法[M].北京：科学出版社，1996.

GAO Wei-bing. Theory and Design Method for Variable Structure Control [M].Beijing: Science Press, 1996.

[8]时建明，王洁，叶继坤，等.吸气式高超声速飞行器输入受限自适应反演控制[J].固体火箭技术，2012，35(5)：573-577.

SHI Jian-ming, WANG Jie, YE Ji-kun, et al. Adaptive Backstepping Control for an Air-Breathing Hypersonic Vehicle with Input Constraints [J].Journal of Solid Rocket Technology, 2012, 35(5):573-577.

[9]TAEYOUNG L，YOUDAN K. Nonlinear Adaptive Flight Control Using Back-Stepping and Neural Networks Controller [J]. Journal of Guidance，Control and Dynamics，2001，24(4)：675-682.

[10]LI Y H，QIANG S，ZHUANG X Y，et al. Robust and Adaptive Back-Stepping Control for Nonlinear System Using RBF Neural Networks [J]. IEEE Transactions on Neural Networks，2004，15(3)：693-701.

[11]刘金琨.滑模变结构控制MARLAB仿真[M].北京：清华大学出版社，2012.

LIU Jin-kun. MATLAB Simulation for Sliding Mode Control [M].Beijing: Tsinghua University Press, 2005.

[12]时建明，王洁，王琨，等.吸气式高超声速飞行器纵向运动反演控制器设计[J].西安交通大学学报，2013，47(3)：102-107.

SHI Jian-ming,WANG Jie,WANG Kun,et al. Design of Backstepping Controller for Longitudinal Motion of an Air-Breathing Hypersonic Vehicle[J].Journal of Xi’an Jiaotong University,2013,47(3):102-107.

[13]CHEN W H. Nonlinear Disturbance Observer-Enhanced Dynamic Inversion Control of Missile [J].Journal of Guidance，Control and Dynamics，2003，26(1)：161-166.

[14]CAI Guang-bin，DUAN Guang-ren，HU Chang-hua. On Some Classes of Control-Oriented Model of Air-Breathing Hypersonic Vehicles[C]∥2010 Chinese Control and Decision Conference，CHN：IEEE，2010：2955-2959.

[15]李惠峰.高超声速飞行器制导与控制技术[M].北京：中国宇航出版社，2012.

LI Hui-feng. Guidance and Control Technology of Hypersonic Vehicle [M].Beijing: China Aerospace Press, 2012.

[16]瞿章华，刘伟，曾明，等.高超声速空气动力学[M].长沙：国防科技出版社，2001.

QU Zhang-hua， LIU Wei， ZENG Ming，et al. Hypersonic Aerodynamics [M]. Changsha: National University of Defense Technology Press，2011.

[17]乔继红.反演控制方法与实现[M].北京：机械工业出版社，2011.

QIAO Ji-hong. Back-Stepping Control Theory and Realize [M]. Beijing：China Machine Press，2011.

Backstepping Multi-Sliding Mode Control for Hypersonic Vehicle Based on Nonlinear Disturbance Observer

TANG Yi-dong，LI Xiao-bing，LEI Hu-min

(AFEU，Air and Missile Defense School，Shaanxi Xi’ an 710051，China)

Abstract:For the matching and mismatched uncertainties control problem ofhypersonic vehicle, depending on nonlinear disturbance observer (NDO), a flight multi-sliding mode controller for the triangular standard form of longitudinal motion model isdesigned based on backstepping and sliding mode control scheme. The NDO is used to observe the disturbance of system. The sliding mode control is ledin each step of backstepping process for controller designing. Simulation results show that the NDO can observe the disturbance accurately, and the controller makes sure of the stability and robust of system.

Key words:hypersonic;nonlinear disturbance observer(NDO); uncertainty; backstepping control; sliding model control

中图分类号：V448

文献标志码：A

文章编号：1009-086X(2015)-02-0054-08

doi:10.3969/j.issn.1009-086x.2015.02.010

通信地址：710051陕西省西安市长乐东路甲字一号空军工程大学防空反导学院研2队E-mail：510447289@qq.com

作者简介：唐意东(1989-)，男，四川富顺人。硕士生，研究方向为飞行器控制。

* 收稿日期：2014-05-03；
修回日期：2014-07-23