单向微波加热木材内温度模型的热源反演数值方法1)

吴晓婷 王行建 张春蕊

(东北林业大学，哈尔滨，150040)

责任编辑:戴芳天。

木材加工处理过程中存在大量的传热过程，同时热传递过程是研究该过程材料变化机理的一个重要切入点。近年来，随着工艺技术水平的不断提高和加热新方法的不断推出，微波加热处理等方法更为广泛地被使用，对其研究的内容也更加深入。木材微波处理过程中，微波能量以电磁波的形式直接穿透到木材内部，并通过微波电磁场与木材中水分子和其他极性基团的相互作用而迅速产生大量的热，实现木材的快速干燥和改性预处理［1］。对于微波干燥或预处理过程中木材内部的温度分布，学者曾提出不同的看法。文献［2］中提到在微波干燥过程中，木材内存在着内高外低的温度场，并认为该温度场的存在是使木材具有高干燥速率的主要原因。文献［3］认为在一定的辐射功率和厚度范围内，木材厚度方向温度分布比较均匀，基本不呈现出内高外低或外低内高的温度梯度。李贤军等人从热传导的物理规律出发，建立了微波加热过程中木材内部的热传导模型，并且说明了不同微波加热方式对木材内部温度分布有不同影响。该模型的热传导方程中包含热源项，通常热源的解析解是不容易得到的。文献［4］运用分离变量法，边界条件齐次化，定义算子等相结合的方法求解了微波加热过程中木材内部的热传导模型中热源的近似解析解。文献［5］讨论的是非线性热传导方程中未知系数反演，运用中心差分离散方程得到迭代矩阵;然后通过建立牛顿迭代公式求解迭代增量，进而反演出方程中未知系数。

笔者借鉴文献［3］的方法来讨论微波加热过程中木材内部热传导模型中热源的数值解，最终得到了求解这一类热传导方程反问题的稳定的数值解法。微波加热过程中木材内部温度分布随时间变化的模型即为形如模型(1)［5］的热传导方程:

式中:U 指温度值，未知的非齐次项Φ 即称为热源，求解热源Φ 的过程即为热源反演过程。

1 热传导方程的反演

1.1 模型离散

对模型(1)进行离散，采用均匀的网格剖分如下:

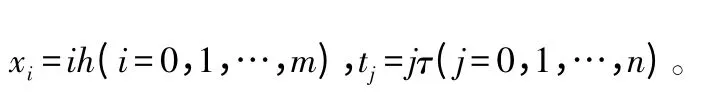
对方程，在(xi，tj+1/2)处采用中心差分离散:

有简记形式如下:

则得到:

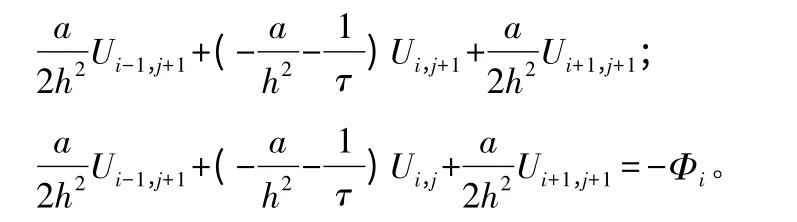
在x=0，x=l 处离散边界条件得到:

当把离散格式写成矩阵方程组的形式，则可以得到迭代矩阵:

式中:Qj+1是(m+1)×(m+1)阶严格三对角占优阵;Wj+1是三对角矩阵，且有:

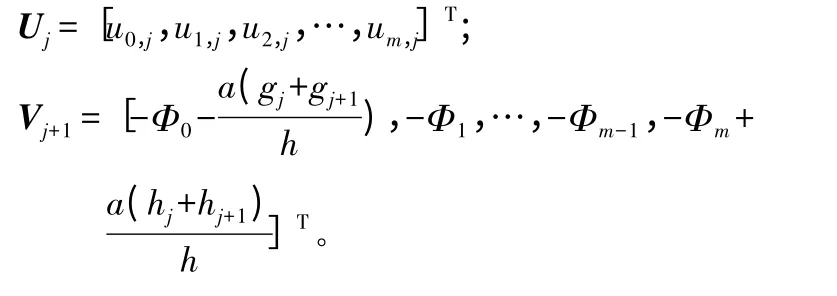
由此可得到迭代矩阵，并且可通过证明得到此格式稳定，并且对于输入条件的扰动也是稳定的。

1.2 迭代增量及牛顿迭代格式

首先选择误差函数为:

选择热源函数类为:

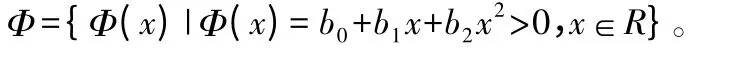
为了使T 最小，只需要令T 关于b0，b1，b2的偏导数均为零，即

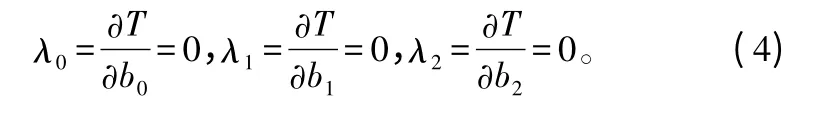
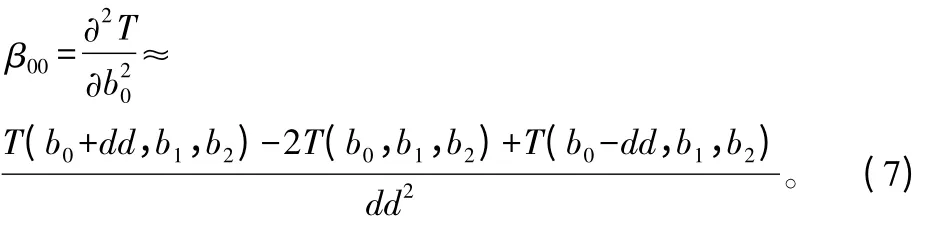
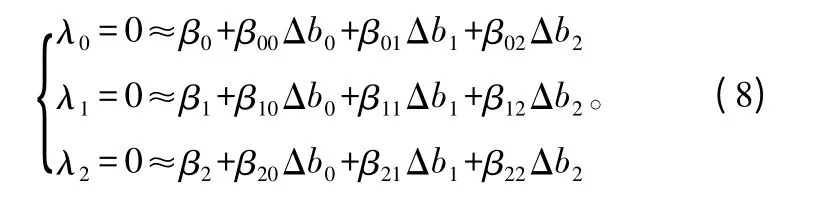
式中:Δb0，Δb1，Δb2分别为b0，b1，b2的迭代改善增量;dd 是偏导数的离散步长，关于b0，b1，b2采用相同的离散步长。

2 单向微波处理中木材内部温度分布模型的热源数值反演

单向微波加热时，微波加热过程中木材内部温度分布随时间变化的热传导模型如下:

式中:q0，λ，c，b 分别表示微波辐射功率、木材传热系数、热容量、木材对微波的吸收系数，其取值由文献［3］中的值确定，分别为:

即热源函数系数的精确解为:

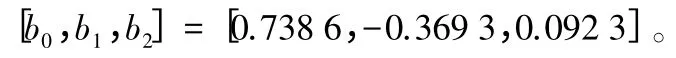
基于第一部分的方法，对模型(2)中的热源进行数值反演。在这里将热源函数的系数初值选为:

在空间和时间上采用相同的m=n 等分的网格剖分，表1为取不同网格剖分时的计算结果。

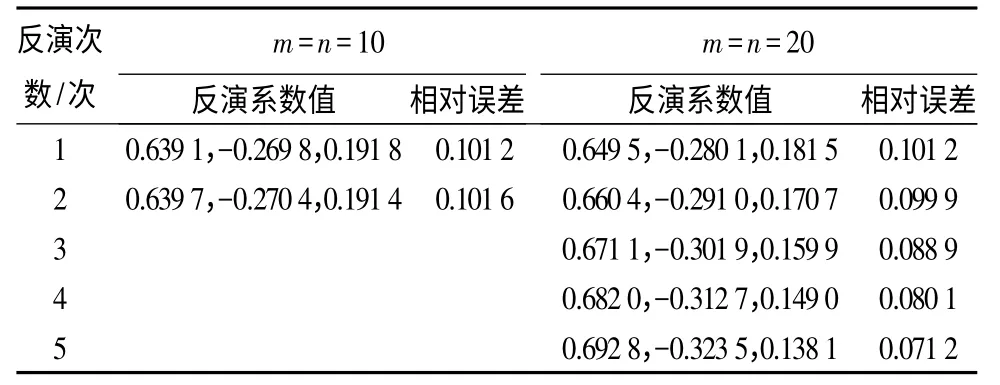
表1 不同网格剖分时的计算结果

当m=n=20 选取时，第5 次反演得到的近似热源函数为:

图1为当m=n=20 时，热源实际值与选取的热源初值反演得到的热源值的对比图像。图1和表1显示了经过反演后的热源值更接近于实际值，反演次数越多，反演值越接近实际值;而且网格剖分越细，反演效果越好，反演值越接近实际值。

图1 热源实际值与反演值对比图

3 结论

研究了单项微波辐射时，微波加热过程中木材内部温度随时间变化的热传导模型的热源反演。对于这一类热传导模型，采用的方法是，首先用有限差分法将偏微分方程及其初边值条件离散，得到迭代方程，用来求解网格节点上的温度值;经过相应的理论推导可得到此迭代方程是稳定且收敛的。然后，运用最小二乘法构造误差函数，对误差函数的一阶偏导数进行一阶泰勒展开，令一阶偏导数为零，近似得到计算热源的牛顿迭代格式。最后进行反演，并将反演结果与实际值作比较，模拟结果表明该方法有很好的逼近效果，于是得到了求解这一类热传导方程反问题的稳定的数值解法。

［1］ 李贤军，孙伟胜，周涛，等.微波处理中木材内温度分布的数学模拟［J］.林业科学，2012，48(3):117－121.

［2］ 佟永会.木材微波干燥工艺的研究［J］.东北林业大学学报，1986，14(3):67－73.

［3］ 李贤军，张璧光，李文军，等.微波真空干燥过程中木材内部的温度分布［J］.北京林业大学学报，2006，28(6):128－131.

［4］ 刘畅，王行建，曹军.微波处理中木材内温度分布模型的热源反演［J］.东北林业大学学，2014，42(8):131－132.

［5］ 赵丽玲.一类非线性热传导方程的反演计算［D］.杭州:杭州师范大学，2013.