AHP-TOPSIS评判模型在采矿方法转换中的应用
秦健春 李业辉 文留海
(柳州华锡有色设计研究院有限责任公司)
·采矿工程·
AHP-TOPSIS评判模型在采矿方法转换中的应用
秦健春 李业辉 文留海
(柳州华锡有色设计研究院有限责任公司)
铜坑矿92#矿体随着采矿生产的不断深入,地压活动进一步加剧,使空区周边采场出现应力集中,引起岩层开裂、破碎、沉降等现象,致使开采技术条件变差,采矿损失贫化逐渐加大,矿山经济效益严重下降,必须将在用的崩落采矿法进行转换。利用层次分析法与逼近理想解排序法构建AHP-TOPSIS评判模型,计算出4种备选采矿方法的综合优越度分别为61%,30.87%,53.91%,34.62%,从而确定机械化上向水平分层充填法最优。实践表明:AHP-TOPSIS评判模型在采矿方法优化选择中具有工程的可比性和实用性。
采矿方法转换 层次分析法 逼近理想解排序法 评判指标 综合评判模型
采矿方法作为矿山生产中的重要组成部分,涉及到众多矿山生产的技术经济指标。采矿方法的选择合理与否,将直接关系到矿山的生产安全和经济效益。由于采矿方法转换涉及着矿山生产的诸多方面,因此,不到迫不得已,矿山不会转换采矿方法。
铜坑矿92#矿体走向近东西,倾向北,向北东方向侧伏,呈南高北低、西高东低展布;矿体倾角为15°~25°,矿体厚度变化系数为86.27%,品位变化系数为215%,呈缓倾斜似层状产出,属于缓倾斜厚至极厚复杂难采矿体。自2001年起,92#矿体采用崩落法开采,随着采矿生产往深部延伸,由采矿引起的地压灾害、地表塌陷、采矿损失贫化高以及三级矿量不足等问题日趋严重,生产组织愈加困难,经济效益严重下降,为解决这些问题,矿山拟对在用的崩落采矿法进行转换。
以往的采矿方法优化选择仅是直观地评判而确定的,易受到经验和主观因素影响而不能正确反映真实情况[1-2]。目前,在采矿方法优化选择中不确定性分析方法得到了广泛的应用,国内外研究较多的包括有模糊数学理论方法[3]、灰色优化理论、层次分析法[4]、突变级数法(CPM)[5]以及BP神经网络分析法[6]等,虽然这些方法在采矿方法优化选择中起到一定作用,但是仍存在诸多不足之处[7-8]。因此,本文采用层次分析法和逼近理想解排序法[9-10],构建AHP-TOPSIS评判模型,对采矿方法优化选择,计算方案综合优越度,确定最优采矿方法。
1 权重确定
基于递阶层次综合评判指标结构体系,利用层次分析法对方案决策中各影响指标的权重系数进行合理分配。
1.1 对比标度
参照对比的标度与判断分析,可利用模糊数学方法获得以下两两对比标准[11],见表1。
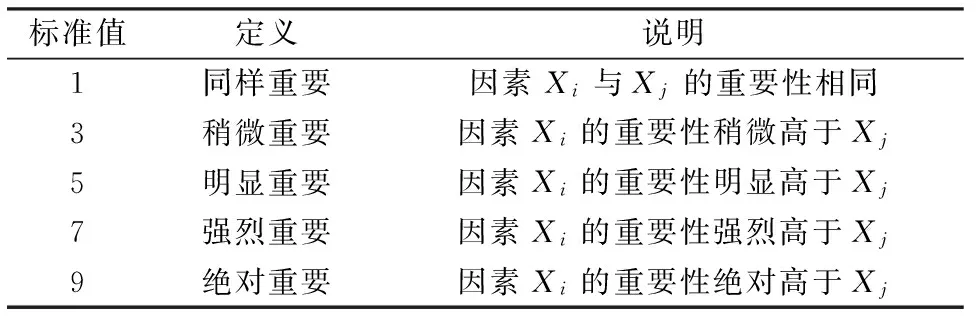
表1 对比标准意义
注:①2,4,6,8分别表示上述两相邻标准值判断的中值;②Xi与Xj对比得Wij,则Xj与Xi对比得1/Wij。
1.2 判断矩阵
根据上述两两对比标度方法构建对比判断矩阵,设判断矩阵D为
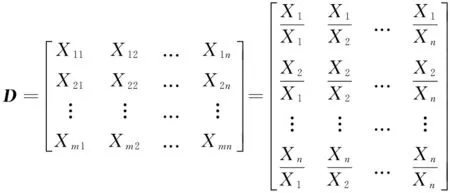
对于两两对比标度方法构建的判断矩阵,解特征根问题,所得到的W经正规化后当作影响指标的权重系数。
(1)判断矩阵D内各元素以行行相乘,获得各行元素乘积Mi:
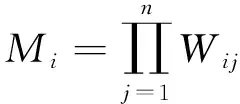
(1)
(2)Mi的n次方根:
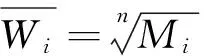
(2)
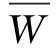
(3)
(4)判断矩阵D最大特征根:
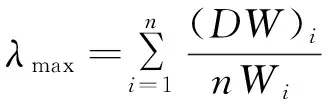
(4)
1.3 一致性检验
为确保判断结果能与实际情况相符,对判断矩阵进行一致性检验。一致性检验公式为
(5)
(6)
式中,CI为一致性检验指标;RI为平均随机一致性指标,n为判断矩阵阶数;RI取值见表2。
当CR<0.1时,判断矩阵D通过一致性检验,反之则须调整判断矩阵,直至通过一致性检验。
1.4 权重计算
判断矩阵D通过一致性检验,即可计算出各影响因素的权重系数。
2 AHP-TOPSIS评判模型构建
2.1 初始评判矩阵
设有A1,A2,…,Am共m个对比方案组成方案集A={A1,A2,…,Am},每个方案的评判指标X1,X2,…,Xn组成评判指标集X={X1,X2,…,Xn},评判指标记为Xij(i=1,2,…,m;j=1,2,…,n),Xij代表第i个方案第j个评判指标,可构建初始评判矩阵A:
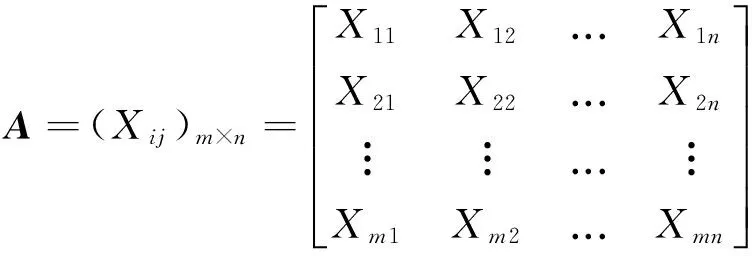
2.2 标准化决策矩阵
由于评判指标具有不同的量纲和单位,为消除其不可公度性,对评判指标值无量纲化[12]。标准化决策矩阵B=(bij)m×n的计算如下:
(1)越大越优指标为
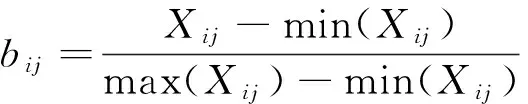
(7)
(2)越小越优指标为
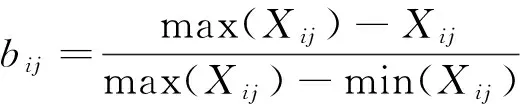
(8)
2.3 加权标准化决策矩阵
标准化决策矩阵B中各列元素与利用层次分析法计算的各指标权重wn相乘,可建立加权标准化决策矩阵C:

2.4 评判对象贴近度
(1)理想解确定:
(9)
式中,C+和C-为正理想解与负理想解;J1和J2为效益型指标集与成本型指标集。
(2)评判对象与理想解距离计算:
(10)
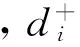
(3)评判对象与正理想解贴近度计算:
(11)
(4)评判对象综合评判:
F=W×E,
(12)
式中,E为由各评判对象与正理想解贴近度建立的评判矩阵;W为利用层次分析法计算的各方案权重系数;F为评判结果向量。
3 实例应用
3.1 评判指标体系
采矿方法评判是一个复杂工程,在评判指标体系中,存有定量参数和定性参数,因此在评判指标选取时,以尽可能少的评判指标来呈现最重要、最全面的信息[13]。按照层次分析法理论,构建采矿方案综合评判指标体系目标层O,其包含3个准则层,分别为经济指标层(P1),包括采充综合成本(X1)、矿石回采率(X2)、矿石贫化率(X3);技术指标层(P2),包括千吨采切比(X4)、方案灵活适应性(X5)、实施难易程度(X6)、采场生产能力(X7);安全指标层(P3),包括地压控制效果(X8)、通风条件(X9)及爆破对采场稳定性的影响程度(X10)。在评判过程中,可按照矿山实际状况对上述指标进行增减。
根据92#矿体开采技术条件以及井下生产状况,可确定4种备选采矿方法,分别为机械化上向水平分层充填法(方案Ⅰ)、分段凿岩阶段出矿嗣后充填法(方案Ⅱ)、机械化上向水平进路充填法(方案Ⅲ)、分段空场嗣后充填法(方案Ⅳ)。为更直观体现评判指标体系,构建评判指标层次框架分析图,见图1。对4个备选方案进行评判,构建的评判指标体系及相应指标值,见表3。
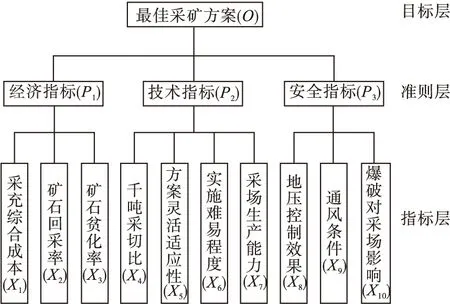
图1 指标层次框架

表3 各方案的综合评判指标体系
3.2 评判指标权重确定
按照层次分析法理论,通过查阅国内外相关文献,并与现场人员、相关专家商讨,从而建立目标层对应于准则层的O-P判断矩阵,见表4。
根据已确定的评判指标权重,可计算特征值λmax0=3.05,CI0=0.05,RI0=0.58,CR0=0.043<0.1,该判断矩阵通过一致性检验,即权重系数W=[0.474,0.376,0.150]可接受。
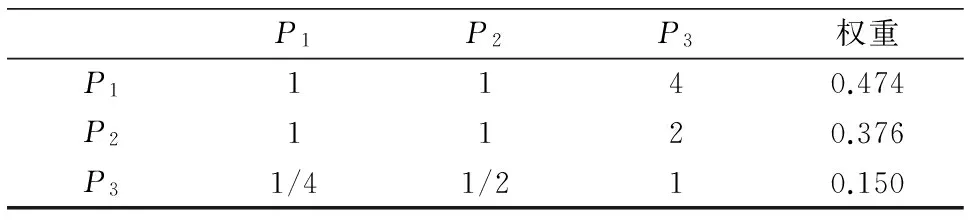
表4 O-P判断矩阵
同理可计算P1-P1j,P2-P2j,P3-P3j各二级评判指标权重。
P1-P1j:w1=[0.4,0.2,0.2],λmax1=3,CI1=0,RI1=0.58,CR1=0<0.1;
P2-P2j:w2=[0.441,0.311,0.124,0.124],λmax2=4.062,CI2=0.021,RI2=0.90,CR2=0.023<0.1;
P3-P3j:w3=[0.493,0.311,0.196],λmax3=3.054,CI3=0.027,RI3=0.58,CR3=0.047<0.1。
评判指标层次总排序,见表5。
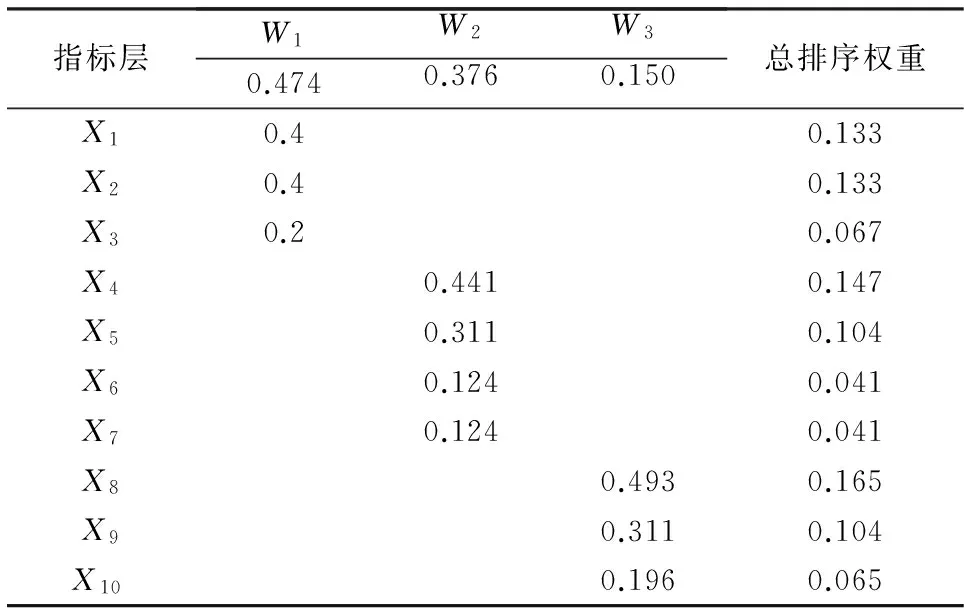
表5 评判指标层次总排序表
3.3 指标评判
3.3.1 经济指标评判
(1)建立经济指标初始评判矩阵:

(2)计算加权标准化决策矩阵:
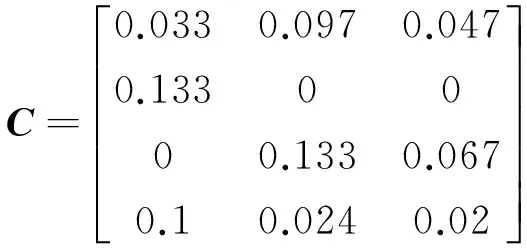
(3)按照式(9)~式(11)计算基于经济指标的各方案贴近度:
于经济指标层面,成本型指标包括采充总成本与矿石贫化率;效益型指标包括矿石回收率,则正理想解与负理想解为

各备选方案同正理想解、负理想解的距离为
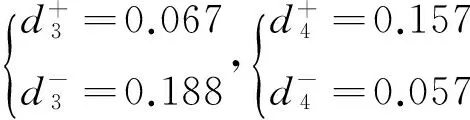
各备选方案和正理想解的贴近度为

由上可知,于经济指标层,方案Ⅲ最优,其次为方案Ⅰ。
3.3.2 技术指标评判
(1)与经济指标评判过程相同,可建立技术指标层加权标准化决策矩阵:

(2)于技术指标层面,成本型指标包括采切比与实施难易程度;效益型指标包括方案灵活适应性与采场生产能力,则正理想解与负理想解为
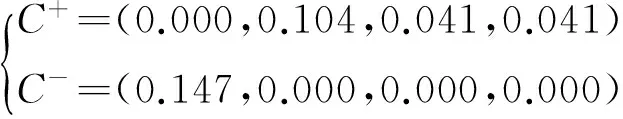
各备选方案同正理想解、负理想解的距离为
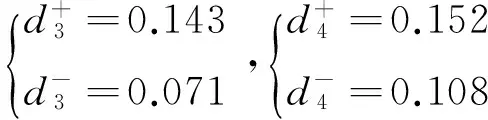
各备选方案和正理想解的贴近度为

由上可知,于技术指标层,方案Ⅰ最优,其次为方案Ⅳ。
3.3.3 安全指标评判
(1)与上述指标评判过程相同,可建立安全指标层加权标准化决策矩阵:

(2)于安全指标层面,成本型指标包括爆破对采空区周边稳定性的影响程度;效益型指标包括空区最大暴露面积与通风条件,则正理想解、负理想解为

各备选方案同正理想解、负理想解的距离为
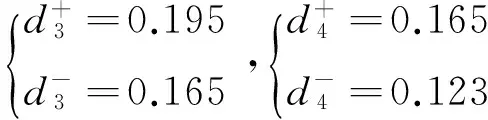
各备选方案和正理想解的贴近度为
由上可知,于安全指标层,方案Ⅰ最优,其次为方案Ⅲ。
3.4 采矿方法综合评判
利用层次分析法原理计算出准则层各指标权重系数为W=[0.474,0.376,0.150],各评判指标的贴近度建立评判矩阵为

按照式(12)计算得
F=W×E=(0.61,0.3087,0.5391,0.3462) .
综上可得各采矿方案的综合优越度:方案Ⅰ,61%;方案Ⅱ,30.87%;方案Ⅲ,53.91%;方案Ⅳ,34.62%。方案优劣次序为Ⅰ>Ⅲ>Ⅳ>Ⅱ,从而最终确定方案Ⅰ,即机械化上向水平分层充填法最优。
4 结 语
(1)按照层次分析法理论构建评判指标体系,从经济、技术和安全3个层面确定了影响评判的10个指标,计算出各层次评判指标的权重系数,避免了对评判指标权重、评判结果的人为主观影响。
(2)结合层次分析法与逼近理想解排序法构建AHP-TOPSIS评判模型,计算得出4个备选方案的综合优越度依次为61%,30.87%,53.91%,34.62%,确定机械化上向水平分层充填法最优。
(3)经矿山生产实践证明,运用AHP-TOPSIS评判模型确定的采矿方法在经济、技术、安全方面是合理可行的,实现了铜坑矿92#矿体安全、高效、低成本开采。AHP-TOPSIS评判模型能有效解决采矿方法选择过程中由于影响因素太多而难以分配权重的难题,也能避免单因素决策的片面性以及人为主观因素所导致的决策错误。
[1] 颜春萍.人机系统价值的模糊综合评价[J].湖南科技大学学报:自然科学版,2007,22(1):78-80.
[2] 鲁光银,韩旭里,朱自强,等.地质灾害综合评估与区域模型[J].中南大学学报:自然科学版,2005,36(5):877-881.
[3] Li L, Li Y M. The design and stability analysis of adaptive system based on linear T-S fuzzy system[J]. Acta Automatica Sinica, 2003, 29(6): 1024-1026.
[4] 王新民,赵彬,张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报:自然科学版,2008,39(5): 875-880.
[5] 谷新建,柴红保.应用突变评价理论选择采矿方法[J].中国安全科学学报,2004,7(7):13-15.
[6] Wang W Y, Leu Y G, Lea T T. Robust adaptive fuzzy-neural control of nonlinear dynamical systems using generalized projection update law and variable structure controller[J].IEEE Trans Syst Man Cybern, Part B: Cybernetics, 2001, 30(1):140-147.
[7] 宫凤强,李夕兵,高科.地下工程围岩稳定性分类的突变级数法研究[J].中南大学学报:自然科学版,2008,39 (5):1081-1086.
[8] 于德海,彭建兵.地下工程围岩分类的神经网络可视化评价[J].中围地质灾害与防治学报,2005,16(4):116-119.
[9] LIN Mingchyuan,WANG Chencheng, CHEN Mingshi, et al. Using AHP and TOPSIS approaches in customer-driven product design process[J].Computers in Industry, 2008(59):17-31.
[10] Dagdeviren M. Weapon selection using the AHP and TOPSIS methods under fuzzy environment[J].Expert Systems with Applica-tions,2009(36):8143-8151.
[11] 黄贯虹,方刚.系统工程方法与应用[M].广州:暨南大学出版社,2005.
[12] 谢本贤,陈沅江,史秀志.深部岩体工程围岩质量评价的IRMR法研究[J].中南大学学报:自然科学版, 2007,38(5): 987-992.
[13] 李俊芳,吴小萍.基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J].武汉理工大学学报,2007,4(2):205-208.
Application of AHP-TOPSIS Evaluation Model in Mining Method Conversion
Qin Jianchun Li Yehui Wen Liuhai
(Liuzhou Huaxi Non-ferrous Design Research Institute Co., Ltd.)
With the deeply mining, the ground pressure activities of 92#orebody of Copper pit mine intensify further, the stress concentration phenomenon appeared around the mined-out area, and the phenomenona of rock cracking, crushing and sedimentation are caused. So the mining technical conditions become poor, loss of mining dilution increases gradually, it is necessary to conduct conversion of the existing caving mining method. The AHP-TOPSIS evaluation model is established based on analytic hierarchy process method and the sorting method of approximation to the ideal solution so as to calculate the comprehensive superiority degree values of four alternative mining methods. The results are 61%, 30.87%, 53.91%, 34.62%. So the mechanization upward horizontal slice stoping and backfilling method can be regarded as the best one. The research results of this paper show that the AHP-TOPSIS evaluation model is suitable for optimal selecting of mining method.
Mining method conversion, Analytic hierarchy process method, Sorting method of approximation to the ideal solution, Evaluation indicator, Comprehensive evaluation model
2014-10-16)
秦健春(1988—),男,硕士研究生,545005 广西壮族自治区柳州市。

