点估计方法在功能函数有折点时的适用性

梁 子 杨

(华北水利水电大学土木与交通学院，河南 郑州 450045)



点估计方法在功能函数有折点时的适用性

梁 子 杨

(华北水利水电大学土木与交通学院，河南 郑州 450045)

通过实例计算比较点估计方法和蒙特卡洛模拟的结果，功能函数有折点时，点估计方法的精度并非随估计点数增加而单调增加，当估计点个数足够多时，点估计方法计算结果稳定，且有较好的精度。在同等精度要求下，功能函数有折点时点估计方法计算量与功能函数光滑时相比有所增加，但与蒙特卡洛模拟相比，仍有较高的计算效率。

点估计方法，结构功能函数，蒙特卡洛模拟，计算效率

可靠度理论基本的问题是求解结构失效概率，其求解需要通过简化计算。传统的一次二阶矩、二次二阶矩等方法已被指出精度不高。蒙特卡洛模拟可达到很高的精度，但计算量很大。

Zhao提出的矩法，通过点估计方法得到结构功能函数的前四阶矩，进而求解失效概率。功能函数为光滑曲线时，文献表明，进行5点或7点估计，就有较高的精度，且精度随着估计点数的增加单调增加。弹塑性分析时，功能函数会有折点，此时点估计方法的适用性尚需研究。

1 点估计方法

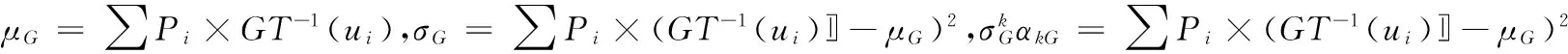
2 功能函数有折点情况

在弹塑性分析时，通常在结构易屈服处设置塑性铰。塑性铰骨架曲线通常简化为多折线形式。例如，对于一个单跨刚架进行静力弹塑性分析，有两个柱为构件1和构件3，一个梁为构件2，其中构件1截面EI1=1.675×107N·m2，构件2和3截面EI2=3.35×107N·m2。分别在构件1，3与地面固结处设置塑性铰，塑性铰骨架曲线M—θ采用双折线形式。构件1屈服弯矩My=8 000 kN·m，屈服转角θy=0.001 rad，极限转角θu=0.03 rad。构件2屈服弯矩My=10 000 kN·m，屈服转角θy=0.002 rad，极限转角θu=0.06 rad。

假定在梁构件2与柱构件1节点处施加一水平荷载P～N(3.5,0.1)，构件1底部截面转角达到0.001 5 rad时，刚架失效。刚架功能函数可表示为：Z=G(P)=θR-θS，θR为构件1底部截面的能力，θR=0.001 5 rad,θS为构件1底部截面的转角反应。

计算得到Z=G(P)函数有两个折点。构件1底部截面首先进入塑性，功能函数出现第一个折点，坐标为(3.351 7,0.000 5)；构件2底部截面随荷载的增大进入塑性，功能函数出现第二个折点，坐标为(3.561 7,0.000 3)。

3 算例与分析

计算2个有折点的功能函数算例，并与蒙特卡洛模拟结果比较。

3.1 算例1

构造有一个折点的功能函数：x<-1时Z=G(x)=-0.5x+0.5，x≥-1时Z=-x；假定x～N(0，1)。

蒙特卡洛模拟样本足够多时，认为是准确值，点估计方法与蒙特卡洛模拟结果的相对误差如图1所示。可得点估计方法的计算误差在准确值附近震荡，当估计点达到一定数目后，误差稳定。要保证计算误差小于5%，算例1中点估计方法需要15点估计。

蒙特卡洛模拟计算失效概率一般需要样本数N=100/Pf。算例1失效概率为0.500 3，蒙特卡洛模拟至少需要计算200次。点估计方法要计算的次数是前15次相加为63次，是蒙特卡洛模拟计算次数的1/3。

3.2 算例2

构造有两个折点的功能函数：x<0时，Z=G(x)=-0.75x+3.25,0≤x<1时Z=-x+3，x≥1时Z=-1.33x+3.33；假定x～N(0.1)。

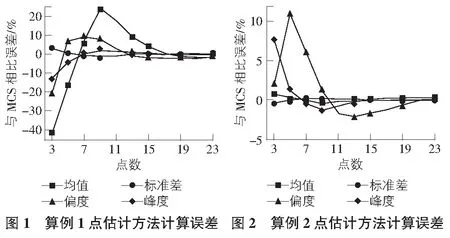
点估计方法与蒙特卡洛模拟结果的相对误差如图2所示。得到与算例1相同的结论，要保证计算误差小于5%，则算例2中点估计方法需要9点估计。

对于此算例，失效概率为0.006 21，蒙特卡洛模拟至少需要计算1.6×104次。点估计方法需要计算的次数为24次，仅为蒙特卡洛模拟计算次数的1/667。

4 结语

1)功能函数有折点时，点估计方法的精度并非随估计点数增加而单调增加，当估计点个数足够多时，其计算结果基本稳定，且有较好的精度。2)精度达到一般工程精度要求的5%时，功能函数有折点时的点估计方法计算量比功能函数光滑时的计算量多，对于本文的两个算例，前者是后者的5倍～12倍。3)精度达到一般要求的5%时，对于本文的两个算例，蒙特卡洛模拟计算量是点估计方法计算量的3倍～700倍，且失效概率越小，蒙特卡洛模拟法的计算量越大，点估计方法相对于蒙特卡洛模拟的计算效率越高。

[1]张 明.结构可靠度分析——方法与程序.北京：科学出版社，2009.

[2]Zhao YG. New point-estimates for probability moments.Engrg,Mech,ASCE，2000,126(4):433.

The applicability of point estimation method in function with salient point

Liang Ziyang

(CivilEngineeringandTransportationCollege,NorthChinaWaterConservancyandHydropowerUniversity,Zhengzhou450045,China)

Through the example calculation comparison of point estimation method and Monte Carlo simulation results, when the function with salient point, the accuracy of point estimation method monotonically increased with the increasing of estimation numbers, when the estimation numbers large enough, the point estimate method results were stable, and had good accuracy, at the same accuracy requirements, compared with function with smooth the point estimation methods calculation quantity of function with salient point increased, but compared with Monte Carlo simulation, still had higher computational efficiency.

point estimation method, structure function, Monte Carlo simulation, computational efficiency

1009-6825(2015)18-0045-02

2015-04-12

梁子杨(1994- )，女，在读本科生

U441.3

A