GPS信号捕获策略的研究

陶 帅， 孙克文

（合肥工业大学 计算机与信息学院，安徽 合肥 230009）

在GPS接收机中，最耗时的操作就是GPS信号的捕获，捕获的目的是找到可视卫星，并对其信号的C／A码相位以及多普勒频移进行估计。为了估计某个卫星信号的载波频率和码相位，接收机的信号捕获过程一般是通过对该卫星的载波频率和码相位这二维进行扫描式搜索来完成的。一旦信号被搜索到并得以确认，那么对该信号的捕获过程也就结束。

GPS卫星所发射的L1载波信号的中心频率为1 575.42MHz，但是由于卫星与用户接收机在两者连线方向上的相对运动所引起的多普勒效应、接收机晶体振荡频率漂移等因素的影响，接收机实际接收到的卫星载波信号的中心频率一般不再等于L1标称频率；同时由于卫星到接收机的距离时刻在发生变化，加上接收机时钟相对于GPS时间的偏差并不固定，因此接收信号的码相位值也在时刻变化，所以需要对多普勒频移和码相位进行二维搜索。

1 GPS信号模型

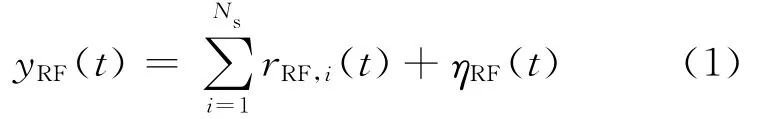
在加性高斯噪声环境下，GPS接收机接收到的信号一般可以描述为如下形式［1］：（1）式表示Ns个可视卫星信号的总和，由Ns个不同的卫星发射。其中，ηRF（t）表示噪声；t为连续时间变量。

接收机天线接收到的第i个卫星发射的信号结构如下：

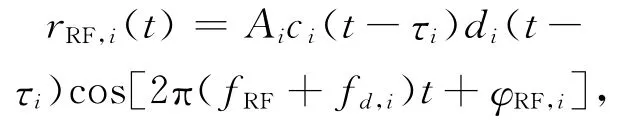
其中，Ai为第i颗可视GPS卫星信号的幅度；τi为传输通道引入的码相位延迟；ci（t－τt）为扩频码序列，其值为｛－1，1｝；di（t－τt）为导航电文，采用二进制移相键控调制方式，其中包含了卫星的轨道数据、定位数据、时间数据等信息；fd，i为第i颗可视卫星信号的多普勒频移；φRF，i为载波的初始相位偏移量；fRF为载波频率。

输入信号yRF（t）由接收机天线接收，再经过射频前端下变频和滤波，即得到下列表达式：

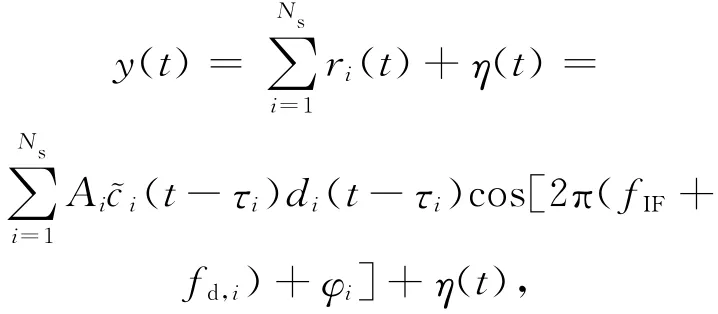
其中，fIF为接收机中频频率；～ci（t－τi）为射频前端滤波后的扩频码序列，此处可以取近似（假设射频前端滤波器的影响可以忽略）：～ci（t）≈ci（t）；η（t）为射频前端下变频和滤波后的噪声分量。

在数字接收机中，信号y（t）经过模数转换器（analog－to－digital converter，ADC）采样之后得到数字中频信号IF，ADC以采样频率fs＝1／Ts对y（t）进行采样后得到采样序列y［nTs］，记x［n］＝y［nTs］，则有：

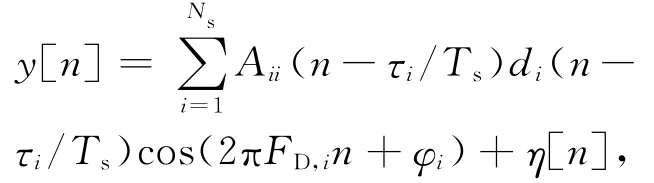
其中，FD，i＝（fIF＋fd，i）Ts。

离散时间随机序列η［n］的扩频特性由射频前端的滤波器类型、采样抽取策略等决定。如果使用的采样频率为fs＝2BIF＝4fIF，那么中频信号和噪声的采样将会按照奈奎斯特采样率进行，其中BIF是射频前端的带宽。在这种情况下，有

另一个重要参数是噪声的自相关函数：

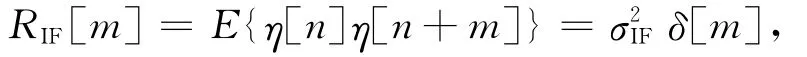
其中，η［n］为典型的独立同分布宽平稳随机过程；δ［m］为克罗内克δ函数；m、n为离散时间变量。

利用扩频码的正交特性，GPS接收机可以区分不同的GPS信号，只处理其中某一个GPS卫星信号，去掉下标i后，得到信号的表达式如下：

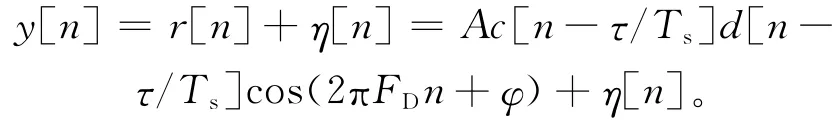
2 捕获策略

一般情况，当GPS接收机成功捕获到可见卫星信号，相应地接收通道就应该从捕获阶段进行到跟踪阶段，然而，当跟踪阶段的锁定环路判定信号失锁后，接收通道即从跟踪阶段返回捕获阶段。

一般 GPS接收机通道有几个状态［2－3］，在任意时刻，接收机通道都会处于如下某一状态：等待、捕获、确认牵入和跟踪。接收机在捕获到信号后，依次进入确认和牵入状态后再进入跟踪状态，从而提高接收机信号捕获的可靠性和信号参数估计的精确性。

待机状态，即接收机通道处于闲置时的状态，此时接收机不执行任何操作，而是等待卫星信号变成可见状态或者等待有效信号的输入。

捕获状态即指接收机在检测到某卫星信号可见后对可见卫星信号进行二维搜索的过程。

在确认状态，接收机停止在其余各个搜索单元上的信号搜索，而是在检测到信号的搜索单元上进行搜索，进一步确认该搜索单元是否确实存在可见卫星信号。

当接收机成功地确认某颗卫星信号存在时，就可以对捕获得到的码相位和多普勒频移值进行优化，减小其误差，从而得到更精细的估计值。

各状态之间的转换如图1所示。

图1 接收机通道状态转换图

3 实 现

接收机启动之后，根据设置的初始化参数值对各信号参数进行初始化。

在捕获阶段，采用并行码相位搜索捕获算法［4］对GPS信号进行快速捕获，这样码相位搜索通过傅里叶变换一次就能完成，从而使捕获次数由线性搜索捕获法的次数急剧地减少到只在频率一维内的搜索次数，这大大提高了搜索捕获效率，节省了搜索时间。在确认阶段，采用N取M搜索检测器［5］的固定时间段检测器，N取M搜索算法如图2所示。

图2 N取M搜索检测器算法

图2中，J表示比较中取样值V大于门限值Vt的次数；K表示最大取样次数；M表示确定信号存在的J的最小值。

N次试验的总虚警概率［6］为：

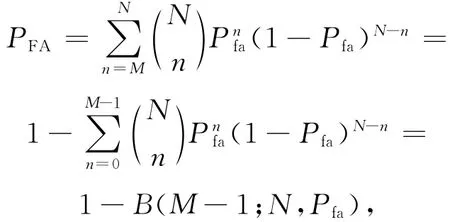
其中，B（M－1；N，Pfa）为累积概率密度函数；Pfa为单次实验的虚警概率。

N取M搜索检测器对于每个方格取N个包络，并将其与门限做比较。如果其中有M个或M个以上包络值超过门限值，则认为信号存在。否则认为信号不存在，并且开始下一个搜索方格的搜索，重复上述操作。N取M算法包含比较好的基准噪声源技术。选取合适的M和N值，可以提高捕获的可靠性，减小虚警率。

为了减少所要执行的相关运算的总数，降低捕获所用的时间，捕获阶段采用的搜索空间中的2个相邻搜索单元之间的距离比较大，然而，过于粗略的码延迟和多普勒频移估计值会引起跟踪的不正常运行，比如频率锁定环路或延迟锁定环路可能无法锁定输入信号。

要提高捕获的准确性，需要对数据进行优化，采用线性搜索方式［7］进行处理。

（1）在频域执行优化。固定码相位延迟，改变多普勒频移，然后分别作相关计算，通过比较最后的相关结果来判断最佳的多普勒频移估计值。

（2）在码相位域进行优化。固定多普勒频移值（上一步中的优化结果），依次改变码相位值，再次作相关运算并比较相关结果，从中找到最佳的码相位估计值。

在对多普勒频移估计值和码相位延迟估计值做优化时，一般利用确认阶段的结果，对确认存在的GPS卫星信号作相关的处理，不存在的信号即可忽略，这样可以节省时间，在一定程度上保证时间效率问题。

整个优化阶段结束后，即进入信号跟踪阶段。

4 仿真与实现

为了验证捕获策略的正确性和可行性，对接收机的信号捕获能力进行仿真分析。仿真采用的数据［8］是由射频前端采集的真实数据，其中GPS中频信号的采样频率为38.192MHz，中频频率为9.548MHz。

图3所示为接收机捕获阶段的捕获结果，从图3中可以明显看出，15、21、22号等卫星信号的可见性特别好。

图3 GPS卫星信号捕获结果

表1所列为并行码相位搜索算法捕获到的卫星信号的多普勒频移和码相位的估计值。

依据制定的捕获策略，在粗捕获完成之后，需要使用N－M搜索检测算法对初捕获中的结果进行确认，以确保接收机搜索捕获结果的可靠性，减少随机性。

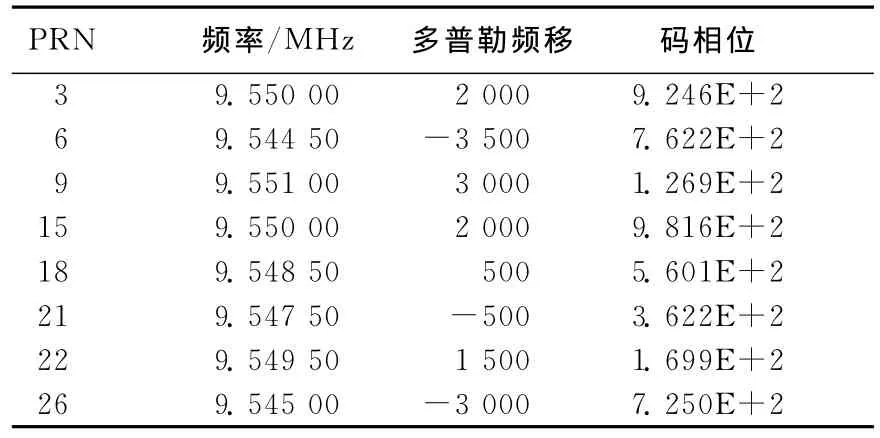
表1 GPS卫星信号初捕获结果

经确认，上述捕获的GPS卫星信号中PRN为6、15、18、21、22、26的卫星信号确实存在，因此进入下一步优化阶段。这样可以省去对虚假信号的相关运算，缩短捕获时间，提高效率。若省去确认阶段，则需要对初捕获阶段的所有结果进行处理，会带来不必要的时间消耗。优化分为对频率进行优化和对码相位估计值进行优化2个部分。

首先采用串行搜索捕获算法对码相位值进行优化，其结果见表2所列。

表2 码相位估计值的优化结果

码相位优化结束后，再对多普勒频移进行优化，结果见表3所列。

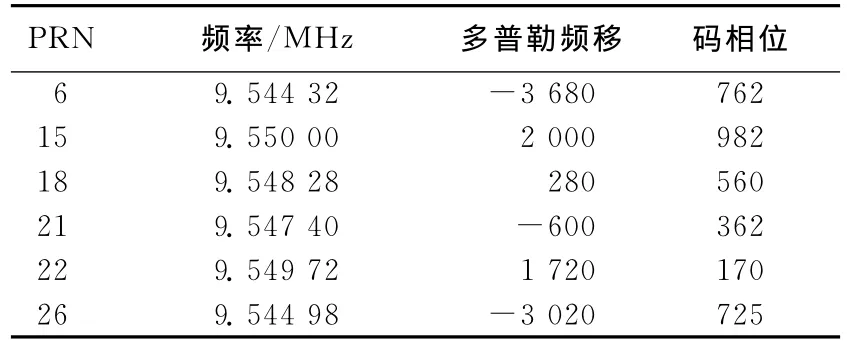
表3 多普勒频移估计值的优化结果

在完成所有操作之后，得到的最终结果（表3所列中的数据）就可以作为捕获的最终结果而转入跟踪阶段。

可以绘制单个卫星信号的捕获结果图，直观地观察捕获情况，如图4所示。

图4 PRN＝21的卫星信号捕获结果

同样，也可以分别绘制多普勒频率和C／A码相位的捕获结果，如图5所示。

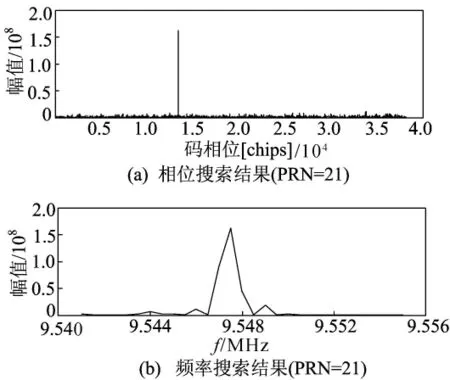
图5 PRN＝21的频率与相位捕获结果

5 结束语

本文在常用GPS捕获算法的基础上，提出了一种适合GPS软件接收机的搜索捕获策略，这种策略简单高效，容易实现。其中，把信号由时域变到频率进行处理，能大大减少相关性计算的运算量。使用N－M算法可以保证信号搜索结果的可靠性。最后的优化阶段在时间效率允许的情况下，采用更小的搜索步长，可以得到更加精确的捕获结果，这样也对跟踪阶段做了很好的铺垫。

［1］ Sun K，Presti L L.A differential post detection technique for two steps GNSS signal acquisition algorithm［C］／／Position Location and Navigation Symposium （PLANS），2010 IEEE／ION，IEEE，2010：752－764.

［2］ 陈 慧，徐定杰，袁瑞铭，等.基于FFT的并行捕获的研究［J］.弹箭与制导学报，2003，23（5）：28－31.

［3］ Kelley C，Barnes J，Cheng J.Opensource GPS open source software for learning about GPS［C］／／ION GPS 2002，2002：2524－2533.

［4］ 谢 钢.GPS原理与接收机设计［M］.北京：电子工业出版社，2008：372－374.

［5］ 长普兰.GPS原理与应用［M］.寇艳红，译.北京：电子工业出版社，2007：162－170.

［6］ Ward P W.GPS reciver search techniques［C］／／Position Location and Navigation Symposium，IEEE，1996：604－611.

［7］ 张 勇，林宝军，徐志瀚.软件GPS接收机信号搜索捕获的仿真 实 验 研 究 ［J］.系 统 仿 真 学 报，2006，18（9）：2646－2649.

［8］ 杨东凯，张飞舟，张 波.软件定义的GPS和伽利略接收机［M］.北京：国防工业出版社，2009：50－150.