路Pn的补图Pn的可扩性研究

王锦伟 （ 兰州工业学院基础学科部 730050）

路Pn的补图Pn的可扩性研究

王锦伟 （ 兰州工业学院基础学科部 730050）

在连通图中任取n条点不交的边，如果这些边可以扩充成的一个完美匹配，就称连通图是n-可扩的。本文中我们主要研究偶长路P2n的补图的1-可扩性以及奇长路 的补图的-可扩性。

路 补图 完美匹配 可扩性

一、引言

笔者仅讨论有限、无向、简单图，所使用的记号和术语约定如下。其中未说明的部分请参考文献。

二、主要结果

为了证明方便，我们对路Pn的补图的顶点集边集

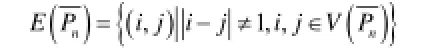
（如下图）。

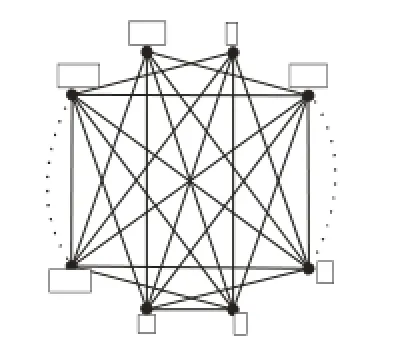
首先我们考虑偶长路P2n的补图的可扩性。

定理1.偶长路P2n的补图的1-可扩的。

情形1.k和k的奇偶性相同。

不妨假设k和k都是奇数且有k＜i。于是C=ij（ j+2）...（2n-1） 13...（i-2）（i+2）...（j-2） 24...（2n）是的一条Hamilton路，因此存在包含（）,i j的完美匹配。

情形2.k和k的奇偶性不同。

不妨假设k是奇数，k是偶数且k＜i，于是C=ij（ j+2）...（2n）24...（i-1）（i+1）...（j-2） 13...（i-2）（i+2）...(2n -1)是的一条Hamilton路，因此存在包含（i, j）的完美匹配。

综上可得偶长路P2n的补图的1-可扩的。

接下来我们考虑奇长路P2n+1的补图的可扩性。

定理2.奇长路P2n+1的补图是-可扩的。

情形1.,,i j k的奇偶性相同。

情形2.k和k的奇偶性相同，与k的奇偶性不同。

情形3.k和k的奇偶性不同。

不妨假设k是奇数，k是偶数且有ki＜。而k与k或k的奇偶性相同，不妨假设k是偶数。

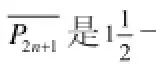
[1]徐俊明.图论及其应用（第二版）.中国科学技术大学出版社，2005.

[2]M.D.Plummer， On n-extendable graphs，Discrete Math. 31（1980）201-210.

[3]Q.Yu，Characterizations of various matching extensions in gaphs，Australas. J.Combin.7（1993） 55-64.

（责编 齐 真）